基于模拟退火算法下多位相型达曼光栅分束器的设计

史 发，蔡荣立

(西安工业大学 光电工程学院，西安 710021)

0 引言

Dammann(达曼)光栅[1]是一种具有特殊孔径函数的衍射结构，可以用于在夫琅禾费衍射下产生均匀点阵或线阵的结构光的衍射元器件。对其的应用也非常广泛，在三维测量中，相比于传统投影结构光，具有衍射效率高、均匀性高与结构光参数易控制等优点[2]，是目前最有效的分束器件，因此受到了广泛学者们的认可。

针对光栅的应用需求，多数学者们对其进行了更深一步的研究，如最早上海光机所[3]研制出64×64点阵的达曼光栅，J.Jia课题组与周常河课题组[4-7]，对其的设计优化、加工制作与应用都展开了更详细的说明。从现有研究结果中发现，多数研究都是基于光栅的突变点坐标，利用模拟退火算法对其进行不断的优化[8-9]，设计出来的结果都是二值振幅型或二值位相型，缺少对每个结构的相位值进行优化设计，优化设计后对于衍射型光栅来说，衍射效率会更高。

针对上述问题，提出了一种基于模拟退火算法下多位相型达曼光栅分束器的设计方法。在传统二值振幅型达曼光栅的基础上，将其作为初始结构，采用模拟退火算法对相位结构进行离散、调制后，通过控制评价函数来对最优的设计结果进行评判。为了验证所提算法的有效性，通过软件对9×9点阵的Dammann光栅的相位结构进行仿真分析，最后对所计算出来的相位结构进行实验验证测试。结果表明，与传统的Dammann光栅设计方法相比，所提方法具有优越性与有效性，为实际应用中三维测量结构光的产生提供了理论基础。

1 系统结构及原理

1.1 传统Dammann光栅设计理论

Dammann光栅是一种具有特殊周期结构的分束型衍射光栅。一般情况下光栅的相位值为二值(其值大小为0或π)[10]，研究计算时对光栅的结构都进行周期归一化处理。因此在理论分析与结构设计的过程中都是只研究Dammann光栅的一个周期，如图1所示，为了更直观的表示出一维Dammann光栅的结构，通过对一个周期内的突变点坐标进行归一化处理得到如图1(a)所示的一维Dammann光栅的一个周期内坐标示意图，然而，二维Dammann光栅的结构很简单，即是对两个一维Dammann光栅进行正交合成，即可成为一个位相型Dammann光栅结构，如图1(b)所示，图中白色表示透光部分(具体对应的相位值为0)，黑色表示不透光部分(具体对应的相位值为π)，对于二值而言，在合成的过程中应注意正交叠加合成保持二值不变。

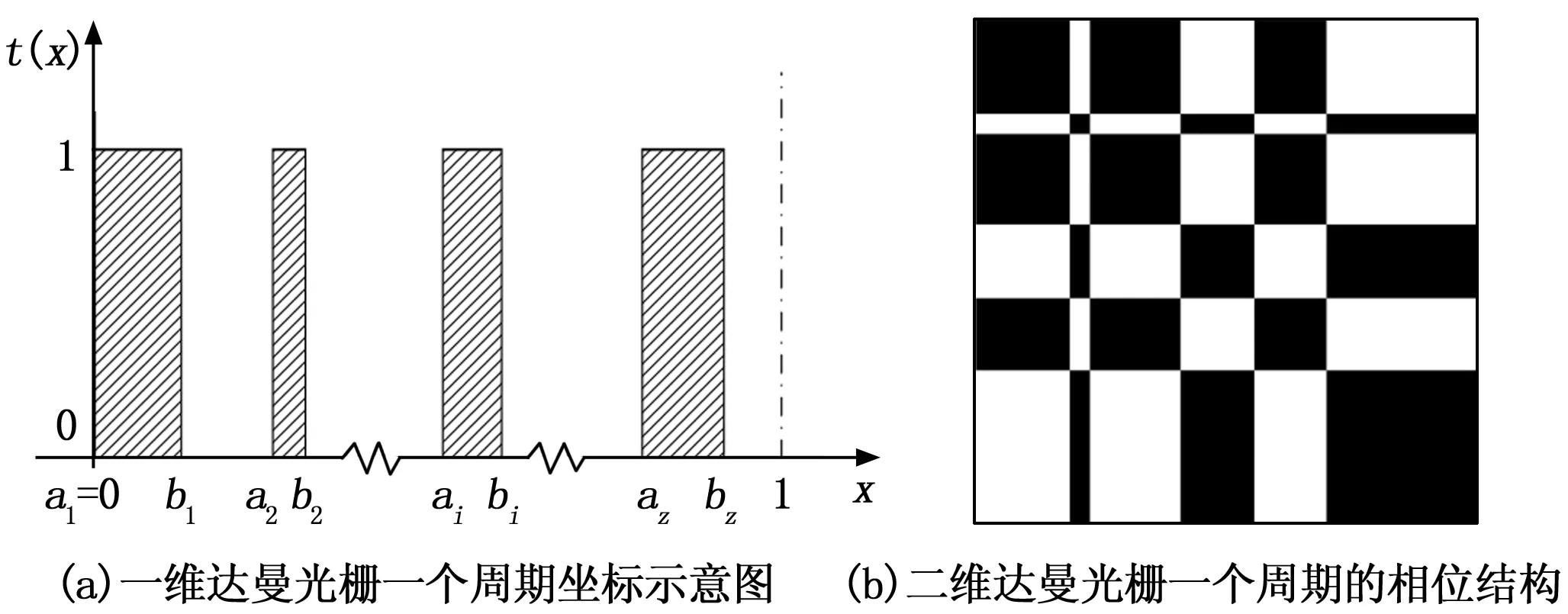
图1 达曼光栅相位结构示意图

Dammann光栅与其频谱的分布是完全由设计时光栅结构中所有突变点坐标{aZ，bZ}决定。因为其透过率函数tb(x)具有规律分布的周期性，因此对其进行傅里叶级数展开，展开的结果为：

(1)

式(1)中：n表示对应结果中的不同衍射级次；其每个级次所对应的傅里叶级数为：

(2)

为了提高Dammann光栅的衍射效率，将相位值θφ引入，为了计算方便，用突变点坐标表示光栅的傅里叶系数，其所对应的频谱函数为：

TG(n)=2Tb(n)sinθφ

(3)

所对应的功率谱即为频谱的模的平方，因此光栅的各级功率谱为：

G(n)=|TG(n)|2n=-∞，···，∞

(4)

G(0)=G(±1)=···=G(±N-1)=G(±N)

(5)

在上述理论表达式分析完之后，算法为了评价优化结果，要用评价函数对其进行控制，因此定义误差函数为：

+(1-β)(1-GE)2

(6)

前面所说的计算过程中的目标评价函数、突变点坐标{aZ，bZ}与相位角θφ之间是一个十分复杂的关系，不能用具体的数学模型表达式进行表示，因此才需要采用相关优化算法进行优化无限的逼近，即本文所研究的模拟退火算法。

在优化设计的过程中，温度的大小与降温过程会对结果的好坏产生一定的影响，因此所选取的降温公式为：

(7)

式(7)中参数χ=0.97。初始温度t0=1 000。

根据上述计算公式，采用模拟退火算法进行不断优化设计，可以得到最终的突变点坐标集合，即可得到上述光栅的最终结构。设计结果的突变点坐标如表1所示。

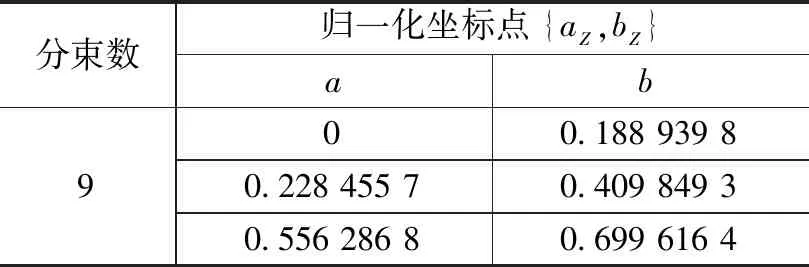
表1 突变点坐标设计结果

对于上述突变点坐标，因为是归一化的设计结果，所有突变点值的范围是在0～1之间，是相对于一个光栅周期的，具体周期的大小可以根据设计需求确定，由传统的光栅衍射方程式(8)可知：

dsinθ=mλ

(8)

式(8)中d为光栅的周期，λ为入射光波波长，m=0，±1，±2···，θ为光栅的衍射角，因此周期决定着衍射角，与衍射角呈反比关系。然而，对于达曼光栅分束而言，衍射角决定着输出点阵点与点之间的间距，衍射角越大间距越小，衍射角越小间距越大，衍射角与点阵间距呈现反比关系，即光栅周期d与点阵中点与点之间的间距呈反比关系。

1.2 改进Dammann光栅设计思路

根据上述理论基础，在一个二值振幅光栅的基础上，对一个周期内的相位结构先进行离散，再进行调制。具体离散、调制方法是对选取一个周期的相位结构，采用等间隔分割，分割完后，在分割后的每个小单元的基础上对其相位值进行改变，改变顺序为从下往上、从右往左，离散、调制示意图如图2所示。

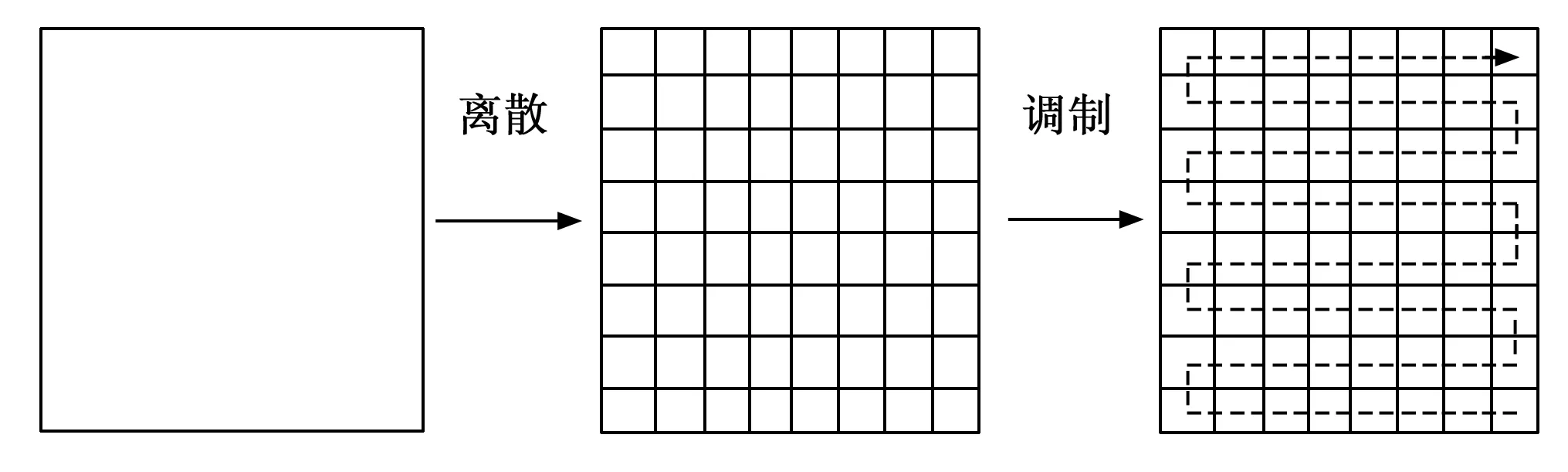
图2 优化设计中离散、调制示意图

在离散的时候，应注意离散过程中是等间隔离散，显然易知，离散点越多，设计的结果肯定会越好，并且会伴随着运算量的增大；离散点越少，设计的结果性能会有所降低，但是运算时间会减少，因为模拟退火算法相对于其他算法是一个比较耗时的迭代算法，但该算法的优点是不会陷入局部最优，而是会得到全局最优的结果。因此设计过程中必须考虑到现实加工要求，一个周期的大小与离散点数之比，就是最终光栅的最小特征尺寸，为了设计的结果质量高、加工容易，周期与离散点的选取要有一定的范围。

在调制的过程中，是对离散后的每个采样点按照从右到左、从下往上的顺序依次调制，也就是利用模拟退火算法进行波动取优。调制过程主要决定了运算速度，因为每一次对每个采样点进行一次波动都是对模拟退火算法的重复运行。因此所采用的离散与调制在很大程度上面的决定了该算法迭代寻优的计算能力。合理的参数设置，对结果的改进具有很大的意义。

采用模拟退火算法对相位结构进行优化时，算法中最重要的有两个控制条件需要得到合理准确的设置，随机扰动和目标函数。随机扰动是对光栅的相位值进行改变，因为它每次的变化大小会对评价函数有影响，决定着对变化之后结果的取舍。由于设计的Dammann光栅相位结构中，每个小单元的相位值在-π～π之间，所以设置随机扰动的范围在相位最大范围的1%～3%之间即可。因为设置的过大，很难找到最优解，主要原因是在相位值波动的过程中，某个小单元的值变化之后会对分束结果的质量产生很大质的变化，波动之后，算法始终在寻优中不断徘徊；若设置过小，算法的运算周期会增加，主要原因是每次对每个小单元的相位值进行波动之后，变化量太小，以至于对分束结果的质量影响变化很小，在目标函数的取舍过程中会浪费时间，降低迭代寻优的效率。因此波动范围的设置也是通过不断仿真计算实验得到的结果。目标函数定义为衍射效率和光强不均匀性如式(10)和(11)所示，将其加权后作为目标函数，当目标函数中衍射效率和光强不均匀性同时满足时，接受其波动后新的相位结构，若有一个不成立，则采用Metropolis[11]准则确定是否接受。

Metropolis准则为：

(9)

式(9)中：k为玻耳兹曼常数；T为绝对温度；P(ΔE)为小于1的数。用随机函数产生一个[0，1)区间内的数，与P(ΔE)进行比较，如果P(ΔE)>随机数，则接收新解，如果小于，则舍去。

Metropolis准则运用在该算法中的具体计算公式为：

(10)

式(10)中：Tk+1为在温度为T时，迭代次数为k+1时的状态，fk+1、fk分别为第k+1与第k次Dammann光栅分束结果所对应的评价函数。

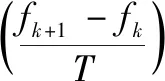
设计时采用衍射效率、光强不均匀性与均方根误差来衡量最终设计结果的好坏，定义的具体计算公式[12]如式(11)所示。

定义衍射效率η为输出平面所需目标区域内N×N个点总光强与输出平面目标区域内内所有总光强之比，即：

(11)

式(11)中，Imn为输出平面目标区域内所有点的光强；Ikl为输出平面目标区域内N×N个点中第(k，l)个像素点的光强。目标区域是输出面区域的N×N分布的点阵方形范围。

定义光强不均匀性rms为输出平面所需目标区域内各点的最大光强与最小光强之差和最大光强与最小光强之和的比，即：

(12)

式(12)中，Imax、Imin分别为输出平面所需目标区域内各点的最大光强与最小光强。

定义均方根误差为输出结果与理想结果的差异，具体计算公式为：

(13)

式(13)中：I、II分别为实际输出结果与理想输出结果，mn为输出面采样点数。

具体运用模拟退火算法的计算流程如图3所示，将初始条件设置为二值振幅光栅的相位结构，在其基础上对相位结构进行扰动，目标函数为上述衍射效率和光强不均匀性的加权表达式，具体为式(14)所示。

图3 模拟退火算法流程图

f=aη+brms

(14)

式(14)中，f为加权后的评价函数，a、b为控制系数，与上述式(6)中α一致，作用就是分别控制光能利用率与光强不均匀性在设计中的不同占比。一般情况下，对光强不均匀性的要求会更高一点，因为光强不均匀性与光能利用率是两者很难兼得的结果，光能利用率高的话，光强不均匀性就会高，反之一样。但是一般会在光能利用率可接受的范围内，尽可能的提高光强均匀性，主要是光强不均匀性对分束结果的质量影响很大，即便是光能利用率低，想提高分束结果的能量可增加入射光的能量大小，但是如果结果中光强分布不均匀的话，质量会有所降低，是很难控制其他条件来对其进行改变的。因此上述系数中b相对于a可能会在值上有较大的差异。

根据上述控制条件进行具体参数的设置，利用模拟退火算法进行优化设计，即可求出Dammann光栅的最优相位结构。

模拟退火算法的计算流程为：

1)首先设置初始参数，如初始温度、迭代次数、评价函数、退火函数、初始解、波动范围等。

2)计算出初始解所对应评价函数的值，然后根据上述思路(离散、调制)对初始解中每个像素点的相位值进行相应次数的随机波动。(波动过程中要注意取舍，每个像素点的相位值不能超过-π～π这个范围)

3)然后计算波动之后的评价函数，与上一次的评价函数进行比较，若波动之后的解比上一次的解更优，即符合要求，对其接受，将其作为当前状态下的最优解，若不符合要求，则按照Metropolis准则进行取舍。

4)按照上述的设计思路对每个像素点的相位结构都以此重复波动，直到将一个光栅周期内的每个像素点波动完之后，也就是达到迭代次数之后，计算最终的结果是否为最优的设计结果，若符合对其进行输出，算法停止，得到最优的设计结果，若不符合则通过退火公式进行一次降温。

5)按照上述步骤继续开始下一轮的波动迭代计算，直至达到最优条件，或者达到设置的最终计算条件，输出最优解。

2 仿真分析

以9×9分束为例，一个光栅的周期大小设为0.375 mm×0.375 mm。将一个周期内离散为30×30个小单元。每个小单元的大小为0.012 5 mm×0.012 5 mm，光栅结构尺寸为15 mm×15 mm。初始结构中对应的一维Dammann光栅归一化相位突变点坐标为0.188 939 8，0.228 455 7，0.409 849 3，0.556 286 8和0.699 616 4，将其进行正交合成，合成为二维二值振幅光栅，具体的结构如图4(a)所示。通过算法优化，将迭代最大次数设置为10 000次，每次温度下的迭代次数为1 000，在迭代次数下，刚好对一个周期内的所有采样点进行一次算法上的波动取优，最高温度为1 000 ℃，降温公式采用为下式(15)所示：

图4 传统二值振幅型设计结果

T(k+1)=α·T(k)

(15)

式(15)中：k为迭代次数，α为降温系数，一般取0.98。降温公式决定着每一次计算过程中的迭代温度，温度主要取决于Metropolis准则对波动解的取舍情况，它对最优解的选取有着直接的决定关系，因此合理的降温公式对最优结果的寻找由很大的帮助作用，不仅可以提高计算速度，还可以提高最优结果。

经过模拟退火算法设计后，得到达曼光栅的衍射效率为85.3%、光强不均匀性为0.095 2%、均方根误差为8.2×10-5的设计结果，如图5所示。

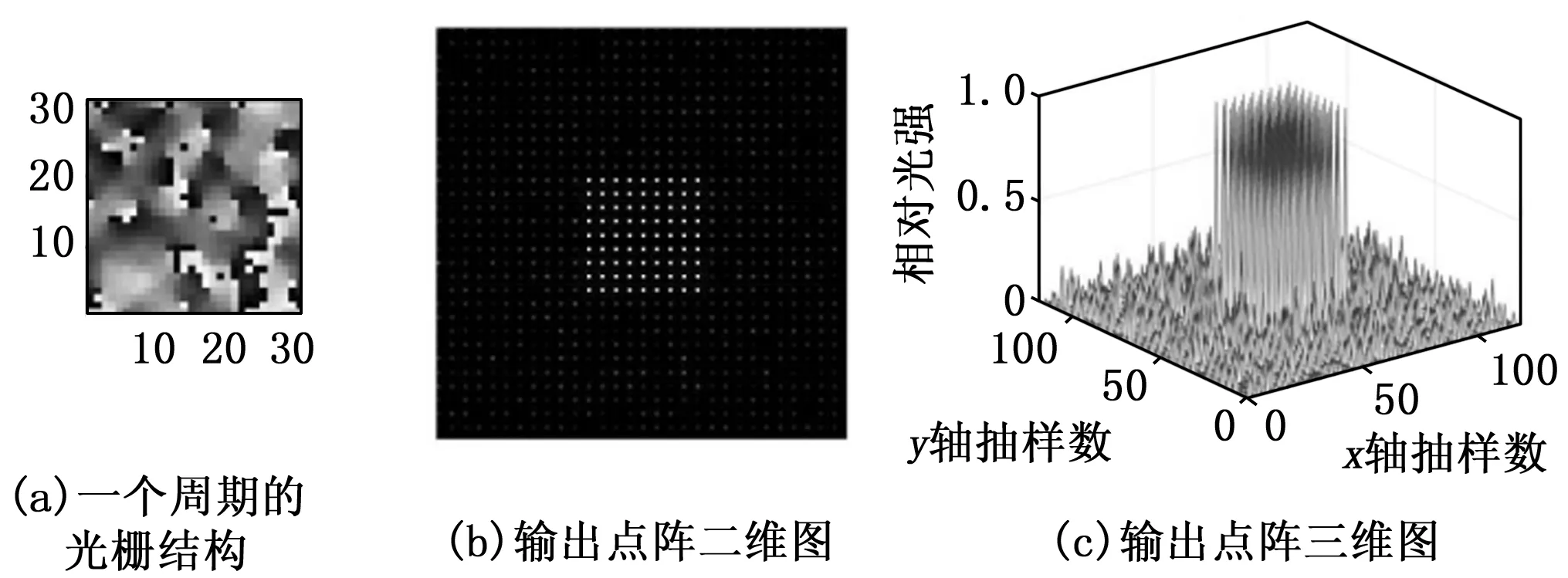
图5 模拟退火算法后的达曼光栅设计结果

图4与图5分别为传统二值振幅型达曼光栅与经过模拟退火算法后的达曼光栅的设计结果，包括一个周期内的相位结构与分束结果的二维、三维示意图。经过图4图5对比可以看出来，二值振幅型达曼光栅的分束结果中，9×9点阵所对应的81个点的光能值差异很大，能量分布服从sinc函数分布，亮暗不均匀，即光强均匀性很低，并且旁边还有其他高级次的点，对光能利用率有很大的影响，但是从经过模拟退火算法后的达曼光栅设计结果来看，结果中81个点的光能值非常均匀，其之间的能量相差小于10-4个数量级，因此光强均匀性是非常好的，相对于传统二值结果而言，虽然旁边还会有其他级次的点，但是相对于需要的81个点的光强值的很小的，具有很高的光能利用率。

上述设计结果中，传统二值型达曼光栅的衍射效率为68.43%，光强不均匀性为34.53%，而改进之后的设计结果，衍射效率为85.3%、光强不均匀性为0.095 2%，相对于之前，衍射效率提高了20%，均匀性提高了34%，得到很好的设计结果。可以看出传统突变点坐标下的达曼光栅，分束结果中，光栅的衍射效率很低，并且均匀性很弱，虽然加工容易方便将两个一维光栅正交合成即可，但是结果的性能不高，特别是每个点之间的光强均匀性，然而，改进之后的算法设计结果中，衍射效率得到了提高，并且均匀性也得到了提高，对分束结果的质量有很大的帮助。

在计算的过程中，通过观察衍射效率与光强不均匀性随计算时间的变化，得到其变化曲线图如图6所示，可以看出，起初阶段衍射效率是在降低，不均匀性是在增大，是因为起初选取的温度与随机波动的变化量相对于所设置的初始解可能与之不匹配，导致算法不但没有再找最优解而是在破坏所选取的初始解，但是当计算过程中经过某一阈值后，发生了变化，算法开始步入寻找最优解的道路上，计算效率迅速提高，衍射效率逐渐增大，不均匀性逐渐降低，直到达到最优结果，或计算结果趋于某一定值，因为经过一定时间的变化后，当前温度、当前结构、随机波动的大小三者重要因素相匹配，算法开始寻优。从计算结果看出最终所用计算时间为4.6个小时。

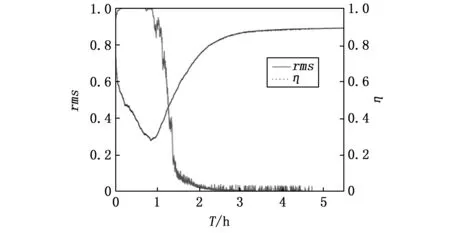
图6 衍射效率与不均匀性随计算时间变化曲线图

3 实验验证与误差分析

根据设计的结果，对其进行实验验证，一般采用加工制作，制作方法常称为图形转移技术。主要有“加法”与“减法”制作工艺，也就是所谓的刻蚀法[13-14]与沉积法[15-16]。但是为了验证实验结果，为例减小成本与更方便采用液晶空间光调制器代替加工好的达曼光栅进行实验验证。液晶空间光调制器(LC-SLM)[17-21]的工作原理是利用液晶分子所具有的双折射性，在外加电压控制之下，通过电压控制改变不同像元内液晶分子的偏转来改变液晶材料的折射率，可实现对入射光的调制。最终通过CCD进行采集实验结果。实验光路如图7所示。

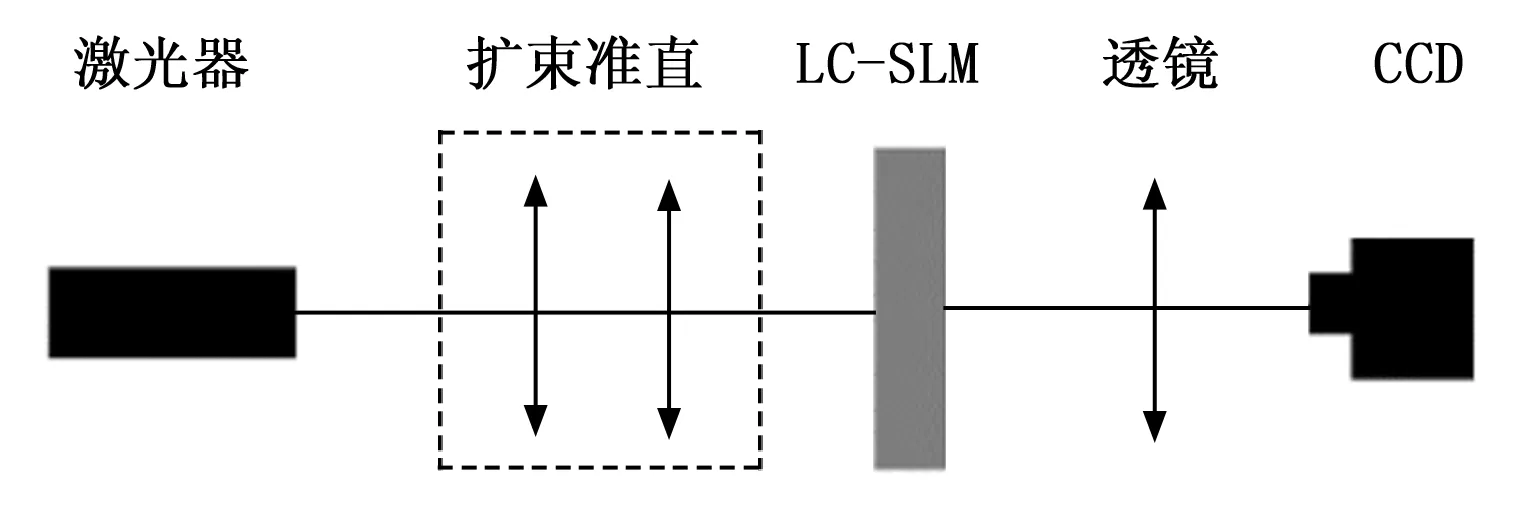
图7 产生结构光实验光路图

图7中采用波长为632.8 nm的氦氖激光器作为实验光源，再经过扩束准直系统，通过液晶空间光调制器，再通过透镜将衍射像成在焦平面上，最后用CCD相机进行接收实验结果。搭建好产生结构光的光路后，通过相关软件将设计好的达曼光栅的相位结构加载到液晶空间光调制器上，调节相机CCD在透镜焦平面处进行观察，并对结果进行采集。

将上述设计的光栅相位结构，进行实验观察，得到结果如图8所示，通过仿真与实验的对比，此方法设计的相位性光栅，分束效果得到了提高，结果中衍射效率高，均匀性高，对三维测量有很好的应用价值。

图8 实验结果9×9点阵光斑(局部放大图)

将实验得到的结果进行分析，得到9×9点阵光斑的归一化光强值为表2所示，测得到衍射效率达到73.5%、光强不均匀性达到10.0%、均方根误差达到0.255。

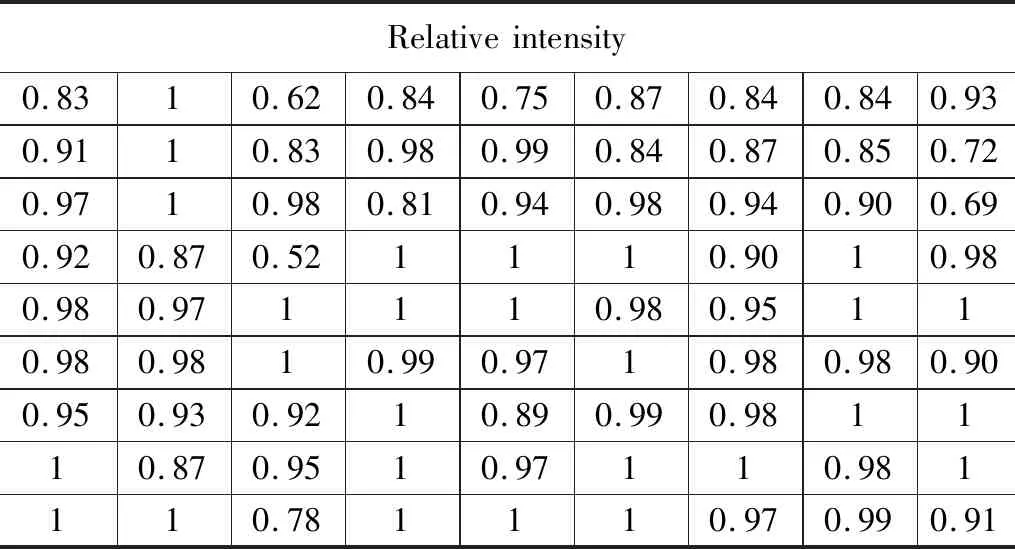
表2 设计9×9点阵光斑相对强度

由于实验是采用液晶空间光调制器代替达曼光栅进行实验，液晶空间光调制器是通过相位图的灰度信息控制电压的变化，然后通过电压控制液晶分子的变化，进而调制相位，因此就会存在灰度信息与相位信息的匹配问题，在起初使用的过程中需要对其进行校准，两者之间的差异会对结果的质量产生一定大小的影响。其次，液晶空间光调制器自身的“栅格效应”会产生多级衍射像与零级光斑，因此肯定会对输出结果的质量产生一定的影响，也就导致上述实验结果与模拟结果会存在一定的差异，但是实验结果在误差允许的范围内是可以接受的。

4 结束语

本文以相位型Dammann光栅结构作为结构光分束器件，根据传统二值光栅的结构，对光栅一个周期内的相位分布值进行优化，通过模拟退化算法对其进行离散、调制，来完成对光栅相位结构的优化设计。本文通过上述新的优化相位方法，计算得到理论上的衍射效率为85.3%、光强不均匀性为0.095 2%、均方根误差为8.2×10-5，且在任意点数的情况下都非常实用。最终对设计结果进行了实验验证测试，观察实验结果，得到光能均匀分布的9×9点阵光斑。测试得到衍射效率达到73.5%、光强不均匀性达到10.0%、均方根误差达到0.255。研究结果表明，本方法对分束为任意点数高质量结构光的生成有很大的实用价值，对三维结构光的测量提供了很大的帮助。