基于双种群蚁群算法的AGV路径规划研究

刘 睿，杨程伟，高长水，李晓东

(1.南京航空航天大学 机电学院，南京 210016；2.江阴市辉龙电热电器有限公司，江苏 无锡 214401)

0 引言

随着电商、新能源等新兴产业的崛起，大幅带动了仓储智能化的全面发展，为智能工厂的研发和应用注入了新的活力，AGV的路径规划是智能工厂领域的一个重要课题，是仓储应用的关键环节之一。在二维地图的尺度上，有大量算法已被证明可以用于路径规划，包括A*算法[1]、人工神经网络[2]、遗传算法[3]、麻雀搜索算法[4]、蚁群算法等。

蚁群算法具备良好的寻优能力和较强的鲁棒性，但也存在收敛慢，易陷入局部最优等缺陷，许多学者通过改进蚁群算法来提高算法的寻优能力。李开荣[5]提出了一种基于转弯角度约束的改进蚁群算法，减少了路径的转弯次数。王雷[6]提出参数自适应改变，以提高收敛速度和全局搜索能力。Luo等人[7]引入差异化的初始信息素，加快算法收敛速度，并对死锁路径的最后两步进行信息素惩罚，解决了死锁问题。Jianhua Liu[8]将蚁群算法与人工势场法结合起来，对搜索过程进行引导，有效提高了算法的收敛速度。李涛等人[9]提出了一种基于达尔文进化论的蚁群算法，提高了搜索效率并有效避免了死锁问题，杨立炜[10]通过在地图初始化阶段封锁U型陷阱的入口避免死锁。白建龙[11]等人在蚁群算法中引入负反馈机制，充分利用失败信息来指导蚂蚁的寻路过程。杨海清[12]将蚁群算法应用到了水下无人机的路径规划领域。XianWei Wang[13]设计了基于改进优化蚁群算法的智能停车系统。

近年来，一些学者对蚁群算法的架构组成展开了研究[14]，提出多种群优化算法。游晓明等人[15-18]引入博弈论等机制用于种群间交流。马飞宇[19]提出了具有自适应步长的异构双种群蚁群算法，通过差异化蚁群的相互协作提高蚁群算法的收敛速度和寻优能力。Lee[20]结合遗传算法，提出基于不同视野的异构蚁群算法。

结合以上改进策略，提出基于差异化步长的双种群蚁群算法，并重新设计了启发函数和信息素更新方法。为解决死锁问题，提出将符合条件的单元格视为障碍物的“填充陷阱”策略。通过在栅格地图上进行对比实验验证了改进策略的有效性，并通过ROS小车完成了在真实环境下的AGV自主导航任务，对算法的可行性进行了验证。

1 环境建模及运动描述

常用的环境建模方法包括拓扑法、栅格法等，拓扑法是将地图抽象为点和边的集合，将地图中的关键位置作为节点，将节点之间的路径视为边，适用于简洁工作环境。而栅格法是将环境离散化为栅格，通过定义栅格是否可通行描述环境信息，进而对复杂作业环境进行较精确的描述。以某公司的半导体加热管道生产车间为例，该车间工位紧凑，且不同区域位置关系不规律，如图1所示，因此采用栅格法对地图进行建模。

图1 某公司的半导体加热管道生产车间

网格单元通过二进制信息表示，以”0”表示可通行网格，以”1”表示障碍物网格。按从上到下、从左到右顺序，依次标记栅格序号1，2，…，i，序号为i的栅格对应栅格坐标中心(x，y)的关系式如式(1)所示。

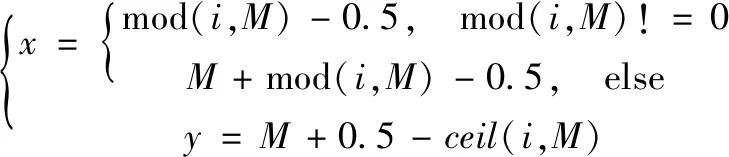
(1)

式中，mod表示求余运算，ceil表示向上取整运算，M表示栅格地图横轴最大值。图2是一个20*20栅格地图，其中黑色网格表示障碍物，白色栅格表示可通行区域，左上角栅格表示起点，右下角栅格表示终点。

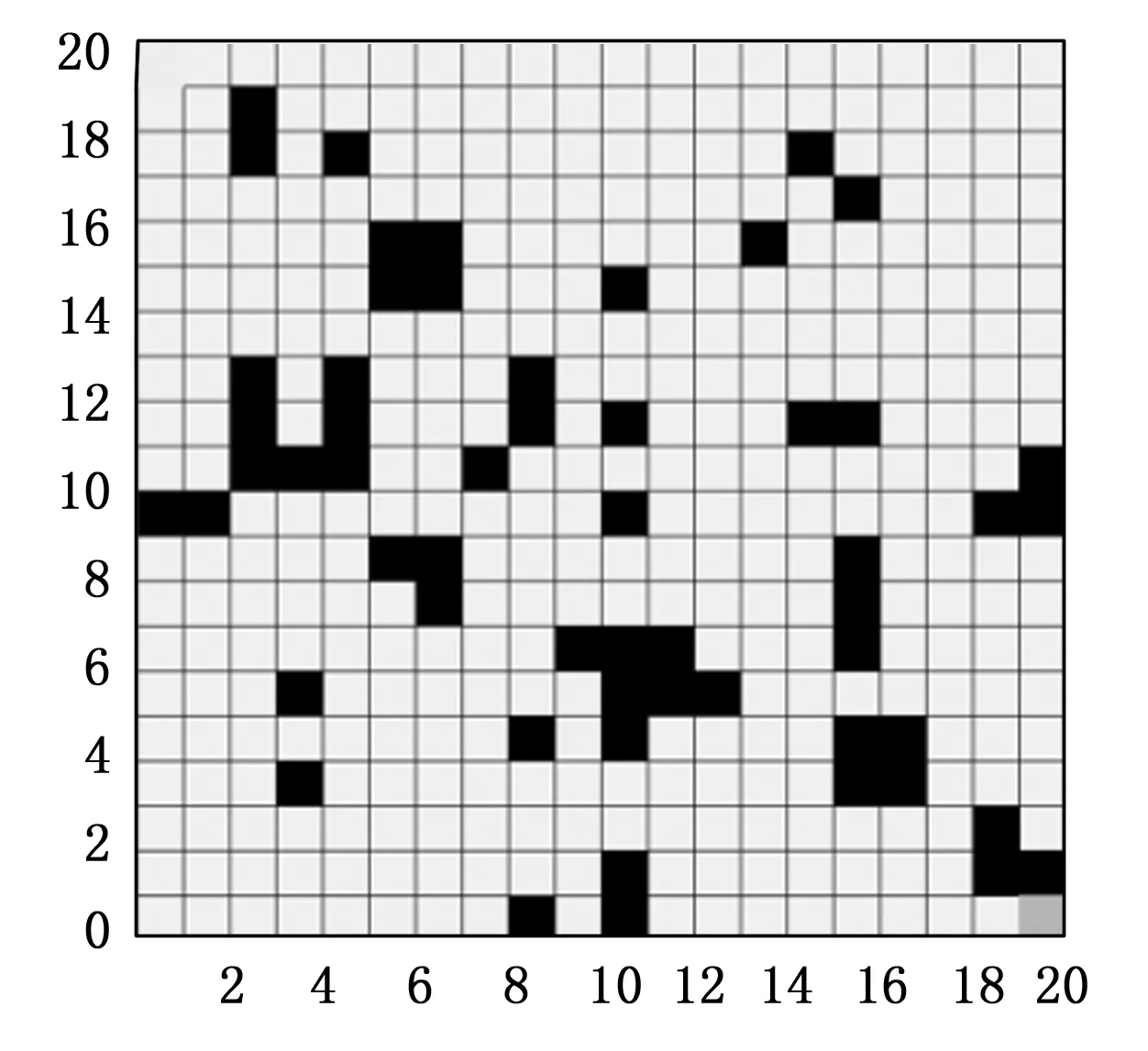
图2 栅格法环境模型图

定义AGV自身占据一个栅格，步长为1个栅格，其运动方向共八个方向，如图3所示。由于AGV沿45°方向运动时有可能碰撞相邻的障碍物，规定垂直于运动方向的相邻栅格均非障碍物时，才能斜向运动，即蚂蚁从栅格5直接移动至栅格10的充分条件是栅格9和栅格6是可通行栅格，否则只能沿如图4所示路线前进。

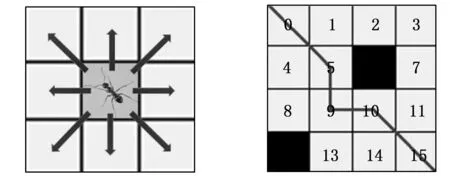
图3 AGV运动方向 图4 AGV防撞设定

由于AGV转弯时有时间损耗，单纯的路径长度不足以评定路径质量的好坏，因此以AGV在路径上的行驶时间代替AGV行驶距离作为路径优劣的评价函数，如式(2)所示。

(2)

其中：Ti是AGV沿第i只蚂蚁所寻路径行驶需要的时间，Li是第i只蚂蚁所寻路径的总长度，Ri是第i只蚂蚁所寻路径所转过的总角度，v是AGV的行驶速度，ω是AGV的转弯角速度，设AGV转90°所需时间等于其水平或竖直通过一个栅格的时间，AGV转45°所需的时间等于转90°所需时间的一半。

2 改进蚁群算法

2.1 信息素初始化

传统蚁群算法的信息素值在算法初始阶段是相同的，导致蚂蚁在迭代初期盲目搜索，在复杂环境中，这极大的增加了算法的搜索时间。因此提出一种基于节点位置关系和下一步可选择方向的数目的初始化信息素方法，设置不均匀分布的初始信息素，减少蚂蚁的盲目搜索，提高了算法早期的搜索速度，如式(3)所示：

τij(0)=Q×e((8-obs-1)-(dij+dsi+dje))

(3)

其中：Q是蚂蚁一次寻路可释放的总信息素浓度，obs是节点i周围8个节点中的障碍物数量，(8-obs-1)则是蚂蚁去除掉有障碍物的方向和来时经过的方向后下一步可供选择的方向数，dsi是起点至当前节点的欧氏距离，dij是当前节点至下一节点的欧氏距离，dje是下一节点至终点的欧氏距离。

2.2 状态转移公式

蚁群算法采用如式(4)所示的状态转移公式计算候选节点被选中的概率，并通过轮盘赌算法选择下一个节点。

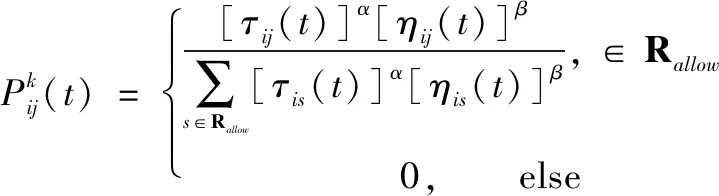
(4)

其中：Pijk(t)是节点j被选择的概率，[τij(t)]是节点i和节点j之间信息素浓度，α表示信息素启发因子，β表示期望启发因子，Rallow表示候选节点的集合，ηij(t)是节点i与节点j之间的启发函数值，传统蚁群算法的启发函数如式(5)所示。

(5)

由式(5)可知启发函数值与路径段的距离成反比，然而栅格地图中两相邻节点间的距离仅有1和两种情况，启发函数无法起到有效的导向作用，蚂蚁会倾向于选择距离为1的路径，造成传统蚁群算法搜索出的路径90°拐角过多，如图5所示。因此，引入候选节点的位置信息和AGV转弯角度，加强启发函数的引导能力，修改后的启发函数如式(6)所示。

图5 传统蚁群算法规划路线图

(6)

其中：c是常系数，γ是蚂蚁选择下一节点需要转的角度(rad)。

信息素启发因子α和期望启发因子β的大小会影响蚂蚁寻找路径的随机性，α过大或过小，都有可能陷入局部最优。β取值越大，蚂蚁越趋向于选择离目标点更近的局部最短路径。所以在算法初始阶段，先对α、β设置最小值，在算法初期增加全局搜索能力，并随迭代次数逐渐增大，α、β按式(7)、(8)从小到大更新，逐步提高算法的收敛性能。

(7)

(8)

其中：αmin、βmin分别为α、β的初始值，αmax、βmax是α、β的最大值，Nc为当前迭代次数，Nmax为最大迭代次数。

2.3 自适应步长

蚂蚁的视野指蚂蚁下一步搜索可选择的节点的集合，传统蚁群算法中蚂蚁的步长为1，视野仅局限于自身周围的八个节点，如图3所示，这种搜索方式造成算法收敛速度慢且易产生多余的拐点。扩大蚂蚁视野，使蚂蚁获得自适应步长，步长沿周围八个方向进行扩张，直到遭遇障碍物或抵达地图边界，而在沿斜向扩大步长时，还需考虑如图4所示的防撞设定，图6中透明阴影区域是蚂蚁获得自适应步长后的视野。

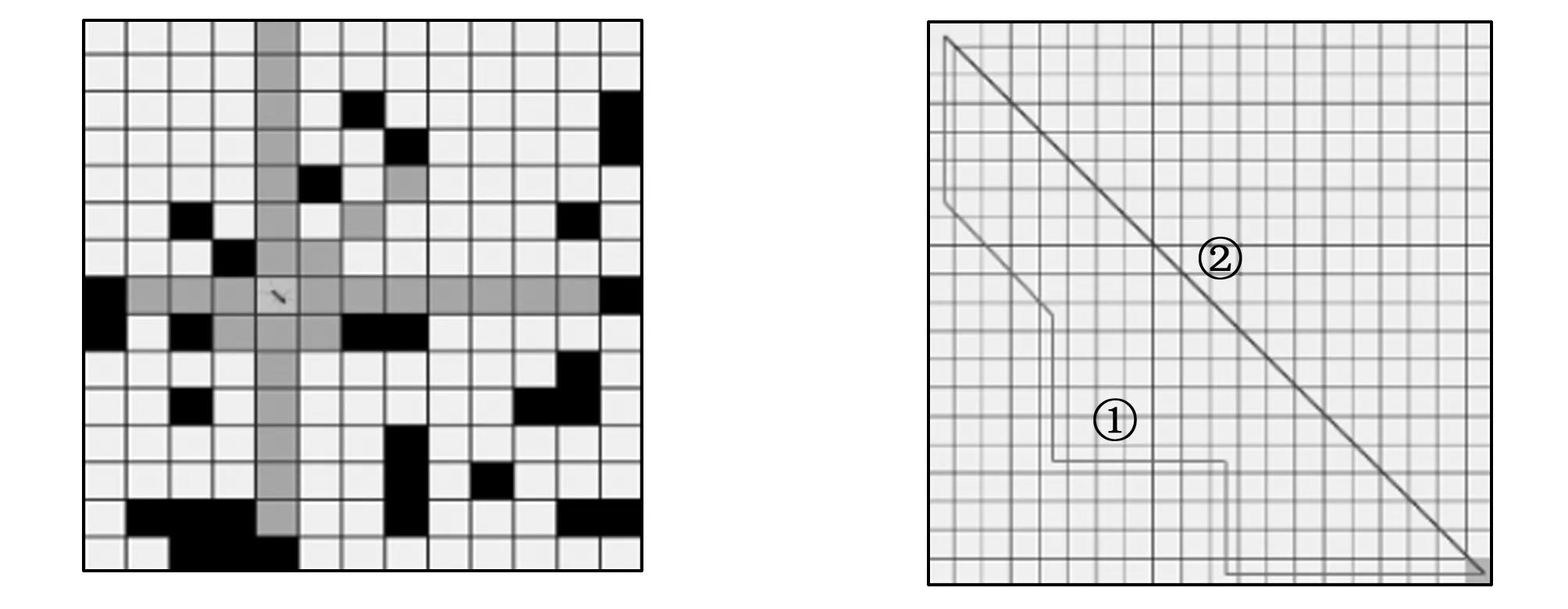
图6 自适应步长 图7 步长的影响

自适应步长策略可以减少路径中的冗余拐点，加快算法收敛速度，在如图7所示的地图中，需要规划一条从左上角至右下角的路径，传统蚁群算法从起点至终点的路径可能是路径①，而具备自适应步长的蚂蚁，可以在起点位置将终点位置纳入自身步长范围，从而选择路径②。

2.4 双种群蚁群算法

在单一算法中，提高收敛速度往往会降低搜索的多样性，反之亦然。由于蚁群算法本身具有良好的并行性，可以建立双种群蚁群算法，在传统蚁群算法的基础上引入了种群间的交流学习机制，让两个种群之间可以达到很好的优势互补，使算法性能得到了进一步提升，双种群蚁群算法研究的核心在于解的交流策略和信息素更新策略。

以2.1节至2.3节所阐述的改进策略为基础，建立以单步长改进蚁群算法为种群A，以多步长改进蚁群算法为种群B的双种群蚁群算法。其中种群A的搜索多样性较好，而种群B的收敛速度较快，使得算法可以在扩大搜索范围的同时兼顾收敛速度，种群结构如图8所示。

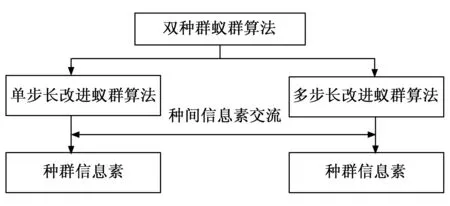
图8 双种群并行结构

在双种群蚁群算法中，种群间通过信息素交流来相互影响，不恰当的信息素交流策略会导致两种群都迅速陷入局部最优。因此建立基于种群间最优路径相似度的自适应信息素交流机制，提出种间竞争策略和种间合作策略，根据两种群最优路径之间的相似度选择合适的信息素交流策略。相似度通过式(9)进行判断。

(9)

其中：η是两种群的相似度，∑Pij是两种群最优路径的相同路径段数目，即两种群的最优路径都包含路径段ij，则Pij为1，否则为0，Pse是两条路径所占据的路径段数目总和。

当两种群相似度较低时，需要加快算法收敛，进行种间竞争策略。即比较两种群各自的最优路径，将其中的更优路径替换另一种群的最优路径，如式(10)所示。

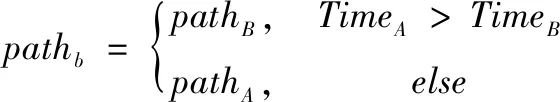
(10)

其中：pathb是两种群最优路径中的更优路径，pathA是种群A的最优路径，pathB是种群B的最优路径，TimeA是种群A最优路径的综合评定值，TimeB是种群B最优路径的综合评定值。

当两种群相似度较高时，需要防止种群陷入局部最优，进行种间合作策略，对两种群的信息素矩阵进行均化。将两种群的信息素矩阵相加并取平均值获得新的信息素矩阵，使用新的信息素矩阵替换原信息素矩阵，然后再进行迭代，如式(11)所示。

(11)

其中：Pheromonenew是进行平均后的新信息素矩阵，Pheromonei是两种群的原信息素矩阵。

2.5 信息素更新

传统信息素更新方法如式(12)和式(13)所示，每轮迭代后会更新蚂蚁找到的所有路径上的信息素，导致信息素积累过快，算法容易陷入局部最优。因此双种群蚁群算法在每轮迭代结束后只对各自的最优、最差路径进行奖惩，但算法收敛后最优、最差路径完全重叠，奖惩信息素浓度完全一致，路径上的信息素只挥发而不累积，导致蚂蚁迷失方向。

针对上述问题，综合考虑两种群之间的信息素交流，对两种群最优路径的重叠部分Pboth进行额外奖励，在惩罚最差路径时，定义路径Pwb为最差路径Pw和最优路径Pb的重叠路径，提出只惩罚Pw与Pwb的差集Pw_p，如式(14)～(17)所示。为了防止算法陷入局部最优，设置路径上的信息素浓度上下限，使信息素浓度始终在范围内。

(12)

(13)

(14)

Pw_p=PW-(PW∩Pb)

(15)

(16)

(17)

(18)

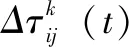
2.6 解决死锁问题

当环境复杂时，蚂蚁可能遭遇U型陷阱，由于在蚁群算法中蚂蚁不会重复选择已选择的节点，此时蚂蚁会陷入无路可走的状态，即发生了死锁，如图9(a)所示。针对这一问题，采取“填充陷阱”的策略，排除蚂蚁再次陷入同一陷阱的可能性。首先对死锁蚂蚁周围的节点进行判断，若该蚂蚁周围的八个节点仅有一个属于当前蚂蚁行走过的路径，则判定蚂蚁此时所在的节点是U型陷阱的底部，将该节点视为“障碍物”，即在地图矩阵中将该节点置1。随着迭代的进行，每次死锁都会在U型陷阱底部填充一个“障碍物”，U型陷阱会逐渐消失，不再引起死锁问题，填充后的路线图如图9(b)所示。

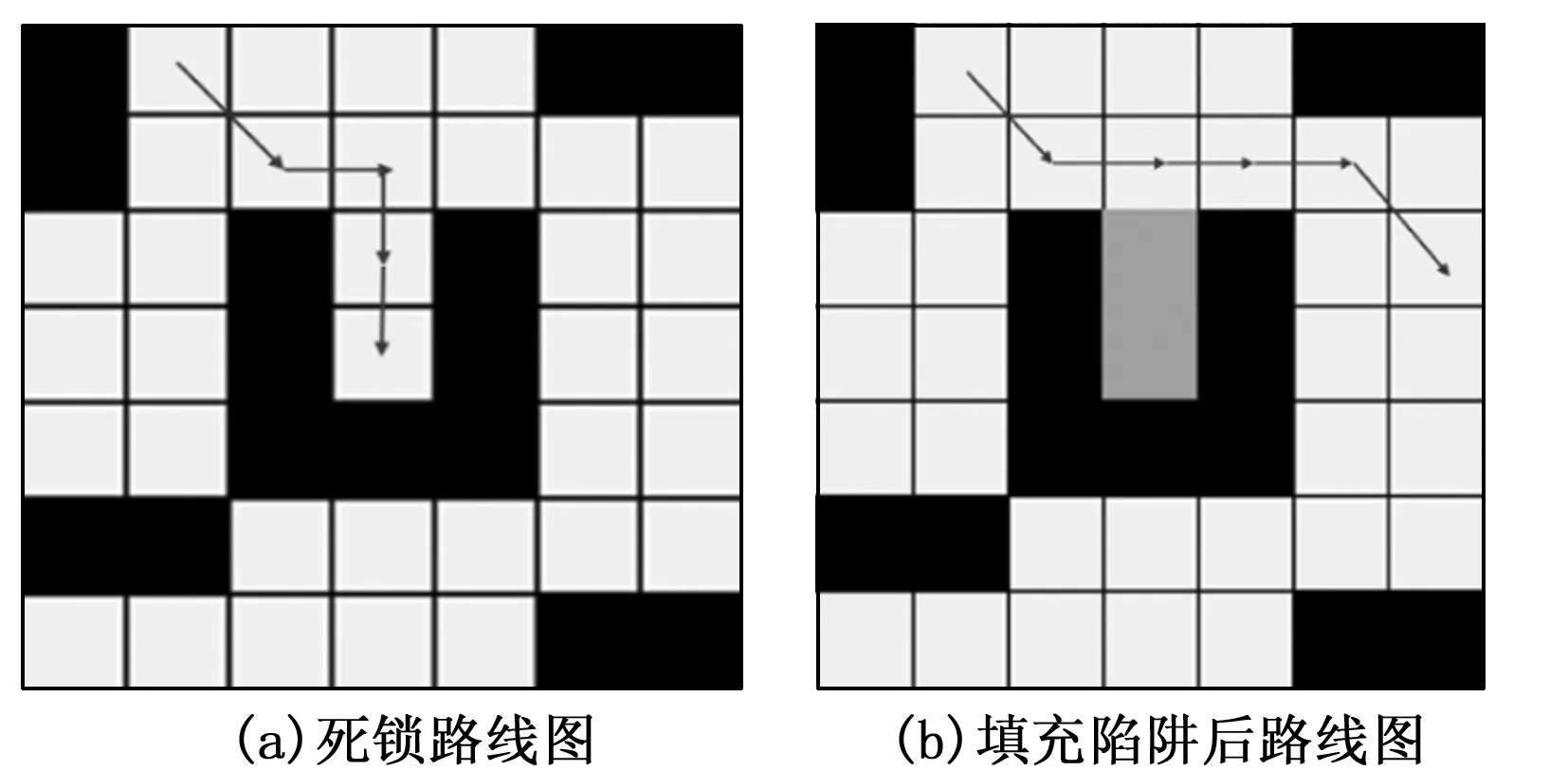
图9 死锁解决

3 算法流程

实现双种群蚁群算法的流程如图10所示，实现步骤如下。

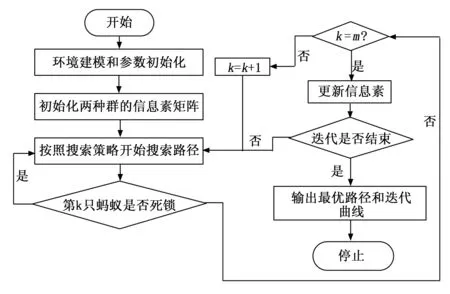
图10 双种群算法路径规划流程图

Step 1：对地图进行栅格法建模。

Step 2：初始化参数，如蚂蚁数量m、迭代次数、信息素启发因子α、期望启发因子β等。

Step 3：对两种群的信息素矩阵按式(3)进行初始化。

Step 4：计算本轮迭代的信息素启发因子α和期望启发因子β，判断本轮两种群蚂蚁数量是否达到最大值，若是则跳转至Step 8，否则，两种群蚂蚁数量各加1。

Step 5：种群A蚂蚁搜索周围8个栅格，并将符合条件的栅格加入候选列表；种群B蚂蚁按照图6搜索栅格，将符合条件的栅格加入候选列表。

Step 6：按照式(4)计算蚂蚁转移概率，利用轮盘赌确认转移栅格。

Step 7：判断蚂蚁是否抵达终点或死锁，若抵达终点，则返回Step 4，若死锁，则按照2.6节所述方法“填充”栅格，然后返回Step 4，否则返回Step 5。

Step 8：本轮所有蚂蚁完成一次搜索后，对所有有效路径进行排序，按照式(9)～(11)进行信息素交流后，按照式(14)～(18)更新两种群的信息素矩阵，更新完成后将两种群初始化。

Step 9：若达到最大迭代次数，迭代终止，输出最优路径并绘制收敛曲线，否则迭代次数加1，跳转Step 4继续搜索。

4 实验验证

4.1 仿真实验

为验证双种群蚁群算法的有效性，采用QT图形化工具作为开发环境，使用C++语言开发一种AGV路径规划仿真平台，PC配置如下：处理器为Intel(R)Core(TM)i7-10750H，主频为2.60 GHz，内存为16 GB。实验设置带有U型陷阱的20*20栅格地图和30*30栅格地图，对比双种群蚁群算法、单种群蚁群算法以及文献[19]提出的基于异构双种群全局视野的蚁群算法。其中单种群蚁群算法由2.1、2.2、2.5、2.6节组成，其信息素更新方式采用式(12)和式(13)。算法参数如表1所示。

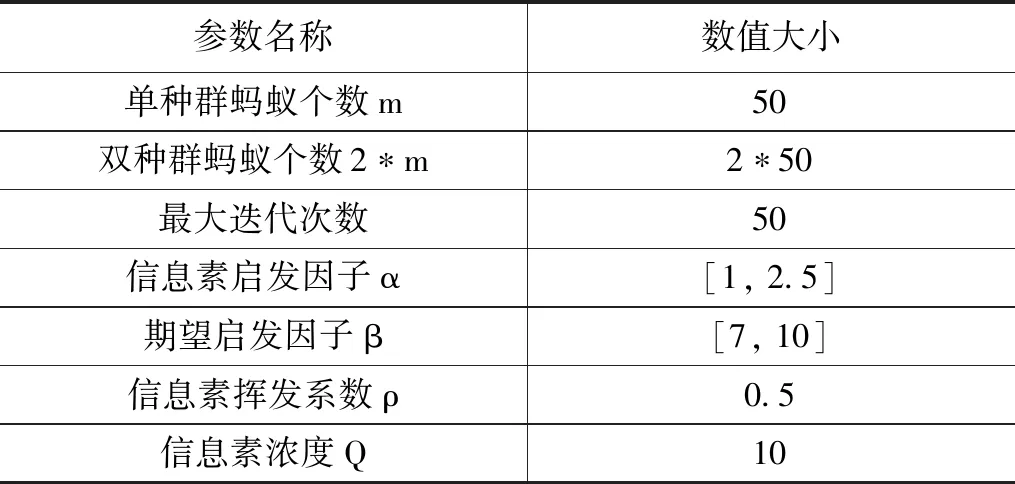
表1 算法参数表

图11～图13分别3种算法在20*20地图和30*30地图中的路径规划图和迭代曲线图，为避免偶然性对实验结果的影响，每种算法各进行20次仿真实验，对实验数据取平均值，对比4种算法的综合评价值、路径长度、90°转角数目和45°转角数目，如表2和表3所示。

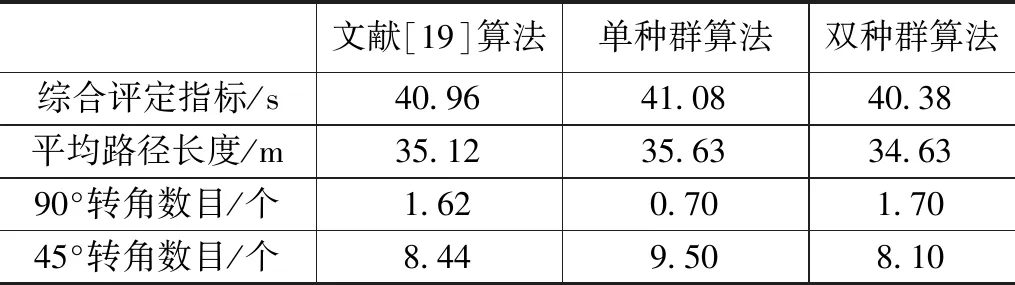
表2 20*20栅格地图仿真实验数据

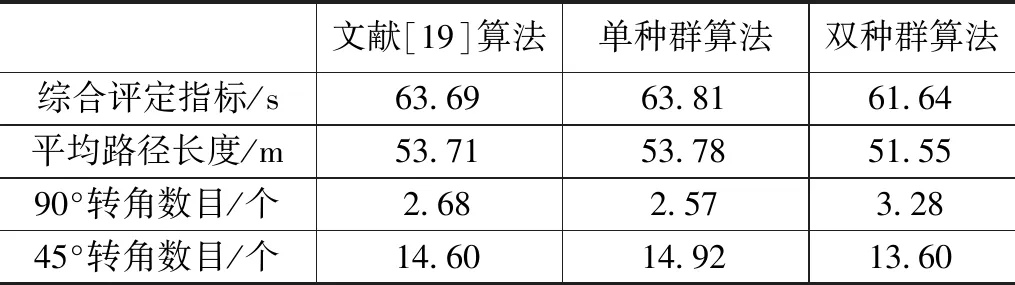
表3 30*30栅格地图仿真实验数据

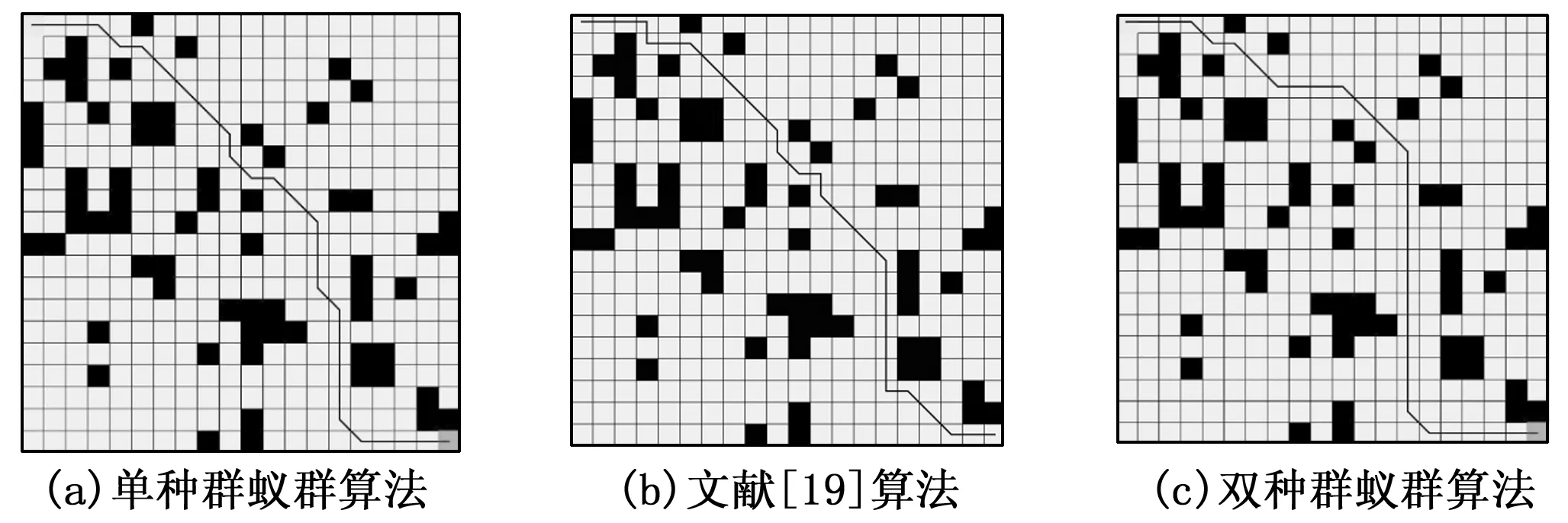
图11 20*20地图上3种算法的路径规划图

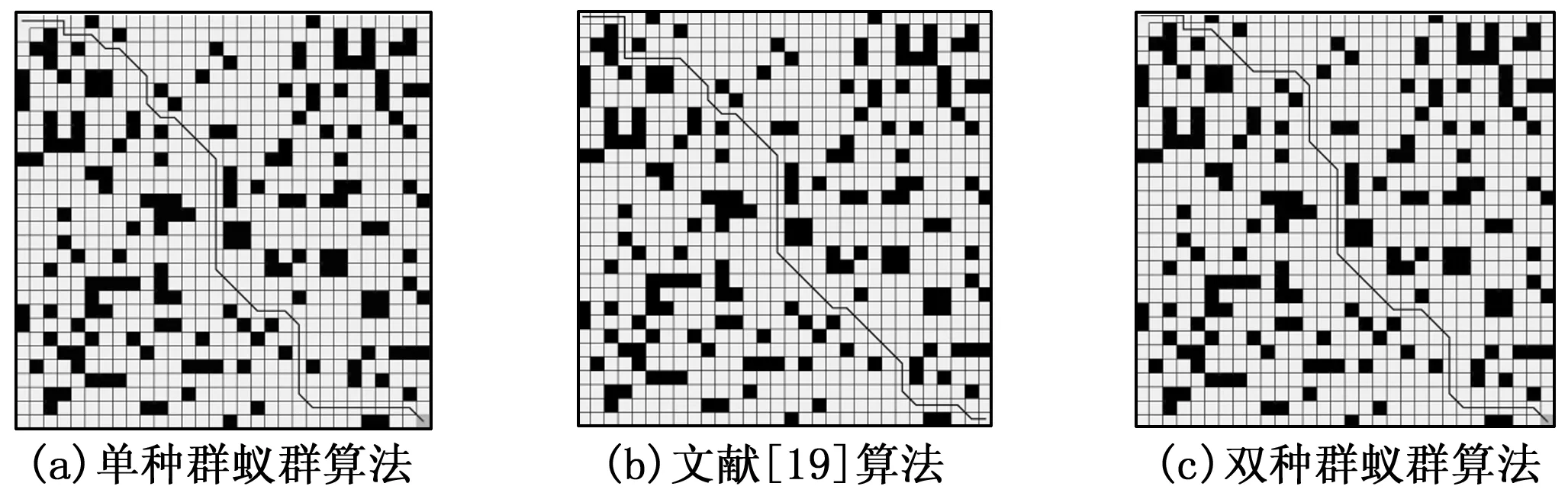
图12 30*30地图上3种算法的路径规划图

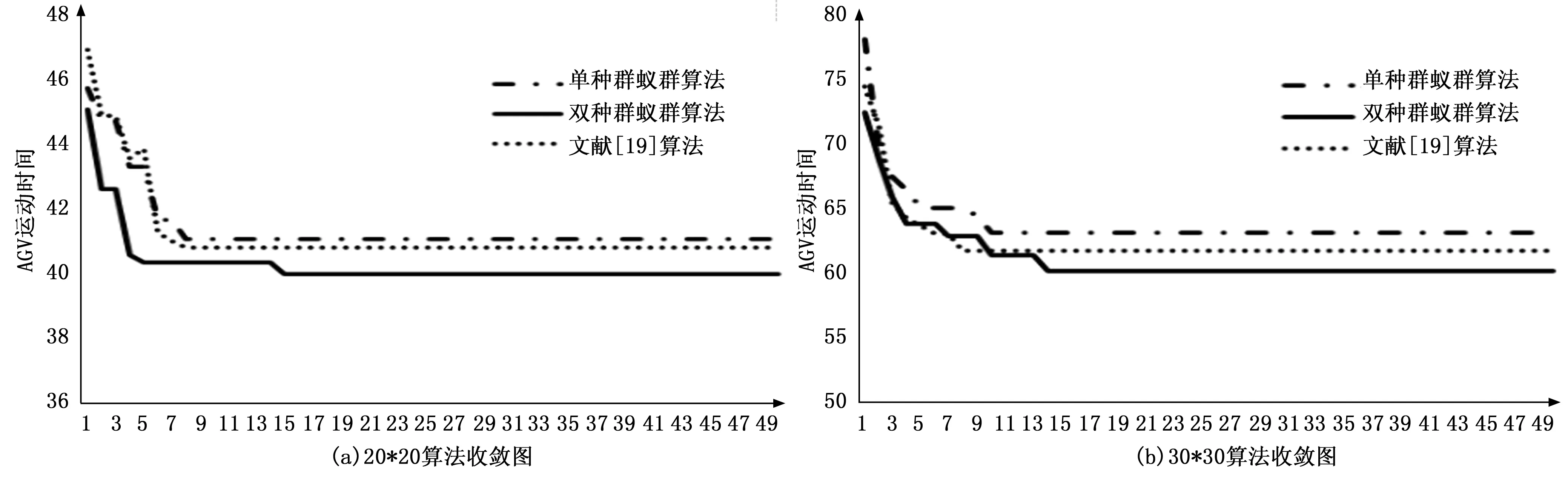
图13 算法收敛图

4.1.1 单种群蚁群算法与双种群蚁群算法对比

对比图11(a)、(c)和图12(a)、(c)，可以看出双种群蚁群算法规划的路线图比单种群蚁群算法规划出的路径更平滑，冗余拐点少。根据图13(a)及图13(b)可以看出双种群蚁群算法收敛速度更快，路径质量更高。对比表2和表3的数据，在20*20栅格地图中，双种群蚁群算法搜索的路径长度比单种群蚁群算法减少了2.8%。在综合指标方面，双种群蚁群算法比单种群蚁群算法减少了1.7%。相比于单种群蚁群算法，双种群蚁群算法减少了3.9%的拐角总数。而在30*30栅格地图中，地图复杂度更高，双种群蚁群算法搜索的路径长度比单种群蚁群算法减少了4.1%。在综合指标方面，双种群蚁群算法比单种群蚁群算法减少了3.4%。这是由于双种群蚁群算法具有自适应步长，可有效减少AGV在两点间的非必要拐弯，双种群蚁群算法依靠种群A与种群B在迭代早期的竞争搜索和迭代后期的合作搜索获得质量更高的解，双种群策略加快了算法早期的收敛速度，扩大了搜索范围，减少了路径的冗余拐点。

4.1.2 双种群蚁群算法与文献[19]算法对比

从图13可以看出文献[19]算法收敛速度更快，但双种群蚁群算法具有更强的突破局部最优的能力，其收敛曲线多次呈阶梯型下降，展现了良好的突破局部最优的能力。文献[19]将蚁群分为首领、中坚群体和追随者，通过两个种群分别进行深度搜索和广度搜索来寻找路径，并使用交叉算子融合种群最优解来进行种群间信息交流。而双种群蚁群算法在搜索早期两种群解的差异较大时，主要进行种间竞争策略，以此加快收敛速度，当算法逐渐收敛时，启用种间合作策略，均化两种群信息素矩阵，获得更大的搜索多样性，使得迭代曲线呈阶梯下降，更好的逼近最优解。

对比两者在不同尺寸栅格地图中的实验数据，在20*20栅格地图中，双种群蚁群算法搜索的路径长度比文献[19]算法减少了1.4%。对比两者的综合指标，双种群蚁群算法比文献[19]算法减少了1.2%。较之于文献[19]算法，双种群蚁群算法减少了2.5%的拐角总数。随着地图的进一步复杂化，在30*30栅格地图中双种群蚁群算法规划的路径长度比文献[19]算法减少了4.0%。在综合指标方面，双种群蚁群算法比文献[19]算法减少了3.2%，此外，双种群蚁群算法的拐角总数比文献[19]减少了2.3%。结果表明双种群蚁群算法在路径长度、AGV运行时间、转弯次数3个方面均优于文献[19]算法，说明双种群蚁群算法通过差异化种群步长和自适应交流策略获得了更优秀的寻优能力，且随着环境的复杂化，算法性能之间的差距被进一步放大，双种群蚁群算法依靠种群间信息素的相互交流兼顾了收敛速度和路径质量，使其在复杂环境下依然有良好的收敛性及路径质量。

4.1.3 不同地图对比实验

为验证算法的通用性，分别使用文献[5]、文献[9]、文献[10]、文献[19]中栅格地图进行路径规划，其中文献[10]地图为凹槽地图，存在大量U型陷阱，文献[19]地图是回廊地图，回廊地形空间狭小，容易陷入局部最优，4种地图的规划结果如图14所示，双种群蚁群算法在回廊地图、凹槽地图中都可以规划出一条可行的较优路径，且基于图4所所示的防撞设定，双种群蚁群算法规划出的路径更为安全。

图14 不同地图上的路径规划图

4.1.4 真实环境中的AGV路径规划

为了保证理论的准确性，将双种群蚁群算法应用于实际的工程环境中。以图15所示为某公司半导体加热管道生产车间为实验对象，实现加热管道的自动运输，车间内环境复杂，工位之间较为紧凑，障碍物众多。采用搭载树莓派的ROS小车进行物料运输，小车尺寸为410*407*153，搭载RPLIDAR A1型激光雷达、MPU6050惯性传感器，通过PC端使用SSH远程登录的方式连接树莓派实现小车的远程控制，小车在树莓派中安装ubuntu18.04操作系统，并通过ROS系统实现建图、定位和导航，小车的运动控制由STM32单片机分别控制4个麦克纳姆轮实现，使用拓展平台承载货箱，载重30 kg，如图15(a)所示。小车匀速行驶速度为0.4 m/s，最大角速度为0.5 rad/s。

图15 AGV小车车间实验

利用SLAM算法在ROS系统下构建环境地图，使用双种群蚁群算法进行全局路径规划，并利用Rviz组件在所得环境地图上实时显示导航结果，如图15(b)所示，其中深色部分为加工工位和检测区。当遭遇行人等动态障碍物时，小车以双种群蚁群算法规划出的全局路径为引导使用动态窗口法(DWA，dynamic window approach)进行局部路径规划，绕过障碍物。如图15(c)所示，图中圆圈标出的位置为行人的路径轨迹，小车在原路径受阻后进行局部规划，绕开行人后回归到双种群蚁群算法规划的全局路径。实验结果表明该算法可以为小车规划一条安全可靠的行驶路径，实现物料的有效运输，验证了双种群蚁群算法的可行性和准确性。

5 结束语

随着智能化工厂等产业的飞速发展，仓储物流相关技术成为研究热点之一。双种群蚁群算法针对斜向运动可能存在的AGV碰撞问题，提出严格的判定条件，有效保证了路径的安全性；为了解决蚁群算法中常出现的死锁问题，提出了将符合条件的死锁单元格视为障碍物的“填充陷阱”策略；针对蚁群算法初期盲目搜索、容易陷入局部最优、原启发函数引导作用弱等问题，采用了差异化初始信息素、修改启发函数、使蚂蚁获得自适应步长、双种群合作搜索以及对部分路径进行信息素奖惩等策略。仿真实验表明，双种群蚁群算法可以有效减少路径长度和冗余节点，该算法具有良好的收敛速度和突破局部最优的能力。为验证该算法在实际工程环境下的可靠性，采用ROS小车在某车间环境下进行路径规划，验证了算法的可行性。