基于FOPID+ADRC的永磁同步电机低速控制

冯光权，董 涵，冯浩文

(1.贵州中航电梯有限责任公司，贵州 遵义 563000；2. 湖北汽车工业学院 电气与信息工程学院，湖北 十堰 442002)

0 引言

永磁同步电机是一种以永磁体为转子的同步电机，具有高效率、高功率密度、高精度控制和良好的动态响应等优点[1-2]。这种电机在许多领域得到了广泛应用，例如工业生产、交通运输、医疗设备和家用电器等[3-4]。近年来，永磁同步电机得到了越来越多的关注和研究。随着电力电子技术、微电子技术和计算机技术的不断进步，永磁同步电机的控制性能和应用范围不断扩大[5]。同时，由于稀土永磁材料的价格和供应问题，研究人员也在探索新的永磁材料[6]和磁场强度设计[7]方法，以提高永磁同步电机的性能和降低成本。然而，PMSM在运行过程中也存在非线性、不确定性和多变量等问题。因此，研究PMSM控制技术具有重要的背景和意义。

近年来，学术界广泛关注FOPID控制[8]。FOPID控制将传统整数阶PID控制器扩展到分数阶PID控制器，引入FO微分和分数阶积分两个额外参数[9]，从而扩展了系统的动态调节范围[10]。因此，相比传统PID，FOPID控制具有更好的控制性能[11-12]。刘红艳等提出了一种FO模糊ADRC的机械臂轨迹跟踪控制[13]，实现了FOPID参数的实时优化，提高了系统的整体控制性能。张瑶等提出了HPSO-FOPID算法[14]，解决了机器人焊接过程中焊缝跟踪性能的问题，孙浩等设计了一种模糊FOPID控制器[15]，利用模糊规则来调整FOPID参数，以提高FOPID控制器的响应速度和鲁棒性。

本文提出了一种改进的自抗扰控制器，用于永磁同步电机控制。该方法基于非线性自抗扰控制器的非线性函数，并解决了原点附近的高频抖振问题[16]。首先，建立了永磁同步电机的动力学方程和数学模型。接着，采用一种新型的非线性函数替代原有的非线性函数。然后，使用模糊控制器对FOPID的参数进行设置[17]。最后，将NLSEF用FOPID代替以提高系统的动态性能[18]。仿真结果表明，改进后的自抗扰控制器比传统自抗扰控制器在跟踪精度和抗干扰能力方面表现更好。

1 永磁同步电机转速环扰动分析

永磁同步电机的运动方程表示为：

(1)

式中，TL为负载转矩；p为极对数；ωr为电机输出的角速度；B、J分别为电机的摩擦系数和转动惯量；b(t)为未知扰动。

根据电机的电磁转矩方程可得到电机角速度表示为：

(2)

其中：

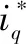
2 改进ADRC控制器设计

改进ADRC控制器框图如图1所示，控制器由三部分组成：1)非线性微分跟踪器(TD，tracking diferentiator)用于跟踪信号，包括差分信号；2)扩张观测器用于观测系统内部的状态，估计系统的不可预测状态；3)FOPID用于将TD和ESO的输出进行非线性组合，结合扰动提供稳定的输出信号。

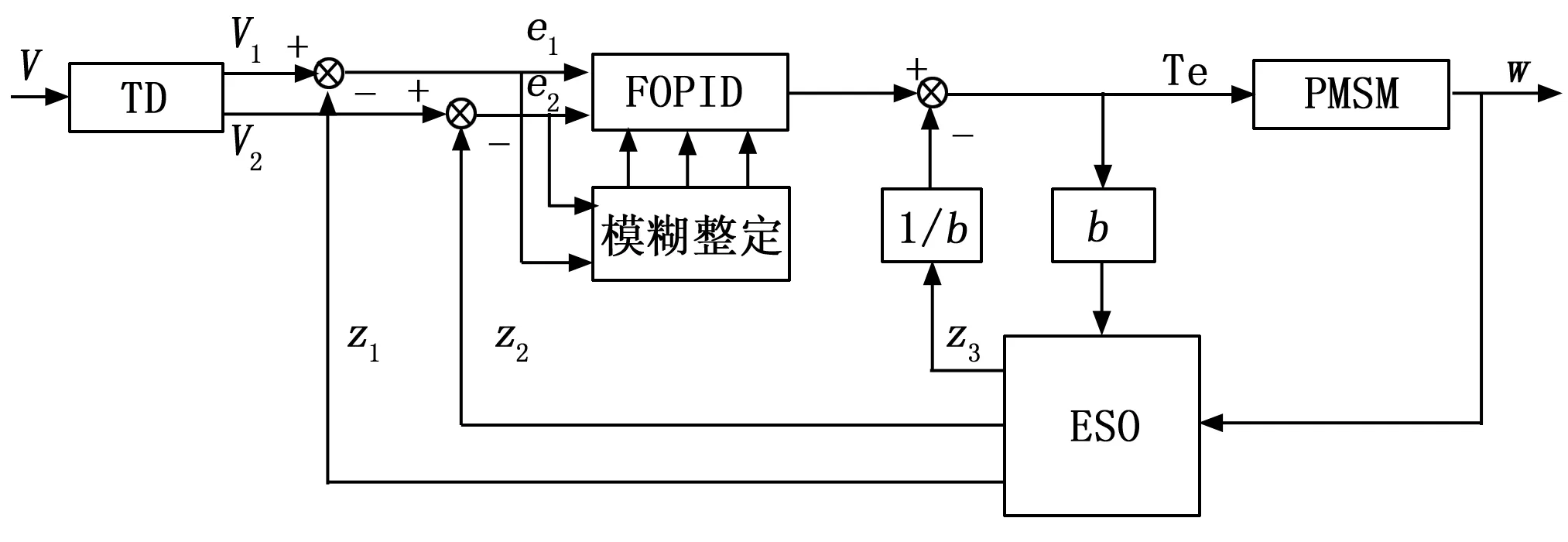
图1 改进ADRC控制框图

2.1 微分跟踪器设计

微分跟踪器的作用是通过自抗扰控制中的非线性函数将参考信号和输出信号的差值处理后得到平滑的输入信号[19]，TD算法表示为：

(3)

式中，v(t)为输入信号；h为积分步长；r为跟踪因子；fhan为非线性函数。

其表达式如下：

(4)

TD利用输入信号的跟踪和滤波特性，通过安排适当的过渡过程可以有效的缓解设定值突变引起的输出突变和超调，从而减少响应速度和超调量。

2.2 改进扩张观测器设计

ESO是ADRC的核心部分，其基本原理是将被控对象的输出扰动扩展为新的状态变量，并通过特殊的机制建立反馈[20]。利用ESO可以通过反馈中的补偿来估计未知的外部扰动和内部的变化。ESO仅受输入和输出信号的影响，并不依赖于被控对象的数学模型。ESO算法表示为：

(5)

式中，ω为输入信号；e为观测误差；Z1为输入信号的跟踪信号；Z2为输入信号的微分信号；Z3为系统扰动的观测信号；a1，a2，a3为跟踪因子；δ为滤波因子；β1，β2，β3为ESO输出误差校正增益；b0为补偿因子；u为系统输出；fal(e，a，δ)为最优控制函数，其表达式为：

(6)

式中，sgn为符号函数。

由上式可知，δ和-δ是该函数的两个分段点，对该函数求导可得：

(7)

(8)

在不同分段点上，导数是不同的，因此，原函数在段点处不可导。虽然fal函数在原点和段点是连续的，但它是不可导的，缺乏连续性和平滑性。因此，对fal进行改进，得到新的函数fnal，使其在原点和段点处具有良好的连续性和平滑性。

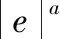
当|e|<δ时，fnal=psin(e)+qe2+rtan(e)。

这里选择多项式和三角函数相结合的插值法时因为在fnal函数中δ的值通常小于1，在此区间内，sin(e)的平滑性由于e，tan(e)的收敛性由于e3。

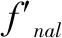
(9)

为了对比fal和fnal的区别，这里取δ-0.01，a=0.25，对比图如图2所示。

改进ESO的表达式为：

(10)

2.3 模糊分数阶PID控制器设计

FOPID是传统整数阶PID的扩展，其传递函数表达式为：

(11)

式中，KP为比例常数；KI为积分常数；KD为微分常数；λ和μ分别为积分项阶数和微分项阶数。

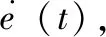
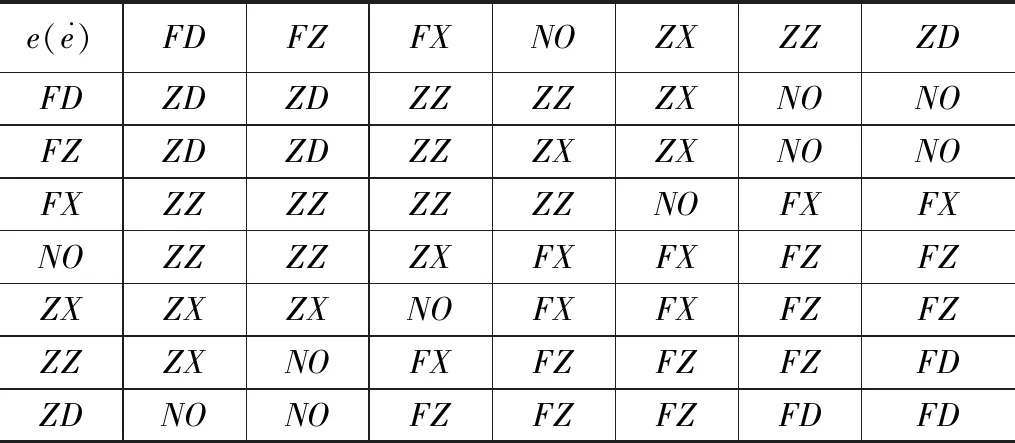
表1 KP模糊规则表

表2 KI模糊规则表

表3 KD模糊规则表

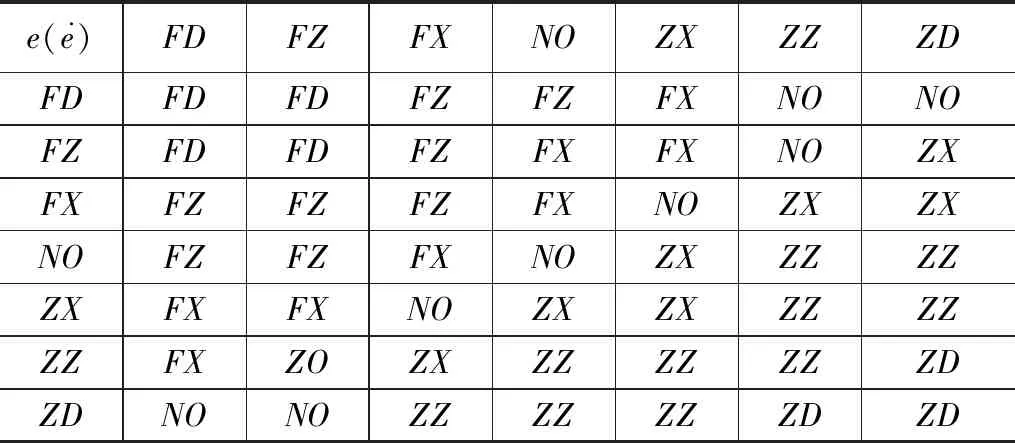
表4 λ模糊规则表

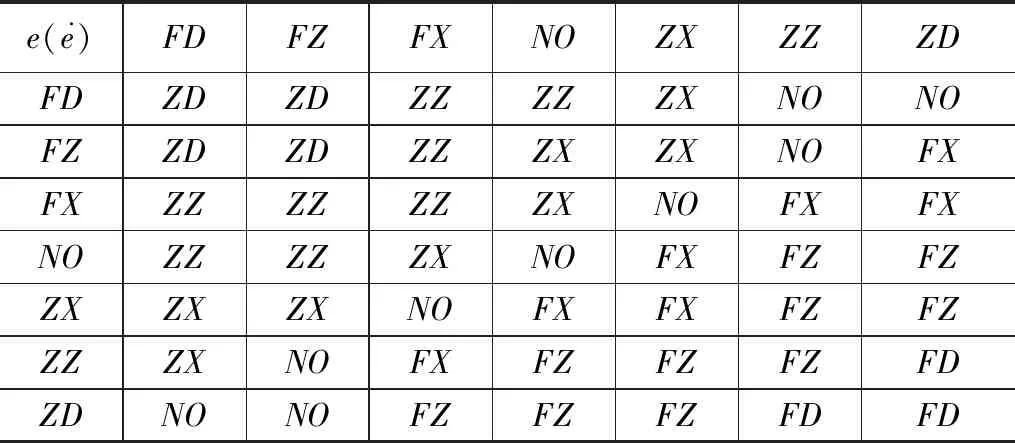
表5 μ模糊规则表

图3为KP的隶属度函数图，其余4个参数的隶属度函数图除论域不同外，其他的都相同。

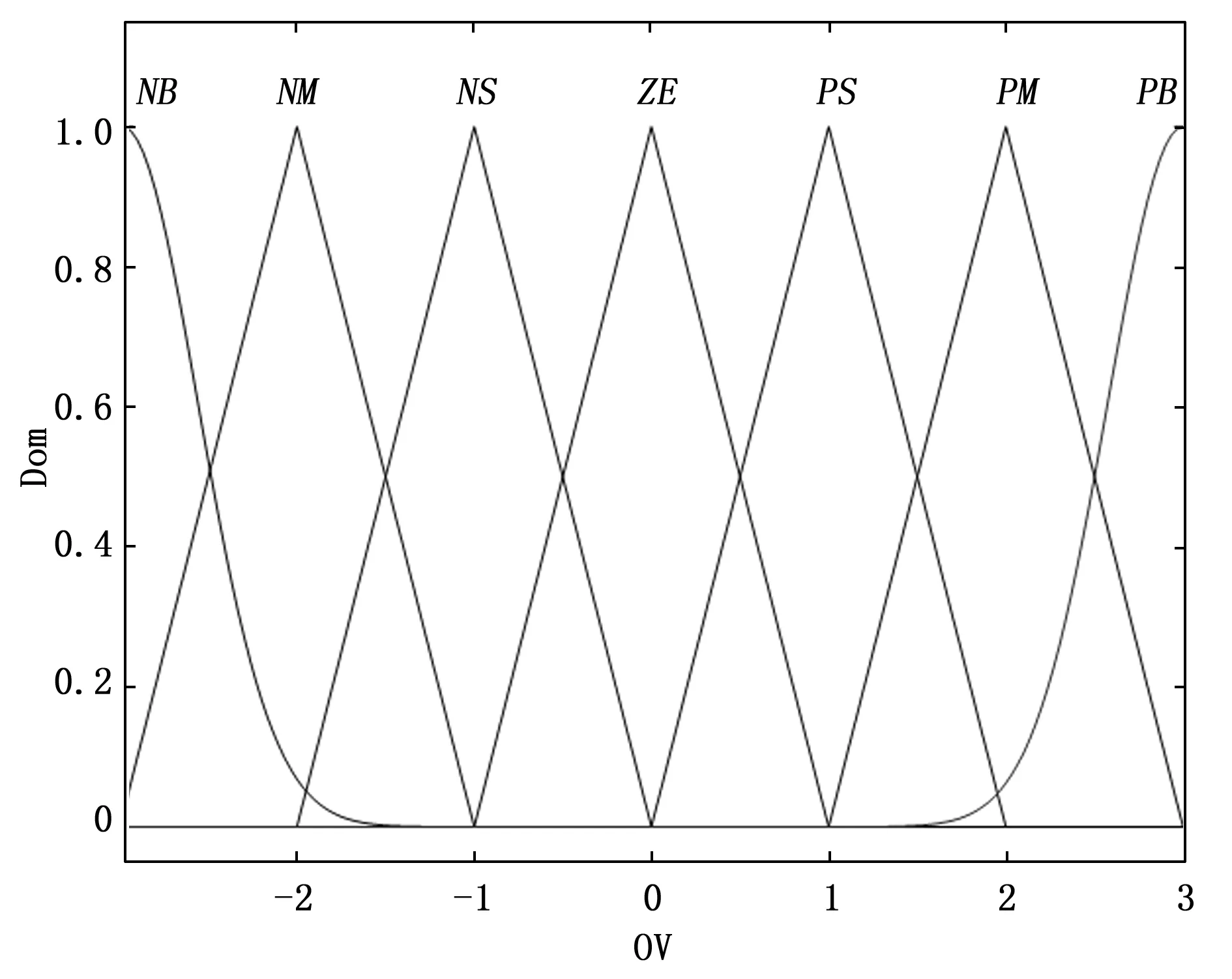
图3 KP的隶属度函数图

KP，KI，KD，λ，μ根据模糊规则表调整如下：

(12)

2.4 系统稳定性分析

将上述电机模型写成：

(13)

二阶ESO的数学模型为：

(14)

设s1=s，s2=m(t)，w(t)=-m(t)，式(13)可表示为如下表达式：

(15)

设e1=z1-s1，e2=z2-s2，e=e1，则状态误差方程为：

(16)

将下列动态反馈补偿应用于系统：

U1=U10-z2

(17)

由于ESO采用非线性结构，难以用传统观测器设计理论分析。因此，结合自稳定性理论[21]分析本算法的稳定性。

定义以下函数来分析ADRC+FOPID的稳定性：

(18)

(19)

q2i(e1i，e2i)=e2i-e1i+kp1i(e1i)sign(e1i)

(20)

(21)

根据文献[21]中的自稳定性判断条件，只需要证明下列条件成立：

(22)

(23)

也就是v1<0时，系统时稳定的。

证明：设

(24)

将式(22)和(23)两式带入式(24)当中，可得下式：

(25)

通过上式建立以下表达式：

(26)

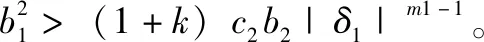
当q2i(e1i，e2i)≤p1ie1i时：

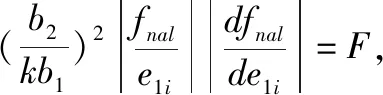
Fe1i(e2i-b1e1i)≤Fe1i(-kp1isign(e1i)+p1i)=

F(-kp1i|e1i|+p1ie1i)<-F(k-1)p1i|e1i<0|

至此，系统稳定性证明完毕，系统是稳定的。

3 仿真分析

本文主要研究的是用FOPID+ADRC控制器代替传统ADRC控制器，将该控制器与PMSM相结合，与ADRC控制器做出对比，验证其控制精度。在相同的输入条件下分别对传统ADRC和ADRC+FOPID进行仿真，验证所提出的ADRC+FOPID在永磁同步电机中的性能。系统仿真模型如图4所示。

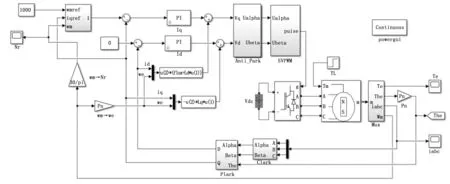
图4 系统仿真模型图

仿真采用的PMSM参数如表6所示。

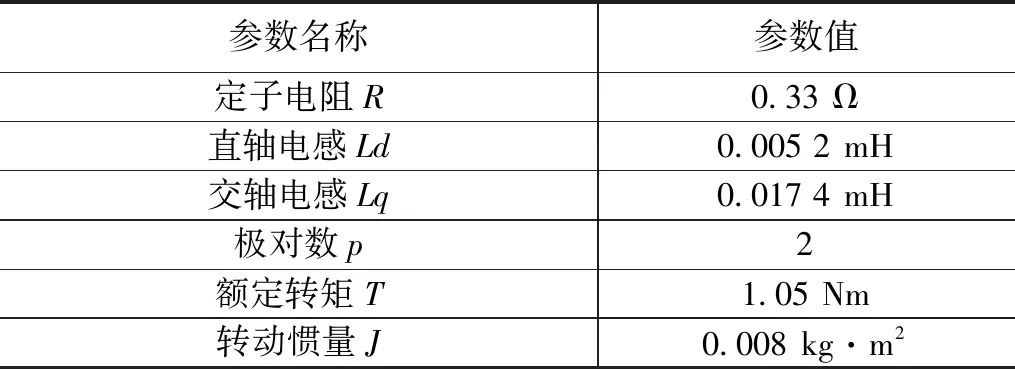
表6 永磁同步电机参数表

ADRC+FOPID参数设置如表7和表8所示。

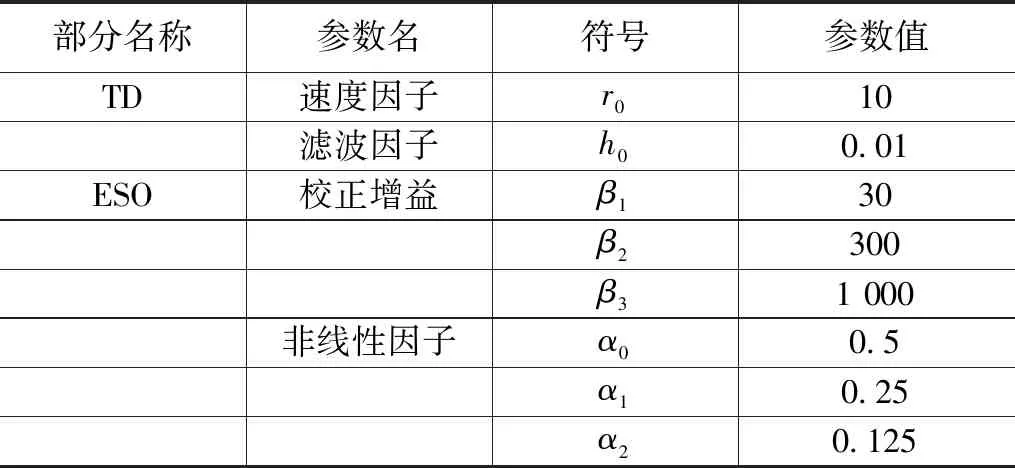
表7 ADRC参数设置表

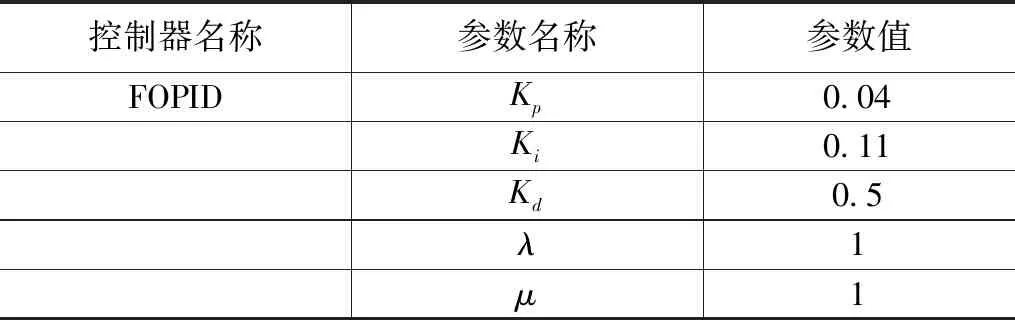
表8 FOPID参数设置表

将所有参数设置完成后，设置仿真时间为0.4 s，进行下列的仿真实验。

在电机空载时分别设置额定转速为100 r/min，200 r/min和1 000 r/min进行ADRC+FOPID与ADRC控制效果对比试验，其转速控制对比图如图5(a)，(b)，(c)所示。

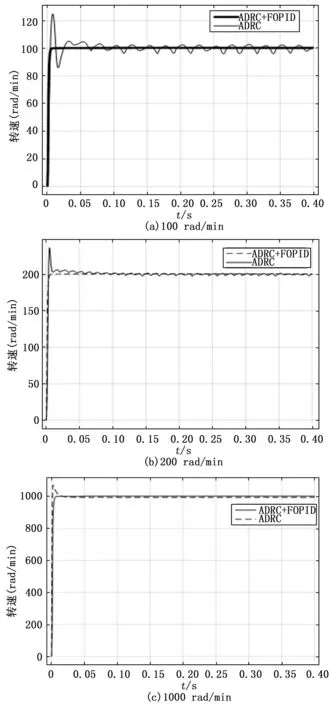
图5 空载转速试验对比图

由图5(a)，(b)可以看出，电机在100 rad/min和200 rad/min低速运行时，ADRC+FOPID的超调量、响应速度以及达到稳态的时间均要优于传统ADRC，由图5(c)可以看出在1 000 rad/min时两者的控制效果区别很小，因此可以得出一个结论：ADRC+FOPID在电机低速空载运行时的控制效果要明显优于传统ADRC。

在电机空载时进行转速突变的试验，分别设置初始转速为200 rad/min和1 000 rad/min，并在0.2 S后突变为300 rad/min和1 500 rad/min。其转速控制对比图如图6(a)，(b)所示。

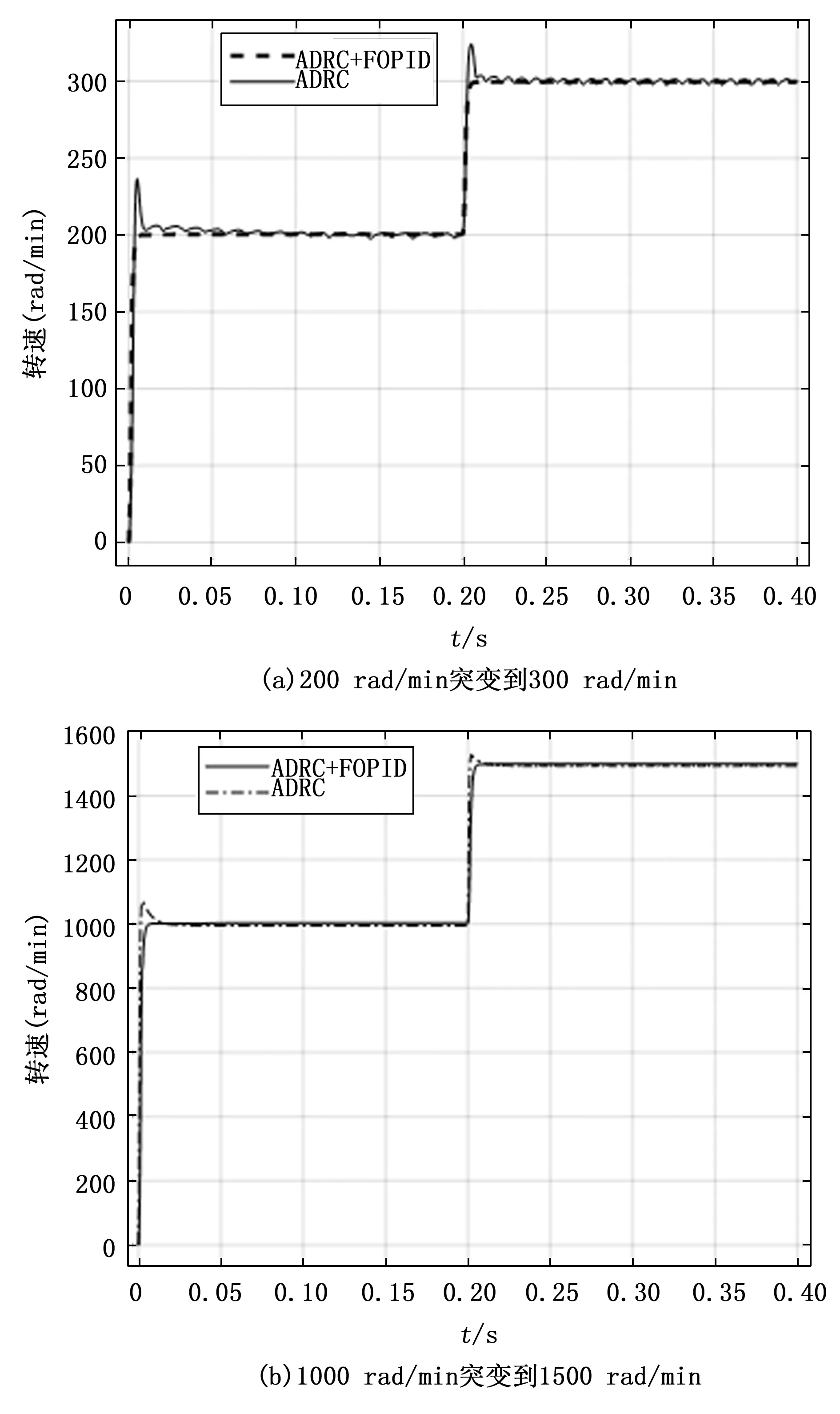
图6 空载转速突变试验对比图

由图6(a)可以看出在传统ADRC控制下，电机不能在低速情况下稳定运行，而ADRC+FOPID则可以使电机稳定运行，且具有良好的转速跟踪特性。由图6(b)可以看出电机在高速运行时，ADRC+FOPID只是略优于传统ADRC，都能使得电机稳定运行，且都具有良好的转速跟踪特性。因此可以得出一个结论：当电机低速运行时：ADRC+FOPID相比于传统ADRC具有良好的控制效果和稳定的跟踪性能，但在高速运行时两者的控制效果相差甚微。

在电机空载时进行加载试验，给定初始转速分别为200 rad/min和1 000 rad/min，并在0.2 S时加上10 N·m的负载，得到图7(a)，(b)所示的转速控制对比图。

由图7(a)可以看出，电机在200 rad/min低速运行时，当受到干扰后，传统ADRC并不能使得系统恢复稳定，而ADRC+FOPID能够使得系统快速恢复稳定运行。由图7(b)可以看出，电机在1 000 rad/min高速运行时，两种控制方法均能在系统受到干扰后恢复稳定，但ADRC+FOPID的恢复速度要由于传统ADRC。因此可以得出一个结论：ADRC+FOPID的鲁棒性和抗干扰能力要优于传统ADRC。

4 结束语

本文以PMSM为研究对象，设计了一款ADRC+FOPID控制器，该控制器由三部分组成：TD，ESO，FOPID。ESO中新的函数改善了原点的连续性和平滑性，TD改善了信号的过渡过程，FOPID改善了系统的控制效果。将该控制器与传统的ADRC控制器进行对比试验，验证其控制效果。结果表明，在电机低速运行时，ADRC+FOPID的跟踪效果，响应速度，鲁棒性及抗干扰能力均要优于传统ADRC，但在电机高速运行时，控制效果只是略优于传统ADRC。后续将针对电机在高速运行的控制效果对控制器进行相应的改善和调节。