4秒微重力实验舱导轨副轴承故障分析

张运山，席 隆

(1.中国科学院大学，北京 100094；2.空间应用工程及其技术中心，北京 100094)

0 引言

随着航天事业的发展，人们已经开始步入太空时代，越来越多的国家已经进入了太空资源的争夺中，然而太空是与地面完全不同的环境——微重力环境。为了能更加清楚清晰的认识在太空环境中的一系列问题以及独特的物理现象，人们开始逐步建立起落塔，从而可以在微重力环境中进行有效的地基实验。

在地面获得微重力的手段主要有落塔或落井，如今世界上不少国家根据空间基础交叉科学研究的需要，完成了地基微重力实验设施的建立。比如美国NASA的格林2.2 s落塔和Zero-G 5.18 s落井，分别可以实现10-3g和10-5g的微重力水平，澳大利亚的微重力落塔自由落体时间为2秒自由落体距离为20米，中国NMLC的北京落塔实现60米的自由落体距离，塔高100米，可实现自由落体时间为3.6 s，实现10-3-10-5g的微重力水平，日本JAMIC的10 s落井有490米，可实现10-5g的微重力条件；MGLAB的4.5 s落塔入地150米也可实现10-5g的微重力条件，同时德国的不莱梅落塔是双程落塔塔高146米，自由落体距离为110米可实现10-6-10-7g的微重力条件。

4秒微重力落塔就是在地面模拟太空微重力环境进行实验舱加速上升到匀速上升最终进入自由释放的过程。根据微重力装置的俯视图如图1所示，其中直线电机动子导轨的精确度要求并不是特别高，本身在运行的过程中就会有较大的力压在上面，主要是完成给实验舱提供足够推力，所以在一定的震动下都是允许的范围之类的，故研究对象是精度要求更高的实验舱导轨副装置。实验舱导轨装置是保证实验舱在整个上升和自由落体过程中相对稳定，减少晃动。

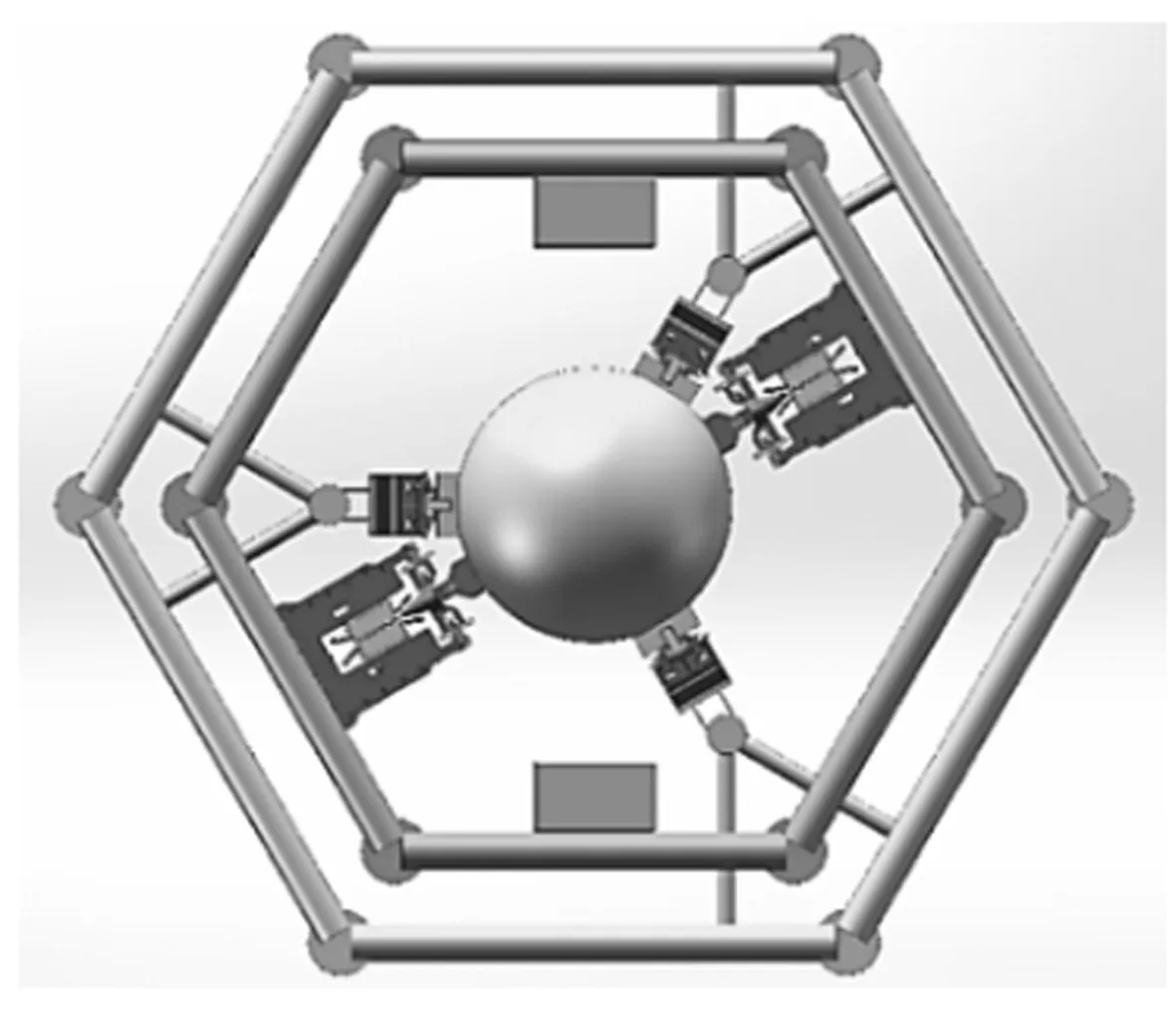
图1 微重力装置俯视图

实验舱导轨副采用的是“滚轮+直线高速导轨”的设计，实验舱上下共布置5组滚轮机构。内塔上安装3根T形高速导轨，周向均布，每条导轨较长。滚轮在导轨左右两侧夹紧，可以在导轨上高速平顺移动，如图2所示。

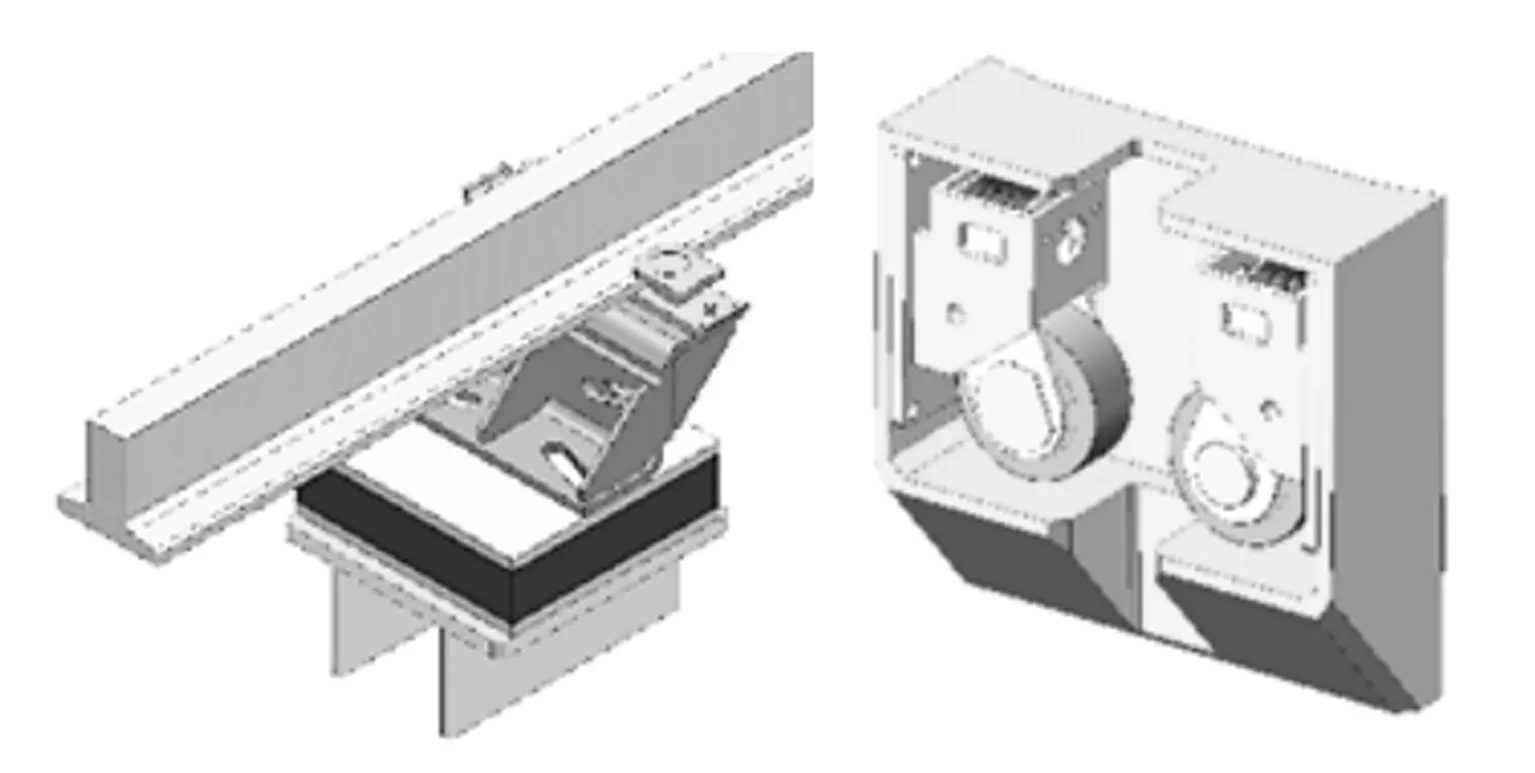
图2 实验舱导轨副设计

随着科技的进步对于各项系统的稳定性及安全性越来越得到大家的重视，一个系统能否安全稳定不仅关系到一个项目的成功与否，更可能对整个项目造成巨大的经济损失甚至更严重的情况会对成员的生命安全造成巨大的威胁，即使项目中再容易被忽略的小故障都可能时间的推移以及实验次数的增加，不断传播造成难以估计的严重后果。如2021年6月13日，湖北省十堰市的一个集贸市场发生了一起重大的燃气爆炸事故，导致26人死亡，138人受伤，其直接原因是未发现并及时排除出该重大隐患；2018年12月26日，北京交通大学发生了一次实验室爆炸事故，导致了三名实验的学生死亡。这些因为种种不起眼的小问题导致的大事故一直都时有发生，所以对于整个安全问题上都要谨小慎微，从而故障分析以及健康诊断也逐步成为大家越来越关心注意的问题。

应对在4 s微重力落塔的背景下，考虑到实验舱是整器中最重要的一部分，如果实验舱出现问题，那么对于整个4 s实验装置来说影响是非常巨大的。在整器中最容易出现故障的地方就是实验舱导轨副系统，而在实验舱导轨副系统中轴承部件又是最频繁出现故障的部位，所以先针对实验舱导轨副最易出现故障的滚动轴承部件进行一个深入研究，再考虑整体导轨副各部件之间的故障模式的关联影响。

实验舱导轨副轴承在长期运行下，极易出现磨损等问题，导致各项指标出现偏差，一旦指标出现了变差，轻者会出现数据不够严谨，严重的情况甚至会导致整个实验装置的报废[1]。经过多方面调研，可以确定滚动轴承故障中的90%都是有内外圈的故障导致的[2]，其中点蚀故障更是其中的重要因素之一，所以将导轨副组件中的轴承部件先具体提出进行单独建模分析，是极有必要的。在轴承故障分析中，对于故障的特征频率的提取是完成故障诊断的重要环节[3-5]。

考虑到目前国内外的研究现状，对于轴承的建模方法已经比较成熟[6]，如通过脉冲序列通过故障区域时产生的冲击振动[7-10]，或者是考虑到通过故障处的形变，导致接触载荷时会发生一定的突变，导致轴承产生冲击[11-14]。对于滚动轴承故障的常用的分析方法一般为时域法，在时域上对于轴承进行一定的监测分析，观察相应曲线。但为了较清楚的分析出轴承故障所受到的规律，通常也会采用频域分析，通过频谱图分析结果，故有了包络解调分析[15]。在文献[16]和[17]中McFadden等人就提出了包络解调分析法，并在频域上通过该方法在轴承的内环实现了单点点蚀和多点点蚀两种故障模型的建立。在文献[18]中TANDON等人继续将包络解调分析法进行更加广泛的应用，并针对在各个滚动轴承元件上的单点点蚀故障问题进行分析，验证方法的可行性。文献[19]中杨将新等人结合之前轴承内外环的单点点蚀故障模型，加入系统噪声去验证该方法，再有扰动干扰的情况下去验证了包络解调分析法。且结果完全符合滚动轴承在受到非平稳信号时所应有的结果特征[20-21]。

考虑到前人大多采用的是先通过数学建模之后再经过龙哥库塔迭代仿真的方法，本文将采用不一样的仿真方法去验证实验结果以及进行分析。同时大部分在轴承故障诊断的对比实验都是凯斯西储大学的实验数据，采用的都是SKF6205型轴承，验证性较强但是实用性不够，在工程中不会都使用该类型轴承。本文将根据具体实验舱导轨副使用的轴承部件，结合轴承在实际运动过程中的条件，考虑到实际工程中的情况进行故障判断分析。同时在完成了轴承部件分析之后去考虑到对于整个导轨副部件的故障影响，目前较多的导轨副是运用在铁路和机床上是水平导轨副，本文是运用在微重力实验舱中的竖直导轨副，也有一定的创新性探索，具有一定的实际意义和理论基础。

1 系统模型及原理

根据实验舱导轨副简化后如图3所示，其中包括滚轮固定板、滚轮摇臂、插销、导轨以及轴承。

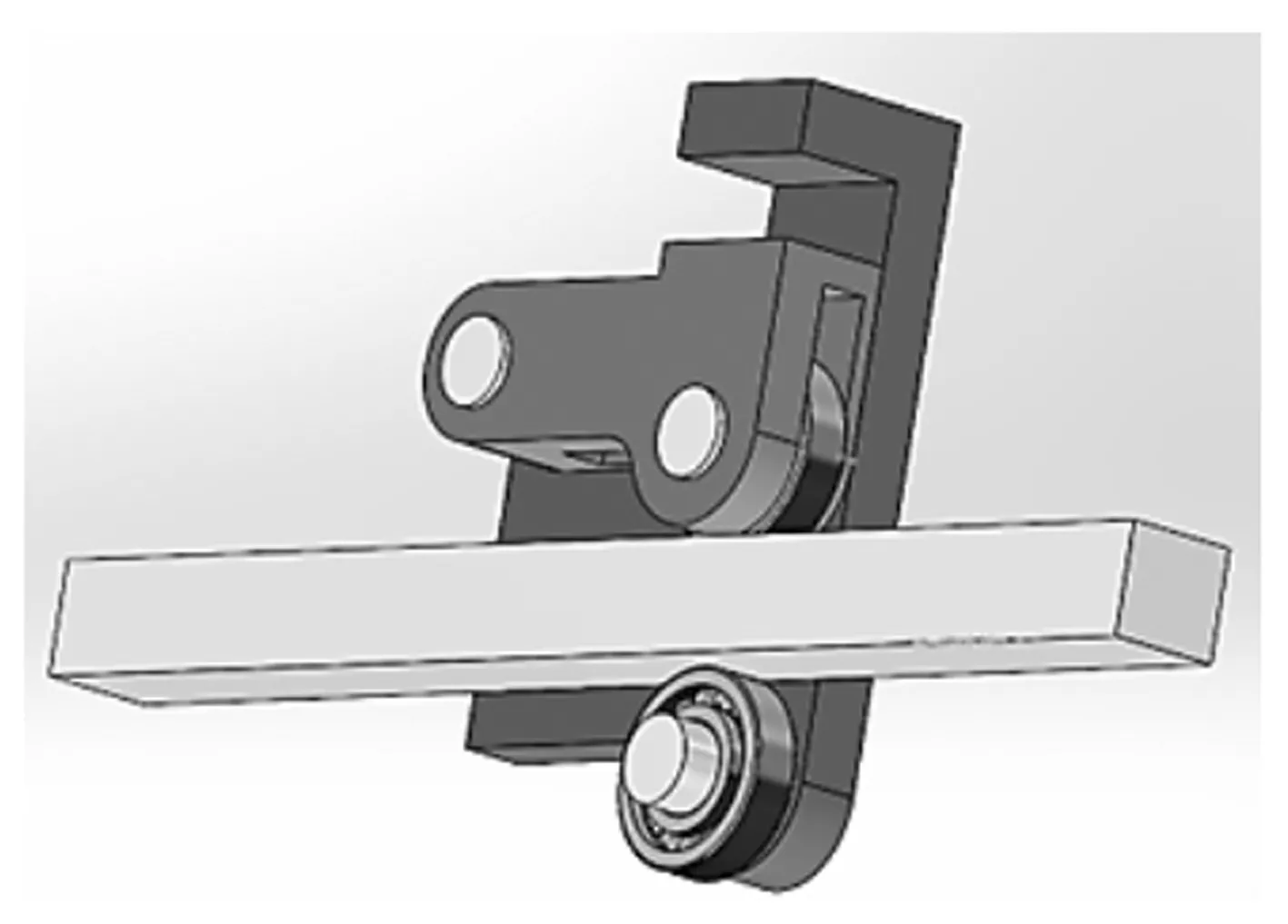
图3 实验舱导轨副简化图

通过滚轮固定板将各部件固定住，导轨在两个滚动轴承中，同时在滚轮摇臂上可以施加压力将滚动轴承和导轨夹紧，完成上下滑动。

提取出轴承进行单独建模，如图4是滚动轴承的典型结构示意图，可以了解到轴承的具体组成为轴承的内环和外环，滚动体(滚珠)以及保持架。保持架起到很好的支撑和保护滚子的作用，使得滚子在内环和外环的凹槽内进行滚动。具体一些参数规范表示为：内圈滚道平均半径为Di；外圈滚道平均半径Do；滚动体中心所在圆的直径为D；滚动体的平均直径d；滚珠的数量为Z；滚动体受力方向与内外滚道垂直线的夹角α；内圈滚道旋转频率为fi；外圈滚道旋转频率为fo。

图4 滚动轴承的典型结构示意图

在此实际采用的轴承各项参数为，滚动体外圈直径77.48 mm，内圈直径52.52 mm，共有8个滚珠体，滚动体与两侧滚道的接触角相等且均是零，即α=0，初始速度以及加速度全部为0，质量约为0.56 kg。

在确定轴承相关参数定义之后，后文针对故障特征频率的理论计算，需要满足以下假设：(1)滚动体在内外环都是呈滚动运动无任何相对滑动；(2)整个轴承在运动过程中呈理想刚体状态，受径向、轴向载荷时不会出现任何形变。

包络分析技术是在故障诊断方向中非常有效的信号分析技术。这种技术最早也叫做高频共振技术，是在20世纪70年代由Mechanical Technology公司提出。其主要是通过采取了有效的共振频率区，经过滤波以及各种变换，最终得到含有故障频率的低频信号，此时只要通过对于这种信号的频谱分析就能很快得出故障。由于这种技术的准确性和高效性，很快就得到人们的广泛使用。

在轴承工作时，各滚珠受载情况其实各不相同，滚珠在转动时，达到最底部的滚珠会承载离心力和轴自身压力的合力，而到达最上面的滚珠则会使得两力相减。此时如果轴承内外环表面出现点蚀故障，那么滚珠在与故障点接触时会发生一定的碰撞从而产生冲击，这类冲击较之正常工作是所受到的振动不同，其一持续时间较短，只会发生在接触瞬间，其二频谱范围较宽，其可以导致轴承其他部分共振情况。当故障点蚀出现之后，轴承在匀速工作时，滚珠不停转动，势必会导致出现周期性经过故障点，从而产生周期性共振，当然不同类型的故障会对应不同类型的周期值，可以通过探测对比所得周期，从而推出轴承的具体故障类型，这也是包络分析技术的基本工作原理[22]。

2 特征频率计算公式

图5给出的是一个典型的滚动轴承。与轴承故障特征频率相关的几何参数都标示在图上。参考相关文章[22]可得出具体计算公式。

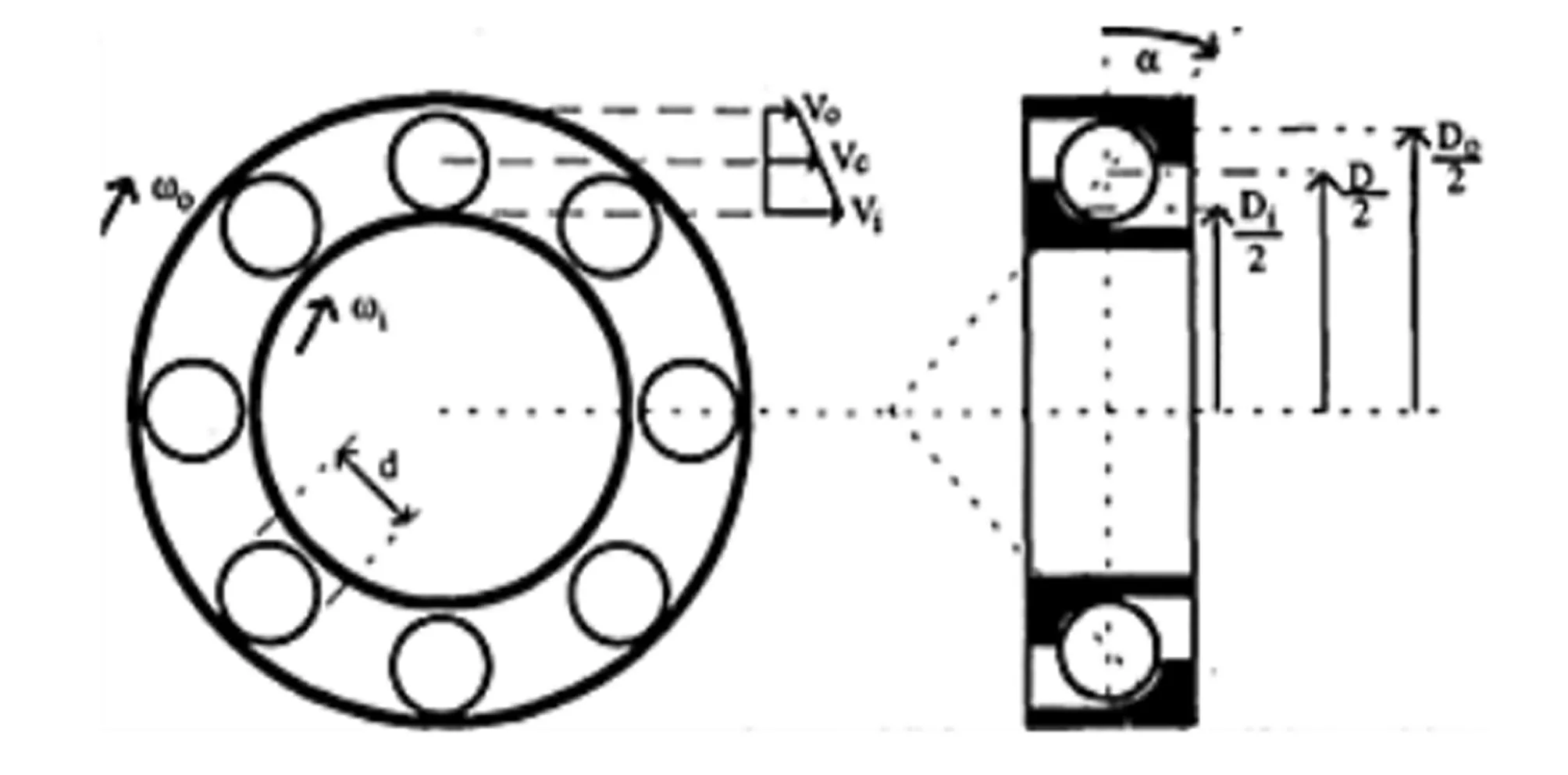
图5 典型滚动轴承及几何参数

滚子中心对应的轴承直径称为轴承中径。根据上图中给出的几何关系，可知轴承中径等于：

(1)

Di表示为轴承内圈滚道的直径，Do表示为轴承外圈滚道的直径。这两个直径与轴承中径的关系可以写为：

Di=D-dcosα

Do=D+dcosα(2)

其中：d为轴承滚子的直径。内外滚道的旋转线速度可以写为：

(3)

式中，ωi为内滚道的旋转角速度，ωO为外滚道的旋转角速度。

假如滚子在滚道上为理想的滚动，那么保持架的旋转速度为内外圈旋转速度的平均值。

(4)

用频率表示的话，则为：

(5)

通常情况下，轴承的外圈是固定不动的。那么上面式子可以简化为：

(6)

保持架相对于内圈的滚动频率可以写为：

(7)

如果轴承有Z个滚子，那么保持架相对内圈滚动一周时，滚子会通过内圈固定点Z次。那么滚子通过内圈固定点的通过频率为：

(8)

当外圈保持固定时，简化为：

(9)

保持架相对外圈的旋转频率可以类似计算：

(10)

类似的，滚子通过外圈固定点的通过频率为：

(11)

滚子的自旋频率可以写为：

(12)

上面这些特征频率都是在假设滚子在内外滚道上没有相对滑动的前提下计算出来的。然而在实际的工程中，以及动力学仿真的情况下，很难达到这个要求，滚子或多或少存相对滚道产生的滑动。因此，实际测量得到的特征频率与理论计算值会有一些误差，需要针对实际情况在一定的误差范围内进行修改。

3 轴承内故障结果与分析

考虑到在四秒落塔实验中，实验舱会出现加速上升到匀速上升最后到自由落体的一个过程，那么实验舱的速度会处于一个变化的过程。在此，动力学仿真中将这个变速的过程等效简化成很多段的匀速过程，通过不同速度下轴承的仿真曲线得出具体的运动轨迹，从而合理的推出在不同速度下运动的情况。同时，对于轴承受载能力也是一个需要验证的方面，在不同受载情况下不同压力对于故障结果的影响也是需要考虑的因素之一。当然在实验舱运动过程中故障点故障程度已经故障部位也都是需要考虑对比的，下面将一一给出实验仿真结果图并进行分析。

首先我们采用了在0.1 s仿真时间，步长为8×10-5，一共采集1 250个数据。根据实际运动状态我们设置的单个轴承承载压力为5 000 N，转速为240 r/s。

3.1 不同速度对比

在实验舱运动过程中会有加速上升到匀速运动的过程以及后续的自由落体运动，这些运动中轴承的速度不是一直不变的，所以针对这种情况，在考虑到算力的情况下决定采用，将不同的速度运动结果进行对比仿真。将加速的过程看成在无数个匀速运动的组合，最终通过两个不同速度的仿真结果进行推广。在给定的初始条件下我们得到仿真结果如图6、7所示。

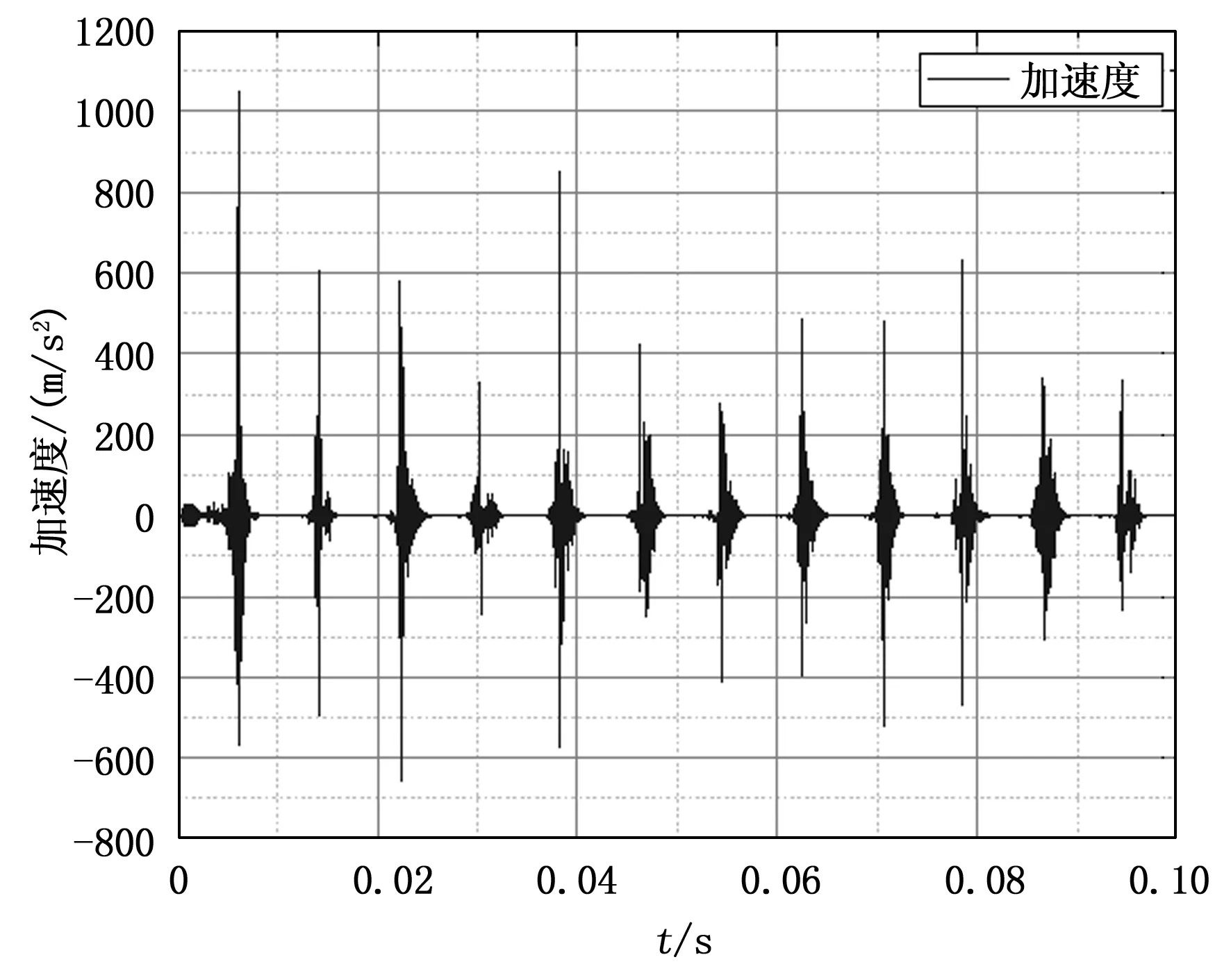
图6 外圈故障点处加速度曲线

通过上文论述到的理论计算公式以及轴承的实际数据我们可以得出滚子通过外圈固定点的通过频率为：

123.45Hz

即在理论计算中滚子通过故障点的频率为123.45 Hz。图中在仿真波形中0.1 s的仿真时间内共出现了12次波峰，该结果也是符合理论计算结果的，后续还会通过包络分析方式计算出仿真结果与理论计算的具体误差为多少。

通过图6和图7可以得出对于故障产生的冲击，在仿真结果上故障点上效果会更明显，噪音更少，在非故障点处受到的冲击远远小于故障点处。但是外圈上的任一点都符合理论计算的结果，后续重点考虑故障点处的仿真曲线。考虑到干扰原因可能为振动冲击的叠加以及共振现象等等导致远离故障点出的外圈加速度效果不如故障点处。

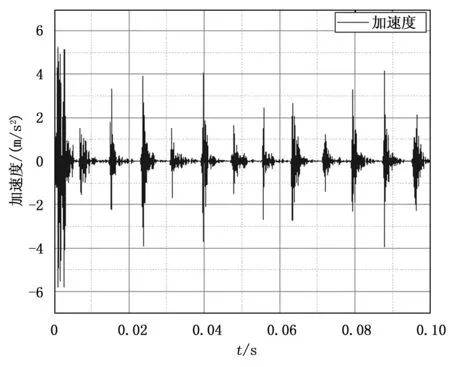
图7 外圈非故障点处加速度曲线

将图6数据进行包络分析，得到的包络谱图如图8所示，同时也对比一下直接将原始数据进行傅里叶变换的结果图9所示。

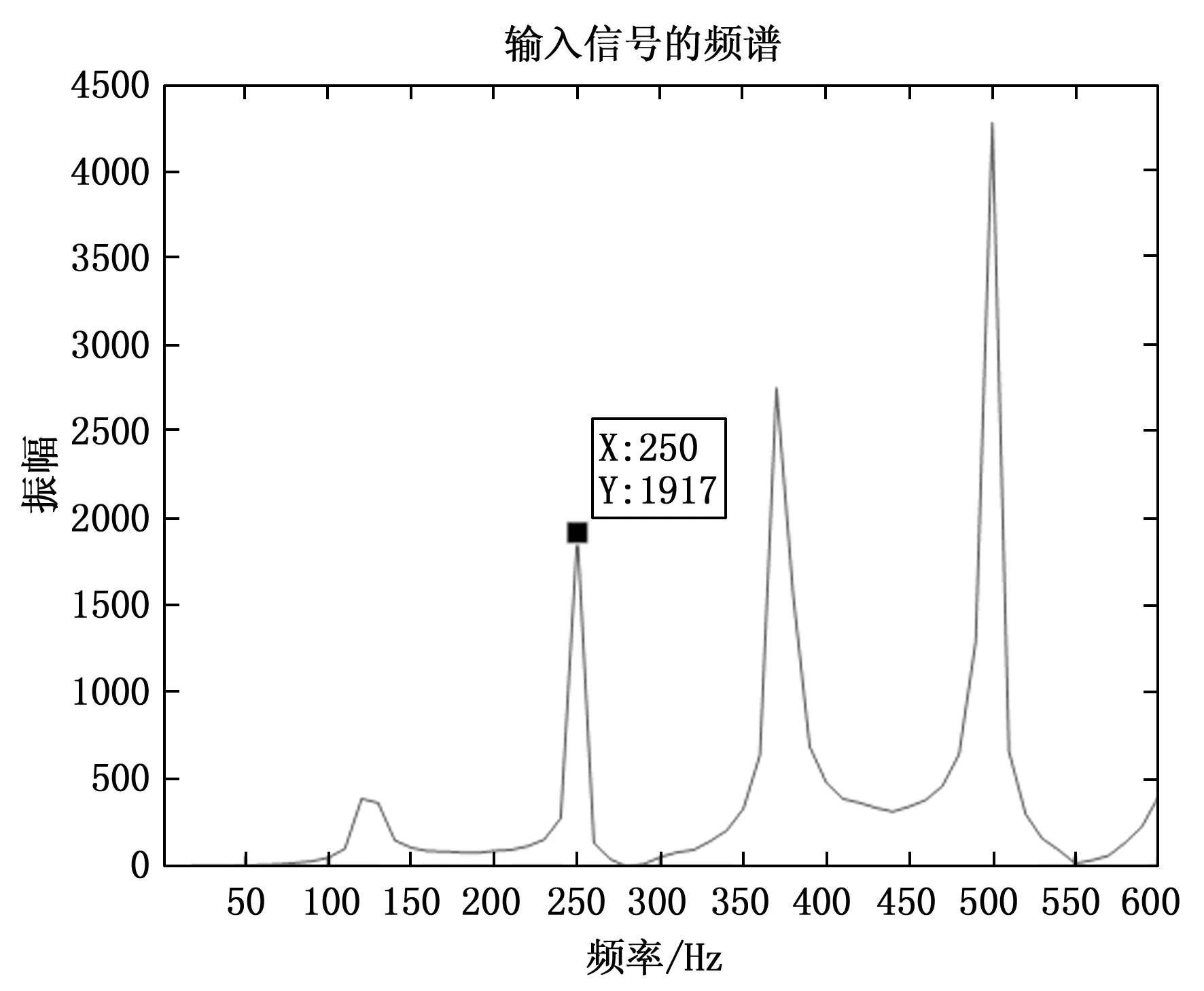
图8 包络谱图

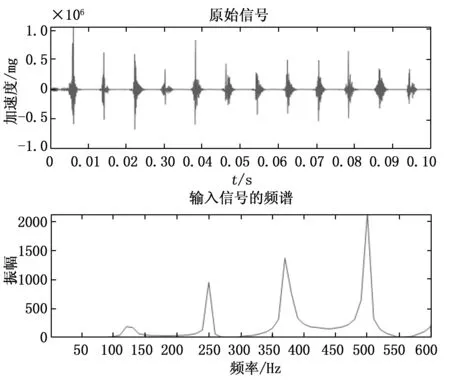
图9 原始信号的直接傅里叶变换

图8和图9结果一致吻合理论预期，同时在240 r/s的转速情况下两个周期频率为250，平均每个周期频率为125，在240 r/s经过理论计算出的结果为123.45 Hz，误差为1%。符合工程上的误差允许范围之内。

模拟实验舱导轨副在加速之后进入更高速的运动状况，将滚轮转速从240 r/s，改成为360 r/s。其仿真结果如图10所示。

图10 外圈故障点处加速度曲线

将所得图10和图6进行对比可以发现，转速为360 r/s的时候经过故障点的平均冲击幅值更大一些约为1.6倍和转速差的1.5倍。故可以大胆猜测，转速倍数约等于幅值倍数，更快的转速导致更快的冲击也会加速轴承的损坏。

利用理论计算公式可以得出理论计算值，也符合在0.1秒的时间内出现了18次波形的结果。接下来通过图11包络图计算出具体误差值。

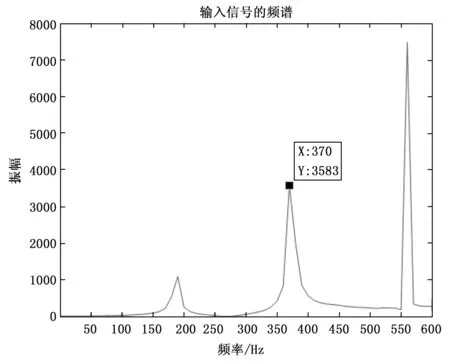
图11 360 r/s数据的包络谱

通过图11所示，360 r/s转速的情况下的包络分析图仿真频率两个周期为370，平均每个为185和理论计算出的185.18 Hz误差频率为0.1%。完全符合工程上的误差允许范围之内。

3.2 不同载荷对比

模拟实验舱实际运行过程中，如遇到振动情况将会导致不同轴承的受载情况也不一样，且不同实验舱的重量也不一样，故在加速到360 r/s的基础上继续进行调整，将单个轴承的5 000 N受载力加大到了8 000 N，通过仿真对比结果如图12所示。

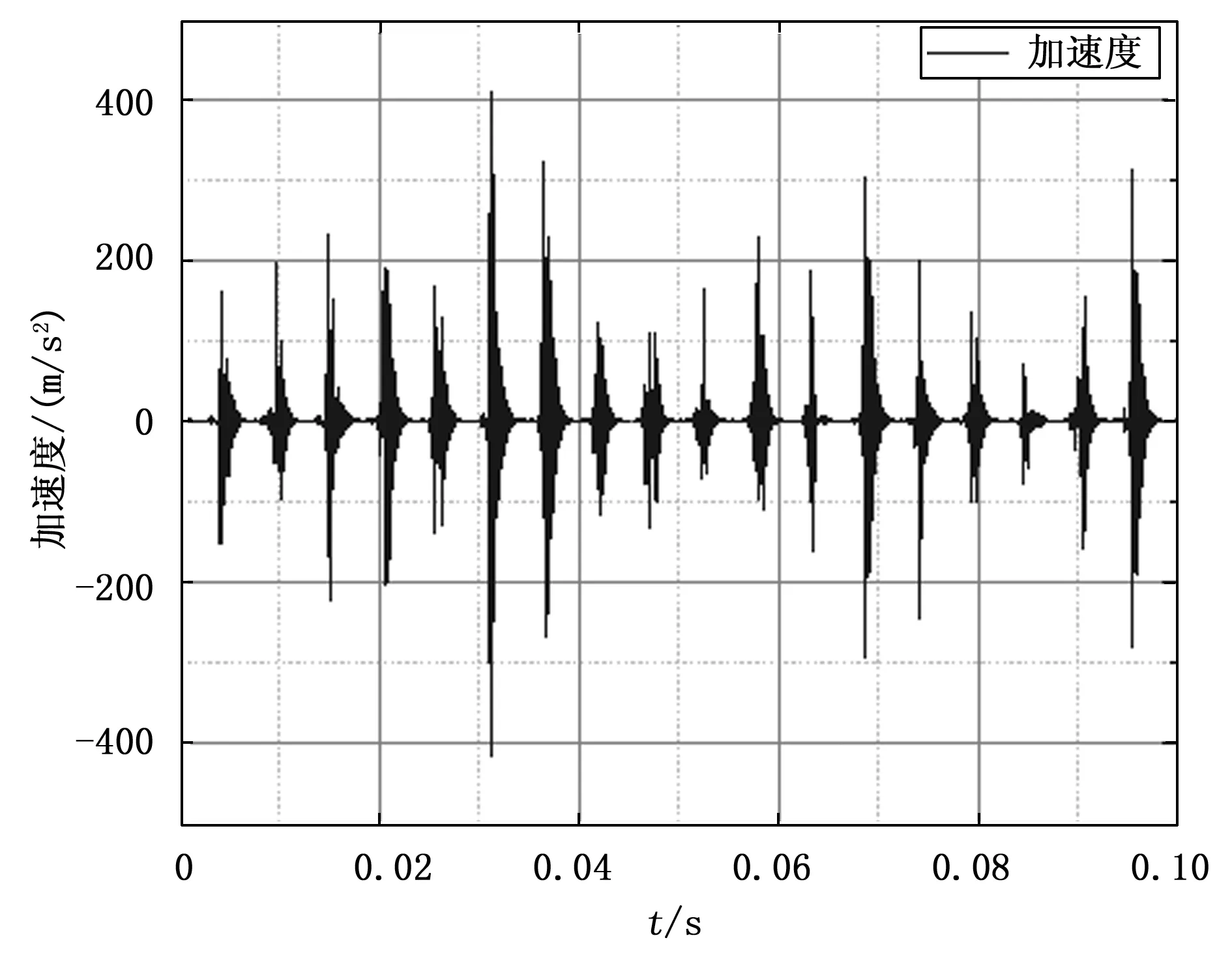
图12 外圈故障点处加速度曲线

将图12与图10进行对比可以看出幅值变小，在相同速度的情况下，受载力大的情况下仿真结果平均幅值变小，分析结果可能原因为受载力较大，改变物体运动状态变难，所以晃动幅度变小。在受载力变大的情况下并没有改变转速故由公式看的出理论频率并不会变化仍然是185.18 Hz，同时在该仿真结果图中0.1 s时间内出现的18次波峰为符合预期，通过包络谱图13计算出具体误差值。

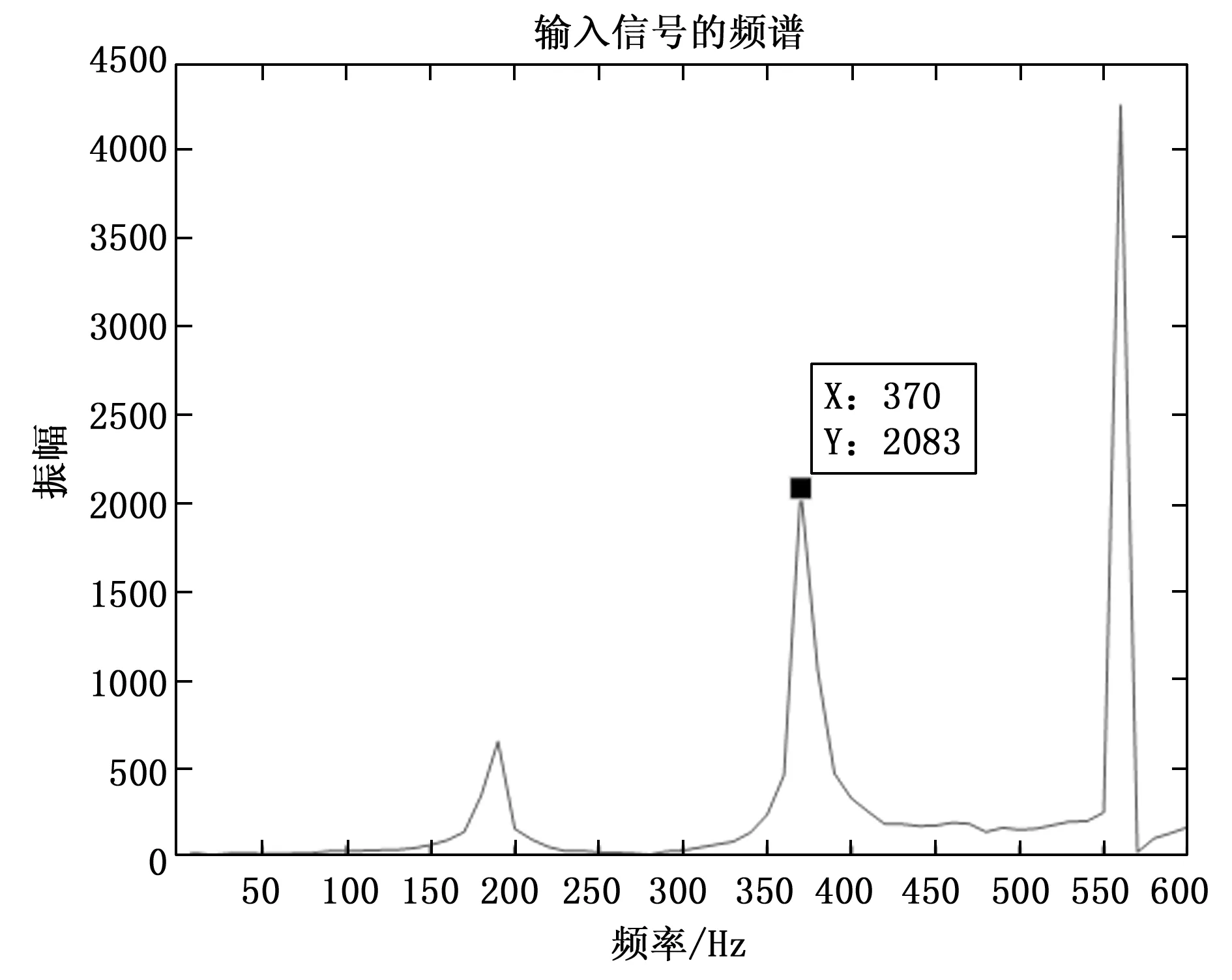
图13 包络谱图

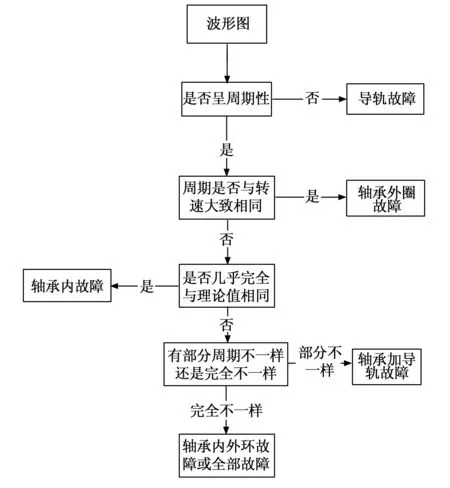
图14 流程图

通过图13和图11的比较也可以看的出，在幅值上受载力大幅值变小，同时频率没有变化，两次周期的频率为370，与理论值的误差仍然为0.1%。

4 导轨副整体故障结果与分析

前文已经阐明在整个导轨副中，轴承部件是最容易出现故障的部件，在详细要讨论完轴承部件的各种故障结果，仍然不能忽视整个导轨副部件其他部件故障对于数据的影响。经调研，大致可以考虑到轴承外部在导轨上的压溃现象以及导轨上多次摩擦造成的划痕。将整个模型简化建模仿真，考虑到如果在导轨上出现故障，对于整个轴承滚动是单一性的故障扰动，如果出现在轴承上，那么扰动是呈周期性出现，具体仿真结果如下。

4.1 初始条件下导轨出现划痕

在240 r/s的转速载荷为5 000 N的情况下，单独导轨上出现单处故障可以较明显看到在遇到划痕处轴承上会有明显的加速度冲击变化。同时可以合理推断出如果出现多处且无周期性的冲击时，为导轨上出现多处故障。

对于出现明显冲击加速度的情况，将该扰动叠加到轴承外圈故障数据中，整体上依旧会符合外环故障的理论值，但是在某一个周期内出现偏差是因为在该周期内遇到导轨上的划痕造成的影响。

4.2 初始条件下轴承外部出现划痕

该情况，前期整个导轨副轴承刚开始运动处于不稳定的状态在稳定之后基本上是呈周期变化，将稳定之后的数据经过计算可以得出和240 r/s转速一致的振动周期。且随着仿真的时间变长，扰动效应叠加之后愈发严重。可以通过仿真结果看出如果出现不符合内外环理论值但符合轴承转动周期的冲击加速度考虑可能为外环与导轨滚动出现的故障。

外环和轨道滚动摩擦中，外环出现故障对于轴承内部故障数据影响较大，但是对于工程上定位故障处于轴承或导轨上无影响。将外圈故障注入到轴承内部故障的情况，数据进行叠加之后可以看出对于整个数据影响较大，整个周期都会发生变化，和理论计算值差异较大，此时可以考虑到是否为轴承内部和外部都出现了故障。

4.3 故障类型判断小结及流程图

外部扰动故障虽然对于内部轴承判断有较大的扰动，但依然不影响对于故障的分析，还可以通过数据大致分析出是否为几个故障的组合，对于工程上只需要定位出可能出现的故障的部件，并进行一定的检修，有实际工程作用。

具体判断方式可以通过如图15的流程图看出判断步骤。在得到加速度波形之后快速做出定位。

首先考虑是否有周期性，若无周期性必然是导轨故障且可知是导轨表面出现故障；若出现周期再判断周期是否与转速基本一致，若一致可判断为轴承外圈出现故障；若不一致在去判断是否与理论计算值一致，如果符合则为轴承故障，如果部分符合部分不符合则考虑到是轴承加导轨故障；如果是完全不一样的那么考虑可能是轴承内外部都出现故障或全体出现故障。

5 结束语

本文通过建立具体模型，将实验舱导轨副最易出现问题的轴承部件进行单独研究，深入讨论了在不同运动状态下的滚动体故障情况，根据滚动体理论计算的故障频率特征和实际仿真的结果进行计算对比，验证了实验仿真的正确性。同时也考虑到整个导轨副其他可能的故障的影响，将整个导轨副的故障判断方法列举出来。可以通过仿真得到如下结果：

1)同载荷不同速度情况下，速度越快受到的冲击加速度越大，可以大致推算出不同速度情况下的故障曲线；

2)同速度不同载荷的情况下，载荷越大故障点受到的冲击加速度也会越大；

3)结合到整体导轨副上，当轨道出现故障时，会有不呈周期性的冲击力变化；出现在轴承外部和导轨副的压溃会有周期性的冲击力变化。由此也可以检测出单独导轨或者轴承外部故障的情况，同时结合到整体上判断故障时，对比理论计算结果可以大致分析是否有多处故障的可能。

4)综合以上仿真结果与理论结果的验证，本文提供的方法在模拟轴承在实验舱导轨副中不同的运状态下结果准确，不同于之前大都采用了凯斯西储大学的轴承数据去进行验证。我们不仅将不同类型的轴承计算结果进行对比，同时在整个导轨副上的其他故障讨论，具有一定的工程价值，也进一步完善了导轨副故障分析的理论基础，为后续深入研究打下一定的基础。

下一步工作计划考虑与人工智能结合，可能会面临大量数据的需要，会完善数据的采集方式，不仅仅依赖于仿真得到实验数据，同时将实验台得到实验数据结合起来。所得数据全部和人工智能结合起来，尝试加入神经网络的集合实现故障结果的判断和识别，探索神经网络的加入能否带来更快更准确的故障类型的判断从而减少人工的加入。最终可以成功应用在实验舱的运行数据处理且完成具体故障的定位，是极具实际工程作用的一个探索研究。