基于ARIMA-LSTM的高速公路交通安全组合预测模型研究
2023-06-02梁乃兴杨文臣曹源文
梁乃兴,闫 杰,杨文臣,曹源文,房 锐
(1. 重庆交通大学 土木工程学院,重庆400074;2. 云南省交通规划设计研究院有限公司 陆地交通气象灾害防治技术国家工程实验室,云南 昆明 6502001;3. 重庆交通大学 交通装备与系统集成重庆市重点实验室,重庆400074)
0 引 言
全球每年大约有124万人死于交通事故,超过2 000万人因事故受伤,若以此趋势,2030年道路交通事故或将成为全球第7大死亡原因[1]。此外,高速公路的百公里事故率、百公里伤、亡率与普通公路相比将增加2.0倍、2.8倍、4.0倍[2]。因此,探索高速公路交通事故在时间维度上的分布规律,并建立具备良好预测能力的高速公路交通事故预测模型,主动研判交通事故态势及源头治理对策,一直是宏观道路交通安全管理的重要问题。
道路交通事故预测已经从传统的定性预测发展为定量预测,定量预测的模式又可分为基于因果关系和基于时空关系建模2种[3]。因果模型主要基于道路几何特征、道路基础设施、交通环境(交通量、大型车比例等)等影响因素与交通事故评价指标之间的逻辑关系进行建模,其代表性预测方法为逻辑回归分析法。时空模型主要基于交通事故在时空维度上的分布规律进行建模,通过捕捉历史事故数据中的时空特征规律,进行外延预测和安全调控。多数学者对交通事故因果关系模型进行了大量的研究,而对于高速公路时序交通事故预测研究相对较少,其主要预测方法包括时间序列法、马尔科夫法、神经网络法等。
经典的时间序列统计回归模型最早应用于交通事故时空模型,J.KARTIKEYA等[4]对比分析了多种时间序列模型在印度交通工程中的应用及其局限性;张杰等[5]基于1970—1997年全国交通事故10万人口死亡率数据建立自回归差分移动平均(ARIMA)模型,该模型能较好拟合交通事故数据并具备良好的短期预测能力;C.CHUKWUTOO等[1]基于ARIMA与ARIMAX(带回归项的ARIMA)模型对尼日利亚阿南布拉州的道路交通事故进行了预测,表明引入外部变量的ARIMAX模型优于ARIMA模型;黄宇等[6]通过建立向量自回归(VAR)模型对交通事故与经济损失之间的关系进行了研究。经典时间序列模型大多建立在众多前提与假设之上,实际应用中很多目标事件并不能完全满足这些假设,限制了经典时序模型的预测效果。
近年来,系统工程和机器学习理论模型逐渐应用于交通事故时间序列预测。吴卢荣[7]运用聚类分析与马尔科夫链建立了宏观交通安全预测模型,预测了未来31个地区的交通安全趋势;陈玉飞等[8]基于交通事故数据,建立了灰色关联模型(GM),结果表明GM(1,5)模型优于GM(1,8);蒋艳辉[9]建立了基于指数平滑和马尔科夫链的交通事故预测模型,用以预测交通事故造成的死亡人数;张志豪等[10]利用1997—2016年交通事故统计数据,分别建立了多元线性回归、BP及LSTM神经网络,发现LSTM模型预测结果最好。
为提高交通事故单一时序模型的预测精度,许多学者提出组合预测的方法。X.H.JIN等[11]建立了灰色马尔科夫组合预测模型,其相对误差低于灰色预测模型;G.REN等[12]等基于粒子群算法与SVR建立了事故预测模型,其结果优于BP模型;谢学斌等[13]基于ARIMA及XGBoost算法建立了组合预测模型,用于拟合1973—2010年全国交通事故统计数据;Z.H.ZHANG等[14]以1997—2016年全国交通事故死亡人数为基础,建立了基于LSTM和梯度提升回归树(GBRT)的事故组合模型。研究表明,与单一模型相比,组合模型的预测能力和鲁棒性均有所提升,是目前时序交通事故预测的主要方向。
LSTM神经网络能够有效逼近时序数据的不确定性和周期性,已在金融、交通流等多个领域取得好的应用效果,但其对样本数据量要求较高。ARIMA模型可以较好拟合线性时序特征,提供先验知识,但对非线性特征的捕捉能力弱,目前鲜有将ARIMA和LSTM组合并应用于交通事故预测方面的成果。因此,研究以重庆市11条高速公路交通事故数据为研究对象,分析交通事故总数和死亡人数的月分布规律,通过ARIMA时序统计模型和LSTM神经网络分别拟合时序交通事故数据的线性和非线性特征,构建山区高速公路交通事故ARIMA-LSTM组合预测模型,可为高速公路主动交通安全管理和综合治理提供参考。
1 方法模型
1.1 ARIMA模型
ARIMA (p,d,q) 模型是应用最为广泛的一种时间序列预测方法[15],模型建立后可根据历史值和当前值来预测未来值。基本建模流程为:首先检验时间序列平稳性,通过差分对非平稳序列进行平稳化处理,确定差分参数(d);其次通过观察偏自相关(PACF)和自相关图(ACF)确定自回归参数(p)和移动平均参数(q),以此建立模型,如式(1)[16]:
(1)
式中:Φ(·)、Θ(·)分别代表p阶自回归系数多项式、q阶移动平均系数多项式;d=(1-B)d为差分计算;B为延迟算子,且Bnxt=xt-n;{εt}为随机误差序列;E(·)、Var(·)分别为·的期望与方差。
1.2 LSTM模型
LSTM神经网络是递归神经网络(RNN)的一个变种,LSTM神经元的独特结构很好的解决了长期依赖(时间步长很大)情况下,传统RNN模型的梯度消失或爆炸等问题,使神经网络模型具备传递较远节点历史信息的能力[17]。LSTM通过在递归神经网络神经元结构中增添遗忘门、输入门以及输出门,不断调整自循环中的的权重,当参数固定时,各时点的积分尺度可以动态浮动,从而规避梯度消失或爆炸问题,其示意如图1[18]。
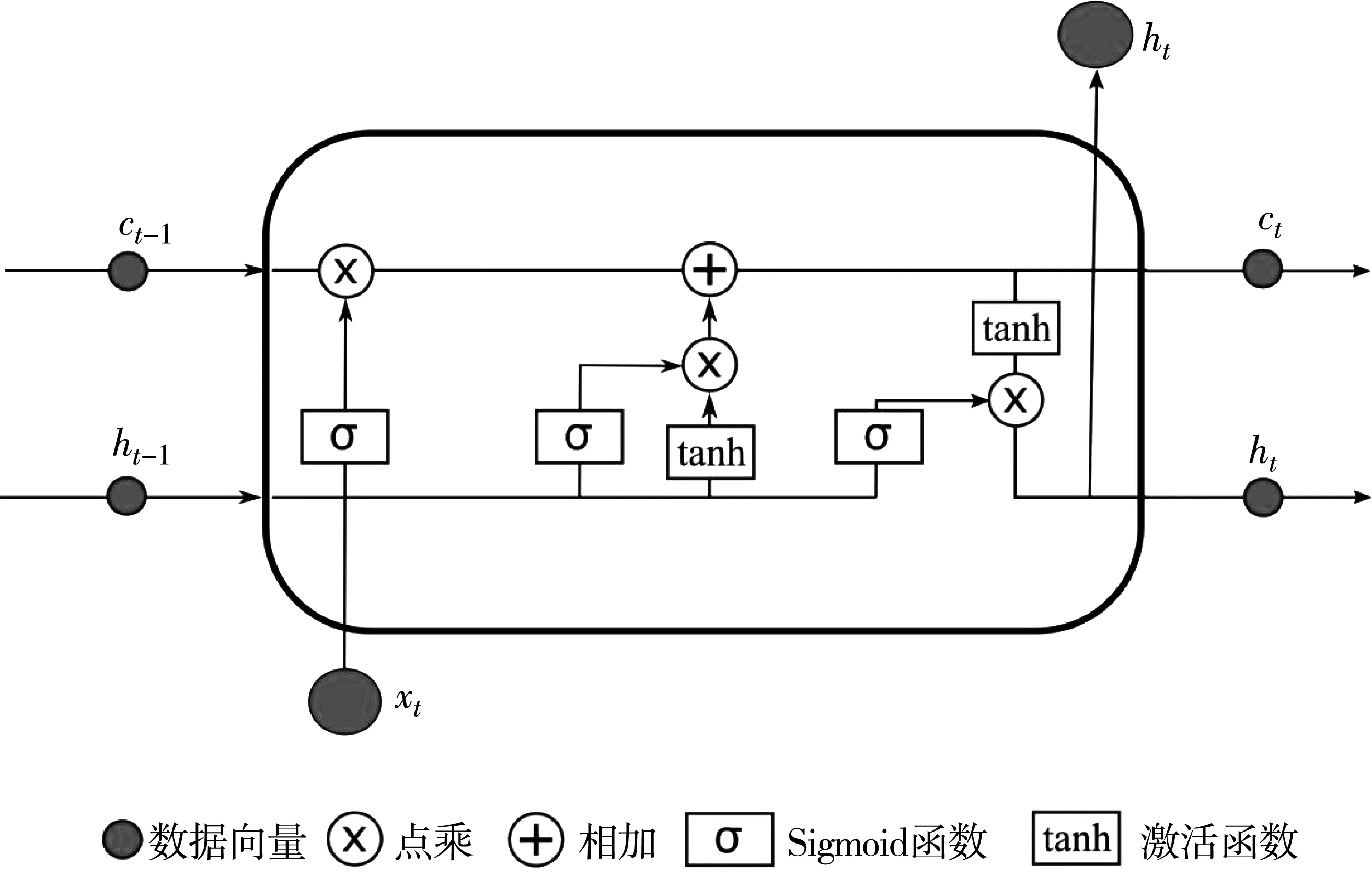
图1 LSTM神经网络示意Fig.1 Schematic diagram of LSTM neural network
假定时间步长为T′,LSTM神经网络的输入序列为X={x1,x2,…,xt,…,xT′}。图1中xt为t时刻神经元的输入,ht-1为上一神经元的输出,ct-1为截止到上一时刻的神经元状态。LSTM神经网络基本公式如式(2)~式(6)[19]:
ft=σ(Wf×[ht-1,xt]+bf)
(2)
it=σ(Wi·[ht-1,xt]+bi)
(3)
(4)
ot=σ(Wo·[ht-1,xt]+bo)
(5)
ht=ot×tanh(Ct)
(6)
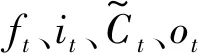
以t时刻为例,LSTM神经网络首先通过遗忘门处理传入t时刻的神经元状态ct-1,舍弃无效信息,如式(2);然后通过式(3)、式(4)建立输入门,根据上一时刻的输出与当前时刻的输入将神经元状态更新为Ct。最后通过输出门输出Ct中的相关信息,此功能的实现如式(5)、式(6)。
1.3 ARIMA-LSTM组合模型
道路交通事故数据沿时间维度的分布既包含线性特征又包含非线性特征。ARIMA模型隶属线性模型,只能拟合时间序列数据中的线性特征, LSTM神经网络则可以弥补这一缺点[20]。先采用ARIMA模型对交通事故数据中的线形特征进行拟合预测,然后采用LSTM神经网络模型对残差序列中的非线性特征进行拟合,最后将二者进行线形组合得到组合模型最终值。具体建模步骤如下:
1) 整合、处理高速公路交通事故数据,将事故数据延时间维度展开,以单位根(ADF)法检验各序列的平稳性,采用差分、平滑等方法将非平稳序列转为平稳序列。

(7)
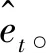

(8)
2 数据选取
2.1 数据来源
将重庆市包茂高速等11条高速公路2011—2016年共计65 131起交通事故数据为研究对象,由于事故数据不完整,将不完整的高速事故记录剔除后,共使用65 119起交通事故数据用于构建交通事故月分布序列,事故统计信息如表1。将2016年8月1日前的序列数据作为模型的训练集,将2016年8月1日及之后时刻的序列数据作为模型的测试集,训练集样本量约占全集的93%,测试集约占比7%。

表1 2011—2016年11条高速公路交通事故统计
2.2 指标选取
道路交通事故的总量指标主要包括事故数量、死亡人数、受伤人数和财产损失4项。由于数据原因仅采用事故数量和死亡人数2项指标,时间以“月”为单位,将高速公路交通事故数据按各指标在时间维度展开,见图2、图3。
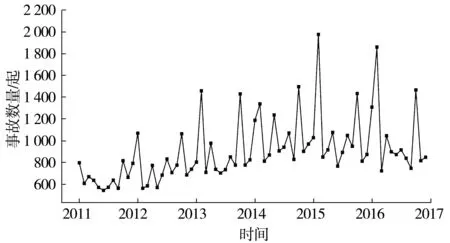
图2 “事故数量”初始序列分布Fig.2 Initial sequence distribution of “number of accidents”

图3 “死亡人数”初始序列分布Fig.3 Initial sequence distribution of “death toll”
此外,以均方根误差(RMSE)以及平均绝对百分比误差(MAPE)作为评价模型优劣的衡量指标。如式(9)、式(10):
(9)
(10)
式中:Ttotal为样本总量,即总时间步长;ERMSE为均方根误差;EMAPE为平均绝对百分比误差。
3 实例分析
3.1 数据处理
ARIMA时间序列模型要求序列数据为平稳序列,因此建模之前首先检验序列数据的平稳性。采用ADF法分别检验“事故数量”与“死亡人数”初始序列,如表2。由表2可以看出“事故数量”初始序列的P值 >0.05且T值大于3个置信区间的临界值,故“事故数量”序列为非平稳序列,该序列需要进一步平稳化处理。而“死亡人数”初始序列P值 <0.05,为平稳时间序列。

表2 初始序列ADF检验
由图2可以看出“事故数量”初始序列振动幅度较大且呈“年”周期性变化。首先对该序列进行对数转换,以减小序列数据的振动幅度;之后运用滑动窗口为12的移动平均方法剔除序列中的周期性因素;最后采用差分法将序列处理成为平稳时间序列,过程中分别采用ADF检验序列的平稳性,结果如表3。
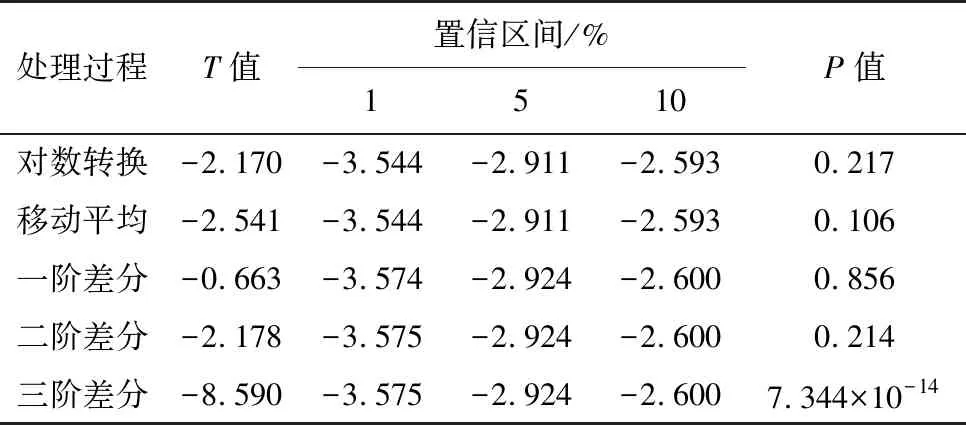
表3 “事故数量”序列ADF检验
3.2 ARIMA模型建立
通过处理后的平稳时间序列生成的偏自相关图(PACF)与自相关图(ACF)对ARIMA模型进行参数估计,如图4、图5,图中灰色区域为置信区间。

图4 “事故数量”序列的ACF与PACFFig.4 ACF and PACF diagrams of the “number of accidents” sequence

图5 “死亡人数”序列的ACF与PACFFig.5 ACF and PACF diagrams of the “death toll” sequence
以“死亡人数”序列为例,其自相关系数为2阶截尾,偏自相关图呈拖尾状况。故模型参数可以估计为ARIMA(0, 0, 2)、ARIMA(1, 0, 2)、ARIMA(1, 0, 1),3个模型进行试算后求出AIC值,分别为465.38、461.85、462.17。依据最小信息量原则,“死亡人数”指标的最佳模型为ARIMA(1, 0, 2)。同理,“事故数量”指标的最佳模型为ARIMA(1, 3, 2)。
“事故数量”和“死亡人数”序列的ARIMA模型预测结果如图6,图中竖直虚线用以区分样本集,虚线左侧为训练集样本,右侧为测试集样本。此外模型建立后还需要对模型的残差序列进行正态性和自相关性检验,以确保模型的有效性。由图7的正态性检验可以看出,残差序列基本服从正态分布;同时对残差进行D-W检验,“事故数量”模型的D-W检验值为2.31,“死亡人数”模型的D-W检验值为1.99。两者的D-W检验值都接近2,模型满足自相关检验。

图6 “事故数量”和“死亡人数”ARIMA模型预测Fig.6 “Number of accidents” and “death toll” ARIMA model prediction

图7 残差QQ图Fig.7 Residual QQ plot
由图6可知,“事故数量”ARIMA模型的预测效果良好,比较接近初始序列数据的分布曲线,并能够预测出该序列测试集数据的变化趋势;“死亡人数”ARIMA模型对原始序列的拟合预测效果一般,存在一定的滞后性,并且随着时间步长的增长,模型对于测试集的预测能力逐渐下降,无法准确预测出测试集的变化趋势。
3.3 LSTM模型建立
基于Pytorch 1.7.1搭建LSTM神经网络,分别根据“事故数量”和“死亡人数”ARIMA模型的残差序列建立LSTM预测模型,旨在通过拟合训练集中残差序列的非线性时序特征,对测试集中的残差进行预测,使组合模型获得更优的预测效果。残差序列的训练集与测试集划分同样采用上述时间节点,以“死亡人数”LSTM模型为例,具体建模流程为:
1) 对序列进行归一化,将数据压缩到 [-1,1] 范围内,以确保LSTM模型能够快速收敛;
2) 对模型进行超参数选择,经过反复对比发现,当残差序列的时间步长为4时模型能很好地捕捉残差序列中的非线性因素。经过反复调整,最终超参数选择为:Adam优化器、学习率为0.001、batch_size = 1、神经网络层数为1、神经元个数为45、迭代次数为140;
3) 最终模型输出结果需要反归一化,对数据进行还原。
模型预测结果如图8,可以看出LSTM神经网络模型能够从残差序列中提取一定的有效时序信息。
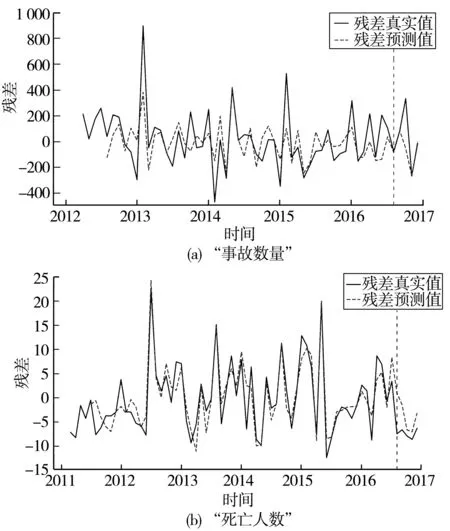
图8 “事故数量”和“死亡人数”LSTM残差预测Fig.8 “Number of accidents” and “death toll” LSTM residual prediction
3.4 ARIMA-LSTM组合模型建立
将ARIMA预测值与LSTM得到的残差预测值依据式(8)进行线性组合,得到最终的组合模型预测值。“事故数量”和“死亡人数”指标的初始序列、ARIMA模型预测值以及组合模型预测值对比分析(图9)。图9中两个指标的组合模型相较于单一的ARIMA模型都有很大的提升,更接近原始序列,并且组合模型能够更好拟合预测出序列中的趋势变化。然而,在每年2月和10月的事故数量和死亡人数峰值月份,组合模型的预测误差仍较大,这是因为在春运和国庆节重大假日,这2个月的交通流量激增,交通事故的发生更为集中,加之研究节假日的样本数量少,所构建的组合模型尚不能有效逼近事故数据的非时序特征所致。

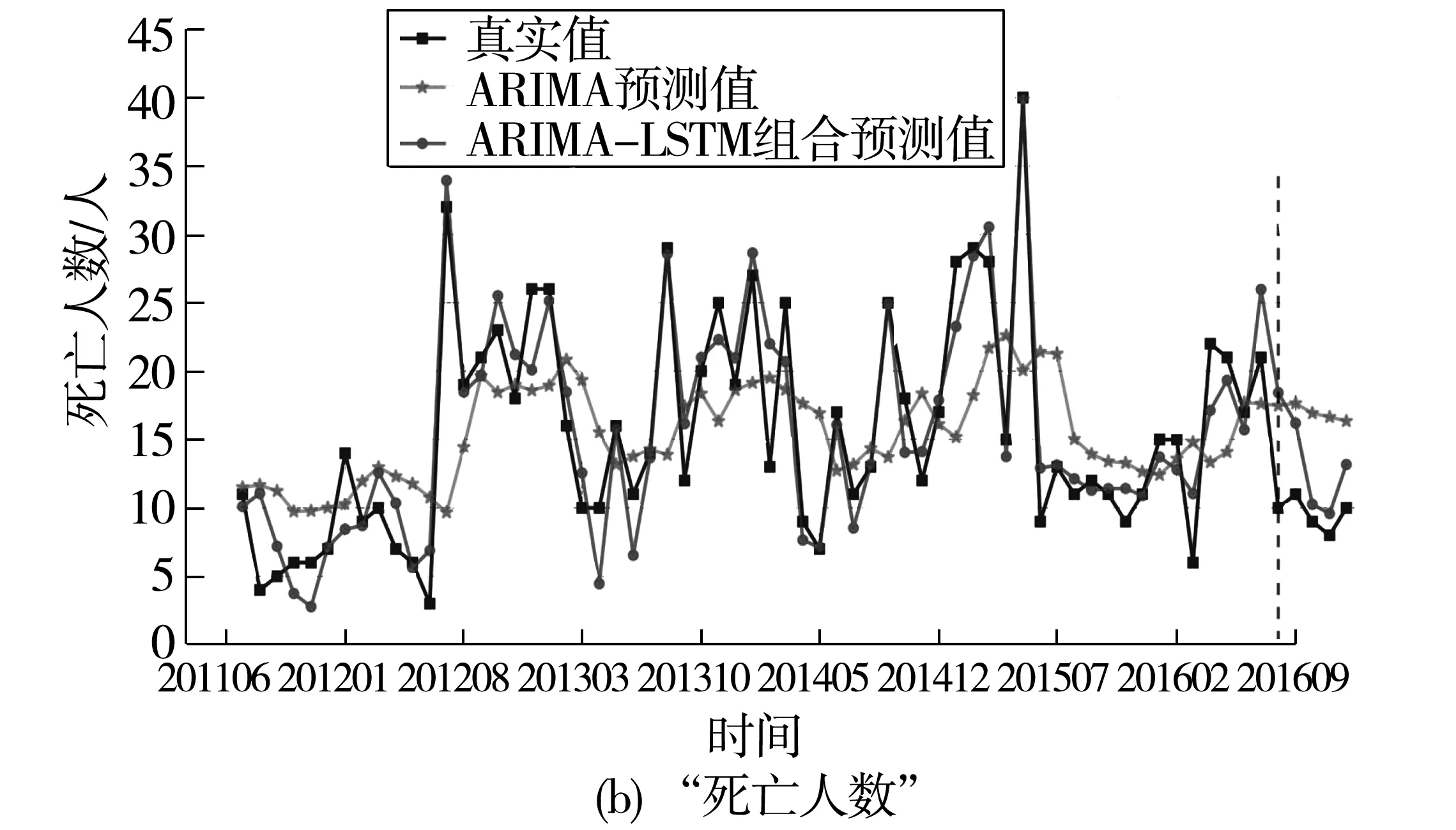
图9 “事故数量”和“死亡人数”各模型预测结果对比Fig.9 Comparison of the predicted results between models of “Number of accidents” and “death toll”
采用RMSE以及MAPE来衡量模型的预测效果,如表4。可以看出组合预测模型的各项指标更优,以“死亡人数”组合预测模型改善最为显著,其 ARIMA-LSTM组合模型与ARIMA模型相比,RMSE与MAPE分别降低了4.02与27.99%,即相较于单一模型,组合模型的RMSE和MAPE分别改善了55.83%和54.80%;“事故数量”的ARIMA-LSTM组合预测模型的RMSE和MAPE相较于ARIMA模型分别降低了51.91与3.71%,组合模型的RMSE和MAPE分别改善了23.15%、23.29%。

表4 模型评价Table 4 Model evaluation
4 结 论
1)选取事故数量和死亡人数两项指标,建立了基于ARIMA-LSTM的高速公路交通安全时序组合预测模型,通过ARIMA模型可捕捉各项指标时序数据中的线性因素,而LSTM神经网络模型可预测各指标残差序列中的非线性因素。
2)单一的ARIMA模型对“事故数量”序列的预测效果较好,平均绝对百分比误差为15.93%;ARIMA模型对“死亡人数”原始序列的预测精度一般,但总体上能预测出死亡人数的变化趋势。
3)ARIMA-LSTM组合预测模型相较于单一的ARIMA模型在预测能力上有一定程度的提升,能够更好挖掘出时间序列中的有效信息。对于事故数量指标,组合预测模型的RMSE和MAPE相较于ARIMA模型分别改善了23.15%、23.29%;对于死亡人数指标的改善更为显著,与ARIMA模型相比,其组合模型的RMSE和MAPE分别改善了55.83%和54.80%。
