粗集料分布形态对沥青混合料疲劳性能影响研究
2023-06-02吴国雄
吴国雄,姜 勇,张 伟, 陈 灏
(1.重庆交通大学 土木工程学院,重庆 400074;2.重庆建筑工程职业学院 交通与市政工程系,重庆 400072;3.中机中联工程有限公司 市政五所,重庆 400039)
0 引 言
沥青混合料疲劳损伤性能一直是道路研究者关注的重要内容之一。张婧娜等[1]对于不同类型沥青混合料进行了劈裂试验和蠕变试验,建立了一种基于累计流动能耗预测疲劳性能的方程方法;朱洪洲等[2]研究分析了饱和度、空隙率、胶粉比以及沥青膜厚度对疲劳方程中特征参数的影响;杜群乐等[3]利用应力控制模式下疲劳试验对比分析旋转压实与马歇尔击实制备试件方法下不同混合料的疲劳性能,并研究了公称最大粒径对混合料疲劳性能的影响。
在对疲劳性能的研究分析中,国内外的大多数学者都是从实验现象法的角度去寻找规律和探索原理,这种方法虽然有其实用性,但在沥青混合料的内部细观评价方面有较大限制,不能量化评价混合料细观特征对混合料疲劳性能的影响。随着计算机技术的发展,众多学者利用计算机技术实现对沥青混合料内部细观特征的识别量化或者通过软件重构模拟来探索混合料性能与细观特征的关联。E.MASAD等[4]运用数字图像处理技术并结合相关数学方法及程序,定义了一些评价集料自身形态的指标;J.K.ANOCHIN-BOATENG等[5]通过3D激光扫描系统(CSIR)扫描集料信息,并通过计算机模拟软件重构了集料的三维虚拟模型; M.ZEGHAH等[6]利用离散元软件设计了虚拟三轴压缩试验,结果表明试件的回弹模量与其侧向压力存在正向关系性;王荣等[7]利用离散元软件进行了虚拟单轴静态蠕变试验;E.MAHMOUD[8]等通过在离散元软件PFC2D 中设计完成模拟劈裂实验,并将分析计算所得的沥青混合料内部集料细观特性与实验结果对比分析,实现了混合料内部转结构状态、集料细观特征与宏观性能的相互关联。
由上述可知,虽然集料细观特征参数相关研究已有很多,但对沥青混合料疲劳损伤性能影响的研究还比较少。利用数字图像处理技术和离散元软件进行沥青混合料疲劳损伤模拟实验,揭示了粗集料分布形态特征对沥青混合料疲劳性能的影响。
1 疲劳虚拟实验二维细观模型
1.1 粗集料分布形态参数选择
棱角性参数是指沥青混合料中粗集料和细集料颗粒表面的突出程度。美国公路战略研究(SHRP)计划中,将棱角性认为是形状、棱角性和表面纹理3个粗集料自身形态特征中最重要的一个参数。棱角性是通过计算所有边界点的梯度向量角,并将其累计加和而得到的,但由于笔者旨在研究二维平面的棱角性参数,故将梯度向量变化转变为平面斜率向量变化,即可得到粗集料在二维平面的棱角性参数。对于整个沥青混合料的粗集料棱角性参数,计算公式为:
(1)
式中:Ai为单个粗集料的棱角性指标;Ii为集料的面积指标;M为粗集料棱角性加权指标。
对于沥青混合料中集料接触状态研究,魏鸿等[9]建立了表征集料接触特性的量化指标“接触对”。在判定“接触对”时可假设集料颗粒均被沥青胶浆膜覆盖,那么如果2个临近颗粒完全接触,根据图像实际分辨率大小,其颗粒边缘应该相距不超过一个像素。
笔者选择棱角性和接触对这2种细观特征作为粗集料分布形态参数进行研究,并利用数字图像处理技术对集料参数进行提取。
1.2 粗集料分布形态参数提取方法
传统沥青混凝土实验中定义粗集料为最大公称粒径2.36 mm以上的集料。针对本次实验研究集配AC-13,对4.75、9.5、13.2 mm的粗集料进行了前期图像处理,数据显示,将研究粒径定为9.5 mm及13.2 mm时,描述其特性差异更为明显,对比实验更具可行性。
对于棱角性参数,通过相机获取的图像中存在阴影噪声及集料表面的灰质噪音,是无法直接用于提取集料细观特征表征参数的,需要先采用Photoshop对原图像进行效果增强和去阴影处理,然后使用MATLAB对增强后图像进行二值化处理,如图1。根据所得集料轮廓线,运用MATLAB对轮廓上的像素点坐标进行排序,计算获得粗集料棱角性参数和面积参数。

图1 图像二值化处理Fig.1 Image binarization processing
接触对表征集料接触特性的量化指标,利用数字图像处理技术可得到混合料截面二值图,然后使用MATLAB软件内置的腐蚀和膨胀函数处理图像中存在的黏连现象,进而判定集料接触的接触对。黏连现象处理前后二值图效果如图2。为了避免切割试件时产生的不可逆损伤,根据段跃华等[10]研究成果,将试件中部接触点个数相对于顶部和底部的衰减系数定为0.7,这样切割时只用切割顶部和底部,并提取出接触点个数乘以衰减系数。

图2 处理前后截面放大Fig.2 Enlarged cross-section before and after processing
1.3 二维数字试件生成
数值模型的建立与常规方法有所不同,选择将所采集的粗集料图像随机填充进二维截面来构建数值模型。运用概率理论并根据三维体积级配推算出二维数量级配,然后通过MATLAB程序将采集所得粗集料随机投放入截面圆中生成二维马歇尔界面,如图3。由于PFC2D无法识别以矩阵形式存在的图像数据,所以需要先将该图像数据导入CAD中,生成各级料分别建立图层的CAD交互图像,然后通过代码使离散元软件PFC与CAD实现交互,在实现截面圆内离散元颗粒生成及赋值后,即可将CAD图像的颗粒位置数据导入离散元软件中以生成离散元数字试件,如图4。

图3 二维马歇尔界面Fig.3 Two-dimensional Marshall interface

图4 离散元数字模型Fig.4 Discrete element digital model
2 细观模型疲劳损伤参数设置
沥青混合料的疲劳损伤主要表现为沥青胶浆内部以及沥青胶浆和集料之间的力学性能损伤,因此,在利用离散单元法模拟沥青混合料疲劳损伤时,只需研究作为接触模型定义的平行黏结接触模型的疲劳损伤,并用离散单元法对其描述和控制。
式(2)体现了沥青胶浆材料平行黏结直径衰减速率与时间、应力水平的关系[11]为:
(2)

控制虚拟疲劳试验参数设置如表1及表2。

表1 平行黏结损伤参数β1、β2、α1和α2值

表2 AC-13离散元模型力学参数
3 间接拉伸疲劳实验模拟及分析
3.1 棱角性对疲劳性能影响
同批次同配比的粗集料无法起到对比效果,为了得到棱角性不同的粗集料,故需按照规范[11]对粗集料做磨耗试验,将获取的5组不同磨耗转数粗集料图像投放生成不同棱角性的数字虚拟试件,数字试件棱角性参数和图样分别见表3及图5。
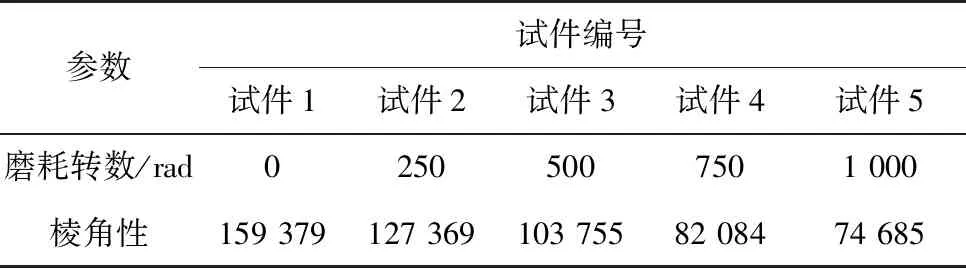
表3 数字试件棱角性
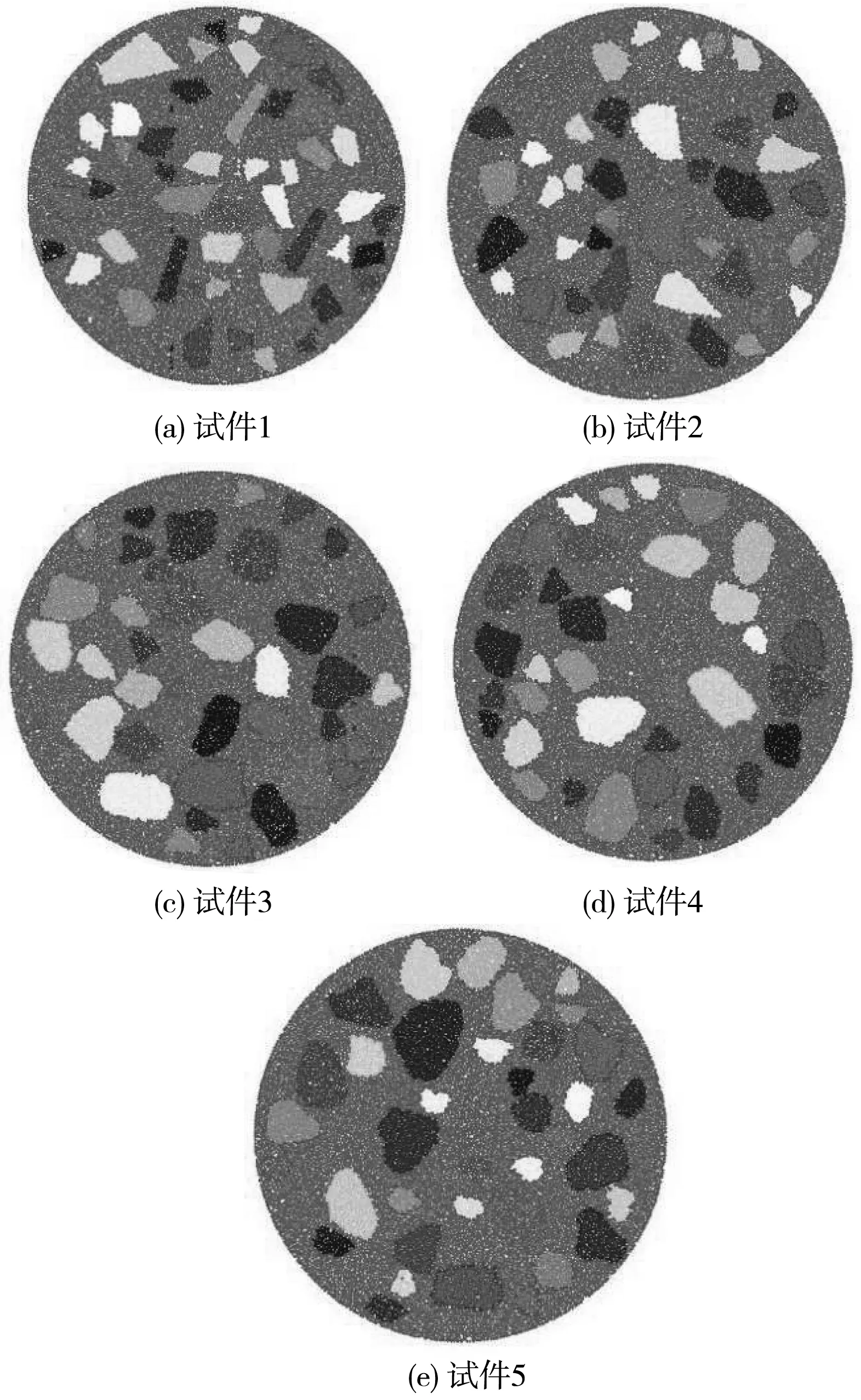
图5 不同棱角性参数虚拟试件Fig.5 Virtual specimens with different angularity parameters
通过编写离散元软件PFC2D内部fish代码可实现间接拉伸疲劳虚拟实验,实验结果如表4。

表4 试件虚拟疲劳实验结果
根据实验结果中疲劳寿命数据进行拟合即可得到不同棱角性特征下的应力疲劳方程,见表5,应力疲劳方程形式采用如式(3):
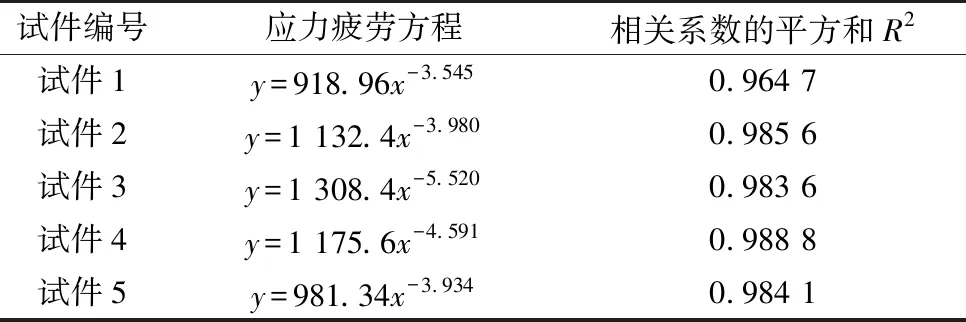
表5 不同棱角性特征下应力疲劳方程
N=kσ-n
(3)
式中:N为疲劳寿命;k和n则为特征参数。
由表5可看出,随着棱角性的增大k值先增大后减小,而k值的增长或减少同步表现为应力疲劳曲线截距的增大和减小,即意味着在棱角性增加的过程中抗疲劳性能出现了峰值。而n值的变化也与k值的变化较为同步,n值越小则表示混合料对应力的变化敏感性越小。
由以上数据可知,无论是在同等应力还是在同等应变情况下,其疲劳寿命在棱角性变化的梯度中都较为明显的存在一个峰值,该规律与表示应力疲劳曲线截距的k有较为直接的关系,故拟合棱角性与k值的函数优化应力疲劳方程,棱角性与k值拟合曲线图如图6。而对于n值的变化,由于应力区间较为集中,且变化幅度不明显,故不予研究。应力疲劳方程可根据式(3)优化改写为式(4):

图6 棱角性参数与k的拟合关系Fig.6 The fitting relationship between angularity parameter and k
N=(-240.312L2×10-6+345 320L-670.26)σ-n
(4)
式中:L为棱角性参数。
分析原因可得,当棱角性较低时,混合料内部的粗集料没能形成骨架结构,当应力增长到一定程度,内部应力便基本由沥青胶浆承担了,因此所表现的细观现象即加载中会较多出现分支裂缝,如图7。随着骨架形成,疲劳性能有所改善。但随着棱角性继续增加,粗集料的棱角性变得明显。而此时粗集料棱角处便会出现明显的应力集中现象,导致粗集料刺破沥青膜,形成裂缝,从而使疲劳性能再次降低,应力集中现象如图8。

图7 分支裂缝的产生Fig.7 Branch cracks generation
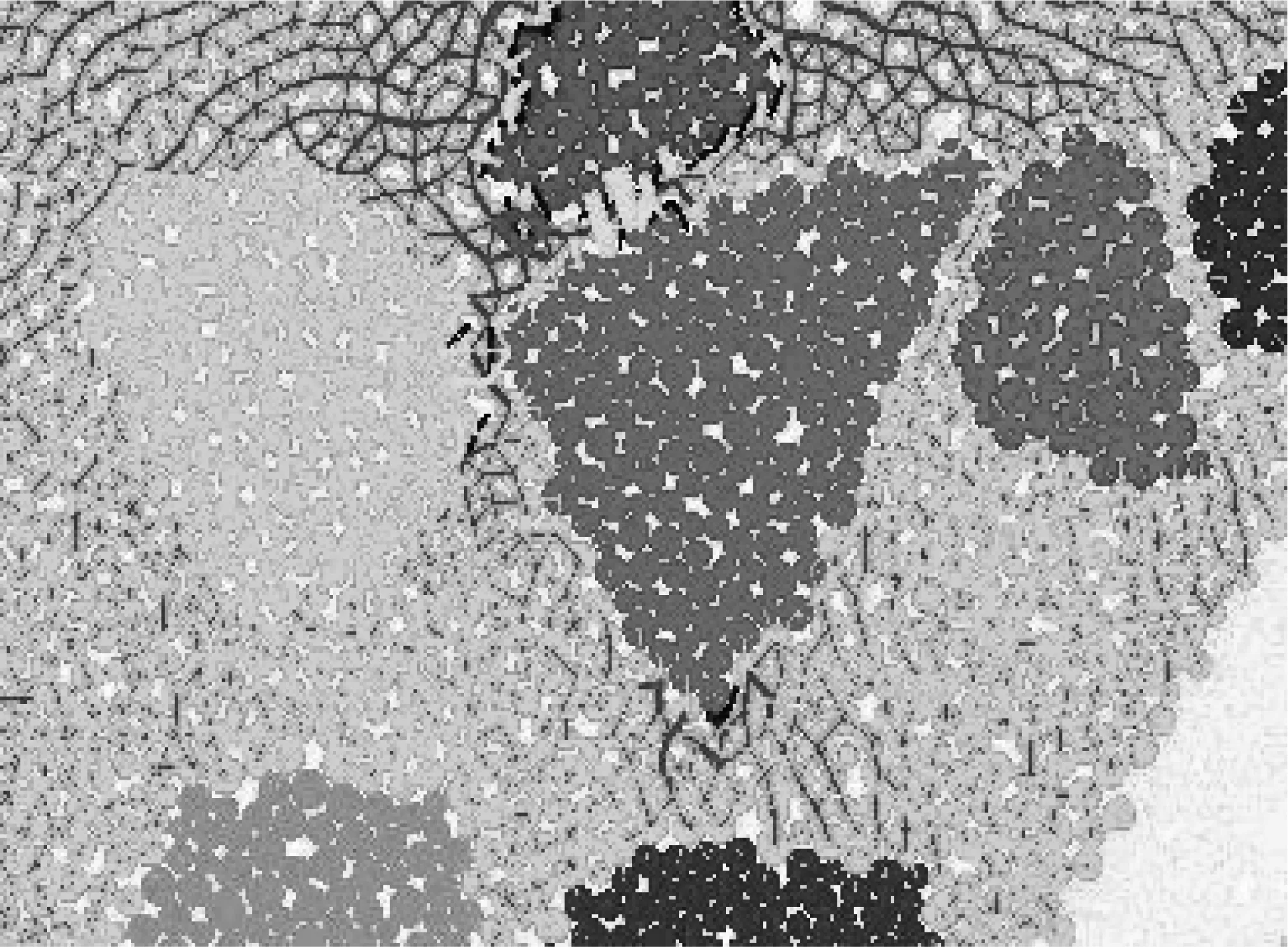
图8 应力集中现象Fig.8 Stress concentration phenomenon
3.2 接触细观特征对疲劳性能影响
重构5组不同接触细观特征的沥青混合料数字试件完成间接拉伸疲劳试验,其细观特征参数和试验结果分别如表6和表7。

表6 虚拟试件细观特征参数
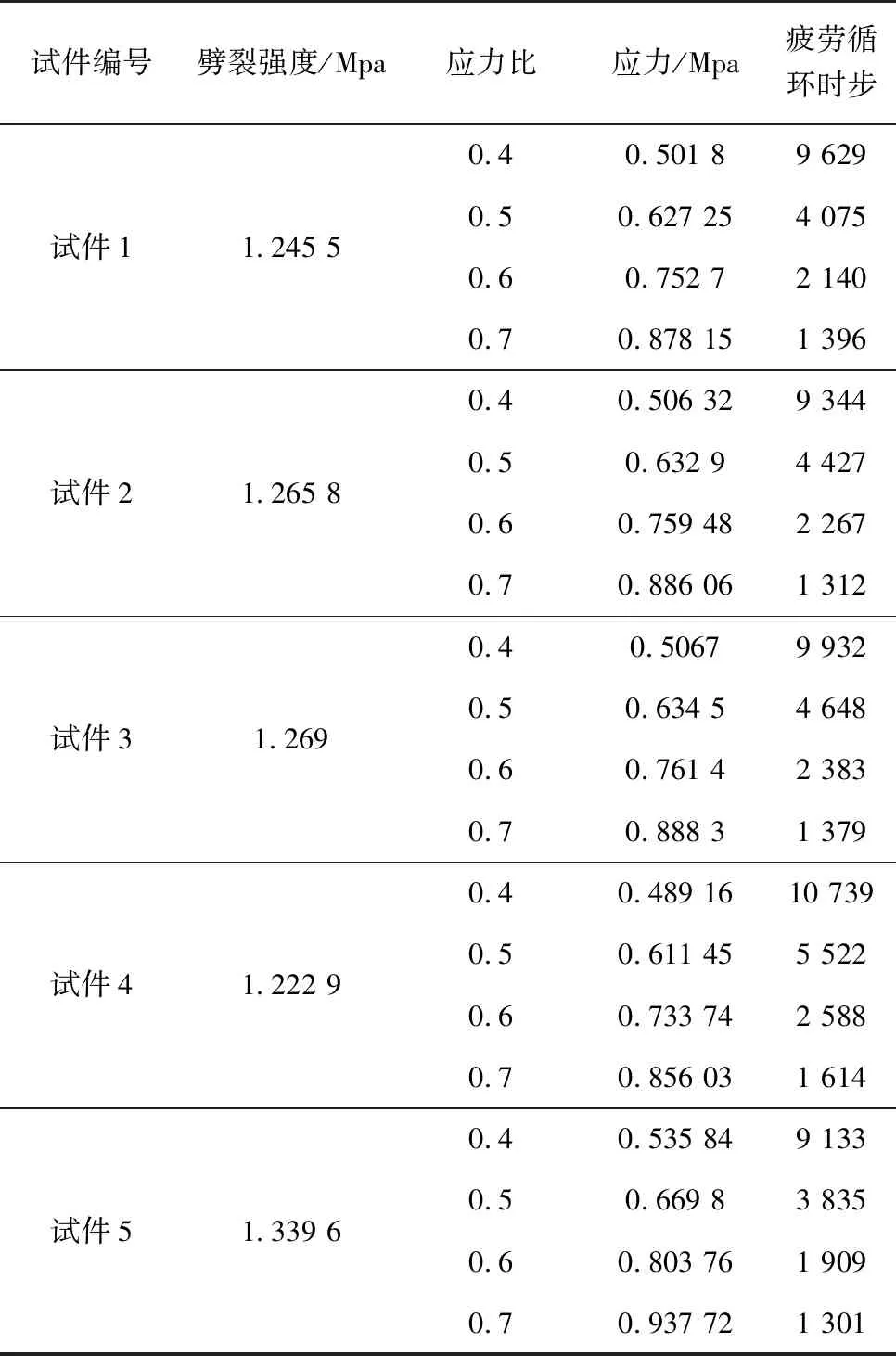
表7 虚拟间接拉伸疲劳试验结果
将虚拟疲劳实验数据代入式(3),可得各试件的应力疲劳方程,如表8。

表8 不同接触状态特征下应力疲劳方程
由表8可以看出随着接触对增大,k值呈现缓慢增大趋势,说明沥青混合料内部粗集料接触对的增多改善了沥青混合料抗疲劳性能。反观n值的变化趋势不明显,只在接触对数量达到级配内峰值时出现了一个变小趋势,即意味着接触对达到一个较高水平时,出现了对疲劳破坏敏感性的降低。
现对粗集料接触状态的细观特征参数引入应力疲劳方程中对其进行优化,针对以上应力疲劳方程中k值和n值与接触对参数的规律,将k值与接触对参数进行拟合,实现对应力疲劳方程的优化。拟合关系图如图9。

图9 接触对个数与k值的拟合关系Fig.9 Fitting relationship between the number of contact pairs and the value of k
运用以上k值与接触对参数的拟合可将式(3)优化改写为式(5):
N=(12.459J+663.07)σ-n
(5)
式中:J为接触对参数。
分析接触对数量变化对疲劳寿命产生影响的原因,随着接触对数量增加,可认为在同一数量级配的沥青混合料试件成型过程中,混合料内部形成了受力状态更为稳定的粗集料骨架,从而改善了沥青混合料抗疲劳性能。在同一数量级配前提下,当接触对数量达到了一个较高水平,n值出现一个较小范围下降,受力状态更好的粗集料骨架形成后,使沥青混合料对疲劳破坏的敏感性降低。
3.3 棱角性指标和接触对指标间的关系
根据生成的多组沥青混合料虚拟试件特征参数,绘制出棱角性参数和接触对参数的相关性图例,如图10。
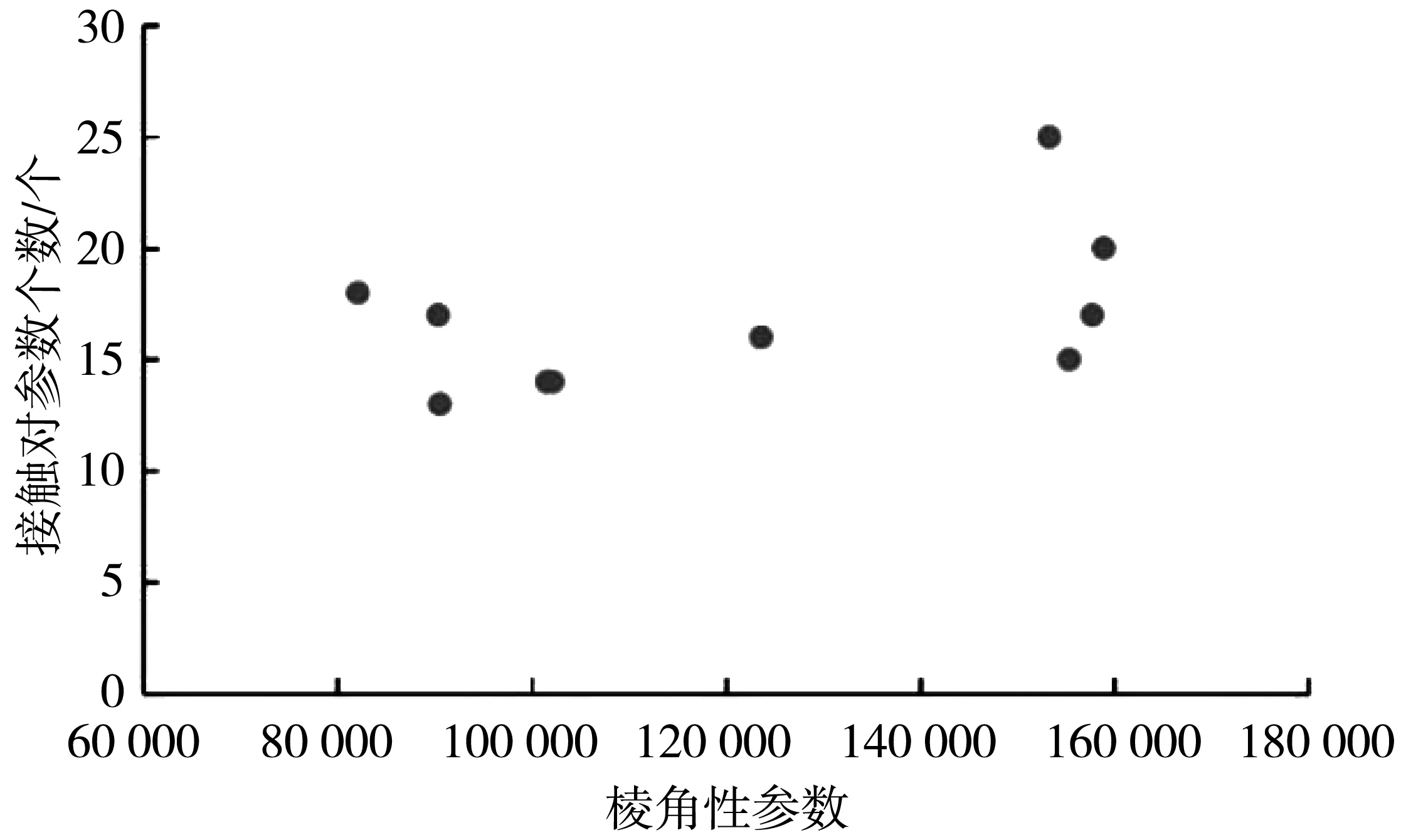
图10 棱角性与接触对相关性图例Fig.10 Correlation legend of angularity and contact pair
由图10可知,接触点参数与棱角性参数并无明显的相关性,故为了便于将2个参数引入同一疲劳方程,笔者假设棱角性和接触对2个细观特征不相关。由式(4)可知,k值与棱角性参数呈二次关系;
由式(5)可知,k值和接触对参数呈一次关系,故拟二次函数f(x,y)=ax2+bx+cy+d来表征k值,其中x为棱角性参数,y为接触点参数。将实验数据导入MATLAB中,利用MATLAB内置拟合工具CurveFitting实现拟合。然后将拟合函数代入应力疲劳方程中,得到式(6):
N=(-1.565×10-7L2+0.035 04L+15.59J-
1 032)σ-n
(6)
4 结 论
以粗集料的分布形态与沥青混合料疲劳性能关系为主要研究目标,从粗集料棱角性和混合料内部接触对状态2个细观特征入手,借助数字图像处理技术和离散元软件等,进行了粗集料分布形态对沥青混合料疲劳性能影响的研究,得到如下结论:
1)对于AC-13沥青混合料,当其棱角性参数在110 000~130 000之间时,抗疲劳性会出现峰值。在级配正常的接触对范围内,沥青混合料抗疲劳性能会随接触对的增加而增加。
2)将棱角性参数和接触对参数都分别引入应力疲劳方程,实现了对应力疲劳方程的优化。而后提取试件棱角性参数与接触对参数,研究2个参数的相关性,结果表明相关性不明显,并在假设两参数不相关的基础上,完成了对应力疲劳方程的双参数优化。
3)粗集料棱角性参数和接触对数量影响着沥青混合料的抗疲劳性能,对沥青混合料进行配合比设计时应给予关注。
