上市企业全要素生产率对其自生能力的影响机制——基于汽车制造业会计核算等式的研究

姚治国,朱聪浩,杨金朋

(1.丽水学院 商学院,浙江 丽水 323000;2. 天津外国语大学 国际商学院,天津 300270)

一、 引言与文献综述

党的二十大报告指出:“高质量发展是全面建设社会主义现代化国家的首要任务。”企业作为市场经济的主体,在经济发展中起着十分重要的作用,企业的高质量发展自然成为目前迫切需要研究的课题。在新古典经济学理论中,与企业高质量发展相关的概念是全要素生产率。目前相关文献大部分是研究企业全要素生产率受哪些因素的影响,很少研究企业全要素生产率对企业竞争力和生存能力的影响机制,往往侧重于研究企业全要素生产率对企业绩效的影响[1-3]。从企业自身的角度来看,高质量发展的目的是提高企业的竞争力和生存能力。因此,有必要研究企业全要素生产率对企业生存能力的影响机制。

“自生能力”的概念是Lin and Tan[4]于1999年首次提出的:如果一个企业通过正常的经营管理,预期能够在自由、开放和竞争的市场中赚取社会可接受的正常利润,那么这个企业就是有自生能力的,否则,这个企业就是没有自生能力的。从这个定义可以推断出,具有自生能力的企业往往具有生存能力。因此,本文认为,可以用新结构经济学中的自生能力来代表企业的生存能力。那么,应该从哪种角度去研究企业全要素生产率对其自生能力的影响呢?

在新结构经济学理论的视角中,企业的自生能力问题是企业在有限预算的情况下,面对不同资本和劳动力组合,需要选择相对成本较低的一个组合。因此企业自生能力与比较优势密切相关,两者都是由要素禀赋结构决定的[5]。由此产生了一系列从要素禀赋比较优势和技术比较优势的角度来实证研究企业自生能力的文献[6-10]。这种研究角度是基于新结构经济学理论,很难直接应用于来自新古典经济学理论的全要素生产率。有学者认为,比较优势不是影响企业自生能力的唯一因素,如果缺少技术优势和竞争优势,企业就很难有自生能力[11]。还有学者指出,竞争优势的一部分来源于交易成本[12],而竞争优势是由交易成本在内的总成本决定的,因此企业只有降低交易成本,才能将潜在的比较优势转变为竞争优势[13]。这给本文的研究带来了启发,根据企业自生能力的定义,企业净利润率(净利润/营业总收入)是自生能力的表现,企业实际发生的成本和费用在企业年报中均有详细记录。因此,本文试图通过企业年报利润表中的核算等式,来构建一座研究全要素生产率与自生能力之间作用关系的桥梁。

汽车制造业作为国家制造业的重要组成部分,经常受到国家政策的支持。2017年发布的《汽车产业中长期发展规划》(1)http://www.gov.cn/gongbao/content/2017/content_5230289.htm。明确指出,我国汽车产业“大而不强”的问题依然突出,表现在关键核心技术掌握不足,企业实力亟待提升。为推动新能源汽车产业的高质量发展,加快建设汽车强国,2020年10月20日,国务院发布了《新能源汽车产业发展规划(2021—2035年)》(2)http://www.gov.cn/zhengce/content/2020-11/02/content_5556716.htm。,明确强调我国新能源汽车发展面临着核心技术创新能力不强、市场竞争日益加剧等问题。上述两个政策表明,汽车制造业企业始终存在质量不高以及企业竞争力不强的问题。因此,研究汽车制造业企业全要生产率对其自生能力的作用机制具有较强的现实意义和针对性。

本文的贡献在于:(1)在理论上,一方面,通过柯布-道格拉斯(C-D)生产函数,论证新古典经济理论中企业全要素生产率和新结构经济学理论中企业自生能力的关系,提出企业全要素生产率能够提高其自生能力;另一方面,采用会计核算等式,拆分企业总成本,研究企业全要素生产率对其自生能力的作用机制,提出企业全要素生产率通过降低生产成本、交易成本、研发成本、财务成本来提高其自生能力,同时企业全要素生产率的提高能够缓企业解融资约束,进而提高企业自生能力。(2)在实证上,采用会计核算等式建立的模型具有一定的完备性,能够减少内生性问题对研究结论的影响。

本文的结构安排为:第二部分对上市企业会计核算等式进行理论分析,提出研究假说;第三部分介绍实证设计,包括计量模型设定、数据来源以及指标构建;第四部分通过实证结果,分析汽车制造业上市企业全要素生产率对其自生能力的影响;最后给出结论和建议。

二、 数学模型与理论分析

全要素生产率是新古典经济学理论中的一个概念。新结构经济学认为,新古典经济学中生产函数不变的假设不符合现实客观世界,生产函数应当是变化的[14]。但是目前很难对可变生产函数进行测算。因此,本文选择研究不变生产函数下的全要素生产率对企业生存能力的影响。

在企业层面测量全要素生产率主要有两种方式:一种是超越对数生产函数;另一种是柯布-道格拉斯(C-D)生产函数。本文主要考虑C-D生产函数下的全要素生产率与新结构经济学理论中生产函数的关系[14-15]。

C-D生产函数的数学形式为:

(1)

新结构经济学中生产函数形式为:

Y(t)=A(t)K(t)α(t)L(t)1-α(t)

(2)

在(1)式中,假定α、β不变,Y、K、L的任何变化都会导致A的变化。在(2)式中,Y、K、L的任何变化都会导致A(t)和α(t)的变化,而α(t)的变化在新结构经济学理论中被认为是生产结构发生了变化,这说明A(t)的变化可以看成是除了生产结构变化以外的变化。而A(t)的变化包含很多因素,如果认为这些因素是在K和L不发生变化的情况下,A(t)发生变化而导致Y的变化,那么全要素生产率的变化可以用来表示A(t)与α(t)的变化。比如,一家企业的生产工人一开始一小时只能生产6个单位产品,在机器和工人数量没有发生变化的情况下,通过参加学习和培训,一小时可以生产8个单位产品,这个产出的变化就是完全由A(t)带来的。最后,需要明确的是A(t)和α(t)的变化方向,一般情况下,对于一个正常经营的公司,其生产结构是不断升级的,其管理方式和工人的学习能力是不断进步的;而对于一个经营不当的公司,其管理方式可能先出问题,随后导致公司的生产停滞不前,甚至出现变卖资产的情况。因此,本文认为A(t)和α(t)是同向变化,全要素生产率与A(t)、α(t)均为同向变化。基于此,提出假说1。

假说1:企业全要素生产率的提高有利于增强企业的自生能力。

全要素生产率的提高通常有两种途径:一是通过技术创新;二是通过效率变革[16-17]。全要素生产率的提高带来产量的提高。新古典经济学理论认为,企业单位成本的产出提高,意味着企业单位产出的成本下降。从汽车制造行业公司的实际生产和整个销售环节来看,产量的提升意味着单位产出的生产成本、销售费用、管理费用、研发费用、财务费用的下降。如果假设产出产品的平均价格不变,并且认为影响产出的变量除全要素生产率之外均为外生,企业营业利润通过(3)式来表示:

Π=R(Q(A))-C-C(Q(A))-C1-C1(Q(A))-Z1

(3)

其中,Π为利润总额,A为全要素生产率,Q(A)为产量关于全要素生产率的函数,R(Q(A))为企业收益关于产量Q(A)的函数,C为不受Q影响的生产成本,C(Q(A))为企业可变生产成本关于产量Q(A)的函数,C1为各种不受Q影响的固定交易成本,C1(Q(A))为受Q影响的各种期间费用(销售费用、管理费用、研发费用、财务费用),Z1为税金及附加与损益的总和。

进一步地,企业净利润通过(4)式来表示:

Π1=R(Q(A))-C-C(Q(A))-C1-C1(Q(A))-Z1-Z2

(4)

其中,Z2包括营业外收入、营业外支出、企业所得税。

再对(4)式左右两边同时除以R,得:

(5)

假设企业存在一个不变产品价格,得:

R=P×Q(A)

(6)

再把(6)式代入到(5)式,得:

(7)

从(7)式可知,全要素生产率可以通过单位产出的生产成本和期间费用来影响企业净利润率。单位产出的生产成本取决于单位产出的不变生产成本和可变生产成本。如果进一步假设生产成本和期间费用与产量是稳定的一阶线性关系,即单位产出需要的生产成本和期间费用不变,那么随着产出的增加,单位产出的生产成本和期间费用下降,进而使企业的净利润率上升,也就是企业自生能力的提高。

本文利用交易成本这个概念对期间费用进行进一步分类。目前对于交易成本并无统一的定义[18-19]。上市企业中有四大期间费用,一般把管理费用认为是交易成本的一部分[20-21],但对于另外三大费用并无多少讨论。如果将交易成本分为内生交易成本和外生交易成本,其中,内生交易成本是市场均衡与帕累托最优之间的差别,外生交易成本是指在交易过程中直接或间接发生的费用[22]。本文认为销售费用也是交易成本,而研发费用与财务费用不能认为是交易成本。基于此,提出假说2。

假说2:企业全要素生产率主要通过降低单位产出的生产成本和交易成本以及研发费用与财务费用来提高企业自生能力。

现有研究并未涉及融资约束对企业自生能力的影响,尚未关注融资约束在企业全要生产率对企业自生能力的影响中到底扮演何种角色。企业绩效与企业自生能力的含义较为接近,因此,本文借鉴有关融资约束对企业绩效影响的研究文献。刘耀栋[23]发现,大部分学者认为融资约束抑制了企业获得资金的能力,从而不利于企业的发展。因此本文认为,一方面,融资约束过高会使企业资金紧张,无法更好地投入生产,进而降低企业自生能力;另一方面,全要素生产率的提高能够增加企业收入,缓解融资约束,进而提高企业自生能力。基于此,提出假说3。

假说3:企业全要素生产率的提高可以缓解融资约束,从而提高企业自生能力。

三、 实证设计

(一) 模型构建

为评估企业全要素生产率对其自生能力的影响,设立如下模型:

ZSNLit=α0+α1TFPit+∑Controlit+δi+λt+εit

(8)

其中,i表示企业,t表示年份,ZSNLit表示i企业t年的自生能力,TFPit为i企业t年的全要素生产率。Control为控制变量集合,具体包括企业年龄、企业规模、税金成本、损益成本、营业外收入、营业外支出、实际税率。δi为企业固定效应,λi为时间固定效应,εit为随机误差项。对于绝对值变量采取对数化处理。

本文选择Driscoll-Kraay标准误进行估计,同时把其他标准误作为检验稳健性的一种方法进行报告。为了检验机制假说,构建如下计量模型:

QYCBit=α0+α1TFPit+∑Controlit+δi+λt+εit

(9)

ZSNLit=α0+α1TFPit+RZYSit+TFPit×RZYSit+∑Controlit+δi+λt+εit

(10)

其中,QYCBit为企业成本机制变量,包括生产成本、交易成本、研发成本、财务成本;RZSY为企业融资约束,表示全要素生产率的调节变量。

(二) 变量及数据说明

1. 样本选取

本文选取2008—2021年中国汽车制造业上市公司的财务数据。参照中证指数2021版对汽车行业的划分,该版本的优点是准确度高,并且对于公司所处行业的一级、二级、三级、四级都有详细划分。本文后续对汽车产业链的划分也是参考其三级行业的划分方式。由于中证指数2021版中缺少汽车芯片相关公司的数据,为完善样本,参考东方财富中的汽车芯片概念,加上其中的公司,总共为240家汽车制造业上市公司。

2. 企业自生能力指标的选取

根据林毅夫对自生能力的定义[5],借鉴现有文献[6,10,24-25],本文的企业自生能力用利润率来衡量(企业的净利润除以总收入)公式如下:

(11)

3. 机制变量的选取

(1)生产成本(SCCB),用企业营业成本与企业总收入的比值来表示。(2)交易成本(JYCB),用企业管理费用与销售费用之和与企业营业总收入的比值来表示。(3)研发成本(YFCB),用研发费用与企业营业总收入的比值来表示。(4)财务成本(CWCB),用财务费用与企业营业总收入的比值来表示。(5)融资约束(RZYS),主要有四种测算指数:KZ指数、WW指数、SA指数、FC指数。由于张金鑫和王逸[26]提出FC指数的测算方法能够很好地反映中国上市公司的融资约束问题,因此本文选取FC指数作为融资约束的测算指标。

4. 核心解释变量的选取

目前关于全要素生产率(TFP)的测算方法主要有OP法、LP法和ACF法,但是这三种方法都有其缺陷。Olley and Pakes[27]最早提出用公司投资水平进行两步一致估计法,解决同时性偏差。Levinsohn and Petrin[28]对OP法进行改进,提出了LP法,将中间投入作为生产率的代理变量。Ackerbergetal.[29]认为OP法和LP法的第一步估计系数可能存在严重的共线性问题,提出用ACF方法计算。而Wooldridge[30]基于GMM的一步估计法,提出Wooldridge估计,克服了ACF估计在第一步估计中潜在的识别问题,并且能够得到稳健标准误。但是由于加入滞后项会损失观测值,鲁晓东和连玉君[15]提出用MrEst估计法(动态面板工具变量方法)进行修正。

目前,在企业全要素生产率计算中,较少考虑到公司的产出应为产出增加值[31-33],因此,有必要准确计算上市公司的产出增加值。根据会计核算、会计报表以及现有工业企业数据研究对产出增加值的核算[9],本文认为,产出增加值=营业总收入-营业总成本(营业成本+税金及附加+费用)+税金及附加+应付职工薪酬-期初存货+期末存货。本文在基准回归中用企业总收入和企业产出增加值计算的MrEst法进行对比,在稳健性检验中用LP法、OP法、ACF法、WRDG法替代被解释变量。

5. 控制变量的选取

为尽可能控制影响企业自生能力的因素,本文选取的控制变量如下:(1)税金成本(SJCB),用税金及附加除以营业总收入来计算;(2)损益成本(SYCB),先计算营业利润、营业成本以及四大费用之和与营业总收入的比值,再用1减去其比值后得到;(3)营业外收入(YYWSR),用营业外收入除以营业总收入来计算;(4)营业外支出(YYWZC),用营业外支出除以营业总收入来计算;(5)实际税率(SJSL),用企业所得税总额除以营业总收入来计算;(6)企业年龄(QYNL),用当年年份减去企业成立年份来计算;(7)企业规模(QYGM),用企业总资产的对数化值来表示。主要变量的描述性统计结果如表1所示。

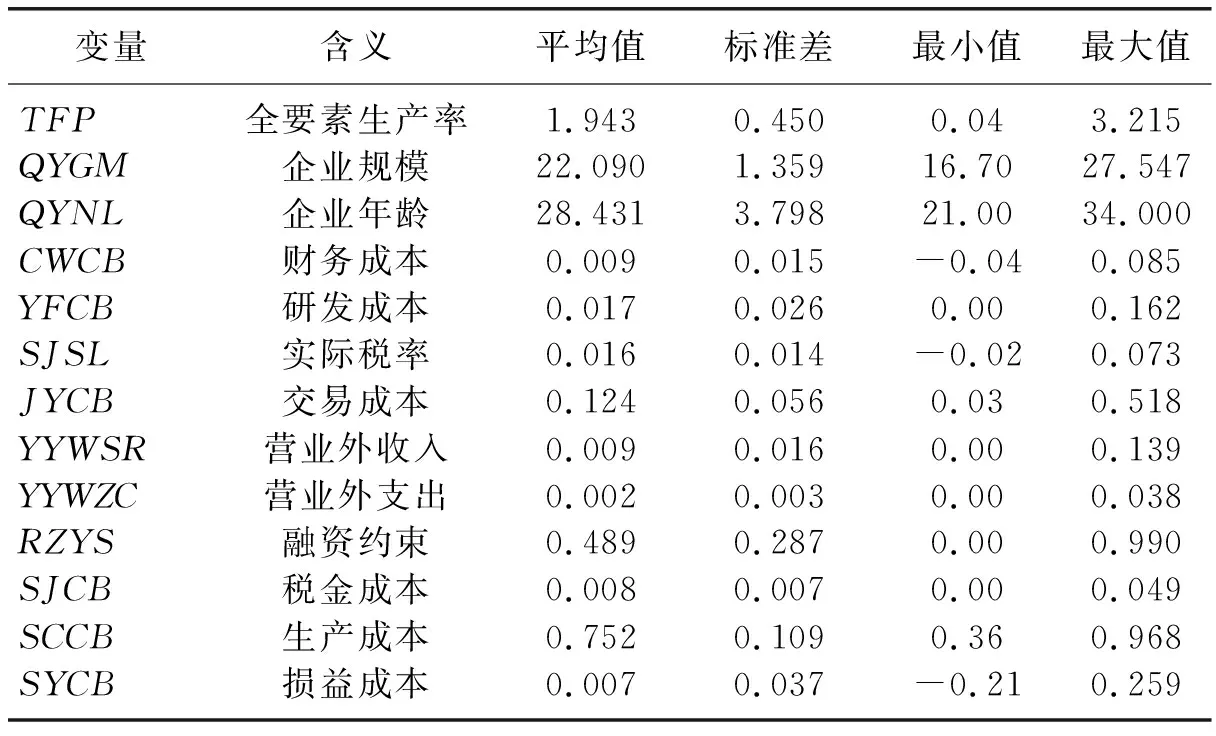
表1 主要变量的描述性统计结果

四、 实证结果及分析

(一) 基准回归结果及分析

表2是用全样本的回归结果。其中,列(1)是采用企业总收入中的增加值计算出的全要素生产率对企业自生能力的回归结果,列(2)是利用企业总收入计算出的全要素生产率对企业自生能力的回归结果。R2由0.593提高到了0.783,说明本文采用企业产出增加值计算出来的全要素生产率能够更好地反映企业自生能力的变动情况;系数从0.0363提高到了0.0801,说明用公司总收入计算的全要素生产率显著低估了其对公司自生能力的影响。

表2 企业全要素生产率与自生能力:基准回归结果

(二) 稳健性检验

1. 替换被解释变量和不同的标准误

本文选取企业净利润率作为衡量企业自生能力的指标,这个指标并未考虑行业层面带来的影响。

因此将企业净利润率除以行业平均净利润率作为新的衡量企业自生能力的指标,来减弱行业整体净利润率下降对企业自生能力的影响。现有关于企业自生能力的研究还较多关注资产回报率(ROA)。本文认为两者的区别主要在于研究对象资金周转频率是否较高。一般来说,周转率较高的企业往往净利润率较低,但不代表其自生能力低。因此,本文还选择企业ROA除以行业ROA替代被解释变量进行稳健性检验。

表3中的列(1)为考虑行业利润率的回归结果,发现企业全要素生产率的系数显著为正,说明在考虑行业利润率的情况下,回归结果基本稳健。列(2)表示资金周转率不同时的回归结果,发现企业全要素生产率的系数显著为正,说明在考虑资金周转率情况下,回归结果基本稳健。列(3)是聚类稳健标准的回归结果,发现企业全要素生产率的系数显著为正,说明在不同标准误下,回归结果基本稳健。

表3 企业全要素生产率与自生能力(稳健性检验1)

2. 替换核心解释变量

企业全要素生产率的测算方法有很多种,其中动态面板工具变量法从理论上来讲更优,但是为了避免单一测算方法带来的偶然性和内生性问题,需要通过OP法、LP法、ACF法、WRDG法计算的企业全要素生产率来进行稳健性分析。

表4中的列(1)是用LP法计算企业全要素生产率的回归结果,列(2)是用ACF法计算企业全要素生产率的回归结果,列(3)是用OP法计算企业全要素生产率的回归结果,列(4)是用ACF法计算企业全要素生产率的回归结果,列(5)是用WRDG法计算企业全要素生产率的回归结果。通过比较发现,企业全要素生产率系数的符号和显著性均不变,因此本文认为选择的企业全要素生产率计算方法较为稳健。

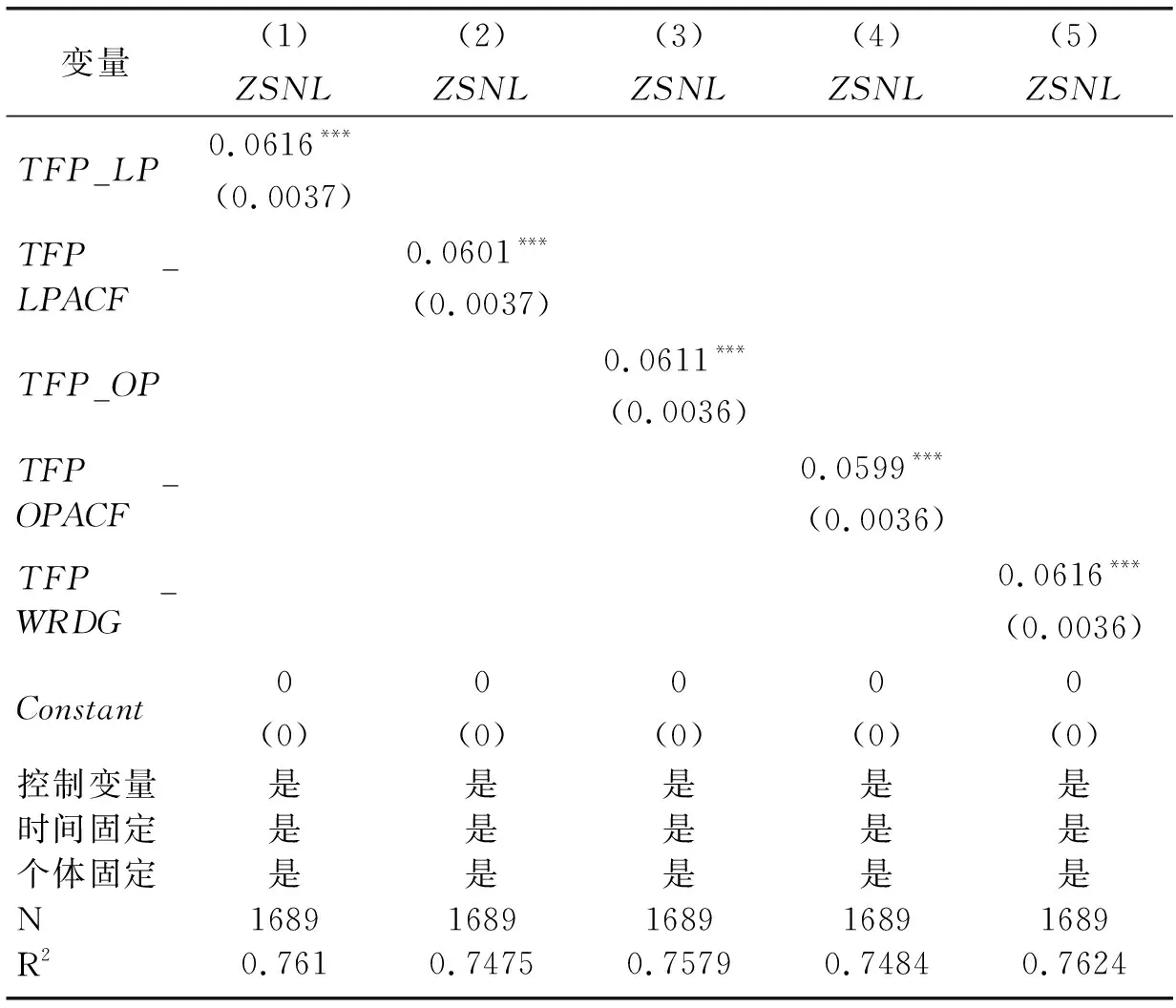
表4 企业全要素生产率与自生能力(稳健性检验2)

3. 内生性处理

双固定效应模型往往存在一定的内生性问题,因此有必要对模型进行梳理。内生性问题主要有三大来源:一是遗漏变量,从模型来看,本文研究企业全要素生产率通过降低生产成本和期间费用对其自生能力的影响,而其他变量对自生能力的影响均控制,因此本文认为存在遗漏变量的可能性较小;二是双向因果关系,从理论上讲,企业全要素生产率影响企业其能力,此外,存在企业自生能力影响其全要素生产率的可能性,因此本文选用自生能力的一阶滞后项作为工具变量,进行内生性检验[34];三是度量误差,包括解释变量度量误差和被解释变量度量误差,本文在稳健性检验中替换了解释变量和被解释变量,因此这部分不用再重复考虑。

考虑到企业自生能力可能具有连续性,即当期之后几期的自生能力也可能较弱。尝试选取自生能力的滞后一期和滞后两期来构建动态面板模型,并且采用系统广义矩估计模型(SYS-GMM)进行回归,同时本文选取的是非平衡面板数据,且存在异方差和当期截面自相关,采用BCFE估计进行修正。

表5中的列(1)报告了工具变量法的回归结果,列(2)至列(5)分别是混合模型、固定模型、SYS-GMM模型、BCFE模型的估计回归结果。列(1)通过了不可识别检验和弱工具变量检验,但是并未通过内生性检验,即P值为0.3108>0.1,因此认为双向因果方面的内生性问题较小。SYS-GMM模型中全要素生产率系数具有一致性的条件是,因变量滞后一期的估计系数要处于混合回归模型和双向固定效应模型的因变量滞后一期的估计系数之间。列(4)中自生能力滞后一期的估计系数在列(2)和列(3)中自生能力滞后一期的估计系数之间,且AR(1)的P值为0.000,AR(2)的P值为0.379,Sargan检验和Hansen检验均通过,说明自生能力的系数估计较为准确。列(5)为考虑异方差和当期截面自相关的BCFE估计,自生能力滞后一期系数在列(2)和列(3)估计的系数范围之间。因此,该模型自生能力的系数估计最为准确,说明基准回归模型低估了全要素生产率对自生能力的影响。

表5 企业全要素生产率与自生能力:内生性处理

4. 机制检验

上述研究表明,企业全要素生产率对其自生能力能够产生促进作用,本文接下来通过机制变量来检验企业全要素生产率对其自生能力的影响。

表6报告了五类机制变量的回归结果。其中,列(1)是以生产成本作为因变量的回归结果,企业全要素生产率的估计系数显著为负,说明全要素生产率的提高可以有效降低企业生产成本,符合本文的理论逻辑。列(2)是以交易成本作为因变量的回归结果,企业全要素生产率的估计系数显著为负,说明全要素生产率的提高可以有效降低企业交易成本,符合本文的理论逻辑。列(3)是以研发成本作为因变量的回归结果,企业全要素生产率的估计系数为负,显著性较弱,说明全要素生产率的提高可以有效降低企业交易成本,符合本文的理论逻辑。列(4)是以财务成本作为因变量的回归结果,企业全要素生产率的估计系数显著为负,说明全要素生产率的提高可以有效降低企业财务成本,符合本文的理论逻辑。上述四列回归结果表明假说2正确。对比这四列中企业全要素生产率的系数发现,企业全要素生产率主要是通过降低企业生产成本来提高企业自生能力,较少通过降低交易成本、财务成本和研发成本来提高企业自生能力。列(5)是用融资约束作为调节变量的回归结果,融资约束系数为负,企业全要素生产率与融资约束交叉项为正,表明假说3正确。

表6 企业全要素生产率与自生能力:机制检验1

5. 异质性分析

由于不同类别的企业全要素生产率对其自生能力的影响具有差异性,因此本文从企业性质、地区、产业链三个角度进行异质性分析。根据中证指数行业分类2021版的三级行业划分,将生产汽车零部件与轮胎的企业划分为上游企业,将生产乘用车和交通运输设备的企业划分为中游企业,将汽车经销商与提供汽车服务的企业划分为下游企业,而将生产汽车芯片的企业划分为芯片企业。

表7报告了按企业性质划分的回归结果。国有企业全要素生产率系数为0.0643,民营企业全要素生产率系数为0.109,外资企业全要素生产率系数为0.0816,说明相比于国有企业和外资企业,民营企业全要素生产率能够更加有效地作用于企业自生能力。根据现有文献[6],从比较优势的角度来看,民营企业比国有企业更具有自生能力,因此,本文认为,由于民营企业更加具有禀赋比较优势和技术比较优势,因此,企业全要素生产率提高能够更好地降低生产成本,进而提高企业自生能力。

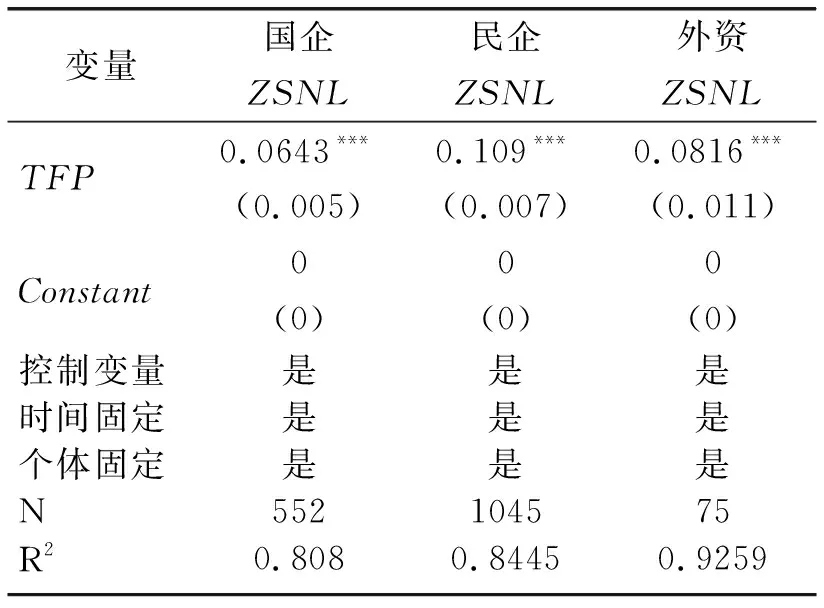
表7 企业全要素生产率与自生能力:异质性分析1

表8报告了按产业链划分的回归结果。相比于制造业下游和中游生产企业,汽车制造业上游和汽车芯片生产企业全要素生产率能够更有效地提升企业自生能力。其原因可能是上游和汽车芯片生产企业具有较高的生产复杂性。例如,芯片生产过程涉及高度精密的工艺(光刻、刻蚀、离子注入等),上游零部件的生产过程通常包括多个环节(铸造、锻造、机加工、热处理、表面处理等)。因此,相比于中游和下游的生产企业,上游和汽车芯片生产企业全要素生产率的提高,更能有效地降低生产成本,进而提高企业自生能力,同时我们发现,相比于中游和下游的生产企业,上游和汽车芯片生产企业更加依赖和需要全要素生产率的提高。

表8 企业全要素生产率与自生能力:异质性分析2

五、 结论与政策建议

本文基于会计核算等式,从理论和实证上分析了企业全要素生产率对其自生能力的作用机制。主要结论如下:(1)企业全要素生产率与企业自生能力存在显著的正相关关系。(2)通过机制检验发现,企业全要素生产率主要是通过降低企业生产成本,较少通过降低企业交易成本、研发成本、财务成本来提高企业自生能力,同时企业全要素生产率的提高能够缓解融资约束,进而提高企业自生能力。(3)通过异质性分析发现,国有企业全要素生产率对其自生能力的作用效果明显低于民营企业,中游和下游生产企业全要素生产率对其自生能力的作用效果显著低于上游和汽车芯片生产企业。

基于上述结论,本文提出如下建议:(1)对于整个汽车行业生产企业来讲,应积极提高全要素生产率,进而提高企业自生能力。具体而言,一方面,通过加大研发投入,提高企业创新能力;另一方面,构建全生命周期管理体系,提高资金的利用效率。(2)提高金融中介机构对企业的贷款支持力度,缓解企业融资成本,重点支持具有创新能力和发展潜力的汽车制造业企业。政府还应对贷款资金的管理和运作进行有效监督,确保资金的合理使用。(3)国有企业应当进行精细化管理,从而更好地把握市场机会,提高生产效率,降低运营成本,提升产品品质,从而增强企业的竞争力。另外,国有企业应该挖掘自身潜力,建立激励机制,让员工更加积极主动地投入到工作中。除此之外,国有企业也应该加强与外部的合作和创新,引进新技术、新工艺和新产品,提高产品质量和附加值,提升企业全要素生产率和自生能力。(4)对于汽车产业链上游生产企业,一方面,要加大研发投入,提高产品竞争力;另一方面,培育和弘扬精益求精的工匠精神,树立质量为先、信誉至上的经营理念,推进“品质革命”,推动“中国制造”走向“精品制造”。(5)对于生产汽车芯片的企业,大力推进以项目为主导的联合开发,促进形成国际化战略联盟或者校企联盟,降低研发成本,加速提升自主研发能力,提高企业全要生产率,增强企业自生能力。