圆锥曲线中斜率定值问题的再探究

浙江省丽水中学 (323000) 赵凯菲

圆锥曲线中的定点定值问题是历年高考考查的热点问题．对于斜率之和、斜率之积为定值的圆锥曲线模型,利用韦达定理的常规解法运算量较大,比较好的办法是齐次化构造[1]．本文从另一角度,以两个引理为切入点解决此类问题,给我们带来很大的方便．

一、两个引理

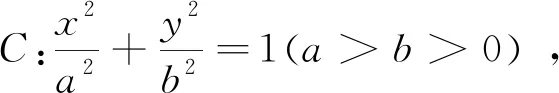
仿引理1证明易得:

利用这两个引理可以证明以下几个结论．

-b2(x1-x0)(x2+x0)+a2(y1-y0)(y2+y0)=a2λ(y2+y0)(x1-x0),以上两式相减得-2b2x0(x2-x1)+2a2y0(y2-y1)=

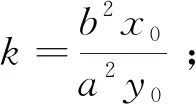
事实上,当λ=0时,kAP+kAQ=0,从几何角度可以发现直线PQ的斜率与椭圆在点A处的切线斜率互为相反数．

类似地,可以将以上结论推广到一般的双曲线．