非对称柔性支撑龙门双驱平台的解耦与同步控制

位广宇, 谷朝臣, 杨舒盛, 关新平

(上海交通大学 自动化系; 系统控制与信息处理教育部重点实验室;上海工业智能管控工程技术研究中心,上海 200240)

龙门双驱运动平台是一种线性运动平台,平台两侧各安装一组永磁直线同步电动机(后文简称电机),共同推动横梁运行, 横梁上安装驱动装置带动负载设备运行.双驱平台能克服单驱系统两侧不同步的问题,同时拥有双电机所提供的更强推力,因此具备更高的定位精度和控制带宽,被广泛应用于晶圆切割、激光雕刻、慢走丝机床、高速点胶和表面贴装技术(SMT)等精密运动控制场合,涵盖半导体加工、机械制造和3C电子等多种领域.

龙门双驱平台横梁与滑动底座的支撑方式分为刚性和柔性支撑.在传统的刚性支撑龙门双驱系统中,横梁一旦因外力和控制不当等因素出现偏转,势必引入横梁和导轨间的内力,进而恶化系统控制性能,甚至出现破坏导轨等极端情况[1].采用柔性支撑结构,能在一定程度上消除龙门双驱机械系统的“过耦合”,极大程度降低横梁与导轨间的内力,避免系统控制特性崩塌[2].

双驱动轴的同步性能是影响龙门双驱系统定位精度的关键因素.由于失去了刚性导轨的硬约束,柔性支撑龙门双驱平台的同步性能更易受到机械耦合和内外扰动的影响.因此,建立柔性支撑龙门平台的动力学模型,并在此基础上设计控制器架构与控制算法以解决柔性龙门双驱系统的解耦与同步控制问题是学术界的研究热点.早期研究采用主-主、主-从等运动协调方法设计控制器[3],这类方法忽视了龙门双驱耦合机理,不能满足高动态精密控制的需求,需进一步分析龙门系统模型后,找出系统的耦合本质和影响双驱同步性能的关键因素;文献[4]采用拉格朗日方程建立了柔性龙门双驱系统的集总参数动力学模型,指出龙门两侧机电特性差异、负载的位置与加速度是影响两轴不同步的关键因素;Ma等[5]针对柔性结构的刚度问题,提出了机电参数集成设计与优化方法,并指出柔性支撑结构使得系统存在隐藏的高阶模态;Kamaldin等[2]为了提高龙门跟踪性能,同时避免高频控制信号激发高阶模态,采用RISE控制器以获得柔顺的加加速度.但这些研究对柔性支撑结构的等效方法仅考虑了其回转而忽略了横梁偏转所需的横向变形,因此需要结合实际对模型进一步改进.近年来,一些研究将龙门机械耦合作为扰动,采用扰动观测器进行解耦以提升同步性能[6-8].扩张状态观测器(ESO)[9]是一种将串联积分模型作为系统标称模型并将标称模型以外的动态扩张为新状态(总扰动)的观测器,其最大特点在于对被控模型所需信息少[10],能极大降低模型不确定性和外部扰动对控制器参数的影响,并在多类控制问题中应用[11].然而对于龙门双驱这类强耦合非线性系统,因耦合的存在使得系统偏离积分串联型模式,经典ESO将取得有限的效果,且无法及时跟踪并抑制耦合带来的扰动.目前采用ESO对龙门双驱系统控制的研究较少,文献[12]给出了基于ESO的龙门双驱控制方法,但对被控模型的过度简化使之丢失了大部分耦合动态,在设计ESO时也未对关键耦合因素进行补偿.因此,将影响龙门双驱同步性能的关键因素考虑到ESO的设计中,研究一种基于模型补偿ESO的龙门双驱解耦与同步控制框架,对于龙门双驱控制问题具有重要意义.

基于本文研究者所提出的一种回转和偏扭变形组合的非对称柔性龙门支撑结构[13],构建基于拉格朗日方程的高精度龙门双驱平台动力学模型.基于模型分析,将龙门双轴同步控制分解为平动和转动控制回路,针对影响系统动态和导致回路间耦合的关键因素,设计带有耦合项模型补偿的速度环二阶线性扩张状态观测器(LESO)和转动环三阶LESO,实现回路间的动态解耦并抑制负载动态对转动通道的影响,显著提升了双驱系统动态响应和抗扰性能.该控制架构与算法全部在自主开发的龙门双驱伺服驱动器中实现,应用于自主搭建的1.2 m 跨度龙门试验台,具有0.4 μm光栅尺分辨率下0.613 μm的重复定位精度.

1 非对称柔性支撑龙门双驱平台动力学模型

1.1 系统描述

非对称柔性支撑龙门双驱实物平台及非对称柔性支撑结构如图1所示,其中非对称柔性支撑由回转和偏扭两种结构组成,R为微动体回转形变,Δ为微动体横向拉伸形变.平台的模型示意图如图2所示,其中C1、C2表示两侧底座及各自连接的柔性支撑,B表示横梁,H表示负载工作头,均以点的形式表示;其他参数的定义和大小如表1所示.

表1 龙门双驱试验台参数Tab.1 Parameters of dual-drive gantry test bed

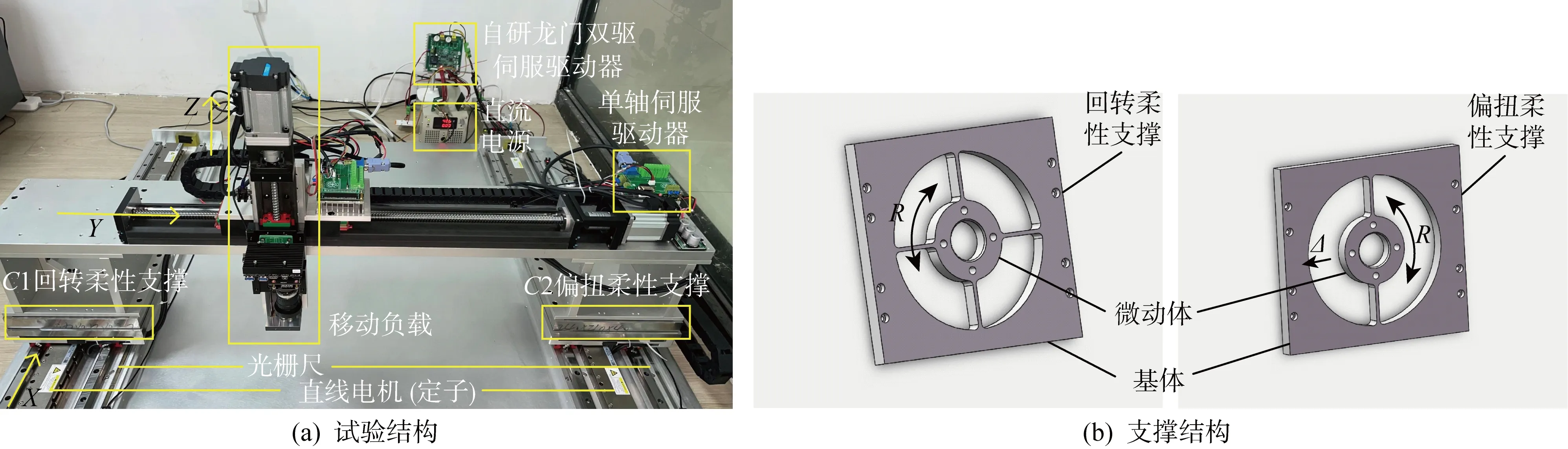
图1 非对称柔性支撑龙门双驱试验平台与其柔性支撑结构示意图Fig.1 Asymmetric flexure-linked dual-drive gantry test bed and its flexible supporting structures

图2 非对称柔性支撑龙门双驱运动平台模型示意图Fig.2 Modeling diagram of asymmetric flexure-linked dual-drive gantry positioning stage

定义笛卡尔坐标系xOy和广义坐标:

q3×1=[XgΘgYg]T

Xg=x1

Θg=arctan((x2-x1)/Lr)

1.2 动力学建模

在选定广义坐标后,双驱系统的动力学模型可由拉格朗日方程得到:

(1)

式中:Qj为广义力[14],有[Q1Q2Q3]T=[FC1+FC2LrFC2FY]T;L为拉格朗日量,由系统动能T、系统势能V组成;D为耗散函数,分别定义如下:

(2)

将式(2)代入式(1),得到系统动力学方程:

(3)

(4)

(5)

2 基于模型补偿ESO的控制回路设计

2.1 平动速度环控制模型与解耦控制器设计

在不改变伺服系统串级控制的前提下,考虑平动通道速度环控制的解耦设计.直线电机的推力由q轴电流控制,推力常数为Kf;又考虑到电流环带宽远高于速度环,可以认为速度环输出的电流给定与实际电流近似相等,因此将式(3)表示的龙门平动方程改写为以下形式

(6)

(7)

其中:

基于上式设计带有模型补偿的二阶线性扩张状态观测器:

(8)

(9)

(10)

式中:s为拉氏域中的复变量;RT(·)为干扰rT(t)的拉氏变换.

(11)

(12)

表明在上述控制律和模型补偿LESO作用下,平动速度环能实现与角度环的动态解耦和对阶跃给定速度的无静差控制.

2.2 转动角度环模型与解耦控制器设计

(13)

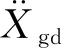
类似于平动速度环LESO设计,令ζ1=Θg,yR=ζ1并将总扰动项扩张为新状态ζ3=fR,设其导数为rR,则式(13)可以写作:

(14)

其中:

基于上式设计带有模型补偿的三阶LESO为

(15)

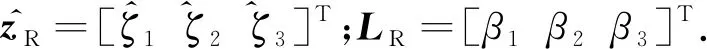
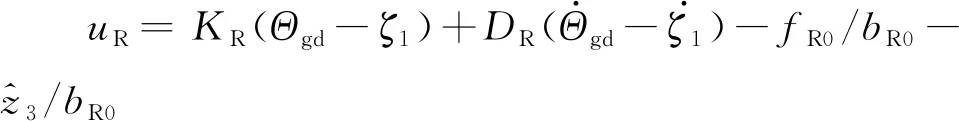
(16)

从而获得转动角度环的近似闭环传递函数:

(17)

其中:

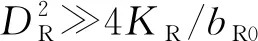
2.3 解耦与同步控制框架

通过设计平动速度环与转动速度环,能够实现两种控制目标的协调,即龙门在X轴方向的运动控制与龙门双轴的同步控制.加入模型补偿的控制器与LESO,一方面能够对已知耦合进行直接补偿,削弱耦合作用,另一方面能够对未知扰动和模型不确定性进行抑制,增强控制算法的适应性.上述控制模型和控制器设计都在广义坐标下进行,而实际龙门系统传感器所采集的位置信息和作用到龙门的驱动力均在笛卡尔坐标下,因此定义如下式所示的坐标变换进行转换.

(18)

3 试验结果与分析

基于自主搭建的龙门双驱运动平台和自主开发的龙门双驱伺服驱动器进行试验.龙门双驱运动平台的双驱轴采用雅科贝斯AUM3-S3并联型无铁芯直线电机,推力常数Kf=16.8 N/A,LAMOTION增量型0.1 μm分辨率(实际使用0.4 μm分辨率)光栅尺,横梁轴采用滚珠丝杠模组与永磁同步旋转电机的组合;龙门双驱伺服驱动器采用STM32G431系列微处理器作为主控,其中部署本文双驱解耦与同步控制算法与横梁轴单轴伺服驱动器通过控制器局域网总线(CAN)和自定协议进行通信;采集得到的数据由双驱伺服通过自定协议RS232通信传输至上位机,经上位机导出JSON格式数据文件后由MATLAB作图.

为验证自主搭建平台和设计驱动器的基本性能,保证试验结果一致性,首先对平台的重复定位精度进行测量.参照GB/T 17421.2—2016标准,使用中图SJ6000激光干涉仪,选取10 mm作为总测量距离,1 mm作为测量间距,往复运动5次,获得中图软件导出数据如图3所示.试验测得在10 mm行程内,平台双驱轴重复定位精度达到0.613 μm,可保证后续试验开展的一致性.

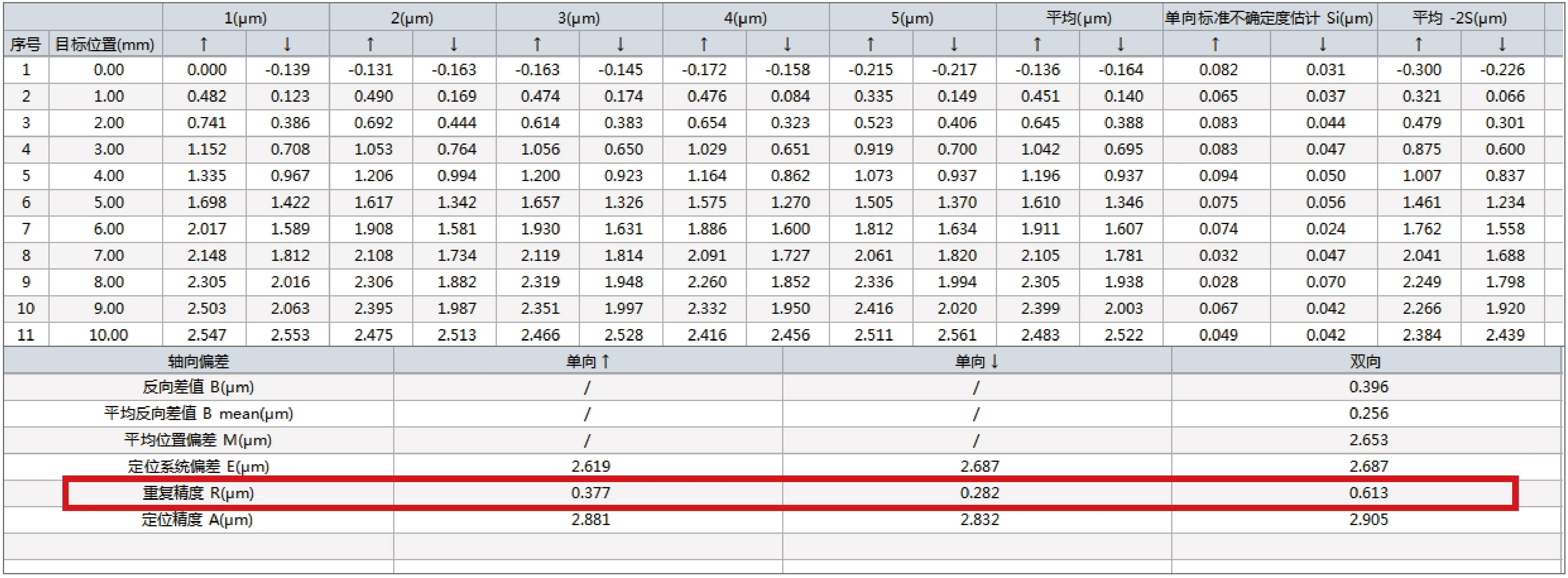
图3 使用中图SJ6000激光干涉仪测量的重复定位精度结果Fig.3 Test result of repeated positioning accuracy using SJ6000 Laser Interferometer

为验证平动速度环模型补偿ESO对提升龙门平动响应的效果,采用10 mm平动阶跃给定信号测试,对比龙门平台的响应如图4所示.可知在两种控制算法下平动响应的上升时间相同,均为0.06 s,但在接近目标值时两者的表现差异明显.由于龙门双驱系统通常应用于精密定位场合,所以选取系统稳态误差小于0.001 mm所需时间作为系统调节时间.在总移动质量超过50 kg的情况下,所提算法的调节时间为0.38 s,而无补偿比例-积分-微分(PID)控制器需要 0.66 s,二者相差接近2倍.值得注意的是,本文同样对有补偿PID算法进行了试验,其效果不及无补偿PID控制.为尽可能保证两种算法对比的公平性,仅改变速度环积分项的产生方式,即分别由模型补偿ESO和经典积分器产生,设置相同的限幅系数,保持其余控制参数不变.

图4 龙门试验台在不同控制算法下对阶跃平动位置信号的响应曲线Fig.4 Comparison of system translational step responses in model-compensated 2nd-order ESO control and non-compensated PID control

由广义坐标的定义可知,Xg和偏转角Θg共同决定横梁的位置,因此需要考察角度环的动态响应能力.大负载高惯量的龙门系统在两种控制算法下的角度环阶跃响应对比如图5所示,由图可知无补偿PID控制具有较短的上升时间,但其超调量和调节时间都远大于所提算法.以1 μrad误差作为调节时间指标,在1 mrad阶跃给定信号下,所提算法调节时间为0.473 s,而无补偿PID控制超过1 s,二者效果同样相差2倍之多.

图5 龙门试验台在不同控制算法下对阶跃转动角度信号的响应曲线Fig.5 Comparison of system rotational step responses in model-compensated 3rd-order ESO control and non-compensated PID control

在某些应用场景中,龙门双驱系统所装载的工作设备会与被加工物体直接接触,产生未知的外部扰动力,对定位精度产生影响,因此有必要验证控制算法对外力扰动的抑制能力.在实际试验中,难以产生能够迅速稳定的阶跃外部推力扰动,因此改变试验方法,先在X轴方向对系统施加100 N推力并等待系统位置稳定后,突然撤去该外部推力,测量两种算法的表现对比,如图6所示.可以看出,无补偿PID控制在突撤负载后有接近0.1 mm的位置移动,而对于所提算法这一数值不足0.06 mm.前者需要0.7 s重新恢复1 μm误差范围,而所提算法仅需0.45 s.由此可知,所提算法对阶跃外部推力扰动具有更强的抑制能力.

图6 龙门试验台在不同控制算法下对阶跃负载扰动信号的响应曲线Fig.6 Comparison of system responses in step load disturbance using model-compensated ESO control and non-compensated PID control

图7 龙门试验台在3种不同控制算法下对横梁轴负载余弦扰动的响应曲线Fig.7 Comparison of system responses in sinusoidal load disturbances using model-compensated ESO control, non-compensated ESO control, and non-compensated PID control

4 结语

本文所提出的基于模型补偿扩张状态观测器的龙门双驱解耦与同步控制算法,在自主研发的龙门双驱伺服驱动器上部署实现并在自主搭建的龙门试验台上取得了显著效果.主要创新点在于,首先,针对龙门双驱平台所使用的非对称柔性支撑结构特点进行龙门动力学建模,设计了平动和转动控制回路以解决平移和同步之间的矛盾,通过模型转换解决转动模态与平动模态的稳态耦合;其次,提取影响系统动态和导致回路间耦合的关键因素,对控制输出和经典线性扩张状态观测器的输入信号进行扩充,在不改变原有观测器极点配置和带宽设置的情况下,实现动态解耦和对内外扰动的补偿,提升了系统的动态响应和抗扰能力;最后,所提算法给出了针对柔性龙门双驱系统的一种通用解耦与控制框架,具有所需参数少、状态易于获取、算法复杂度适中等优点,易于工程部署实现.在后续研究中,将考虑通过非线性系统的有限时间控制策略进一步降低系统的调节时间,满足半导体领域等需要更高控制带宽的行业需要.