肠道机器人无线供能的混合式三维发射线圈特性研究

庄浩宇, 颜国正, 费 倩, 汪 炜, 赵 凯

(上海交通大学 电子信息与电气工程学院; 医疗机器人研究院,上海 200240)

随着研究的不断深入,胃肠道胶囊机器人(CR)[1-3]被赋予了诸如主动运动、药物释放、组织活检等功能,随之而来的是不断增加的能量消耗,可达到约570 mW[4],因而机器人的能量供给成为了机器人进一步发展的主要瓶颈[5].无线能量传输(WPT)技术已被证明可用于为生物医疗设备供电.近场WPT主要可分为非辐射下的电容耦合式、磁耦合感应式以及磁耦合谐振式[6],其中,磁耦合谐振式WPT利用发射侧和接收侧在中频(10 kHz～10 MHz)范围共振,能够有效地提高传输效率、延长传输距离,且该频段内生物组织中的场衰减可以忽略不计,因而成为研究的重点[7].

用于肠道机器人的WPT系统,面临以下挑战:① 具有主动运动能力的多功能CR具有直流电机、图像模块等器件,功率需求较高;② 能量接收线圈(PRC)与能量发射线圈(PTC)尺寸差异较大,且能量传输距离远,导致耦合程度弱,传输效率低;③ CR在肠道内的位置不固定,活动范围较大,因此需要PTC具有较为均匀的磁场范围;④ CR在肠道内的姿态不固定,因此需要WPT系统具有多维能量传输的能力.

为了解决单维PTC与单维PRC的形式无法实现空间多姿态充电的问题以及多设备同时充电的需要,空间全向WPT成为了研究的热门.文献[8]对三维正交线圈分别通入具有等相位差的3组相同大小的电流,以实现空间中的旋转磁场,然而这种方案被认为能量利用率较低,因为在同一时刻只有小范围内的磁场被有效利用.文献[9]中提出了使用单一电源供电的立方体形发射线圈,不需要相位和电流控制策略即可产生全向磁场,但仅仅验证了二维圆柱表面上的接收效果.

由于CR的特殊应用环境,当前的研究成果主要集中在单维PTC三维PRC的模式[10-12],然而三维PRC的形式决定了CR的体积无法进一步缩小,限制搭载更多功能模块的可能性,相比之下多维PTC与单维PRC的组合将更有利于CR结构的微型化与集成化.目前,针对CR的两维甚至三维PTC的无线能量传输系统仍处在研究的盲区.

提出一种相对简单的产生空间三维磁场的方案,设计一种结构紧凑的混合式发射线圈结构,不同于电流幅度控制、相位控制等复杂的控制策略,该结构仅使用单个电源驱动,利用二维线圈的旋转产生覆盖三维空间范围磁场的效果;对该发射线圈的特性进行了研究,证明了该方案的可行性.

1 肠道机器人的WPT系统

使用CR的胃肠道诊查系统主要由3部分组成:主动式CR、WPT系统和远程控制终端.图1展示了所设计的用于CR的WPT系统应用场景.能量从体外的PTC通过近场感应耦合传输到缠绕于CR内部的PRC,由于CR在体内的位置及姿态并不固定,传输距离较远,以及PRC和PTC的尺寸差异较大,导致能量传输为松耦合,耦合系数较小,传输效率较低.PRC侧接收到的交流感应电压经过全桥整流,稳压滤波后为负载供电.将CR搭载的图像模块采集到的视频信号通过射频传输到上位机终端,医生可以远程操控CR以实现各项功能.WPT系统的集总参数等效电路模型如图2所示.其中:PWM为输入的方波信号;Udc为直流电压;Ut为逆变电路输出的交变电压信号;It为发射侧电流;Ct为发射侧调谐电容;Lt为发射线圈电感;Rt为发射线圈等效电阻;Ir为接收侧电流;Cr为接收侧调谐电容;Lr为接收线圈电感;Rr为接收线圈等效电阻;RL为负载电阻;M为PTC和PRC之间的互感.

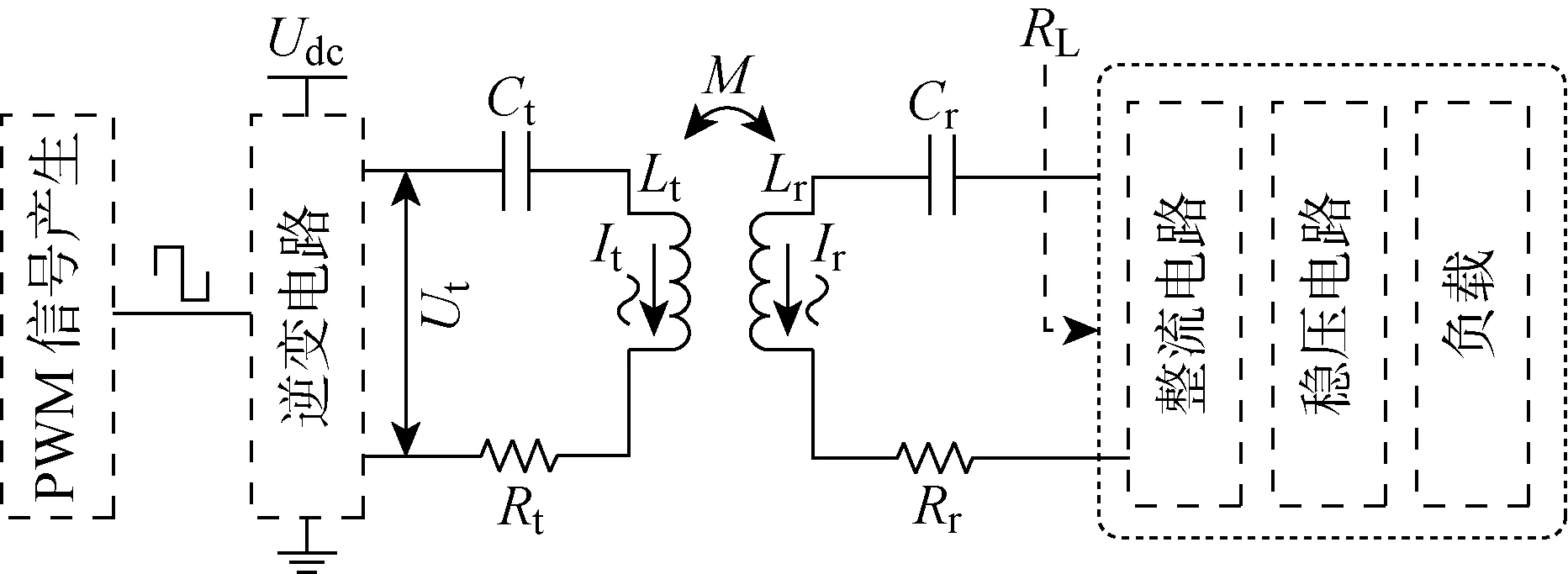
图2 用于CR的WPT系统的典型等效电路模型Fig.2 Typical equivalent circuit model of WPT system for CR

PTC和PRC之间的角频率为ω.对于松耦合的WPT,选择串联谐振补偿电路是因为其具有更好的负载性能[13].WPT系统的发射侧和接收侧分别通过调谐电容Ct(发射侧)和Cr(接收侧)进行补偿,谐振在相同频率以最大化传输效率(PTE).传输效率η是负载功率与发射功率之比,可通过下式获得:

(1)

Qt=ωLt/Rt

(2)

QrL=ωLr/(Rr+RL)

(3)

QL=ωLr/RL

(4)

式中:PL为负载功率;Pt为发射功率;k为发射线圈和接收线圈间的耦合系数;Qt为发射线圈品质因数;QrL为接收线圈带负载品质因数;QL为负载品质因数.

2 发射线圈建模

2.1 亥姆霍兹线圈对

亥姆霍兹线圈对(HCP)由通入同向电流的同轴对称放置的两个相同圆形线圈组成,并要求线圈之间的距离等于线圈半径,由于能产生相对均匀的磁场,所以被广泛用作PTC的典型结构.文献[14]中对亥姆霍兹线圈的均匀性进行了详细分析.HCP示意图如图3所示.在笛卡尔坐标系中任意点(x,y,z)上,N匝圆形线圈产生的磁感应强度BC(x,y,z)可根据毕奥-萨伐尔定律和叠加原理计算,可写成如下形式:

图3 HCP示意图Fig.3 Schematic of HCP

BC(x,y,z)=Bx,Ci+By,Cj+Bz,Ck

(5)

(6)

式中:r为线圈半径;I为线圈电流;μ0为真空磁导率;θ为线圈上某一点与x轴正方向形成的夹角;i,j,k为x,y,z轴所对应的单位向量.因此,对于每侧N匝对称放置的HCP,其磁感应强度表达式如下:

(7)

式中:Bx,HCP,By,HCP,Bz,HCP为HCP磁感应强度沿着x,y,z轴的分量.

2.2 鞍形线圈对

由于HCP要求线圈间距等于线圈半径,在一些对尺寸有限制的场合下缺乏灵活性和实用性,所以使用了一种新的PTC形式,即鞍形表面线圈对(SSCP),以产生与HCP磁场方向垂直的磁场,且该线圈形式可以与HCP有效组合,极大程度减小组合线圈的空间体积.SSCP示意图如图4所示.其中:a为SSCP的轴向宽度;b为鞍形线圈两直线边的距离;h为SSCP中两线圈的间距;θ0为SSCP所对应的中心角;BSSCP为SSCP产生的磁感应强度.SSCP由对称缠绕在圆柱表面上的一对鞍形线圈组成,其中具有相同方向的电流能够产生叠加的增强磁场.

图4 SSCP示意图Fig.4 Schematic of SSCP

BSSCP=BAB+BBC+BCD+BDA+

BA′B′+BB′C′+BC′D′+BD′A′

(8)

式中:Bmn为其下标对应的圆弧及线段的磁感应强度.但如此一来,计算表达式会变得冗长复杂,因此将采用数值仿真的方法进一步分析.

3 发射线圈特性分析

任一点(x,y,z)产生的磁感应强度Bi(x,y,z)相对于坐标系原点磁感应强度Bi(0, 0, 0)的不均匀性可定义为

(9)

i∈{x,y,z}

在本文中,HCP和SSCP的直径均设置为 600 mm,以容纳标准体型的成年人进入,并且可以保证与线圈有足够的距离.对于SSCP,两个重要的参数为纵横比α=a/(2r)以及中心角θ0.不同的纵横比和中心角会对磁场的均匀性产生影响[15].α=2和θ0=120°的组合理论上可以使得磁场均匀性最优,然而实际应用中,由于尺寸限制,该理想条件往往无法满足.在本文中,考虑到实际尺寸的限制,设置α=1.5,θ0=120°,SSCP磁感应强度不均匀性的数值仿真结果如图5所示,相同半径下的HCP的磁感应强度不均匀性如图6所示.其中:δx为磁感应强度沿x轴分量的不均匀性;δz为磁感应强度沿z轴分量的不均匀性.由于HCP和SSCP具有对称性,所以选择yOz平面作为测试平面.

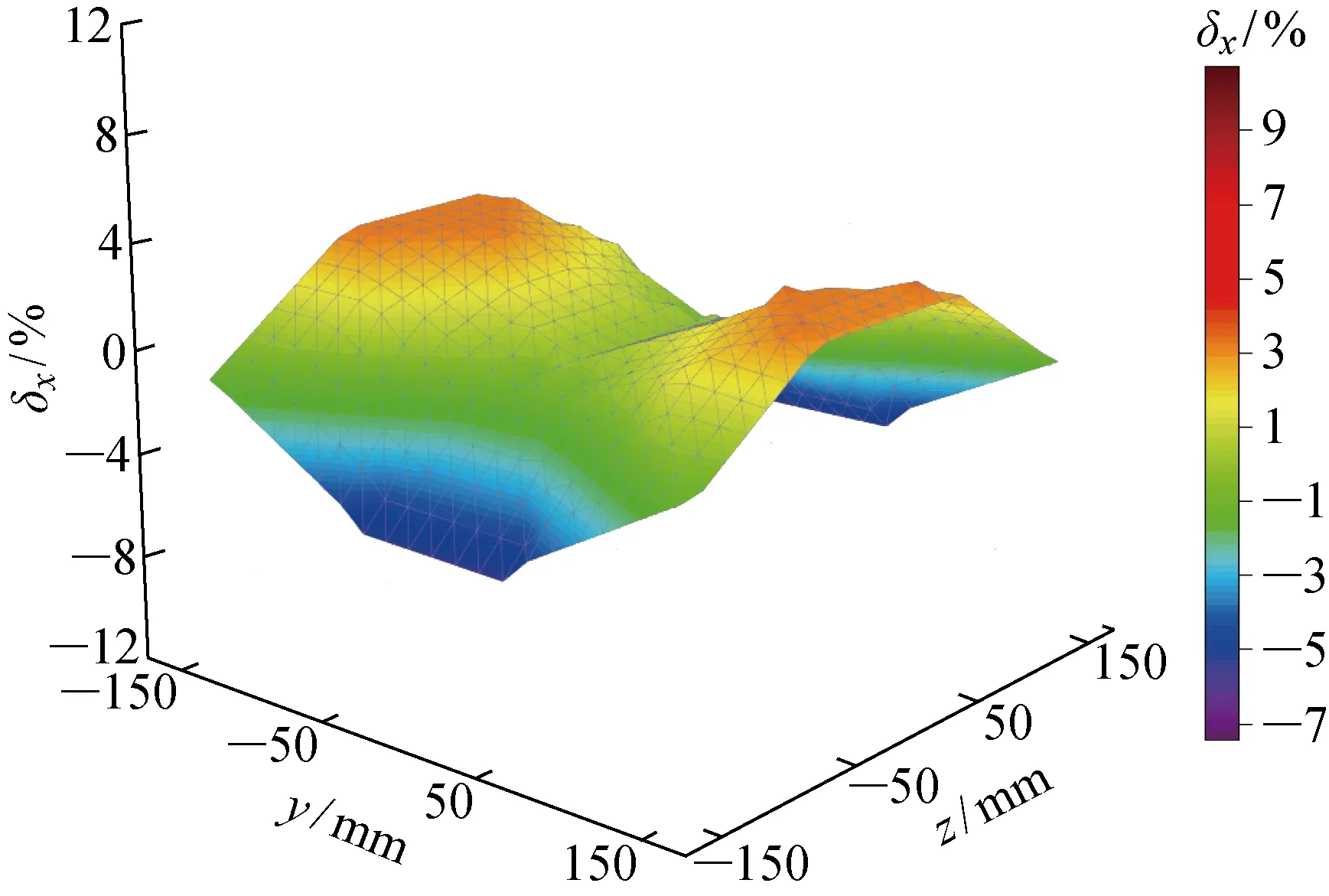
图5 SSCP在测试区域内的不均匀性仿真结果Fig.5 Non-uniformity simulation results of SSCP in the test area

图6 HCP在测试区域内的不均匀性仿真结果Fig.6 Non-uniformity simulation results of HCP in the test area

考虑到PRC可以在人体腹部约200 mm×200 mm 区域内自由移动,PTC应产生相对均匀的交变磁场,以确保PRC能够在不同位置接收到稳定的功率.因此,考虑到患者体型的差异和卧位的不确定性,测试区域被指定为300 mm×300 mm的范围.通过Maxwell的仿真结果可以得知,HCP测试区域的磁场分布呈现中部平坦,在靠近平面的4个角的位置出现较大起伏,而SSCP的磁场分布整体是波动的,但总体而言,SSCP的波动范围相对小于HCP.对于本应用来说,均匀性均在可以接受的范围内.

图7显示了在HCP和SSCP加载相同安匝数且相位相同的电流激励下的合成磁场.当发射线圈绕着z轴旋转,旋转角为φr时,不同旋转角下在中心点处沿着坐标轴向的磁感应强度分量如图8所示,其中:Bx、By、Bz分别为磁感应强度B沿着x,y,z轴的分量.从图8可以看出,若单维PRC轴向与x轴或y轴重合,则将PTC旋转直至SSCP产生的磁场方向与x轴或y轴对应重合的位置,将可以获得最高的传输功率;若PRC轴向与z轴重合,则在任意旋转角下,PTC传递给PRC的能量相同.

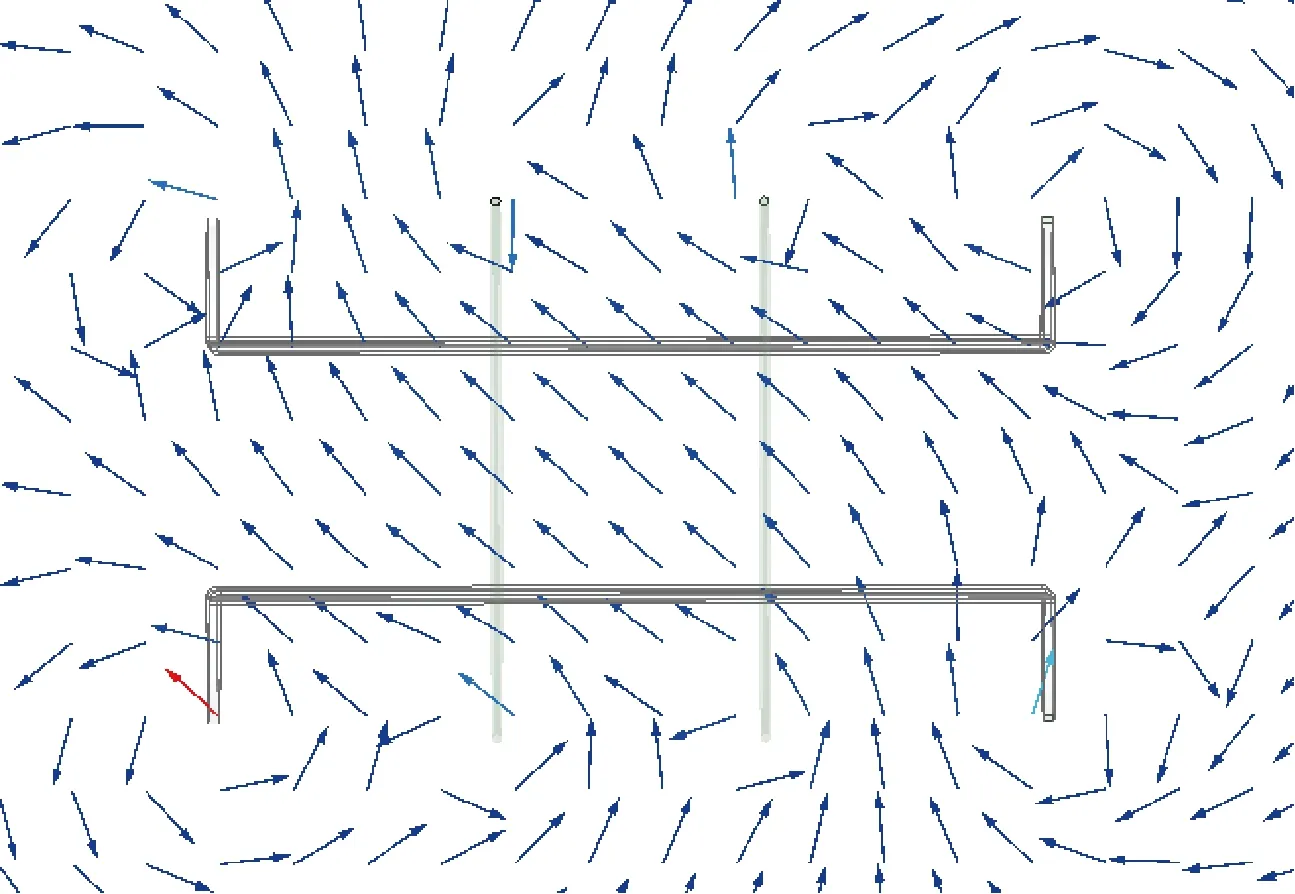
图7 相同激励下的合成磁场Fig.7 Synthetic magnetic field at the same excitation

图8 不同旋转角下沿坐标轴向磁感应强度Fig.8 Magnetic induction intensities along coordinate axis at different rotation angles

4 实验验证与分析

所制作的验证原型和实验设置如图9所示.为了减小趋肤效应和临近效应带来的涡流损耗,使用300股AWG44利兹线代替传统的实心铜线绕制了所提出的PTC的原型,HCP和SSCP的匝数均设置为30.利用所设计的三轴旋转试验台可以方便地实现PRC的三维角度变化.所有框架均由亚克力材料制成,以提供良好的绝缘性能.根据之前工作[16-18]中的实验经验,选择218 kHz作为较合适的谐振频率.测试的PRC为∅11.5 mm×11.5 mm的单维空心圆柱线圈,内侧附有锰锌铁氧体磁芯,以增强耦合.与文献[16,19]中所使用的类似,PRC的形状和大小使其适用于大多数的CR.在PRC的整流输出端串联一个典型值为21.6 Ω的负载电阻以模拟实际运行时CR的等效负载.根据仿真结果,将HCP和SSCP的驱动电流设置为2 A.

图9 制作的验证原型和实验设置Fig.9 Implemented prototype and experimental setup

首先,分别对HCP和SSCP的位置均匀性和角度均匀性进行了测试,接收电压均匀性可以通过负载接收电压的均匀系数评价,并可以通过类似式(9)的方式定义:

γL(x,y,z,φ)=

(10)

式中:γL(x,y,z,φ)为负载均匀系数;UL(x,y,z,φ)为任意点任意偏移角下的负载接收电压;φ为偏移角,是PRC的轴向与z轴正方向所成的夹角;φ0为参考角,始终保证PRC的轴向处在xOz平面内,且混合线圈没有发生旋转,即PTC的旋转角φr为0.对于HCP和SSCP,沿着x,y,z轴的位置均匀性被分别测试,接收电压和位置均匀性如图10和11所示.由图10可知,PRC的轴向始终平行于z轴,意味着没有角度偏移(φ=φ0=0°),同样由图11可知,PRC的轴向始终平行于x轴(φ=φ0=90°).对于SSCP,y轴上的位置均匀性优于其他两个轴,并且沿x轴和z轴呈现相反的趋势,位置均匀性的最小值为88.1%.在SSCP的中心,输送至负载的功率(PDL)达到 1 204 mW,PTE为3.44%.对于HCP,位置均匀性的最小值为92.2%.在HCP中心,PDL达到 1 341 mW,PTE为4.16%. 将HCP和SSCP串联,使用单个直流源在2 A的激励下,PRC在不同偏移角下的接收电压如图12所示,在接近45° 的位置能够获得最大的接收电压.

图10 HCP的接收电压和位置均匀性测试Fig.10 Receiving voltage and positional uniformity test for HCP

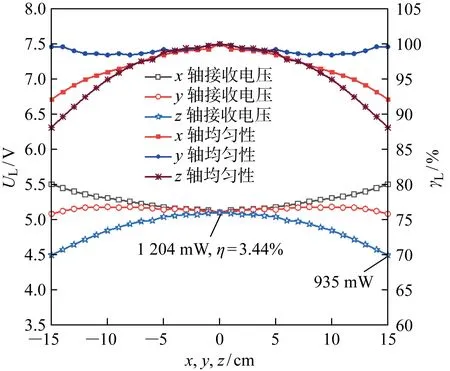
图11 SSCP的接收电压和位置均匀性测试Fig.11 Receiving voltage and positional uniformity test for SSCP

图12 不同偏移角下的接收电压Fig.12 Receiving voltage with different angular offsets

5 结语

提出一种用于肠道机器人的新型混合式三维发射线圈结构,通过特性分析和实验表明,本文所提出的PTC形式可以产生较为均匀的多维度空间磁场.由于结构的对称性,结合绕轴向的旋转,使用单个独立电源即可实现二维平面磁场到三维空间磁场的扩展,并且具有紧凑简单的线圈结构,不占用空间.其亦可通过使用电流以及相位控制的方式实现特定方向的磁场或者旋转磁场的效果,具有较好的适用性和应用前景.