含电能路由器的配电网转供灵活性量化分析

张 蓬, 吕恭祥, 刘志杰, 朱守真, 邵智勇

(1. 北京智中能源科技发展有限公司,北京100083;2. 清华大学 电机工程与应用电子技术系, 北京100084)

21世纪以来,全球能源供应日益稀缺,传统能源造成的环境污染在世界范围内也越发严重.为了优化能源结构,以光伏和风力发电(简称风电)为代表的可再生能源越来越多地接入到电力系统中.然而,由于这种可再生能源具有波动性和不确定性,当其占比较高时将严重威胁配电网的安全稳定运行.因此,电力系统需要提高协调灵活资源和调节运行状态的能力,即对内部或外部不可预测变化的应变和响应能力[1].

2008年,国际能源署正式给出电力系统灵活性的明确定义.电力系统的灵活性是指电力系统在其边界约束条件下,对可以预见和不可以预见的变化与事件迅速反应,在负荷需求减少时减小供应、负荷需求增加时增加供应的能力[2].

基于以上定义,进一步发展出配电网灵活性的定义.配电网灵活性指在不同时间尺度下,对外界分布式电源(DG)大规模接入与负荷种类多元化的应对能力[3].这种情况下如果配电网能够快速响应大幅度波动,在保障运行经济性的同时能够保证安全性与稳定性,则灵活性足够好[4-5].

转供灵活性是指采用网络重构、DG接入、电能路由器(EER)控制等调节措施之后,变电站或配电网对电能的传输与调度能力[6].转供灵活性有两部分来源,分别为站内转供与站外转供.站内转供为某一个变电站内部变压器之间进行负荷转供,站外转供为两座及以上变电站之间进行转供.站内转供能力主要从过载的角度来衡量,如过载持续的时间长短和主变的具体过载系数;而站外转供能力可以用两变电站之间可以转供的负荷来衡量[7].由于网络重构既包含变电站内部联络线的断开与连接,也包括变电站两两之间联络线的断开与连接,同时DG和EER都可以通过对潮流的控制来影响变电站内外的转供情况,这两种转供能力是相互关联、相互影响的,所以本文将两种转供能力作为一个整体考虑,即转供灵活性.文献[8]中针对网络重构和DG的接入,在考虑典型的负荷断面情况下,求出特定配电网与主网交换功率潜力的极限值,从而进一步计算转供灵活性.

EER是新兴的智能化电器连接装置,其建成的基础与关键在于电力电子技术的突破和信息技术的发展,它能够统一调控各种DG功率供给情况与储能单元的充、放电状态,使其能够与配电网更好地协调,更安全、稳定、经济、灵活地向负载供电.EER的基本架构包括通信单元、控制单元与功率单元3个部分;EER的发展过程经历了高频变压、全电子化变压、智能高频变压、高压高频变压和多端口路由变压5个阶段;EER使用的关键技术包括变换单元组合技术、端口即插即用技术、协调控制技术、分级通信技术和分层能量管理技术.文献[9]中设计了EER的拓扑结构,分析了EER的控制策略.文献[10]中在考虑不同拓扑结构的损耗情况下,研究以EER为核心的交直流配电网潮流计算方法,建立包含定电压、定有功、定无功、下垂控制等多种控制方法的EER统一控制方程.文献[11]中则提出一种适用于简化电能路由器的改进支路潮流模型,用于配电网的最优潮流计算,但模型过于简单,没有充分体现EER的功能.

考虑到EER灵活性的本质在于有目的地传输与转供能量,已有文献提及并描述配电网的转供能力,但缺乏具体计算方法.本文首先提出考虑网络重构、DG、EER的配电网转供灵活性这一评价指标及其计算方法;其次,基于二阶锥松弛的配电网最优潮流基本模型,结合EER的线性化模型,定义相应目标函数和约束条件,构建描述配电网转供灵活性的数学模型.最后,基于94节点理想配电网模型,对比可调度DG、不可调度DG以及接入EER等不同场景下的计算结果,分析探讨不同DG运行情况、EER的端口容量等因素对配电网转供灵活性的影响.

1 转供灵活性的建模方法

1.1 转供灵活性评价指标

在配电网中,由于网络重构、DG等的影响,考虑典型负荷断面的情况下,某一个变电站和与之相连的主网进线端口交换功率存在一个可调范围[12].交换功率之所以可调,本质上是因为同一个配电网中,变电站内部以及不同变电站之间可以进行负荷的转供.EER最直观、最核心的影响也在于电能传输与转供.在此基础上,提出配电网转供灵活性的概念及其具体计算方法,分析相关影响因素.

首先,利用基于支路潮流模型混合整数二阶锥规划的最优潮流算法计算出每一个变电站交换功率的极限值,即在考虑使电网损耗尽可能小的情况下,求出变电站供给有功功率极限情况下的最小值与最大值.利用权重系数将多目标优化问题转化为单目标优化问题.其次,根据最优潮流计算得到每座变电站供给有功功率的最小值与最大值,从而得出单座变电站的转供灵活性.

Ei=Pmax, i-Pmin, i

(1)

式中:Ei为第i个变电站的转供灵活性;Pmax, i、Pmin, i分别为第i个变电站的最大、最小供给有功功率.根据每一座变电站的交换功率范围得到各自的平均交换功率,求和得到整个配电网与主网的平均交换功率,每个变电站的平均交换功率占配电网平均交换功率的比例即为加权的权重系数.根据每一个变电站的转供灵活性,采用加权的方式得到配电网整体的转供灵活性.

(2)

(3)

(4)

1.2 二阶锥规划

二阶锥规划是线性规划的衍生理论,已经被应用于博弈论、经济等多个领域,目前二阶锥规划的求解技术已经相当成熟,采用原对偶内点法等算法和商业算法包求解基于二阶锥规划的最优潮流问题,都有较好的效果.二阶锥规划是凸规划的一种特殊形式,因此具有凸规化所有的特征,即求解二阶锥规划能获得唯一全局最优解.

二阶锥规划的标准形式如下:

min{ETx|Zx=z,xi∈K,i=1, 2, …,N}

(5)

式中:变量x∈RN,z∈RH,E∈RN,Z∈RH×N;K为二阶锥或旋转二阶锥.

利用二阶锥松弛的技术可以求解最优潮流问题.具体方法如下:首先选择含DG配电网且使有功损耗最小的最优潮流模型;然后在建立模型约束条件的基础上,加入可控单元的约束条件以及改进后的辐射状网络约束;最后利用二阶锥松弛方法转化模型并对其求解.支路潮流模型为非线性规划模型,模型及约束条件中包含二次项和整数项,因此首先引入锥优化变量将其转化为二阶锥规划模型,当非线性问题转化为线性问题后可进行高效求解.

1.3 变电站交换功率范围优化模型

1.3.1目标函数 目标函数在求取最大值和最小值的时候分别有不同的形式,如下所示.

(6)

(7)

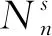
针对该目标函数的约束条件,以下重点介绍潮流约束和EER约束.后续仿真算例中使用辐射状约束、DG约束和安全约束[12].

1.3.2潮流约束 对于节点功率平衡约束,每个节点的有功功率和无功功率流入大小和流出大小都必须保持一致.

(8)

(9)

Pin,i=Pdg,i+Ps,i-PL,i

(10)

Qin,i=Qdg,i+Qs,i-QL,i

(11)

式中:Pin,i为节点i注入的有功功率;Pik、Pij分别为节点i流向节点k、节点i流向节点j的有功功率;b(i)、f(i)分别为节点k、j的范围;Pdg,i为DG提供的有功功率;PL,i为有功负荷;Qin,i为节点i注入的无功功率;Qik、Qij分别为节点i流向节点k、j的无功功率;Qdg,i为DG提供的无功功率;Qs,i为变电站节点提供的无功功率,若不是变电站节点则此值为0;QL,i为无功负荷;xij为线路的电抗.

式(12)是对线路的电压电流关系约束进行相角松弛的形式,即

(12)

式中:Vi、Vj分别为节点i、j的电压.

电流可由下式确定:

(13)

在考虑网络重构时,由于断开线路不满足式(11)的约束,需要对其采用大M法进行修改,根据电压幅值的限制选择一个比较大的数M,则有

(14)

(15)

由于式(13)包含变量的乘积项和二次项,所以需要将变量线性化,对其进行二阶锥松弛.这样,非凸可行域的问题将会松弛为凸二阶锥可行域.

(16)

二阶锥形式如下:

(17)

但在网络重构情况下断开的线路不满足该约束,需要引入中间变量,并用大M法约束:

(18)

(19)

(20)

式中:A、B为中间变量,是约束条件.

当线路断开时,对A、B相当于无约束;线路连通时,则与式(17)一致.

1.3.3EER约束 在考虑外特性的情况下,EER简化等效于多个交流-直流(AC-DC)转换器和DC-DC转换器的集成,如图1所示.图中:1、2、k、l均为输入电流的标号.

图1 EER简化等效结构图Fig.1 Diagram of EER simplified equivalent structure

如图2所示,以最小改造为原则将EER设置在交流配电网的某个节点上,如节点9,则该节点的参数将与EER该端口参数一致.由于节点间距离较远,每增加一个EER,其他端口需要与n个原系统中的节点通过联络线相连,增加了n个外部交流节点,如图中的N1、N2.同时EER内部的直流母线可以看作一个直流节点,内部的直流节点仅与EER内部的功率交换有关,将其视为与外部电网断开,配电网的相关约束与其无关.

对于外部节点,增加新的变量PE,i和QE,i,分别表示EER端口的接入节点和新增节点消耗的有功功率与无功功率,流向EER内部为正.除了EER新增的外部节点和接入节点以外的其他原始节点,这两个值均为0.此时其他约束条件同样适用于所有外部节点.新的功率平衡式为

Pin,i=Pdg,i+Ps,i-PL,i-PE,i

(21)

Qin,i=Qdg,i+Qs,i-QL,i-QE,i

(22)

AC-DC变换器两端的电压关系如下:

(23)

式中:VE,ij为EERi的交流端口j电压;Cij为VE,ij的电压调制系数;K′为电压调制比,取固定值;VDC为EER内部的直流母线电压.

DC-DC变换器两端的电压关系[13]如下:

(24)

式中:m′为DC-DC变换器变比;Rk模拟其损耗;Ik为直流端口流入的电流.

EER功率约束需要满足各个端口流入有功值的和为0,即EER只能对有功功率进行传输与转供而无法发出;EER的视在功率需要小于其装机容量;EER提供的无功补偿存在最小功率因数限制.则EER功率约束为

(25)

(26)

-PE,ijtan(arccosFE,ij)≤QE,ij≤

-PE,ijtan(arccosFE,ij)

(27)

式中:QE,ij为从EERi端口j流入内部的无功功率;SE,ij为EERi端口j的最大容量;FE,ij为EERi端口j的最小功率因数.

2 转供灵活性的仿真计算实例

进行实际计算评估分析所使用的交流配电网模型如图3所示.该配电网包含两座变电站,每个变电站均安装有两台变压器,T1和T2为变电站1的变压器,T3和T4为变电站2的变压器.该系统为94节点系统,共有94条支路,其中有11条联络线路(图中A-K所示)用于网络重构.交流电压等级为11.4 kV, 变化范围为标幺值下的0.95～1.05,配电网线路中所允许的电流最大值为500 A.每条支路的具体参数以及各节点的典型负荷见文献[14].

图3 94节点交流配电网模型Fig.3 Model of 94-bus AC distribution network

2.1 交流配电网基础转供灵活性

在此交流配电网中,考虑典型的负荷断面情况下,变电站1的有功负荷为16.430 MW,变电站2的有功负荷为11.920 MW.此时的转供灵活性来源于配电网自身的网络重构.

按照前文所述理论,首先利用最优潮流解法分4次求出各变电站供给有功功率的最小值与最大值,然后进一步求出各变电站供给有功的平均值与转供灵活性,最后可以得到配电网的转供灵活性,具体数据如表1所示,其中空白表示不适用.

表1 交流配电网转供灵活性Tab.1 Transfer flexibility of AC distribution network

通过以上计算,可以得出配电网的转供灵活性为8.757 MW.这个数据是改进前的配电网转供灵活性指标,将为后续分析奠定基础.

2.2 交流配电网接入EER对转供灵活性的影响

在最初交流配电网模型的基础上,在3条线路交汇的节点9、42、72处进行改动最小的改造,接入3台使用3个端口的EER.

由EER简化等效模型可知,此时配电网将变成100节点、94支路的模型,其中5条联络线路用于网络重构.同时改变EER每个端口的端口容量,变电站1、2以及配电网的转供灵活性变化情况如图4所示.

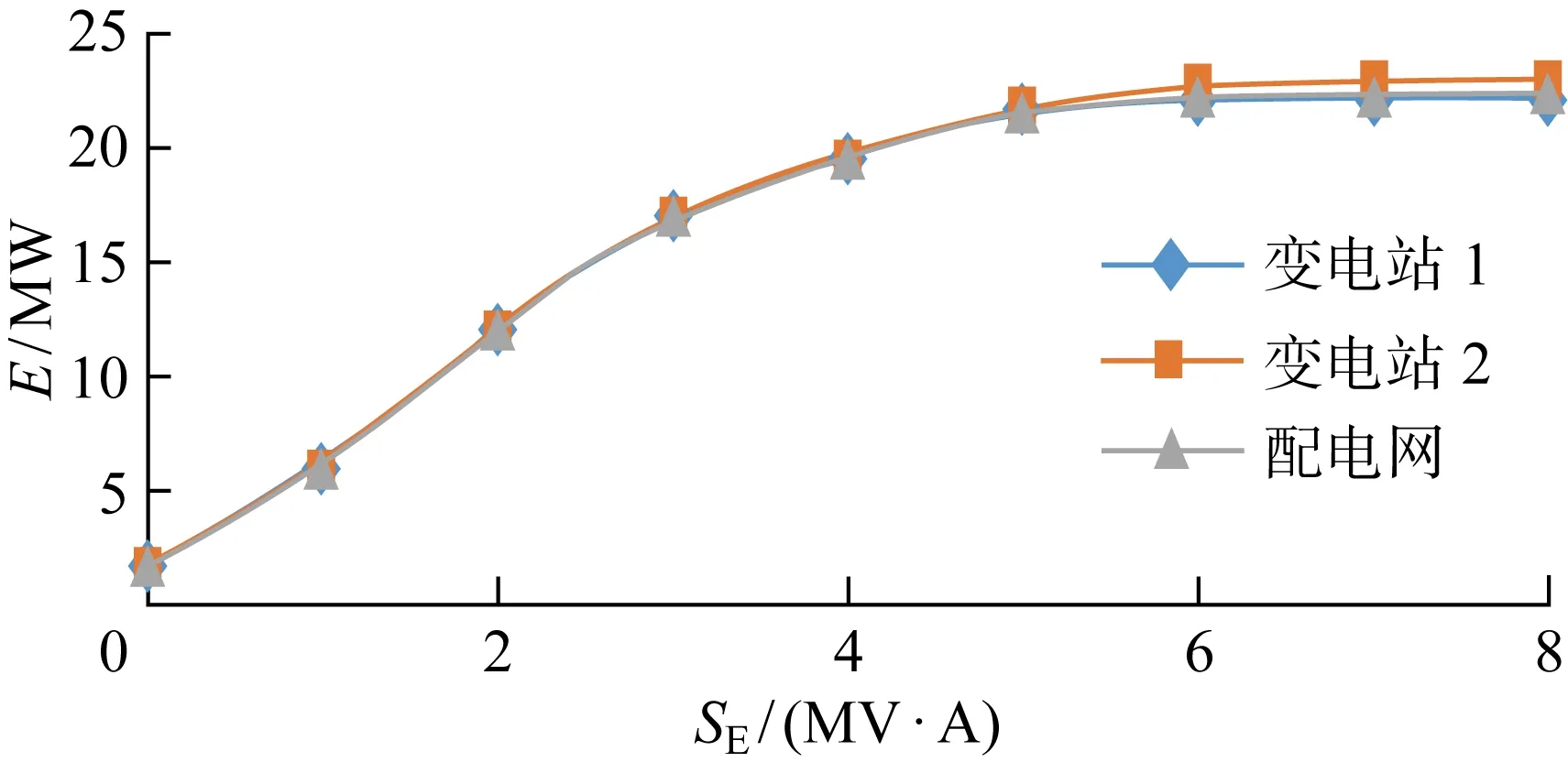
图4 配电网转供灵活性随EER端口容量变化图Fig.4 Variation in transfer flexibility with EER access

随着连接两座变电站的EER端口容量增大,配电网的转供灵活性也随之逐步提高.在端口容量达到6 MV·A后配电网转供灵活性基本不再改变,这是由于配电网其他支路容量、DG等参数限制了功率流动,此时单纯增加EER的端口容量已经无法进一步提高配电网转供灵活性.

EER对配电网转供灵活性影响巨大,在整个配电网有功负荷为28.35 MW时,EER能够将配电网转供灵活性从8.717 MW提高到22 MW.这一现象是多种因素综合作用的结果.第一,EER能够智能地调节控制各个端口的电压功率等相关参数;第二,EER自身带有无功补偿的能力,能够进一步优化线路的潮流大小与方向;第三,EER内部交流与直流相互隔离,即使两变电站通过EER形成电气连接,在网络重构的过程中仍然被认为是断开的,从而增强潮流流动的可选择性.

2.3 交流配电网接入可调度DG

在交流配电网模型的基础上,在节点 6、7、12、20、21、75、79、80 中接入可调度的DG,DG的装机容量为1 MV·A,最小功率因数为0.85.逐步提高可调度DG的最大出力水平,配电网的转供灵活性的变化情况如图5所示,其中δ1为可调度DG最大出力水平.

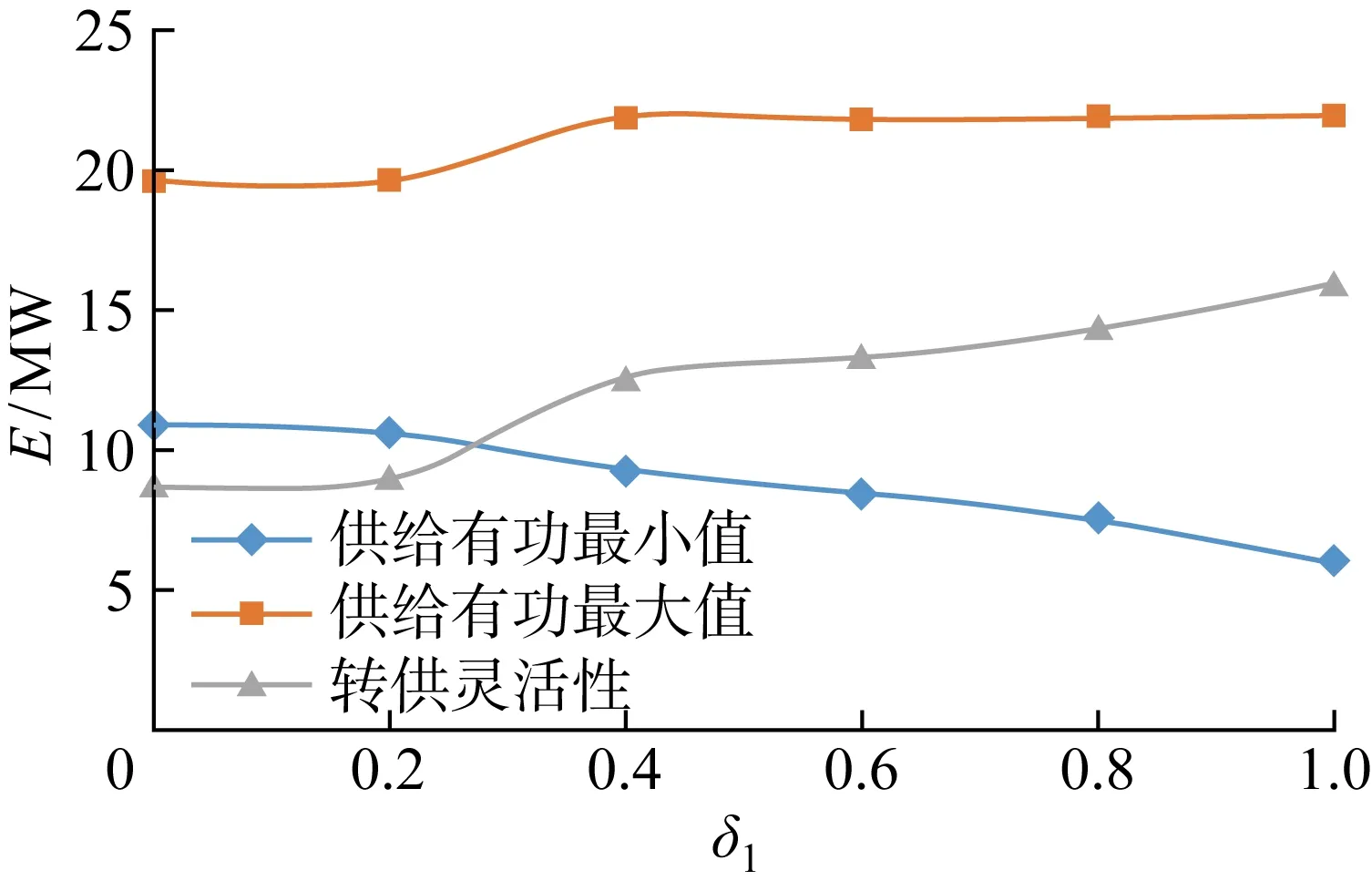
图5 DG容量变化对转供灵活性影响Fig.5 Impact of DG capacity change on transfer flexibility

在相应节点接入可调度DG后,随着其可调度的最大出力水平增加,变电站1和变电站2的供给有功功率最小值Pmin,i在不断变小,供给有功功率的最大值Pmax,i先增大后保持稳定.Pmin,i值变小的原因很直观——为保障可调度DG的出力增加,变电站需要减少有功功率的输出.而Pmax,i值变化是两方面因素综合作用的结果:一方面,变电站要尽可能增大有功功率供给,减小可调度DG的出力,甚至减小为0;但另一方面,可调度DG在有一定的出力情况下,又可以提高节点的电压幅值,这样让原本电压偏低的末端节点电压升高得以对另一变电站的其他节点进行转供.由于当前接入的DG是可调控的,所以随着最大出力水平的提高,最大出力水平更小时的极限在提高后依旧能够达到.后续转供灵活性不再提高,说明此时的配电网已经由于可调度DG的接入,潜力提升到极限.

2.4 交流配电网同时接入EER和可调度DG

在交流配电网中同时接入EER和可调度DG,分别选取端口容量为2和6 MV·A的EER探究可调度DG对灵活性影响,这是因为2 MV·A的EER改造代价比较小,同时能使转供灵活性高于原始的交流配电网,而6 MV·A的EER可以使配电网转供灵活性提升到极限.

配电网转供灵活性的变化如图6所示.EER端口容量分别为2和6 MV·A.可见EER能够显著提高转供灵活性,端口容量越大,改善效果越明显.

图6 配电网转供灵活性变化的对比Fig.6 Comparison of transfer flexibility between distribution networks with different schedulable DG access

2.5 交流配电网同时接入EER和不可调度DG

在交流配电网中接入不同端口容量的EER和不可调度DG,即输出固定的DG,对比分析配电网转供灵活性的受影响情况.

当配电网接入的不可调度DG的装机容量为1 MV·A 时,随着其波动范围的不断增大,配电网转供灵活性整体上逐步下降.配网中接入EER的端口容量为2 MV·A,其配电网转供灵活性变化如图7所示,其中δ2为不可调度DG出力水平.随着不可调度DG出力水平波动范围不断增大,两变电站及其整体配电网的转供灵活性不断降低,且两变电站之间的转供灵活性差距也不断增大.

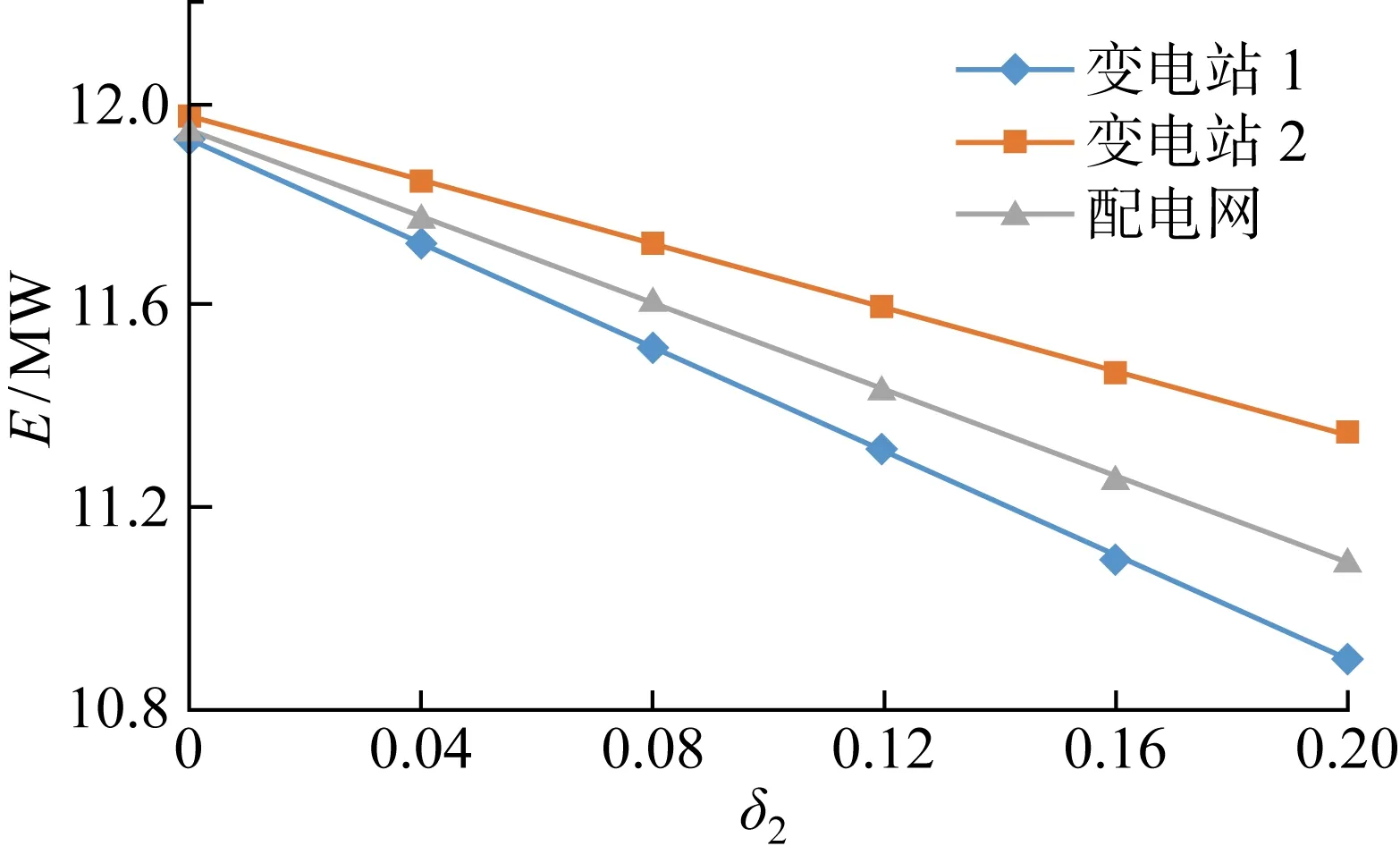
图7 含EER(2 MV·A)和不可调度DG(1 MV·A)配电网转供灵活性变化Fig.7 Variation in transfer flexibility of distribution network with EER (2 MV·A) and unschedulable DG (1 MV·A)

当配电网中接入的EER端口容量提高到6 MV·A 时,其配电网转供灵活性的变化如图8所示.可知,随着不可调度DG出力水平波动范围不断增大,两变电站及其整体配电网的转供灵活性都不断降低.当EER端口容量为6 MV·A时,两变电站之间的转供灵活性差距初始就较大且保持相对稳定.这是由于当EER的端口容量为2 MV·A时,对两变电站转供灵活性的影响差异还未达到极限,所以不可调度DG的波动还将继续增加这一差异;而当EER端口容量达到6 MV·A时,即使不可调度DG没有可再生能源的波动,也已经将两变电站转供灵活性的差异放大到极限.

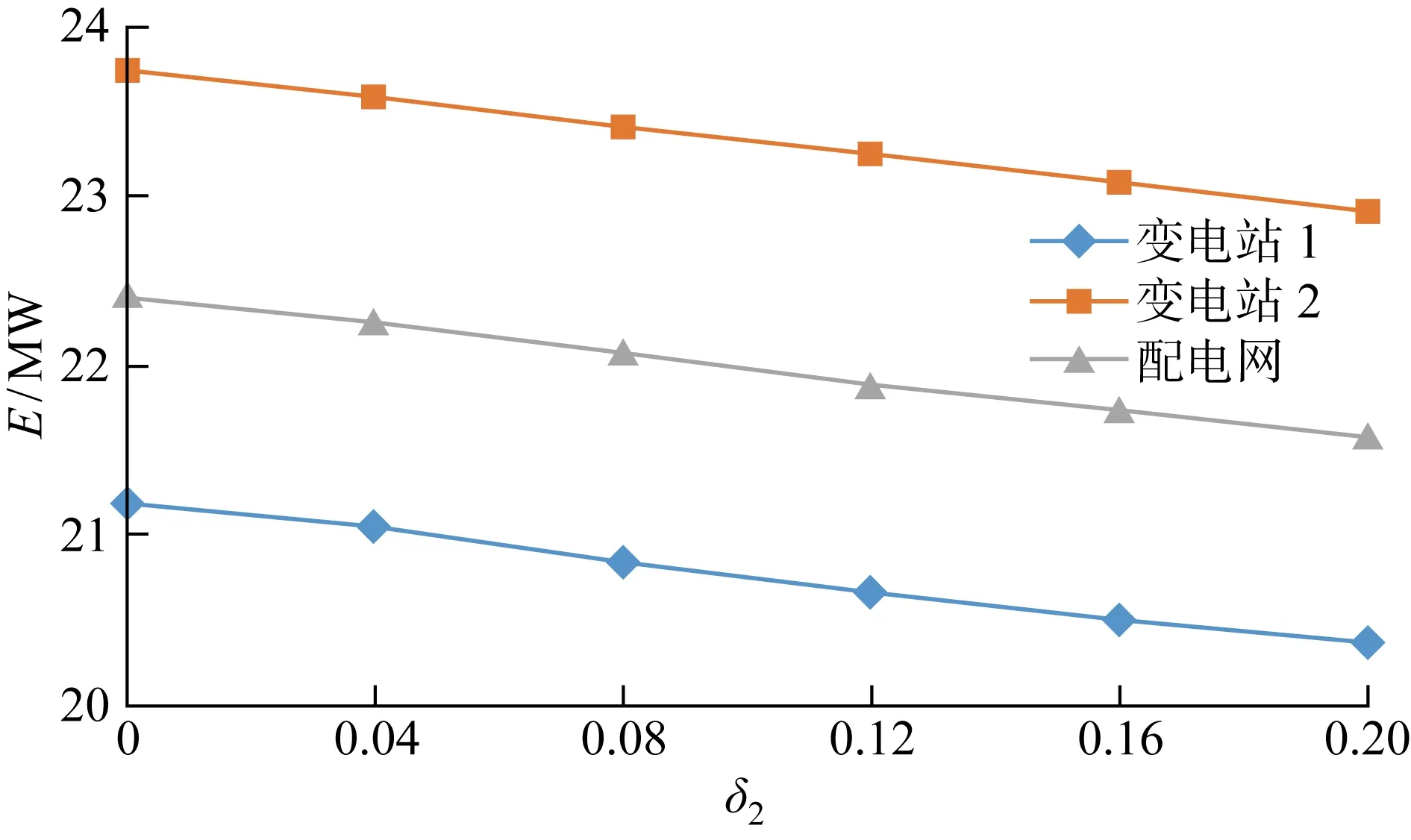
图8 含EER(6 MV·A)和不可调度DG(1 MV·A)配电网转供灵活性变化Fig.8 Variation in transfer flexibility of distribution network with EER (6 MV·A) and unschedulable DG (1 MV·A)

3 结语

从EER外特性出发,建立简化等效模型,同时考虑网络重构和可调度与不可调度的DG,提出含EER的配电网转供灵活性评估方法,研究结果表明:在交流配电网单独接入可调度的DG可以提高配电网转供灵活性;端口容量配置合理的EER接入配电网,能够显著提高含DG的交流配电网的转供灵活性.同时,EER能够遏制不可调度DG接入产生的波动性所造成的转供灵活性降低;EER端口容量越大,改善效果越显著,且两变电站之间的转供灵活性差距越大.

本文所提含EER的配电网转供灵活性评估方法和对算例的具体研究分析思路以及得到的相关结论都有很好的应用前景,可以在配电网改造、EER配置规划等项目中提供参考.

致谢国网北京电力公司对本项目也有部分资金资助.