盆架状压电宏微平面作动器半解析性理论建模
2023-05-31王哲逸贺红林龙玉繁李晨捷
王哲逸,贺红林,李 冀,龙玉繁,李晨捷
(南昌航空大学 航空制造工程学院,江西 南昌 330063)
0 引言
压电宏微平面作动器作为一类基于压电材料逆压电效应的新型动力部件,将电激励转换为定子微观振动,并通过定/动子间界面摩擦将振动转化为宏观移动[1-4],其响应快,运动精度高,工作平稳,断电自锁,在生物医疗、芯片制造等有高精定位需求行业中应用前景广宽[5]。Polit Sebastian等[6]提出一种具有纳米级分辨率的压电驱动平台,该平台的x、y向驱动行程可达15 μm,行进间位移分辨率可达1 nm;张军涛等[7]设计出一种精密二维定位平台,该平台将两向驱动耦合成50 mm×50 mm行程,定位精度为0.28 μm。本文提出了双十字形、田字形和口齿式等多种新构型[8-10]。在已有工作基础上,本文提出一种基于定子杆纵、弯复合振动的盆架状作动器,该作动器利用压电陶瓷d31效应激励工作模态[11]。压电作动器驱动特性主要取决于定子振动,故定子机电动力学分析尤为重要。已有研究主要采用有限元法,即将定子离散为众多小单元,通过联立各单元的力学平衡方程来构建定子总体线性动力学方程组[12-13]。但这种方法对网格依赖性大,且单元网格划分越细,定子节点越多,这将导致计算矩阵维度增加,从而降低计算效率。与有限元法相比,传递阵法是基于离散思想的结构力学特性分析方法,能清晰反映每一个状态变量的变化过程,是一种显式计算方法[14-15]。因其计算过程中独有的频率计算行列式阶次低,利于编程和数值计算等特点,常应用于结构力学计算[16-17]。此外,传递阵模型计算量少,解算速度快,内部状态显示清晰,能解决有限元模型无法解析化问题,特别是利用该法分析定子动力学特性时,能有效展示机电耦合力学传递行为[18-19]。为高效解算盆架状定子动力学特性及便于定子结构动力学优化,本文探析了盆架状定子的传递阵法建模及求解。
1 作动器结构及其驱动机理
1.1 作动器的动力学拓扑
根据宏微平面作动器两自由度运动需要,结合作动器纵-弯复合模态驱动的初始规划,提出的作动器动力学结构如图1所示。该作动器主要由4根驱动杆及1个十字架连接而成。在各杆中心处均钻通孔,以降低杆的刚度,有利于增大杆的振幅。各杆顶端驱动足推动动子。在十字架中心处设置通孔固定作动器。作动器共配置16片压电陶瓷片,其中位于各驱动杆最大应变处的8片陶瓷用于激励杆的纵振,弯振模态波峰(谷)处贴有8片陶瓷以激励杆的弯振。
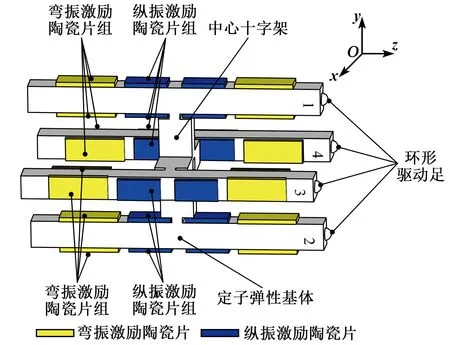
图1 盆架状超声作动器构型图
1.2 作动器的驱动原理
该作动器采用压电陶瓷片的LE模式,基于d31效应激发作动器工作振动,通过纵振与弯振的谐振耦合促成质点椭圆运动轨迹,以推动动子移动。图2为盆架状作动器在一个运动周期内的工作过程。图中,对弯振激励陶瓷片沿厚度方向极化,并施加正弦激励信号,纵振激励陶瓷片极化方向同为厚度方向,但相对的陶瓷片极化方向反向,并施加余弦激励电信号。当作动器的对称弯振模态被激发后,其驱动足将沿x、y向振动;当反对称纵振模态激发后,驱动足将沿z向振动。两模态的谐振在驱动足上耦合形成了两相微观椭圆运动轨迹。在每个周期内,1、2号杆和3、4号杆上的驱动足各完成一个椭圆轨迹运动,4个驱动足交替推动动子沿x、y向移动。
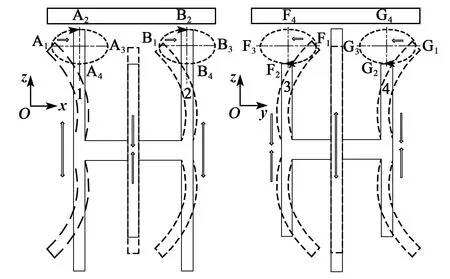
图2 驱动足运动过程
2 基于传递阵原理建模
根据压电学,压电陶瓷的d31压电效应可通过机电耦合方程描述,即:
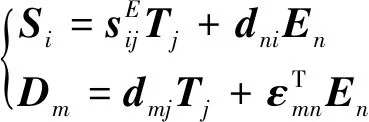
(1)
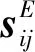
为简化作动器理论建模并尽可能准确反映作动器动力学行为,对作动器建模时假设:
1) 忽略压电陶瓷片与驱动杆间胶层的影响。
2) 作动器振动时,各平行截面保持平行,忽略驱动杆的扭转。
3) 杆纵振时,忽略横向变形,杆内微元只做沿轴线方向运动,且在同一截面上应力一致。
4) 忽略作动器装夹对驱动杆振动特性影响。
基于这些假设并利用传递阵和子结构法,可将盆架状作动器离散为等截面梁、变截面梁、等截面管柱单元、压电合梁和压电复合管柱单元,从而可建立各单元纵振、弯振及复合振动传递阵。
2.1 作动器子结构纵振传递方程
根据等截面弹性梁的自由态波动方程和动力学关系,可构建出等截面梁单元纵振传递阵方程为
(2)

(3)
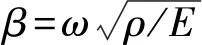
图3为管柱结构纵振。管柱单元的传递阵与式(3)类似,只是其截面积不同。
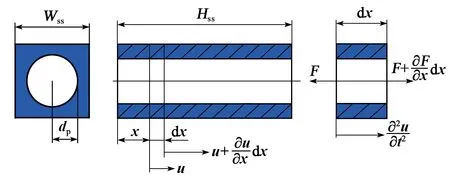
图3 管柱结构纵振
对于变截面梁,可先将其离散为n个等截面段,然后求各段的传递阵,最后将各段的传递阵进行连乘,可得变截面梁的传递阵为
(4)
式中Hs,Δxi为第i个离散段的传递阵。
压电陶瓷粘附于等截面梁后构成的压电复合梁如图4所示。当在激励陶瓷片上施加驱动信号时,可使压电复合梁纵向振动。考虑到陶瓷的纵振与梁的纵振趋于一致,故建模时可将梁和压电陶瓷片视作一体,则可得:
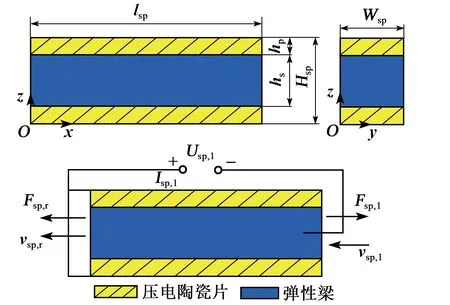
图4 压电复合梁纵振
(5)
式中:Tl,p,Tl,s分别为陶瓷片与弹性梁的应力;ρp,ρs,ρsp分别为陶瓷片、弹性梁和压电复合梁的密度,Sl,p、Sl,s,Sl,sp分别为陶瓷片、弹性梁和压电复合梁的应变;Γp,Γs为压电陶瓷片和弹性梁占整个压电复合梁的体积分数;ε33、s11、d31为压电常数、陶瓷片压电矩阵、介电常数分量。
根据压电复合梁的应力、应变关系,并考虑其电学和位移边界条件及其两端力与速度可得:
Fsp,l=Fsp(0,t)=Ssp(cspCsp,1ksp-
epUsp/hp)ejωt
(6)
vsp,l=vsp(0,t)=jωCsp,2ejωt
(7)
Fsp,r=Fsp(lsp,t)=Ssp[csp(Csp,1kspcos(ksp,lsp)-
Csp,2kspsin(ksp,lsp))-(epUsp,1/hp)]ejωt
(8)
vsp,r=vsp(lsp,t)=jω[Csp,1sin(ksp,lsp)+
Csp,2cos(ksp,lsp)]ejωt
(9)

Isp=2Wspjω[g1(Csp,1sin(ksplsp)+Csp,2cos(ksplsp)-
Csp,2)]ejωt+2Wspjω(g2lspUsp,1/hp)ejωt
(10)
联立式(3)~(10)可得压电复合梁单元传递方程:
(11)
(12)

压电复合管柱梁(见图5)的传递阵与式(12)相同,相关计算与式(5)相同,且纵振传递方程为
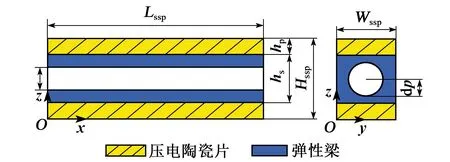
图5 压电复合管柱梁纵振
(13)
2.2 作动器子结构弯振传递方程
根据已有研究经验,利用铁木辛柯梁理论构建压电驱动杆的振动模型更合理。当将驱动杆划分为多段等截面梁单元时,可得:
(14)
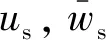
c4ejλ2sx/ls
(15)
引入欧拉式以改写式(12),并将其余3个力学参数Ms、Qs、ψs改写成相同格式,即有:
(16)
(17)
(18)
(19)
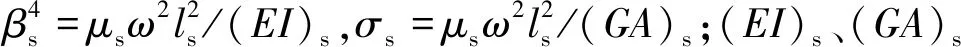
联立式(16)~(19)可得:
Zs=HsDs
(20)

考虑弹性梁两端存在如下边界条件,即:
(21)
式(21)消去Ds后可得:
(22)
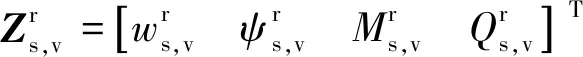
(23)
通过将变截面梁进行离散(见图6),可求取其弯振传递阵为
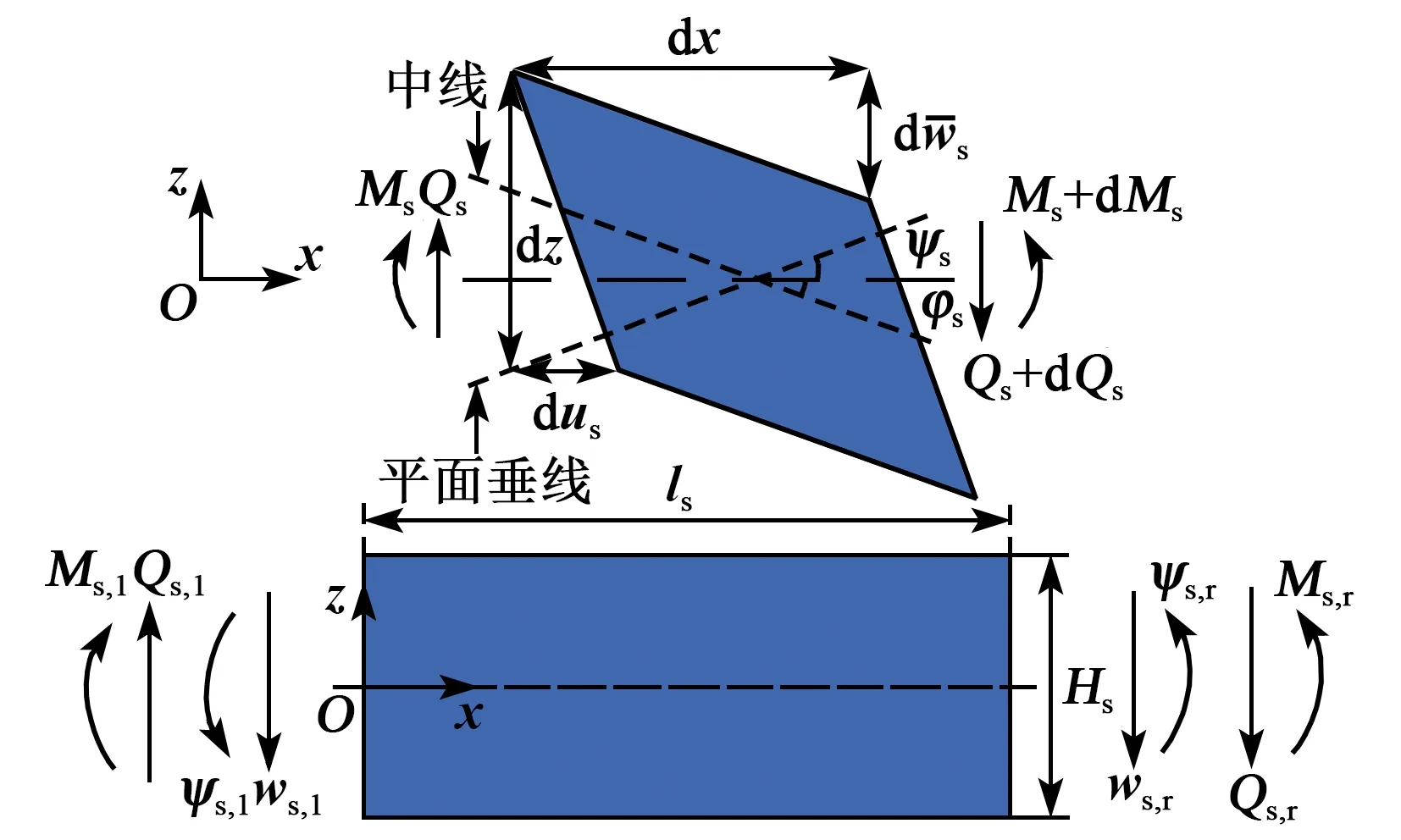
图6 弹性梁弯振
(24)
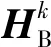
将变截面梁离散后,可得其弯振传递阵方程为
(25)
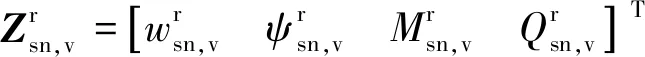
管柱梁同样具有式(23)的弯振传递阵形式,只是其刚度、质量和惯性矩须按下式求取,即:
(26)
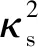
压电复合梁同样可视为铁木辛柯梁,当在压电复合梁上施加驱动电压时,将激励出纯弯振动,且其同样具有以下动力学特性,即:
(27)
式中:S1,sp为压电复合梁x向应变;S5,sp为压电复合梁的剪切应变。
图7为压电复合梁弯振。对压电复合梁单元做力学分析可得:

图7 压电复合梁弯振
Qsp-ω2ψsp(ρI)equ,sp
(28)
-ω2uZmequ,sp
(29)

联立式(28)、 (29)可得关于Msp和Qsp的微分方程,运用式(16)的解法可得微分方程特征根为
(30)
式中(GA)equ,sp,(EI)equ,sp分别为压电复合梁等效剪切刚度和等效弯曲刚度。
描述压电复合梁弯振模态的4个参数形式:
(31)
(32)
(33)
2αsphspUsp,2
(34)
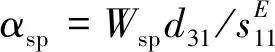
当激励压电陶瓷时,陶瓷将产生变形并引发电流为
Isp,2=jωCspUsp,2+2αsphp(ψ(x=lsp)-
ψ(x=0))
(35)
式中Csp=2Wsplspg2/hp为压电复合梁电容。联立式(31)~(34),可求得弯振传递阵为
(36)

(37)
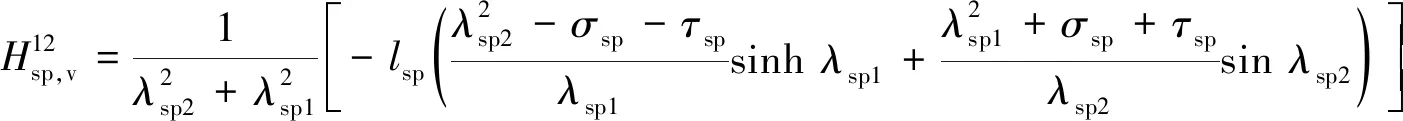
(38)
(39)
(40)
(41)
(42)
(43)

(44)
(45)
(46)

(47)
(48)
(49)
(50)
(51)
(52)
(53)
(54)
(55)
(56)
(57)
(58)
(59)
(60)
(61)
可见,压电复合梁传递阵中包含了力、电及机电耦合参数,利用这些参数可构建其传递方程。
压电复合管柱梁传递阵、传递方程形式与压电复合梁相同,只是其刚度、质量和惯性矩的表达式略有不同。压电复合管柱梁弯振传递方程为
(62)
2.3 作动器子结构弯-纵复合传递方程
盆架状作动器选定纵-弯复合模态为工作模态,因此还须构建驱动杆纵-弯复合传递阵。考虑到前文推导的等截面梁单元、管柱单元和变截面梁等非压电复合梁的纵、弯传递阵彼此独立,故可按以下方式构建纵-弯复合传递阵,即
(63)

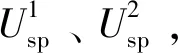
(64)
由此可得压电复合梁的传递阵方程:
(65)
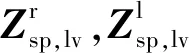
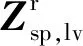
(66)
结合式(65)、(66)可得压电复合梁在纵-弯复合模态下的机电耦合动力学传递方程:

(67)
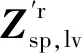
3 作动器机电耦合理论模型
以作动器十字架中心通孔作为固定端,将各驱动杆离散为单元(子结构),如图8所示。

图8 作动器子系统划分
基于振动在单元间传递的连续性,及在相邻单元连接面上存在合力为0与速度相等条件,结合前文推导出的各单元传递阵,将驱动杆上所有离散单元的传递阵进行累乘,便构建驱动杆传递阵。
3.1 子结构间复合振动连接条件
压电单元的纵-弯复合振动输入和输出状态向量中包含2个纵振力学参数、4个弯振力学参数及1个纵振电学参数等7个参数。作动器的相邻单元在纵弯复合振动时的界面连接条件如下:
1) 当结构振动由梁单元i传递至梁单元i+1时,二者纵-弯复合振动连接条件为
(68)
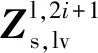
2) 当振动由弹性梁结构i传递至压电复合梁结构,两者纵-弯复合振动连接条件可写作:

(69)
(70)
(71)
3) 当振动由压电复合管柱梁结构传递至管柱梁结构,两者纵-弯复合振动连接条件可写做
(72)

4) 当振动由压电复合管柱梁结构传递至压电复合梁结构两者纵-弯复合振动连接条件可写做:
(73)

5) 当振动由中心十字架阶梯槽传递至驱动杆,形成压电复合梁结构i+1与压电复合管柱梁结构i+2的并联传递,三者纵-弯复合振动连接条件为
(74)
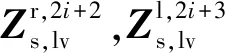
(75)
(76)
6) 当振动由阶梯槽传递至驱动杆管柱结构,形成弹性梁结构i+1与弹性梁结构i+2的并联传递,三者纵-弯复合振动连接条件:
(77)

3.2 机电耦合传递阵模型的构建
考虑到盆架状压电作动器为中心对称,为减少作动器整机机电动力学模型建模工作量,首先基于各子结构的弯-纵复合传递阵方程并结合子结构间的连接条件矩阵,将驱动杆与中心十字架相连,构造出单边机电耦合动力学模型;然后,考虑整机动力学分析模型的边界条件,构造完整的作动器机电耦合动力学模型。模型边界条件主要包括两方面:作动器驱动杆两端自由和中心十字架通孔处固定的机械边界条件;配置在压电陶瓷片上相位差为π/2的激励电信号的电学边界条件。驱动杆中任意一个离散元素有:
(78)
式中:BCAi为机械边界条件提取向量;BCBi为机械边界值向量;BCUi为电学边界条件提取向量;BCIi为电学边界值向量;Z2i-1,Z2i分别为离散元素i的振动输入和输出状态向量;Hi为离散元素i的振动传递阵。
综上所述,构造出作动器整体机电耦合动力学模型:
(79)
式中:Z1,Z2,…,Z2n为全体离散单元的输入、输出向量集合。左边矩阵上半部分表示各单元所对应的传递阵,中间部分为单元间连接条件,最下方为各离散单元边界条件提取矩阵。
4 作动器传递阵模型的验证
考虑到以子结构为基本要素的盆架状作动器传递阵机电耦合分析模型本质上是一个规模不大的非齐次线性方程组,故利用MATLAB编写程序以解算作动器机电动力学特性参数。为便于模型对比与确认,本文构建了作动器机电耦合有限元模型。
4.1 作动器传递阵模型优化
基于多目标遗传优化算法(NSGA-Ⅱ)建立针对图9中盆架状作动器的结构尺寸进行优化,设计空间为表1给出的初始尺寸的±10%,设优化目标:

表1 NSGA-Ⅱ算法参数设置

图9 作动器结构尺寸图
1) 作动器三相工作模态频率趋于一致。
2) 陶瓷片位于作动器最大应变处。
3) 驱动足振幅最大化。
算法参数设置如表1所示。算法迭代过程如图10所示。优化所得尺寸如表2所示。

表2 盆架状作动器优化尺寸
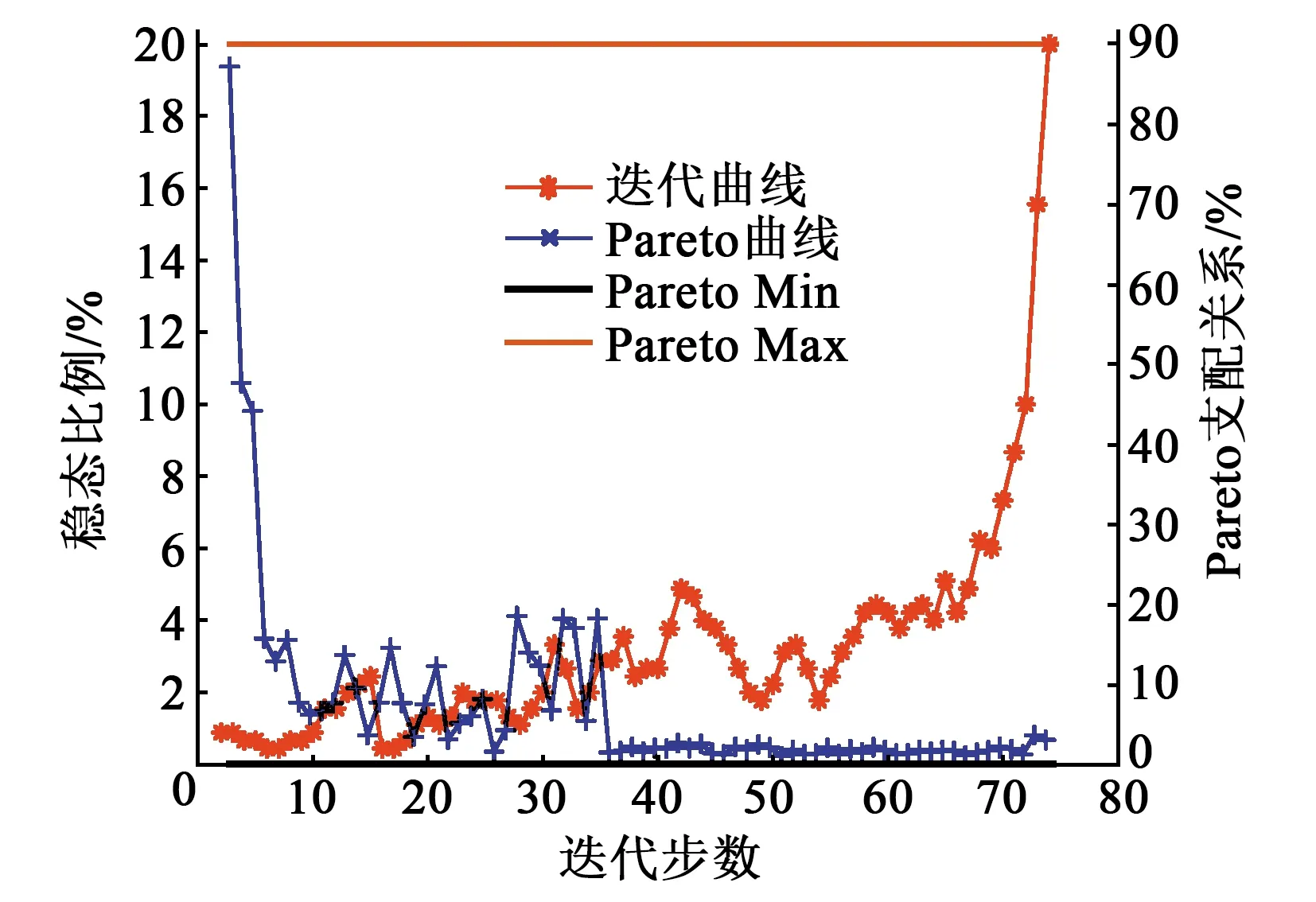
图10 目标函数迭代过程
由图10可知,优化算法迭代到第72步时满足优化终止条件,并输出表2的优化结果。为验证本次优化和所建立机电耦合模型正确性,选定45#钢为作动器基体材料,PZT-8为压电陶瓷材料,根据表2中优化后结构尺寸构造盆架状作动器有限元机电耦合分析模型,并进行作动器幅频特性分析和动力学特性分析对比分析实验。
4.2 作动器振型对比分析
振型是揭示压电作动器动态行为的重要属性之一。本节将通过对比传递阵法和有限元法(FEM)算得作动器前6阶振型,进一步验证传递阵模型的有效性。通过结合机械和电学边界条件,盆架状压电作动器驱动杆两端的速度分量可以根据传递阵模型来解决。因此,沿纵向划分的驱动杆部件中任何位置的剪切位移都可以用它们自己的传递阵Hi来计算。使用这种方法分别提取并绘制了由传递阵模型和有限元模型计算的相应振型,如图11所示。由图可看出,传递阵法的结果与有限元法的结果吻合较好,这充分证明本文所提传递阵模型适合于对盆架状压电作动器进行建模。
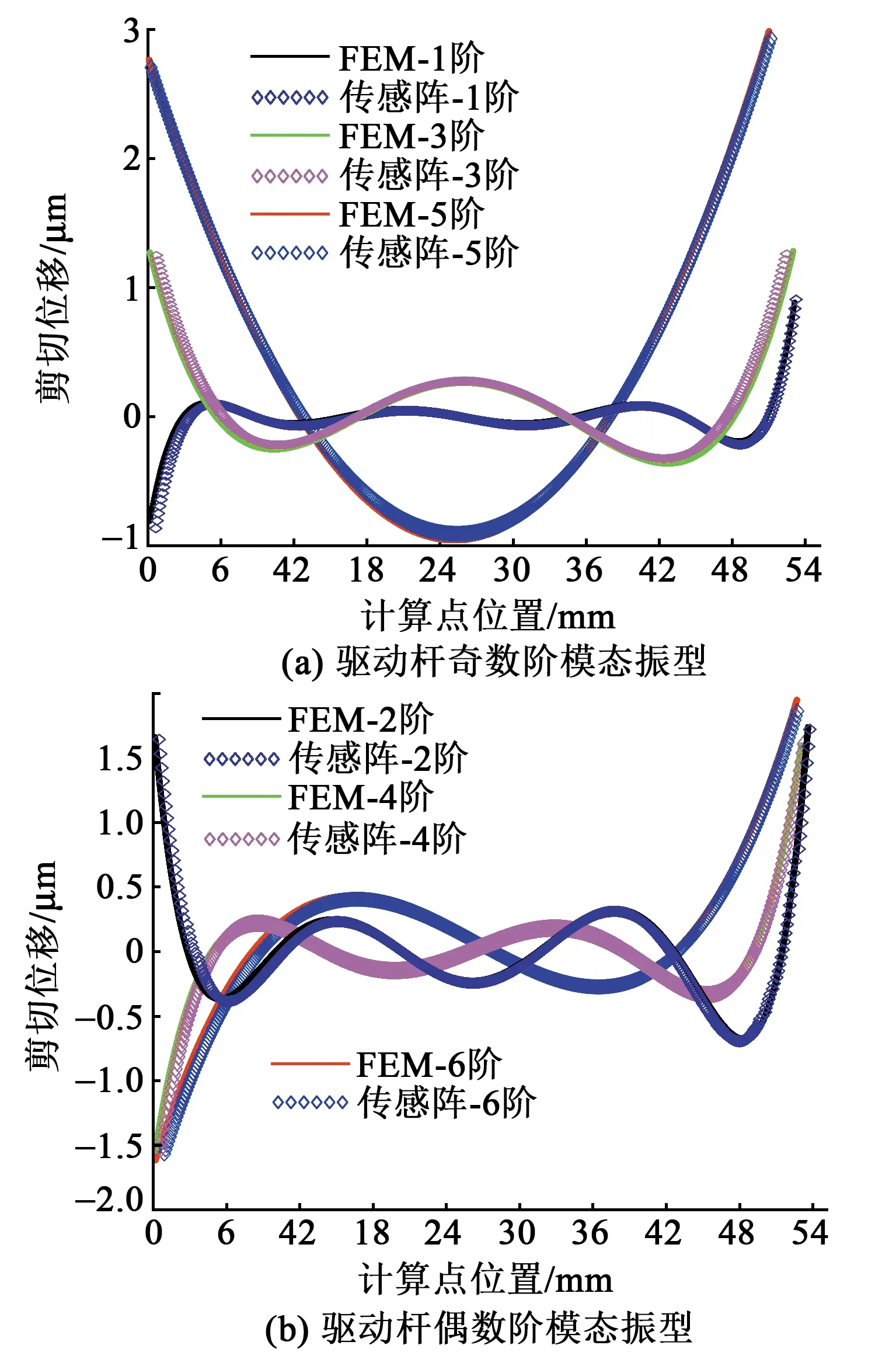
图11 盆架状作动器驱动杆前6阶弯曲振型对比
4.3 作动器幅频特性分析
为验证盆架状作动器机电耦合动力学模型的有效性,选取作动器1号驱动杆上驱动足进行幅-频特性分析。基于ANSYS谐响应分析模块,在压电陶瓷片表面施加250 V、基体接触面施加0的激励电压。设谐响应分析频域为43.0~45.5 kHz,计算步长为1 Hz/步,并提取计算结果。由图11可见,在频域为44.7~45.05 kHz时,三相工作模态均被成功激发,且三相工作模态频率分别为44 772 Hz、44 881 Hz和44 963 Hz,频率差为191 Hz,各相模态均在44 890 Hz左右出现峰值,且峰值附近区域无干扰模态,这说明作动器在此频段内工作稳定。针对作动器传递阵模型,采用与有限元仿真相同的电学激励条件,计算相同频率点上的幅值,得到相应的幅频特性曲线如图12所示。传递阵模型求得的三相工作模态频率分别为44 794 Hz、44 907 Hz和44 971 Hz,频率差为177 Hz。将该计算结果与数值仿真结果对比可知,二者对应工作模态频率差分别为22 Hz、26 Hz和8 Hz,传递阵法与有限元法结果存在偏差,可能是在对作动器进行传递阵建模时,对某些结构进行了简化处理导致的。对比两者计算结果证明了理论模型的有效性,可对作动器的共振频率进行较准确的预测。用于获得作动器频率响应特性的传递阵模型的计算时间仅几分钟。然而使用相同的计算机平台,从有限元计算出的相同结果需要4 h。因此,本文开发的传递阵模型的计算速度比有限元模拟的计算速度快。
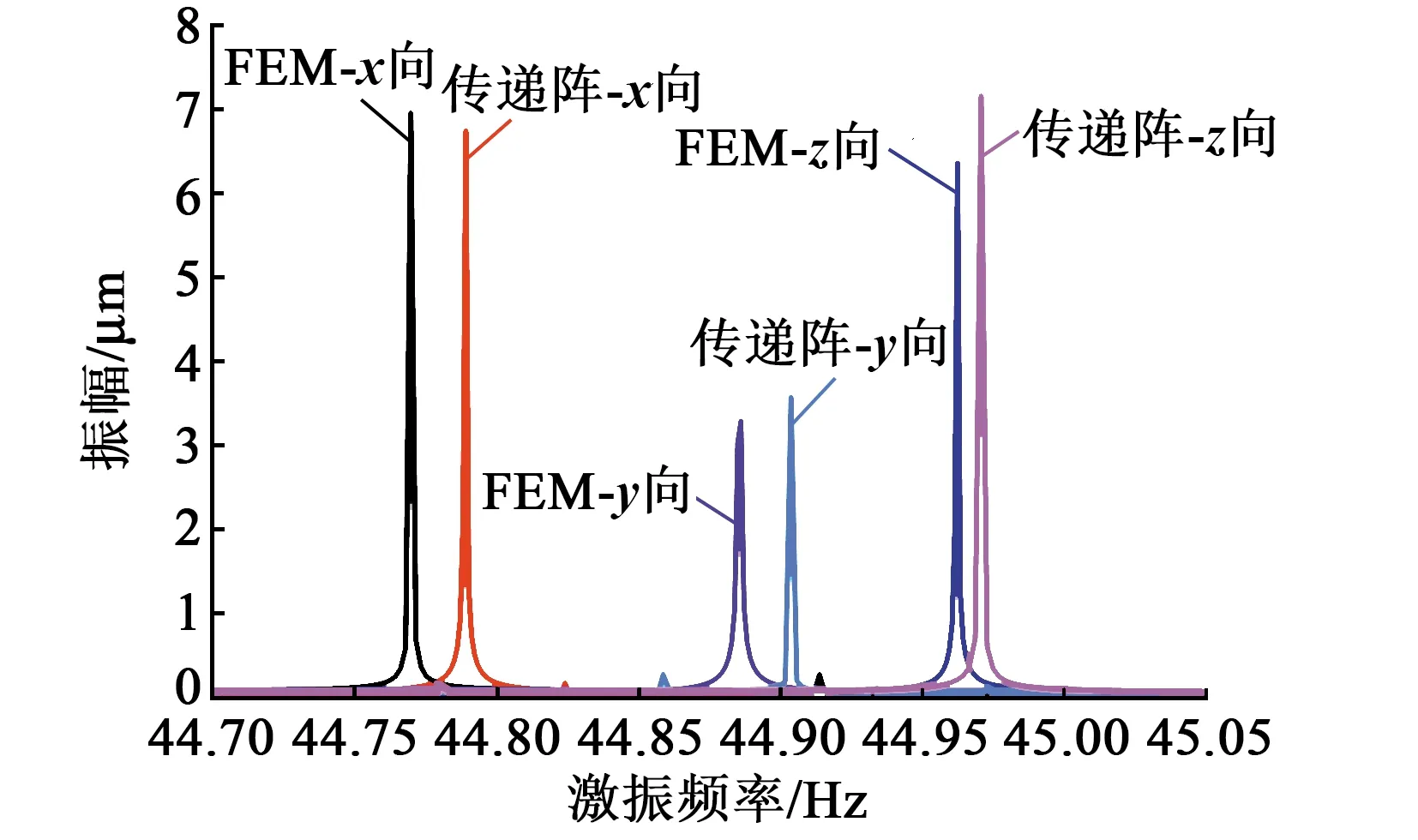
图12 FEM和传递阵法谐响应分析对比
4.4 动力学特性分析
为测试作动器驱动性能并进一步检验理论模型正确性,选取作动器1号驱动杆上驱动足质点,运用ANSYS瞬态响应求解器求解驱动足位移。
在作动器FEM模型的各陶瓷片上施加250 V、44 890 Hz的驱动电压,并设置瑞丽阻尼比ζ=0.02,且解算相应的α=5 639.07,β=7.09×10-8。为确保求得的位移响应曲线具连续性,采用完全法求解瞬态响应。提取到1号杆驱动足的响应如图13所示。由图可看出,驱动足进入稳态振动仅需1.2 ms,其x、y、z向振幅分别为2.95 μm、3.27 μm、1.37 μm,这三相振幅相近,从而有利于实现两杆交替驱动,并满足压电作动器运动要求。将同样大小的驱动电压施加在传递阵模型,所得结果如图13所示。图中,驱动足进入稳态振动时间为0.8 ms,x、y、z向振动幅值分别为3.12 μm、3.61 μm、1.82 μm。2个模型的结果基本吻合。这说明本文设计作动器半解析机电耦合动力学模型有效。
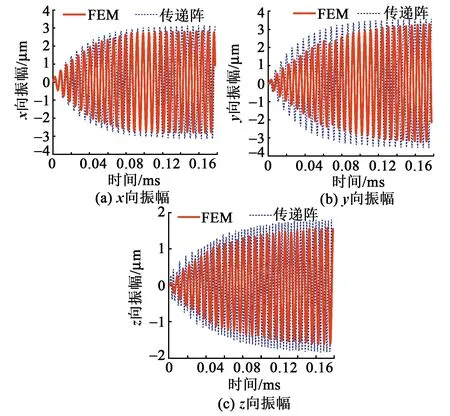
图13 驱动足的瞬态振动响应
5 结论
以状态向量为中间参量,借助结构传递阵力学原理并结合作动器边界连接条件,构建了盆架状作动器的理论模型,实现了其机电动力学特性的完整描述,可得结论:
1) 盆架状作动器在1 000 Hz频带内无干扰模态,其振动响应时间不超过1.2 ms,其驱动足沿x、y、z向振幅分别可达3.12 μm、3.61 μm和1.82 μm,该作动器具有良好的动力学输出特性。
2) 传递阵模型及有限元模型求得的盆架状平面作动器工作模态频率非常接近,故盆架状传递阵理论模型是有效的。
3) 采用传递阵法对压电作动器建模,可极大地降低压电平面作动器机电耦合动力学特性求解的时间复杂度。
4) 传递阵建模法特别适于以杆梁为主体的压电平面作动器的机电耦合动力学特性建模。
