带异形孔的双稳态压电能量采集器研究

周诗豪,宋 芳,熊玉仲

(1.上海工程技术大学 机械与汽车工程学院 上海 201620;2.上海工程技术大学 工程实训中心,上海 201620)

0 引言

随着能源的不断开发和利用,不可再生能源的有限性逐渐凸显。与常规能源不同,新能源是利用新技术开发利用环境中能源,再将新能源给能源传输系统提供电源[1-4],以满足微机械技术、嵌入式设备和无线传感器网络等低能量、低功率和独立工作系统发展的需要。新型能量收集技术已成为当前研究的热点之一。

微型压电振动能量采集器具有体积小,质量小,寿命长及无污染等优点[5-7]。传统压电振动能量采集器将压电陶瓷片通过导电胶贴合在振动悬臂梁结构上,从而发生应变产生电压[8]。这种采集方式在环境激振频率达到采集器整体的谐振频率时采集器的输出功率最大,一旦偏离该频率,输出的能量将急剧下降。因此,改善采集器的工作频带已成为研究者们关注的问题。

Vinod Rchalla等[9]提出了一种双向共振频率的可调谐振动能量收集装置,从低频环境中获取能量,进行了利用磁力技术的共振频率可调能量收集装置的设计和测试。刘颖等[10]设计了一种一、二阶悬臂梁低频压电能量采集器,使装置具有更低的工作频率及更宽的工作频带,与环境的低频更匹配。为了拓宽采集器的工作频带,杨斌强等[11]研究了一种带弹性放大器的双稳态能量收集器,装置与环境频率及固有频率不匹配时,仍可进行有效地收集能量。为了更进一步提高非线性能量采集器性能,赵泽翔等[12]研究了一种三稳态压电悬臂梁结构,利用磁荷法建立非线性磁力模型,与双稳态模型相比,三稳态的输出性能更高,且在理论方面也进行了优化。谭江平等[13]提出了一种四稳态的压电悬臂梁梁,研究表明,四稳态能量采集器可在低激励水平下工作,具有良好的工作频带和采集效率。熊玉仲等[14]设计了一种新型的压电悬臂梁能量收集器(PCEH),研究了频率、负载电阻和加速度对电压和功率的影响,其频率更低,输出电压和功率更高,提高了能量转换性能。通过使用Soildworks仿真研究发现,这种悬臂梁的谐振频率可通过改变金属板上孔的形状来进行优化,使悬臂梁的本征频率降得更低,从而与环境振动频率进行匹配。

针对此线性振动悬臂梁在偏离本征频率时输出功率密度快速下降的问题,本文设计了一种带异形孔的新型双稳态PCEH结构。在金属悬臂梁上开异形孔,减小了能量采集器的质量和体积,并采用磷青铜作为材料,降低PCEH的本征频率。与矩形孔悬臂梁模型相比,采用异形孔边缘的应力较大,悬臂梁获得的形变较大,输出能量产生也较大。利用多稳态的方法对这种新型双稳态结构进行了理论建模,建立了磁铁间的非线性磁力模型和采集器非线性耦合动力学方程。分析了采集器系统的势能和磁力变化趋势,对系统的动态特性进行数值分析,确定了采集器结构最佳实验参数,并制作样机进行试验对比分析和验证。

1 带异形孔的双稳态能量采集器的理论模型

1.1 几何模型

图1为带异形孔的双稳态压电振动能量采集器的结构模型。使用导电胶将压电陶瓷固定在金属悬臂梁上下两面。该结构中压电元件的发电方式采用d31模式。固定在悬臂梁上末端的磁铁A面向磁铁B的相极为N极,与磁铁B之间的磁作用力是排斥力,磁铁A、B的间距为d。

图1 带异形孔的双稳态压电振动能量

当系统受到激励时,悬臂梁作为主要振动结构,压电陶瓷片受到轴向应力发生形变,内部发生极化形成电压差。与无孔悬臂梁相比,异形孔悬臂梁提供的应力较大,频率较小。

图2为能量采集器简化结构的前视图。图中,定义悬臂梁的轴向为x轴,R(t)为外部激励,Z(t)为悬臂梁末端的位移,lf为压电陶瓷片长度,oa为宽度,h0为厚度,lg为磁铁和左侧机架的水平距离,lh为悬臂梁总长度,h1为厚度,磁铁A、B均为边长a的正方体。

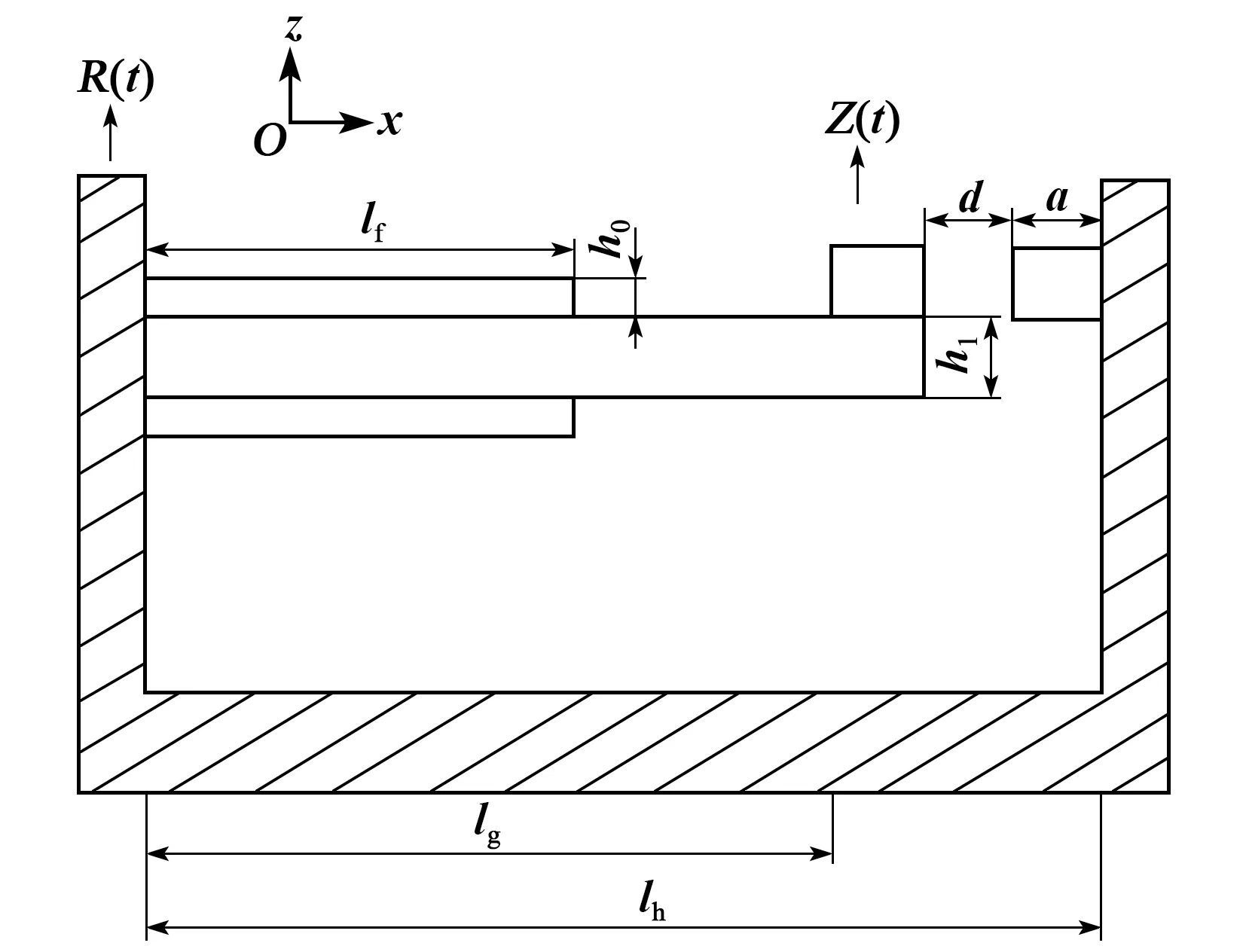
图2 非线性压电能量采集器的前视图

图3为带异形孔的金属悬臂梁结构图。悬臂梁宽度为oa,边缘圆弧半径为φa,异形孔的长度为lj。表1为能量采集器的尺寸和材料参数。

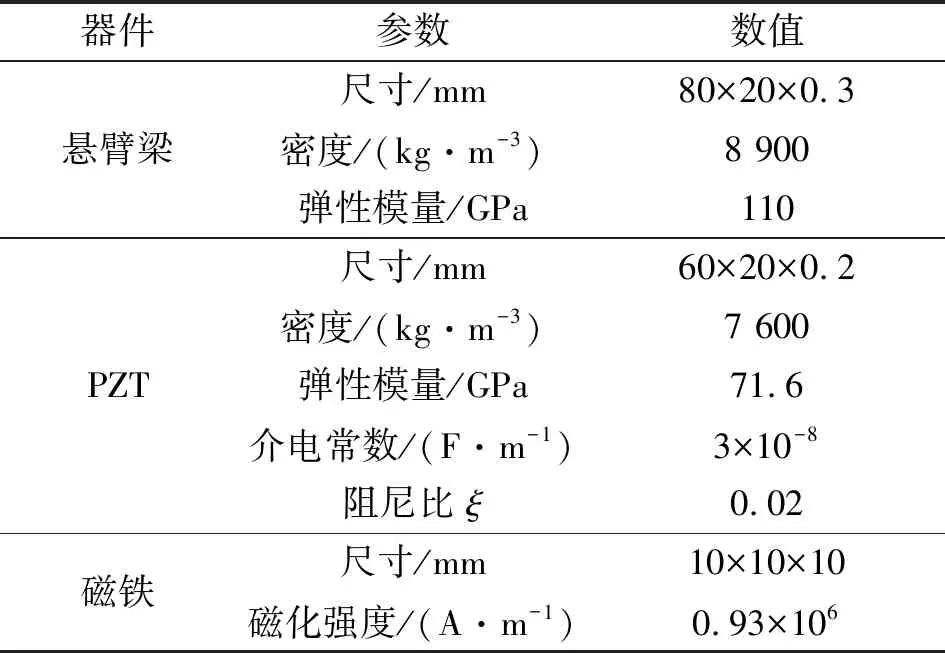
表1 能量采集器的材料和参数

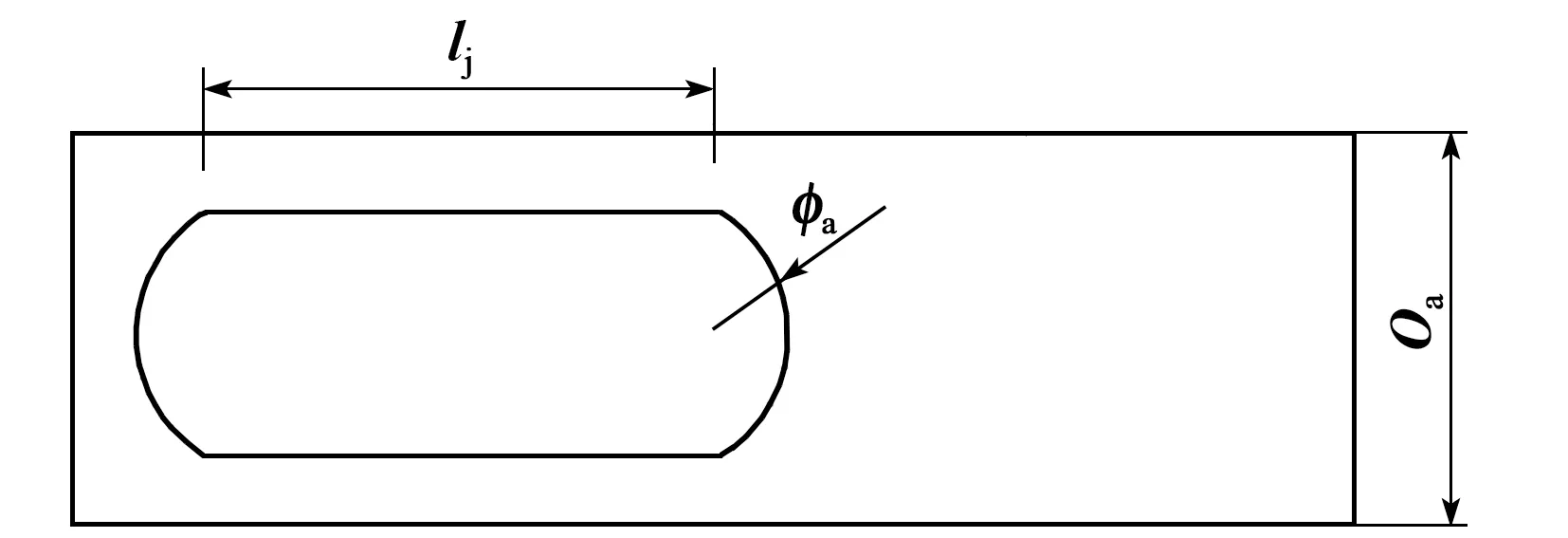
图3 带异形孔的金属悬臂梁

1.2 理论分析

由图2可看出,压电悬臂梁由上、下压电层和位于中间层的金属基板组成。系统的总等效刚度视为金属悬臂梁刚度和两片压电片刚度的叠加:

k=E1I1+2E2I2

(1)

式中:E1,E2分别为悬臂梁和压电陶瓷片的杨氏模量;I1为悬臂梁的截面惯性力矩;I2为压电陶瓷片的惯性力矩。其中:

(2)

(3)

由式(1)～(3)可得:

(4)

由于本能量采集器所期望收集环境的振动频率主要为低频,因此,振动时只取该结构的第一阶模态。压电悬臂梁总等效质量为

m=mA+ρc[(lg+a)·oa-ljφa-

(5)

式中:mA,mB分别为磁铁A、B的质量;ρc,ρp分别为金属悬臂梁和压电陶瓷片的密度。

系统的等效阻尼为

(6)

式中ξ为系统阻尼比。

假设悬臂梁是欧拉-伯努利梁,且假设压电片和悬臂梁之间的粘结是理想的,悬臂梁在z轴方向做弯曲运动,根据基尔霍夫定律和牛顿第二定律,对整个系统进行分析可知,系统的等效电路模型方程:

(7)

式中:V(t)为输出电压;δ为压电陶瓷片机电耦合系数;Fv为磁铁之间竖直方向分力;Cq为压电陶瓷片静态电容;Rs为负载。

为了简化后续能力采集器的磁力势能计算步骤,假设磁场在磁体内部均匀分布,将每个磁铁看成是一个点磁荷,利用磁偶极子模型原理建立非线性磁力模型。

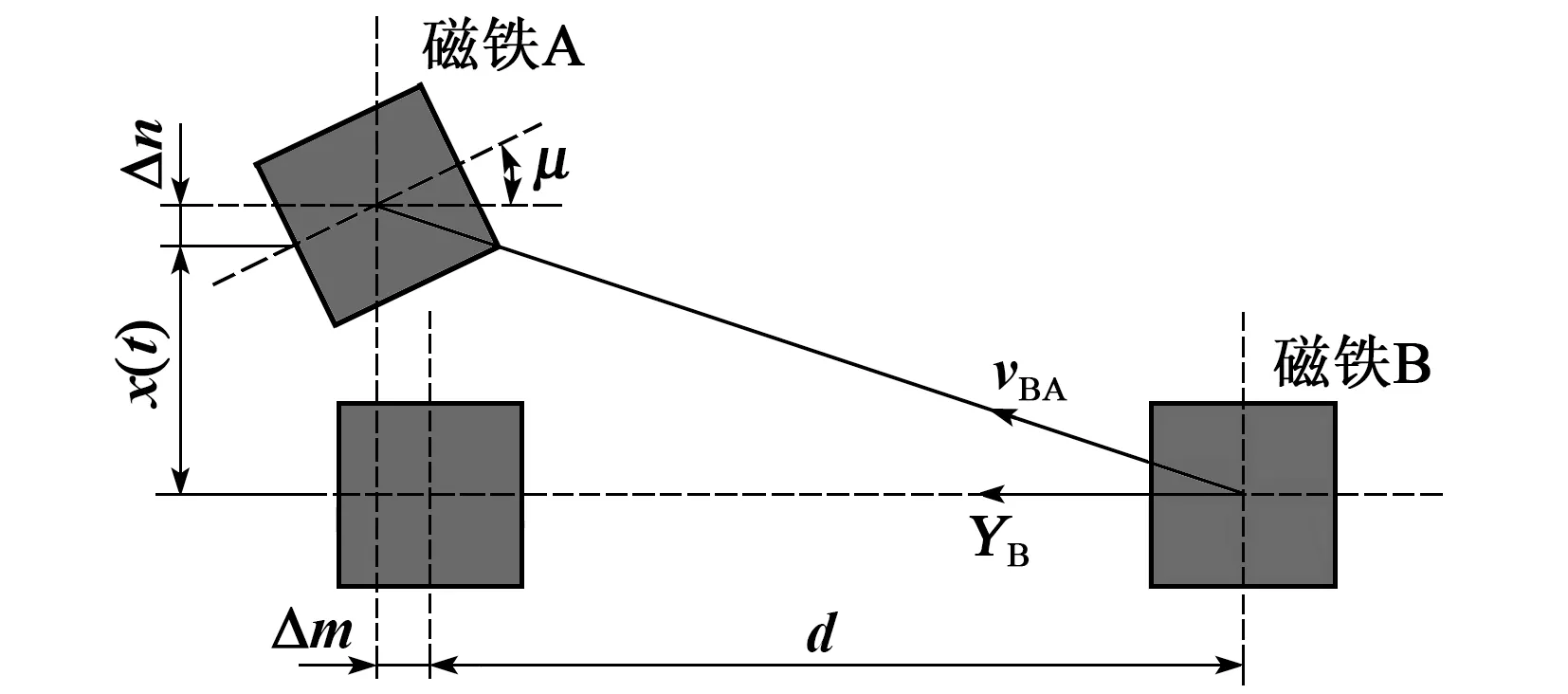
图4 磁体间的非线性磁力模型

qA=(icosμ+jsinμ)BAVA

(8)

qB=iBBVB

(9)

式中BA、BB分别为磁铁A、B的磁化强度和;VA、VB分别为磁铁A、B的体积。

磁铁B到磁铁A的方向向量为

vBA=-id+jZ(t)

(10)

磁铁间的势能为

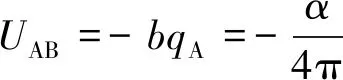
(11)

式中:b为磁铁B在磁铁A处的磁通密度;α为真空磁导率;∇为向量梯度算子。

将式(8)～(10)代入式(11)可得:

(12)

根据式(11)对位移求导可得磁铁A、B间的垂直磁力:

(13)

将式(12)代入式(13)可得:

(14)

由式(12)、(14)可知系统的总势能为

(15)

2 实验分析

图5为实验平台。测试时,将能量采集器固定在激振器上,由信号发生器产生一定频率的正弦波信号经功率放大器放大以驱动激振器,从而产生初始激励,能量采集器受到激励工作,将电信号输入示波器进行记录。

图5 实验平台

对能量采集器的势函数进行数值分析后得出双稳态能量采集器的分叉点在12 mm附近,故设置实验测试磁间距4 mm、8 mm、12 mm、16 mm、20 mm共5组进行实验。信号发生器产生正弦波形,设置激振频率为10～30 Hz,步长为0.5 Hz。

如图6所示,当磁极对间距为4 mm、8 mm时,磁极对间的磁作用力太大,带异形孔结构的双稳态能量采集器工作时不能越过势能阱,所以输出电压较低。当磁极对间距为12 mm,能量采集器工作时可越过势能阱在谐振频率附近大幅摆动,输出电压最大。继续增大磁间距,磁极对间的作用力减小,双稳态效应减弱,在谐振频率附近摆动幅度也减小,输出电压降低。

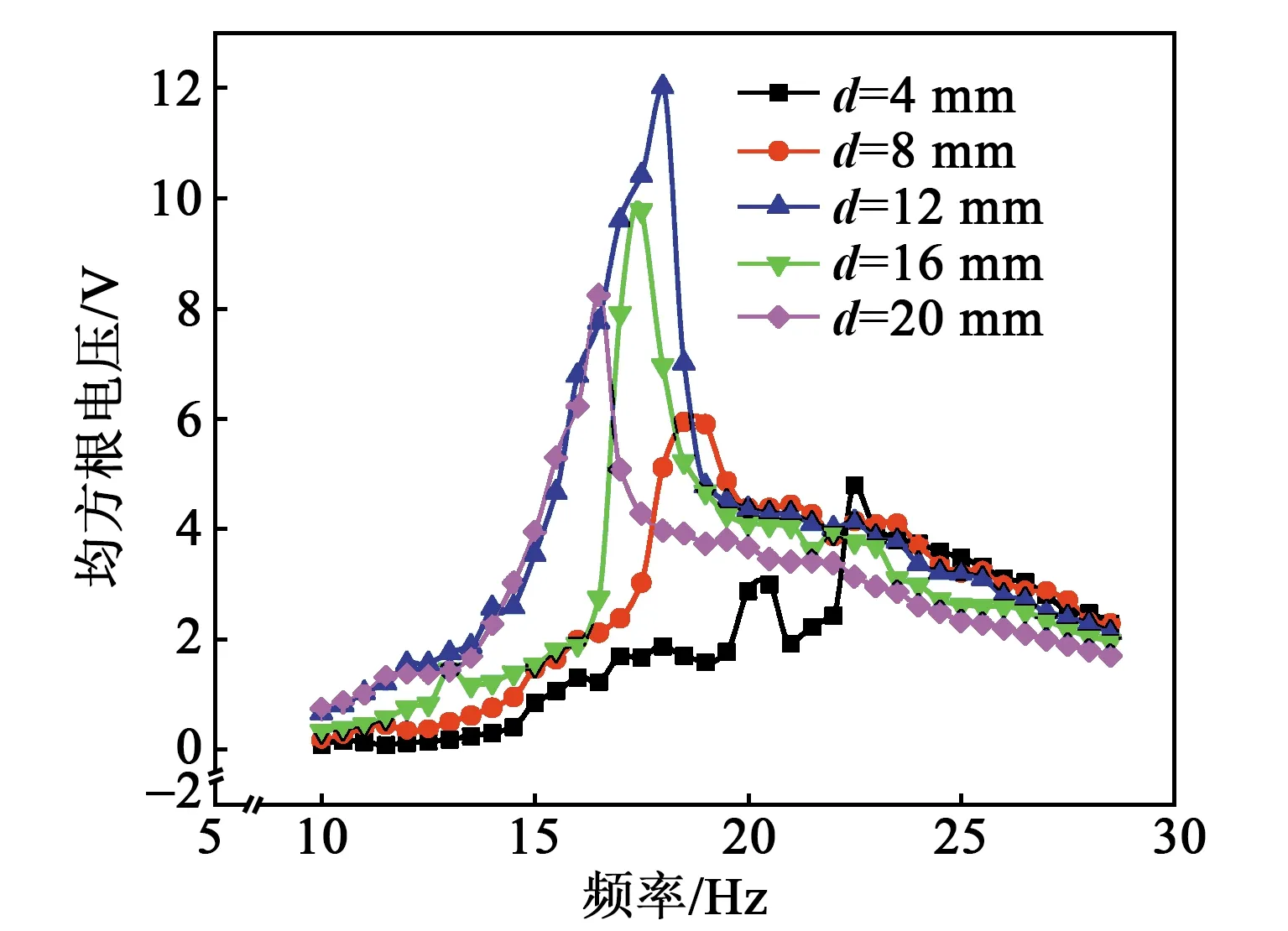
图6 带异形孔结构的双稳态能量采集器在不同磁间距下的频率-电压曲线

通过实验可知,带异形孔结构的双稳态能量采集器,磁极对间距为12～20 mm工作时,系统处于双稳态模式,且有足够能量越过势阱,能量采集器振动较大。当磁极对间距为12 mm时,在15.5～22.5 Hz内均有较大的均方根电压输出,为期望的工作频率区间。表2为带异形孔结构的双稳态能量采集器在不同间距下的性能参数表。

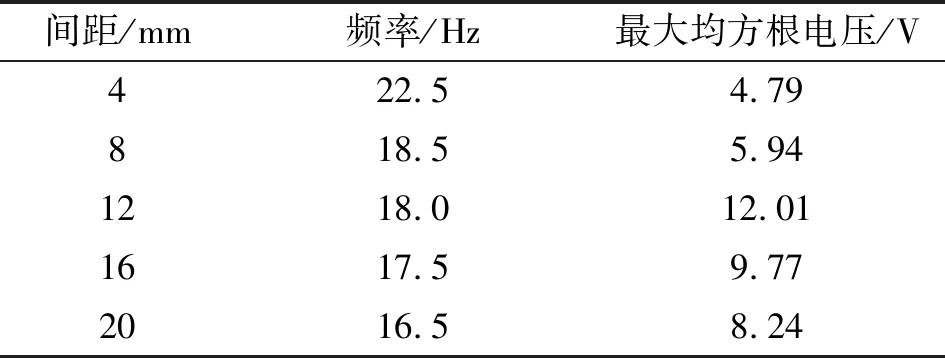
表2 带异形孔结构的双稳态能量采集器在不同间距下的性能参数表

如图7所示,带异形孔结构的双稳态能量采集器在不同磁极对间距下输出的最大均方根电压为12.01 V,谐振频率为18 Hz。传统结构的双稳态能量采集器和带方形孔结构的双稳态能量采集器在不同磁极对间距下输出的最大均方根电压分别为10.25 V和9.37 V,此时谐振频率分别为19 Hz和20 Hz。带异形孔结构的能量采集器在激振频率为18 Hz时达到谐振状态,可在更低频率范围实现双稳态效应。带异形孔结构的双稳态能量采集器的均方根峰值电压相较于传统的双稳态能量采集器和带方形孔的双稳态能量采集器分别提高了28%和17%,以4 V为标准电压工作阈值,其工作频带分别拓宽了5.5 Hz和4.5 Hz。

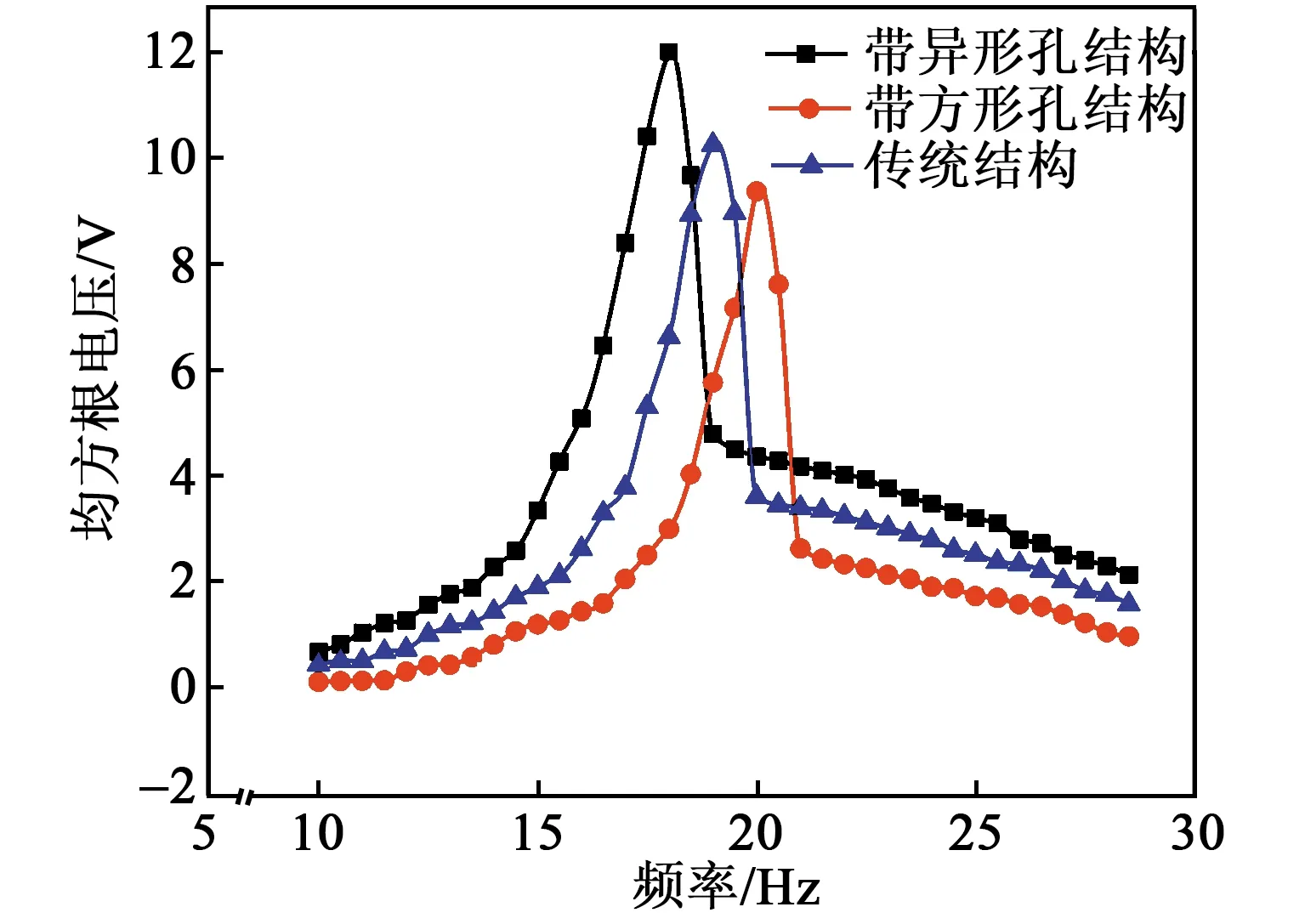
图7 不同孔结构的双稳态能量采集器的频率-电压曲线

3 结论

为了提高对环境中低频能量采集效率,本文提出了一种金属基板上带异形孔结构的双稳态压电振动能量采集器,在较低工作频率下仍保证了可越过势阱的双稳态工作模式。建立了采集器模型,分析了新结构的力学模型,推导计算出了带异形孔结构的双稳态能量采集器的系统总势能表达式,对这种新型的双稳态能量采集器与传统双稳态能量采集器和带方形孔结构的双稳态能量采集器进行了对比实验分析。主要结论如下:

1) 随着磁间距的减小,带异形孔结构的双稳态能量采集器的双稳态效应先增强再减弱。

2) 相比传统的双稳态能量采集器和带方形孔的双稳态能量采集器,带异形孔的双稳态能量采集器在一定电压阈值下工作的频带更宽,可采集的振动频段更低,输出效率更高。