多悬臂梁振动能量收集器的仿真与试验

孙黎阳,滕 燕,徐 迎

(南京理工大学 机械工程学院,江苏 南京 210094)

0 引言

工业自动化生产中[1],在排气阶段时,气动系统大量能量随着压缩气体直接排出大气而被浪费[2]。为降低气动系统能量损耗,Yang A等[3]将传统气缸通过旁通阀连接,减少超调和重复利用压缩空气,从而减少了气缸中约28%的能源消耗。Li T C等[4]在气缸排气口外接增压储气罐,通过储气罐可回收40%的排出气体,但试验表明,这种直接回收排出气体能量的方式将产生背压,因而影响气动系统正常工作。压电薄膜已被广泛应用于能量收集系统中,通过外加激励使薄膜振动,产生数十微瓦甚至毫瓦级的电量[5]。Ding L等[6]设计了一种鳍形扰流柱,使其在低速风场中带动悬臂梁振动,悬臂梁上的PZT压电片也进行受迫振动产生电荷。试验表明,该种能量收集器峰值电压可达18.1 V,最高功率为1.645 mW。白凤仙等[7]设计了一种非接触式聚偏二氟乙烯(PVDF)三角形压电梁,利用拥磁梁所受风能的激励带动三角形压电梁振动,从而实现对风能的收集。试验结果表明,在风速为2.80～5.25 m/s时,该种能量收集器系统的平均功率为13.6 μW,峰值电压为13.4 V。研究证明了压电片在低速流场中俘获能量的便捷性,但由于气缸排出气体属于高压压缩气体,其流速远大于风速。因此,应用于低速流体中的能量收集器在压缩气体中的适用性将受限。基于收集风能的能量收集器的启发和影响,陈至杰[8]设计了一款适用于回收压缩气体的C型绕流块气动系统能量收集器,试验表明,该装置接入气动系统,在不影响气动系统正常工作时,在压缩气体的作用下PVDF压电片发生振动,使能量收集器最大功率可达93.7 μW。但该设计对压缩气体排出时呈现射流状的特点未充分利用,因此还存在很大改进空间。本文基于该收集器的工作原理,充分分析了射流流体流场的特点,设计了一款多悬臂梁振动的能量收集器,通过改变压电片的放置方式和增加压电片的数量,从仿真和试验的角度证明了该能量收集器可提高压电片总输出功率。

1 能量收集器结构设计

压缩气体通入能量回收装置时,其流场呈射流状。经过一段距离的扩散,流场范围将远大于进口直径。若用3片压电片对流场能量进行收集,则其对流场的利用率远大于单片压电片对流场的利用率。由于压缩气体冲击扰流柱时会产生很大的力,为避免压电片被压溃,将扰流柱固定于压电片前方,使压电片在扰流柱后,受卡门涡街效应后进行受迫振动产生电荷,其工作示意图如图1所示。

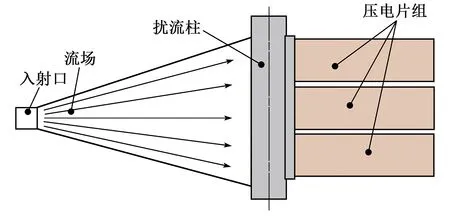
图1 压电片工作示意图

为充分利用射流场的流动特点,设计的多悬臂振动能量收集器组件如图2所示。压缩气体从入射口通入能量收集器中形成射流,经过一段距离的扩散,压缩气体冲击扰流柱,并在扰流柱后方产生卡门涡街现象。扰流柱通过支撑装置及连接装置与外壳相连,并固定于试验台上。扰流柱后方放置PVDF压电片,压电片受卡门涡街现象的影响后进行受迫振动产生电荷,通过外接回收电路对该能量进行收集。

图2 能量收集器结构示意图

2 能量收集器流场仿真计算

2.1 控制方程

为了分析压缩气体在能量收集器中的流场情况,本文对相应的试验进行了仿真计算。取能量收集器的A-A面(见图3)为分析面,对扰流柱后涡脱频率进行分析,取能量回收器中整体流体和压电片为分析对象,对压电片振动进行流固双向耦合分析。假定压缩气体是二维非定常流动,由于能量收集器入口流速大于0.3马赫(1马赫=1 224 km/h),因此设定压缩气体可压缩。采用非定常雷诺平均Navier-Stokes方程(N-S方程),并结合适用于高雷诺数湍流模型的k-εRNG湍流模型求解流场[9-10],其控制方程为

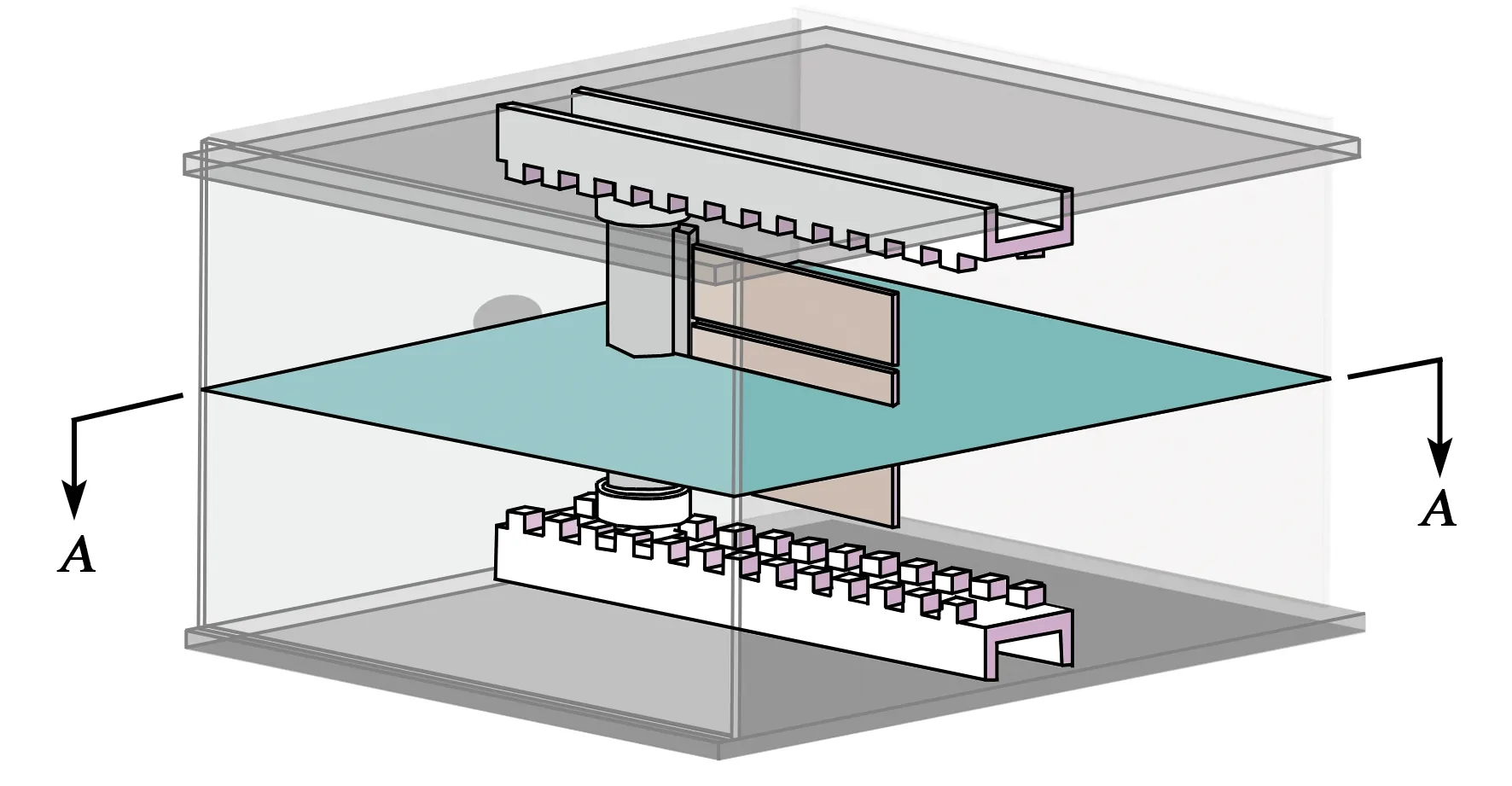
图3 仿真计算面示意图

(1)

(2)

仿真基于Ansys Workbench平台,采用Fluent有限体积法进行瞬态数值计算。动量方程和连续性方程均采用基于压力的耦合求解。

对PVDF压电片振动进行分析时,由于PVDF压电片均固定于扰流柱后进行受迫振动。因此本文将PVDF压电片振动系统简化为质量-弹簧-阻尼模型,如图4所示。根据欧拉-伯努利梁的假设[11],忽略PVDF压电片在振动中的剪切变形和惯性矩,视其为单自由度振动。各压电片由经过扰流柱产生的升力与阻力的综合作用下进行受迫振动。PVDF压电片的运动方程可简化为

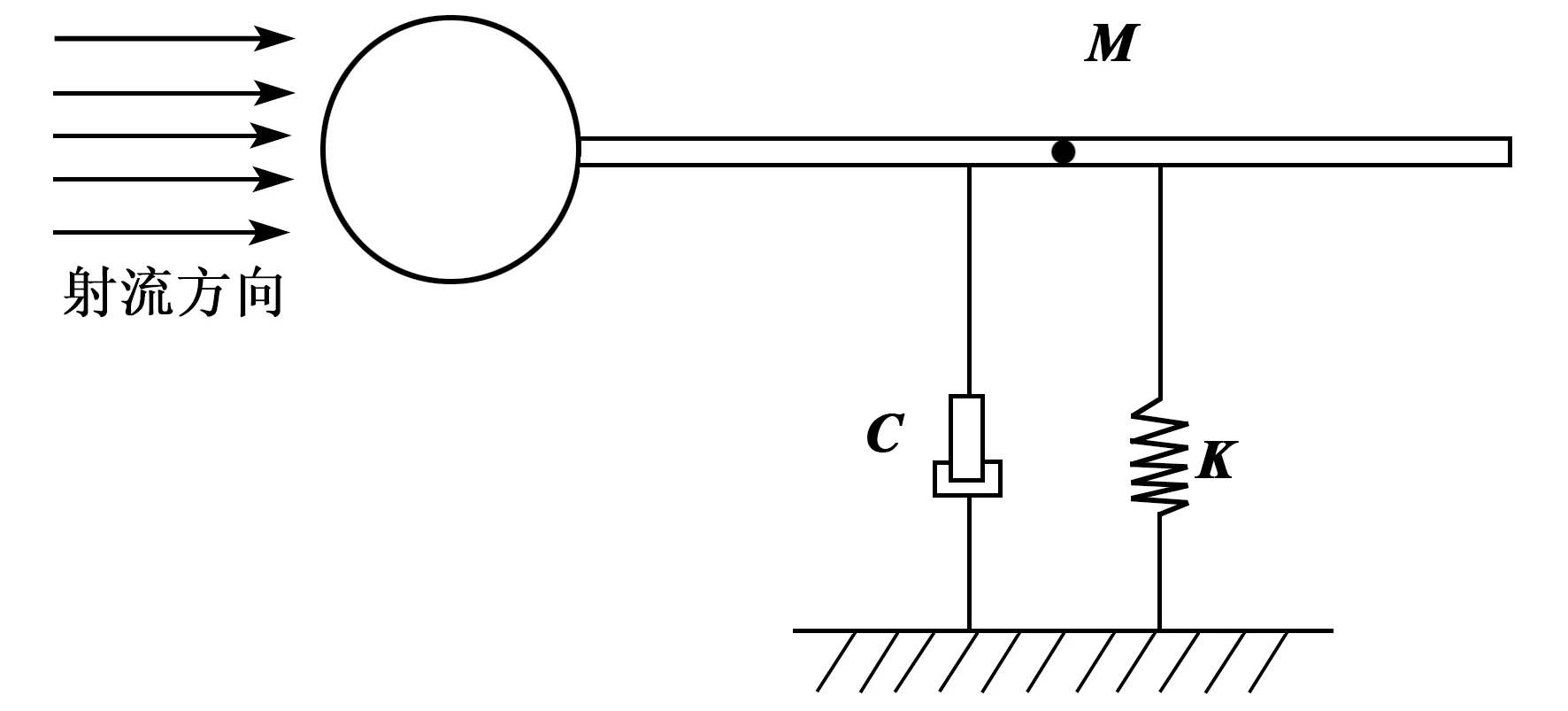
图4 单个振动模型示意图

(3)

式中:M为系统的等效质量矩阵;C为系统的等效阻尼矩阵;K为系统的等效刚度矩阵;y为PVDF压电片沿Y轴的位移;Ffluid为等效合力矩阵。

本文PVDF压电片结构和尺寸示意图如图5所示。其中,l、w、h分别为PVDF薄膜和共聚体的长、宽、高。压电片的物理参数如表1所示。受迫振动时边界条件为电学短路和机械加持。因此由压电本构方程可得压电片应变S、电场强度E与电位移D的方程为

表1 PVDF压电片物理参数

图5 PVDF压电片结构和尺寸示意图

(4)

2.2 仿真计算

由于压电片产生电压的大小与其振动相关,因此本文首先对压电片模态和所处流场的振动频率进行仿真分析,使压电片在振动时尽量处于共振状态,并产生更高的电压。

本文选用智美康科技(深圳)有限公司生产的PVDF压电片,其物理参数如表1所示。固定压电片的一端,仿真得出其1～6阶的模态如表2所示。

表2 PVDF压电片模态

压电片所处流体的振动频率即为圆柱绕流的涡脱频率,该流体场的计算域和网格划分如图6所示。图中,D1为压缩气体入射口直径,d=40 mm为压缩气体管口与扰流柱的距离,D2为扰流柱直径。入射口边界条件为50 kPa均匀压力分布,出口边界压力为0。

图6 流体场计算域和网格示意图

在D1=∅6 mm、∅8 mm、∅10 mm、∅12 mm,D2=∅6 mm、∅8 mm、∅10 mm、∅12 mm时,分别监测扰流柱的升力系数,再根据升力系数得出其对应的功率谱密度。其对应的功率谱密度频率范围即为扰流柱的涡脱频率范围。取涡脱频率范围中位数为对应涡脱频率,结果如图7所示。

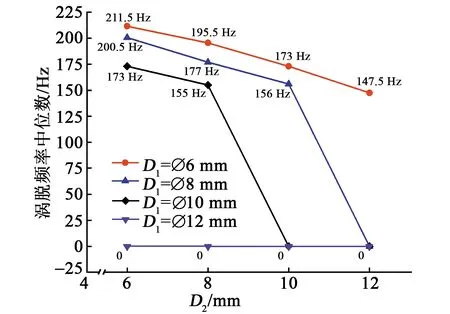
图7 流场涡脱频率变化图

由图7可看出,随着D1和D2的增加,扰流柱后方涡脱频率逐渐下降。当D1和D2变化时,涡脱落频率为147.5～211.5 Hz。且当D1=∅8 mm、D2=∅12 mm;D1=∅10 mm、D2>10 mm;D1=∅12 mm时,扰流柱后方将不能形成涡脱落现象。正常涡脱落效果和无涡脱落效果如图8所示。

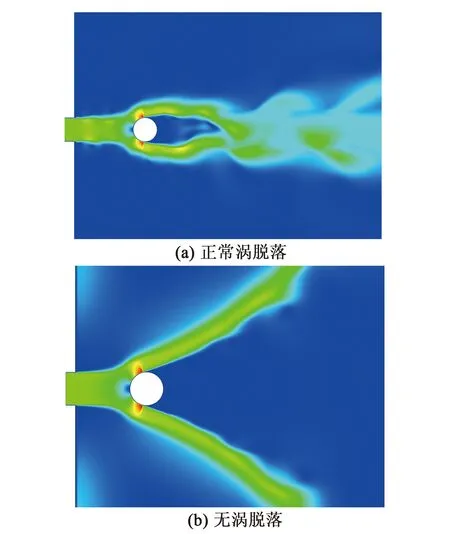
图8 两种涡脱落效果示意图

由文献[12]可知,当PVDF压电片处于机械夹持状态时,其产生的电压与压电片振幅和频率呈正相关。若将压电片置于上述流场,则可知该流体场对压电片的激励频率与压电片二阶模态振动频率接近,当两者越接近时,压电片越易产生共振[13-15]。因此,结合PVDF压电片模态频率与仿真所得流场涡脱落频率,选定D1=∅8 mm,D2=∅8 mm,对能量收集器进行单悬臂梁和多悬臂梁振动的流固双向耦合仿真。

流固双向耦合采用上述所用湍流模型,流体域中与压电片接触的面设为动网格耦合面,固体域压电片各个面设为耦合面,压电片在入射口压力为50 kPa时,单悬臂、多悬臂梁中1～3号悬臂梁的压电片振动情况如图9所示。

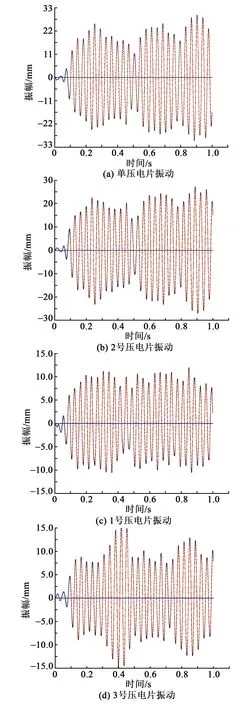
图9 各压电片振动示意图

由图9可看出,单悬臂梁压电片与多悬臂梁2号压电片的振动图形几乎一致,因此,多悬臂梁加入的1、3号压电片未影响2号压电片的振动。而1、3号压电片的振动又证明了该结构的能量收集器充分利用了射流场的特点,能够提高能量收集器的效率。由于流固双向耦合计算量过大,关于入射口压力,扰流柱距入射口距离等参数如何影响压电片实际生电的研究,本文将使用试验的方式进行研究。

3 能量收集器试验研究与分析

为获得压电片实际产生的电压数据,根据气动测试回路(见图10)搭建了试验平台,其中能量收集器各连接部件采用3D打印进行制造。试验时,压缩气体经过减压阀和压力传感器后冲击扰流柱,使压电片产生振动。电荷由标准能量收集(SEH)电路完成收集,通过虚拟示波器和计算机得到压电片开路电压和SEH电路中电阻的负载电压。

图10 试验装置气动测试回路

结合仿真结果(见图7)选用d=40 mm,排出气体压强为50 kPa,D1、D2分别在∅(6～12)mm变化时,测量2号压电片在开路条件下产生的电压,结果如图11所示。

图11 电压随D1、D2变化图

由图11可看出,当D1=∅8 mm,D2=∅8 mm时,2号压电片产生的电压最大(为10.70 V),而这与仿真试验(见表2和图7)中该试验组涡脱落频率最接近压电片二阶模态相对应,说明了仿真的可靠性。对于仿真结果(见图7)中正常涡脱落的试验组,2号压电片电压为8～11 V,而对于无涡脱落效果的试验组,2号压电片电压为5～7.5 V,且D1和D2对压电片产生电压的影响表现出交互作用。因此,选择D1=∅8 mm,D2=∅8 mm进行后续试验。

结合仿真结果(见图7)选用D1=∅8 mm,D2=∅8 mm,d=40 mm,排出气体压强为10～80 kPa时, 测量PVDF压电片在开路条件下产生的电压,结果如图12所示。由图可看出,随着压强的增大,各PVDF压电片产生的电压均逐渐上升。在80 kPa时电压达到最大,其中,1号压电片电压为9.27 V,2号压电片电压为16.41 V,3号压电片电压为9.49 V,单悬臂梁压电片电压为16.22 V。由电压变化趋势可得出,随着排出气体压强的增高,PVDF压电薄膜产生的电压会持续升高,且多悬臂梁能量收集器的2号压电片振动生电效果与单悬臂梁压电片振动生电效果一致,这也验证了仿真结果的可靠性。

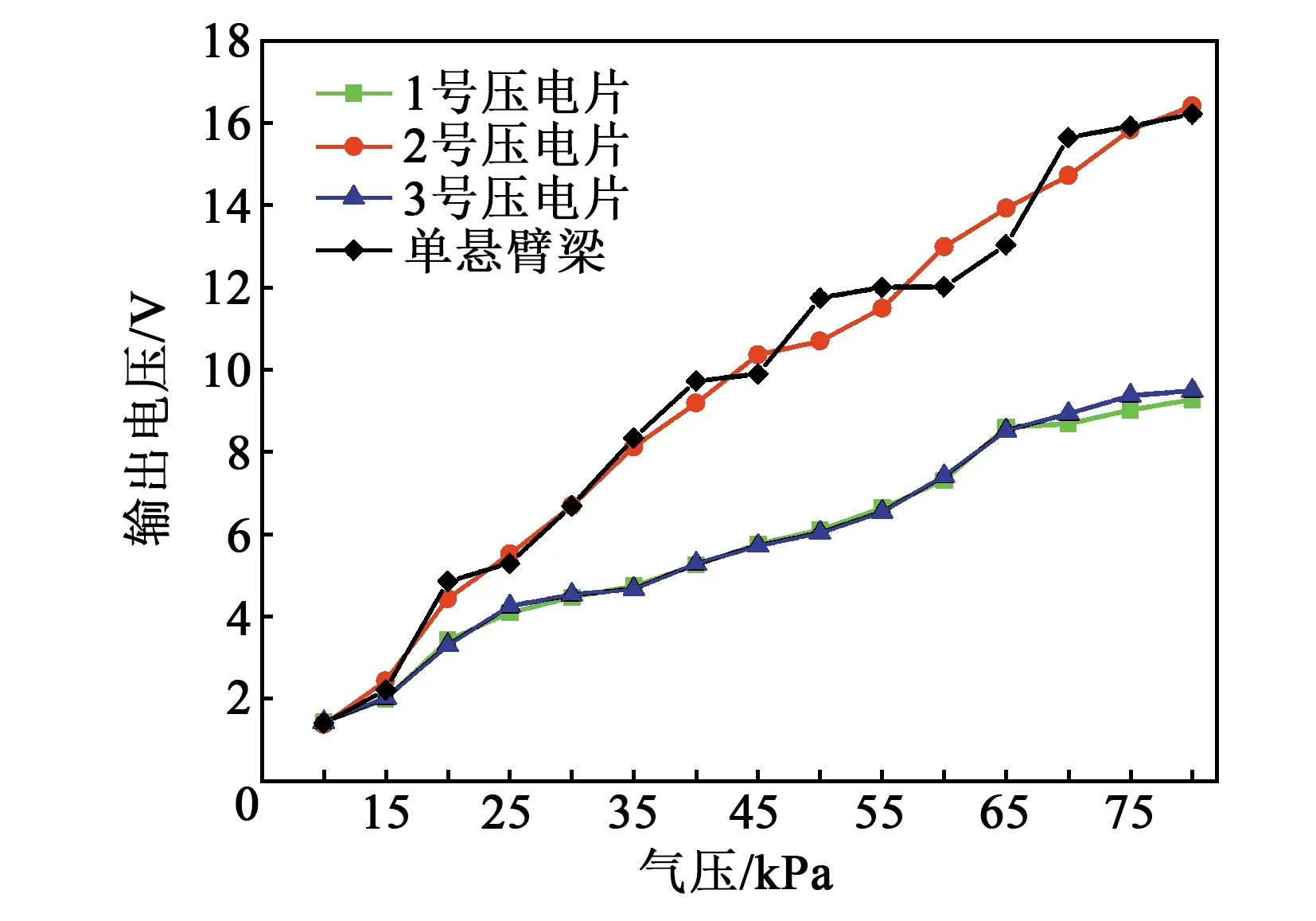
图12 电压随气压变化图

结合仿真结果(见图7)选用D1=∅8 mm,D2=∅8 mm,排出气体压强为50 kPa,测量d=10～100 mm时,PVDF压电片在开路条件下产生的电压,结果如图13所示。由图可看出,在d=70 mm处,1、3号压电片产生最大电压,分别为9.68 V和9.74 V。在d=90 mm处,2号压电片和单悬臂梁压电片产生最大电压,分别为16.57 V和16.12 V。由电压变化趋势可得出,处于中间位置的2号压电片距离扰流柱的最佳发电位置,比1、3号压电片距离扰流柱的最佳发电位置远;且1、3号压电片产生电压时,不会影响2号压电片振动产生电压。

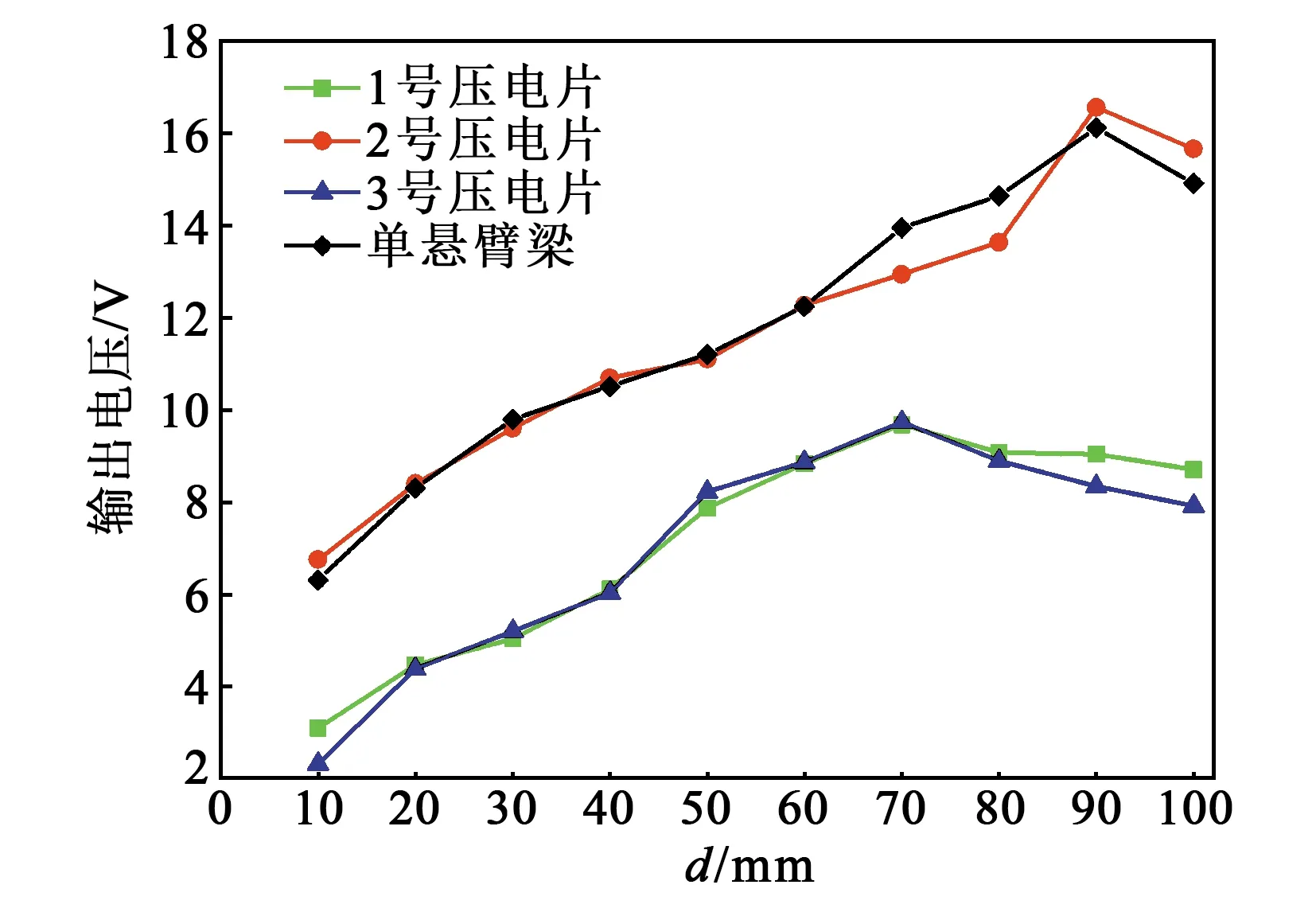
图13 电压随d变化图

选用D1=∅8 mm,D2=∅8 mm,d=80 mm,将1～3号压电片分别外接SEH电路,负载电阻为100～1 000 kΩ,排出气体压强为10～80 kPa时,测量其电阻两端的最大电压对应的负载功率,结果如图14所示。由图可看出,1号压电片在排出气体压强为80 kPa,负载电阻为900 kΩ时,功率达到最大(为23.26 μW);2号压电片在排出气体压强为80 kPa,负载电阻为900 kΩ时,功率达到最大(为73.85 μW);3号压电片在排出气体压强为80 kPa,负载电阻900 kΩ时,功率达到最大(为23.52 μW)。3组压电片总功率最大可达120.64 μW。

图14 功率随电阻和气压变化示意图

4 结论

本文通过仿真和试验分析了不同入射口直径、扰流柱直径、排气压力、扰流柱距入射口距离对压电片效果的影响,以及不同负载电阻和入射口压力对能量收集器能量回收功率的影响,结果表明:

1) 入射口与扰流柱直径对压电片振动有交互作用,增加入射口直径和扰流柱直径能够降低压电片的振动频率。但过大的入射口直径和扰流柱直径会导致涡脱落现象消失。

2) 随着入射口压力的增加,压电片产生的电压也逐渐增加,且压电片的电压与入射口压力成正比。

3) 本文所设计的各压电片不会对各自工作产生干扰。2号压电片对入射口的最佳工作距离是90 mm,1、3号压电片对入射口的最佳工作距离为70 mm。

4) 本文设计的多悬臂梁能量收集器最大总功率可达120.64 μW,与现有气动系统单悬臂梁能量回收装置[8]相比,其最大功率提高了28.8%。