基于复合控制的压电驱动器设计方法
2023-05-31许泽宇张寒冰崔永浩
王 哲,张 望,许泽宇,张寒冰,崔永浩
(北京无线电测量研究所, 北京 100854)
0 引言
压电陶瓷作为一种常见的微动位移智能材料,具有响应速度快,分辨率高,体积小及能量密度大的优点,现已成为光学、电子学相关的精密定位研究领域中的重点研究对象[1-2]。目前广泛应用于扫描探针显微镜、半导体加工、高精度机床及激光设备中,但其自身存在的蠕变、迟滞等非线性因素对定位精度带来了较大的误差[3],虽然采用闭环控制方式能显著提升其稳态精度,但动态精度难以保证。为此,研究者们期望通过建立压电陶瓷的前馈逆模型来对压电陶瓷的非线性误差进行补偿[4]。目前,典型的现象学迟滞模型包括Duhem模型[5-6]、Bouc-Wen模型[7]、Preisach模型[8]、Krasnoselskii-Pokrovskii(KP)模型[9]及Prandtl-Ishlinskii(PI)模型[10-12]等。Duhem模型和Bouc-Wen模型均是通过微分方程来描述压电迟滞现象,微分形式下的非线性表达式使模型的参数识别较难。Preisach模型是基于算子的迟滞模型,有积分表示和解析不可逆问题。作为Preisach模型的子类,经典PI模型通过一个阈值变量和一个密度函数来描述滞后现象,可看作是简单迟滞算子的叠加,降低了建模的复杂性,实现了解析的可逆性,但其无法描述复杂的不对称迟滞曲线。KP模型能够描述不对称迟滞现象和饱和迟滞效应,然而为KP模型构造逆模型是一个很大的挑战。广义PI模型保留了经典PI模型的建模简单及逆模型可解析的优势,同时通过增加包络函数描述复杂的迟滞曲线[13]。
为了便于系统集成及小型化,采用数字信号处理(DSP)结合现场可编程门阵列(FPGA)(DSP+FPGA)数字控制芯片作为压电驱动器的嵌入式控制系统。将广义PI模型的参数在DSP中在线辨识,实时更新系统模型,并通过逆模型公式计算前馈补偿分量,将前馈补偿结果通过数据总线发送给FPGA。压电驱动系统闭环在FPGA中实现,采用比例积分控制结合前馈补偿的复合控制,并在FPGA中实现高速高精度模数(A/D)采样及数模(D/A)输出。最终实现系统控制频率为50 kHz,求得跟踪频率分别为50 Hz、100 Hz、200 Hz对应的动态均方根分别为11.8 nm、13.1 nm、21.0 nm,相对均方根误差分别为0.5%,0.6%、1%,满足系统指标要求,并可在实际系统中集成应用。
1 压电促动器控制算法
1.1 基于广义PI模型的压电促动器前馈补偿
采用广义PI迟滞模型对压电陶瓷迟滞现象进行建模,采用粒子群算法对待求参数进行识别。
1.1.1 广义PI模型
在广义PI迟滞模型中,广义迟滞算子Sr包含2个包络函数,输入函数v随时间增加时,对应广义迟滞算子Sr中的包络函数γl;输入函数v随时间减小时,对应广义迟滞算子Sr中的包络函数γr。由于2个包络函数为不同的表达式,因此,广义迟滞模型可描述非对称及饱和的迟滞现象。图1为广义PI迟滞模型迟滞算子的输入-输出关系示意图。图中,广义迟滞算子在输出z(t)=0时对应的输入值v(t)为ζ1和ζ2,ζ1对应上升阶段,ζ2对应下降阶段。由图可看出包络函数γl和γr是单调函数。
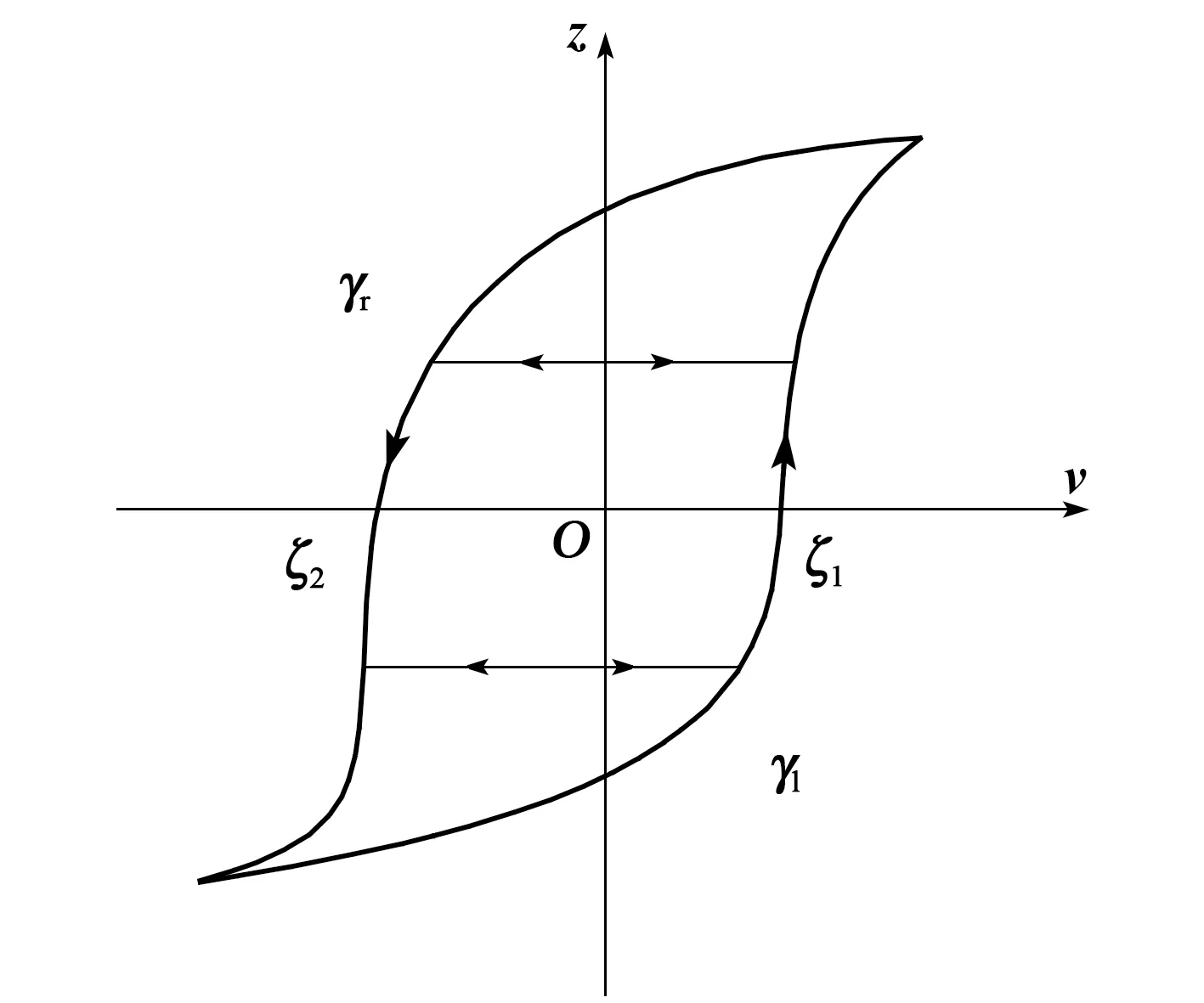
图1 广义PI迟滞算子输入-输出关系示意图
广义PI迟滞模型的迟滞算子可表示为
(1)
式中r为阈值,参照经典迟滞算子决定。本文采用双曲正切函数作为包络函数形式,则包络函数γl、γr的表达式为
(2)
式中a1,b1,c1,d1及a2,b2,c2,d2分别为上升和下降阶段包络函数的待确定参数,可由参数寻优算法辨识得到。
广义PI迟滞模型Φ通过多个迟滞算子Sr和密度函数P(r)的加权叠加来描述相关材料或执行器的迟滞效应。广义PI迟滞模型的输出具体定义Φ[v](t)为
(3)
如式(3)所示,模型是n个广义PI迟滞算子的加权输出结果,P(ri)和ri分别为
(4)
式中:ρ为正数;τ,α为常数。三者均是迟滞算子模型中的待定参数。
因为广义PI迟滞算子Sr是单调的,且密度函数是连续可积的正值函数,由此可得出广义PI迟滞模型在上升、下降沿同样满足单调条件。
1.1.2 迟滞模型的参数识别
广义PI迟滞模型的迟滞算子及密度函数的相关参数通常根据已知的实验数据,采用合适的参数寻优方法得到。粒子群算法在迟滞模型的参数识别中应用较广[14]。粒子群参数优化算法是参数优化、寻找适度函数极值的过程,其可以为不可微的模型进行寻优。其基本过程如下:
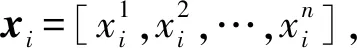
(rand∈random(0,1))
(5)
2) 求每个粒子的适度函数:
(6)
3) 计算个体最优位置pbesti和全局最优位置gbest:
(7)
gbest(k+1)=min{pbesti(k+1)}
(8)
4) 若迭代次数大于itermax,终止计算保存gbest作为最优解;否则根据个体最优和全局最优更新每个粒子的速度和位置向量,退回到步骤2)。
vi(k+1)=w(k)vi(k)+c1r1[pbesti-xi(k)]+
c2r2[gbest-xi(k)]
(9)
xi(k+1)=xi(k)+vi(k+1)
(10)
式中:r1,r2为[0,1]上的随机数;w(k)=0.5+rand/2。
1.1.3 迟滞前馈补偿
对已经建立的迟滞模型进行反演计算,广义PI模型的反演式为
(11)
式(11)分别对上升、下降阶段的包络函数进行反演,其中迟滞算子的具体表达式为
(12)
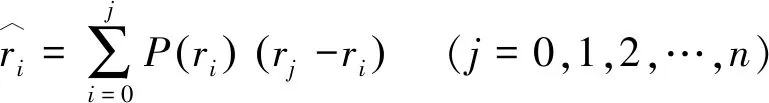
(13)
其中密度函数求解如下:
(14)
式中j=2,3,4,…,n。
1.2 压电促动器复合控制
实验表明,在压电促动器系统中,迟滞特性是影响动态跟踪精度的重要因素,基于广义 PI 逆模型的前馈补偿控制,对于补偿迟滞特性有较好的效果。但压电陶瓷的蠕变特性会令系统的稳态定位发生漂移,而基于比例积分控制率的反馈控制可有效地抑制压电促动器的蠕变影响,保证系统稳态精度。因此,采用复合控制方法能够有效提升系统的动静态跟踪精度。系统框图如图2所示。
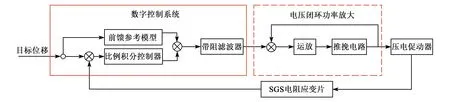
图2 系统复合控制框图
2 实验验证
2.1 实验平台的搭建
为了便于驱动模块在整体系统中的集成,需要压电驱动器成为独立的子系统,这要求模块接口完整并具有集成化、轻小型化等特点。目前广泛采用的基于控制板卡结合计算机操作系统的控制,无论从实时性、集成度及空间、质量都难以满足要求。因此,基于TMS320F28335及XC6SLX45T控制芯片搭建了嵌入式控制系统。其中DSP完成广义PI模型逆模型前馈补偿量的在线计算;FPGA芯片用于完成系统数字闭环控制算法,控制周期采用内部时序控制,可以达到50 kHz,能够实现系统高带宽性能需求,完成高速A/D芯片的采样控制及高速D/A芯片电压输出控制。系统数字架构如图3所示。

图3 系统数控架构示意图
驱动电路由功率放大电路和运算放大器串联组成负反馈放大电路,此外还包括调理电路和电压供电变换电路。采用电压串联负反馈结构,能提高增益的恒定性,减少非线性失真,扩展频带,提高输入电阻,减小输出电阻。功率放大电路采用分立的MOS管搭建推挽电路实现,电压、电流及功率等级可根据负载的大小灵活调整,便于散热及集成化设计,且成本低。国外知名厂商德国PI、法国CEDRAT、美国Thorlabs均是基于分立元件搭建功率放大电路。
压电促动器选用芯明天PSt150/5/7VS10,标称行程9 μm,带SGS电阻应变片的位置信息反馈。采用测微仪对其进行标定后可实时测得系统实际位移。
压电陶瓷驱动器验证样机由上位机、数字控制板、驱动板、供电电源、压电促动器组成。总体框架和实验样机如图4所示。
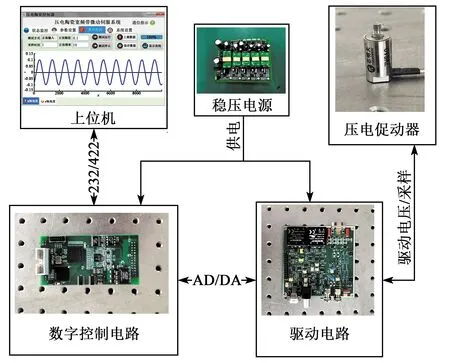
图4 压电驱动器实验验证平台
2.2 控制方法验证
采用开环控制方式分别在给定幅值2 μm、不同频率(50 Hz、100 Hz、200 Hz)的正弦波形得到系统实际输出波形与给定电压间(开环模式下给定位移与实际输出电压为固定比例关系)的关系如图5所示。由图可看出,系统存在较大的迟滞效应,且幅值有较大衰减。
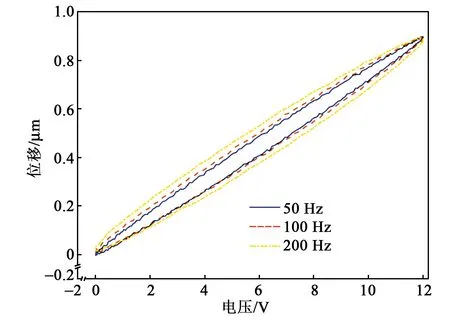
图5 压电促动器迟滞效应
只采用比例积分控制率方式对压电促动器进行闭环控制,分别给定幅值2 μm、不同频率(50 Hz、100 Hz、200 Hz)的正弦波形得到系统实际输出波形与给定目标位移间的关系如图6所示。由图可看出,系统的迟滞效应得到改善,且幅值跟随目标给定相位滞后,随着目标位移频率的增加,相移滞后增大,符合压电促动器伺服控制规律。

图6 比例积分闭环控制下压电迟滞效应
为了进一步改善系统性能,缩小动态误差,采用广义PI模型对压电促动器进行建模,并通过粒子群算法对模型参数进行在线辨识,得到频率分别为50 Hz、100 Hz、200 Hz,幅值为2 μm时广义PI模型的参数寻优结果,如表1所示。

表1 粒子群算法识别所得参数表
电陶瓷促动器在不同频率下的广义PI模型的参数变化不大,且同一组参数应用于不同频率条件下均能起到一定的迟滞抑制效果。采用相同频率和幅值的逆模型可得到最优解,这从一定程度上降低了对DSP实时计算速度的要求。图7为广义PI模型与实际压电促动器模型的迟滞曲线,验证了建模方法的正确性。
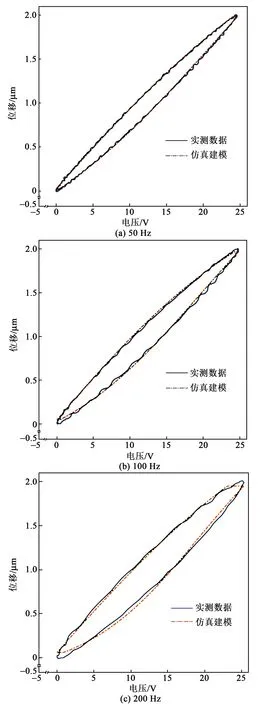
图7 广义PI模型迟滞拟合
采用基于广义PI逆模型的前馈补偿措施,得到前馈跟踪目标轨迹的效果如图8所示。
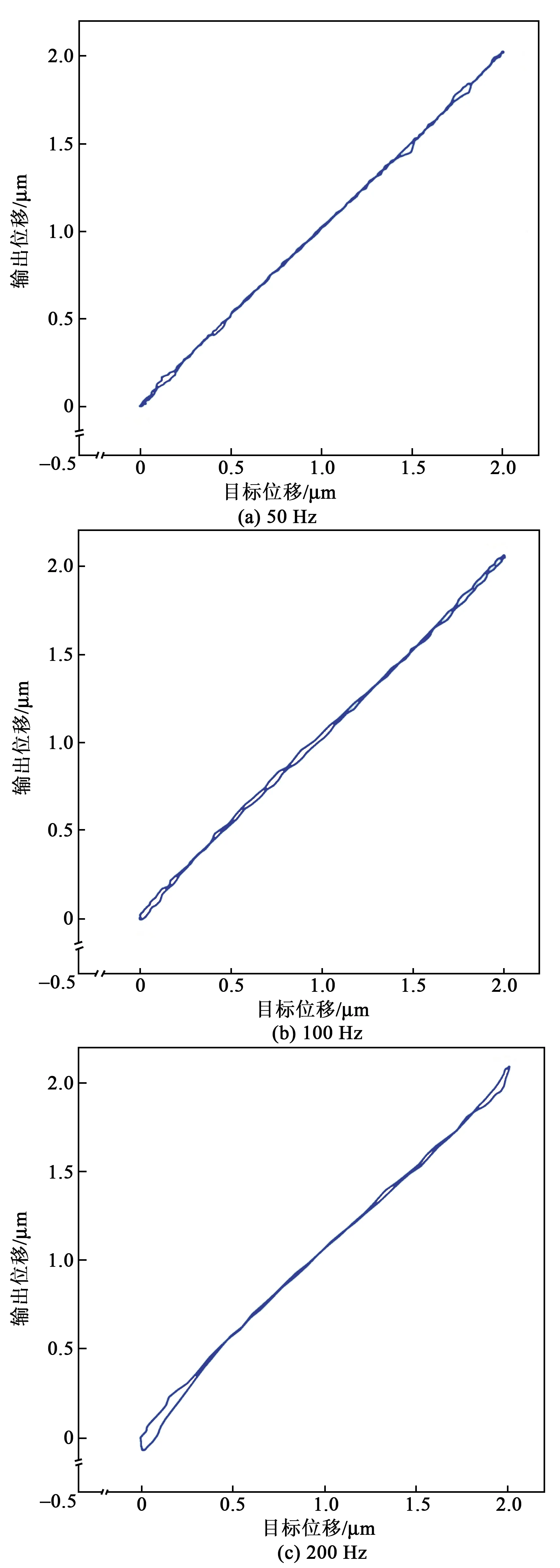
图8 广义PI逆模型前馈控制轨迹跟踪效果
由图8可看出,迟滞现象得到进一步改善,但随着频率的增高,同一周期系统采样点逐渐稀疏,模型拟合度逐渐下降,因此,相对于低频控制效果,高频非线性度逐渐增加。
图9为采用广义PI逆模型前馈补偿结合比例积分控制的复合控制效果图。相对于单独采用前馈控制和反馈控制,迟滞效应得到了充分抑制。为了量化模型表现,采用均方根误差erms、相对均方根误差enrms和迟滞比H作为指标来评价控制方法的跟踪效果,即:
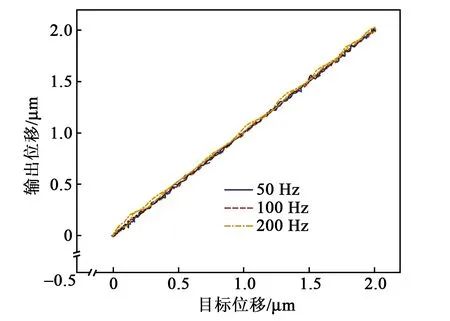
图9 复合控制轨迹跟踪效果图
(15)
(16)
(17)
式中:yd为目标位移;y为输出位移;p为采样点个数;yl,yr分别为同一目标位移指令下的上升、下降沿输出位移值。由式(15)~(17)得到误差分析表,如表2所示。
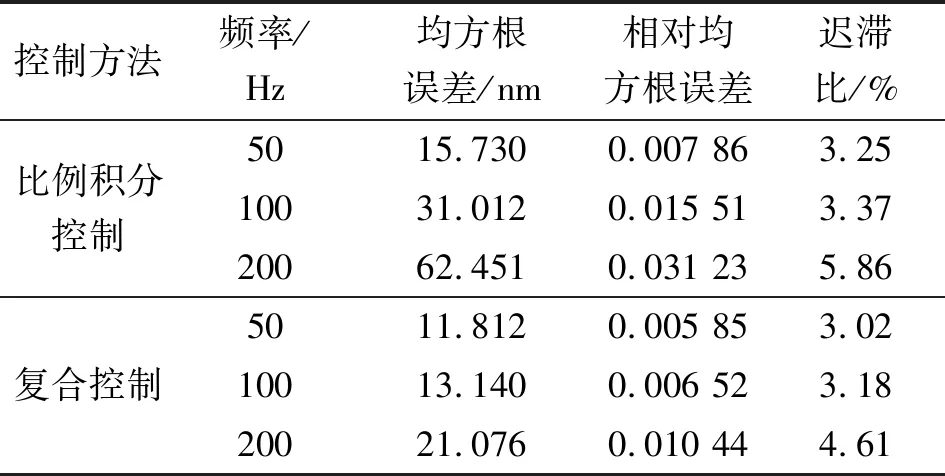
表2 误差分析表
实验结果表明,本文所提压电驱动器设计方法对压电促动器的动静态控制精度均有提升,以GPI模型为基础构建的前馈算法相较于微分方程迟滞模型和其他算子模型,在保证模型精度的前提下,模型反演更简单,参数数量较少。在集成到硬件系统实现迟滞补偿时更便捷、高效。
3 结束语
基于广义PI模型及粒子群辨识算法,本文提出了一种压电促动器复合控制方法,结合嵌入式数控芯片及分立式功率放大电路,设计了一款压电驱动器。该压电伺服系统动静态跟踪精度得到了显著提升,响应频宽大,且便于系统集成,可以进行工程化应用。
