高结构对称性微半球陀螺设计与制造

梅 松,杨 峰,文 路,卢昱瑾,贺韵祺,陈朝春,韩世川,雷 霆,林丙涛

(1.中国电子科技集团公司 第二十六研究所, 重庆 400060;2.重庆市固态惯性技术企业工程技术研究中心,重庆 401332;3.重庆市固态惯性技术工程实验室,重庆 401332)

0 引言

采用易于批量化制造的微吹制/微加工工艺制造的微半球陀螺,其具有高精度、低噪声、小体积及低成本等优点[1-2],是高性能微型陀螺热门的发展方向之一。与传统半球陀螺相比,微半球陀螺尺寸大幅减小,因而制造误差对性能的影响更突出,且谐振子成型所采用的微吹制工艺为新型特种工艺[3],其误差检测与抑制技术不能满足设计要求,制约了陀螺性能的进一步提升。

由于微半球陀螺工作在四波腹模态,其四阶质量不对称是引起陀螺性能劣化的一项主要因素。密歇根大学、加州大学欧文分校及国防科技大学等提出了多种四阶质量不对称的辨识与修调技术[4-6],但对陀螺1～3阶(低阶)质量不对称的影响研究较少,受限于微半球陀螺的结构及工艺特点,其低阶质量不对称的修调难以实现。另一方面,四阶质量不对称修调工艺有可能进一步增大低阶质量不对称,从而增大谐振子锚点损耗,引起谐振子品质因数(Q)值劣化。因此,提高谐振子初始制造精度及降低低阶质量不对称是提升陀螺性能的前提条件。

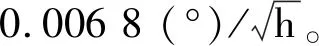
1 微半球陀螺结构设计及误差建模

1.1 微半球陀螺结构设计

微半球谐振子具有轴对称结构,其厚度和曲率半径沿截面方向连续变化。通过对比火焰吹制不同工艺参数下形成的谐振子CT图像特征,建立壁厚、曲率分布与壳体直径、锚点直径、基片厚度及吹制高度等参数的对应关系,即可实现谐振子三维几何建模,谐振子截面轮廓原始图像及提取特征方法如图1所示。

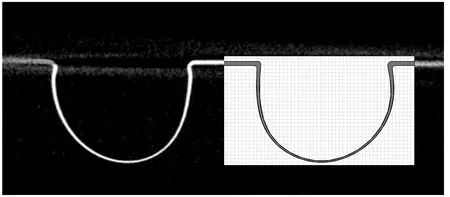
图1 CT扫描原始图像和提取轮廓特征对比

本文采用平面电极结构形式构成微电容结构,为了增加电容面积,提高陀螺机械灵敏度,同时有利于质量调平工艺的实现。因此,在谐振子唇口沿圆周方向均布48个齿状质量块结构[7],采用Comsol Multiphysics软件构建三维模型,对谐振子圆形锚点面施加固定约束。基于瑞利能量法进行模态仿真计算,前6阶振动模态如图2所示。

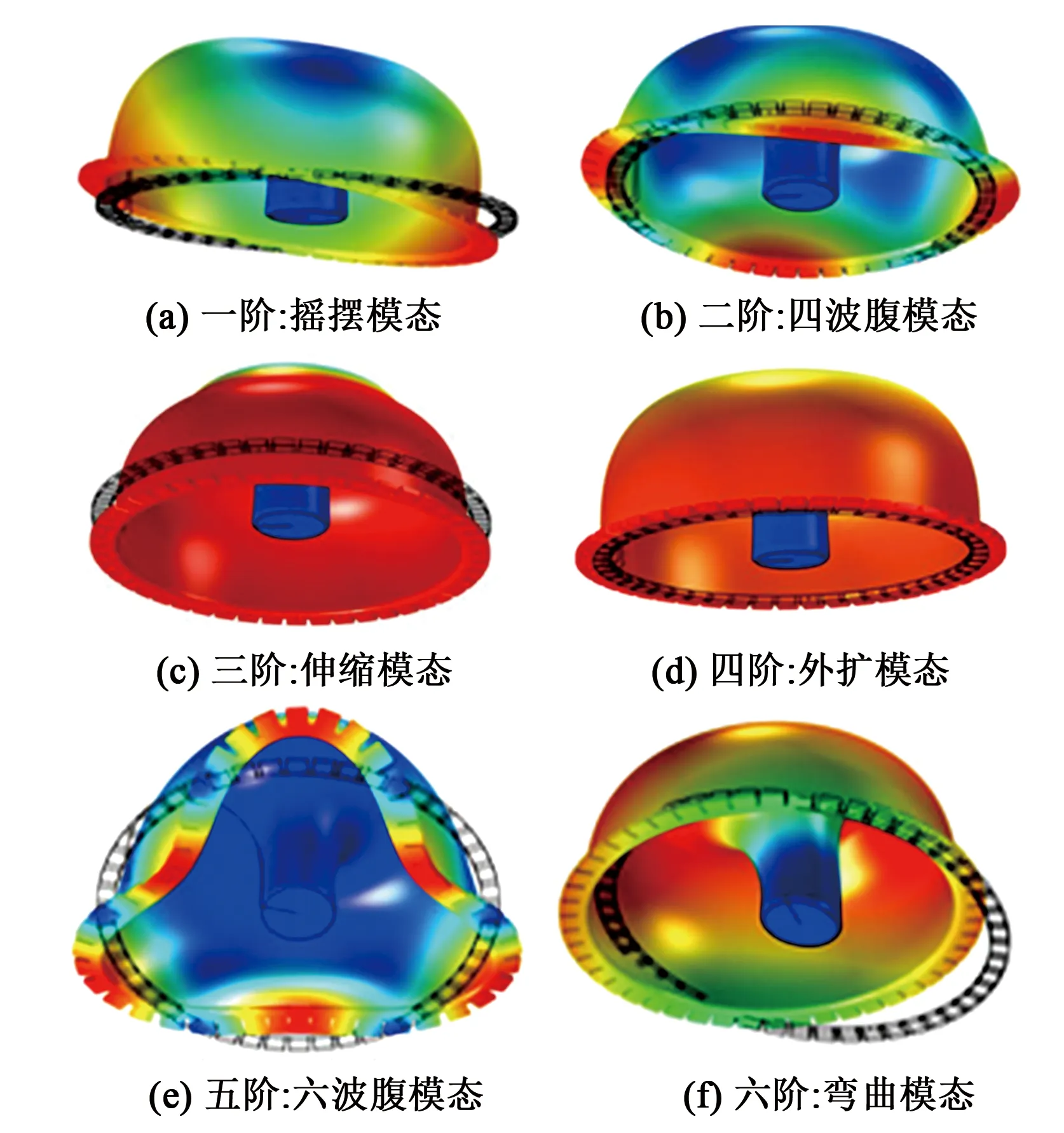
图2 微半球谐振子前6阶振动模态

综合考虑谐振子尺寸、模态频率、机械灵敏度及结构强度等因素,最终设计的结构参数如图3所示,其工作模态频率为5 927 Hz。

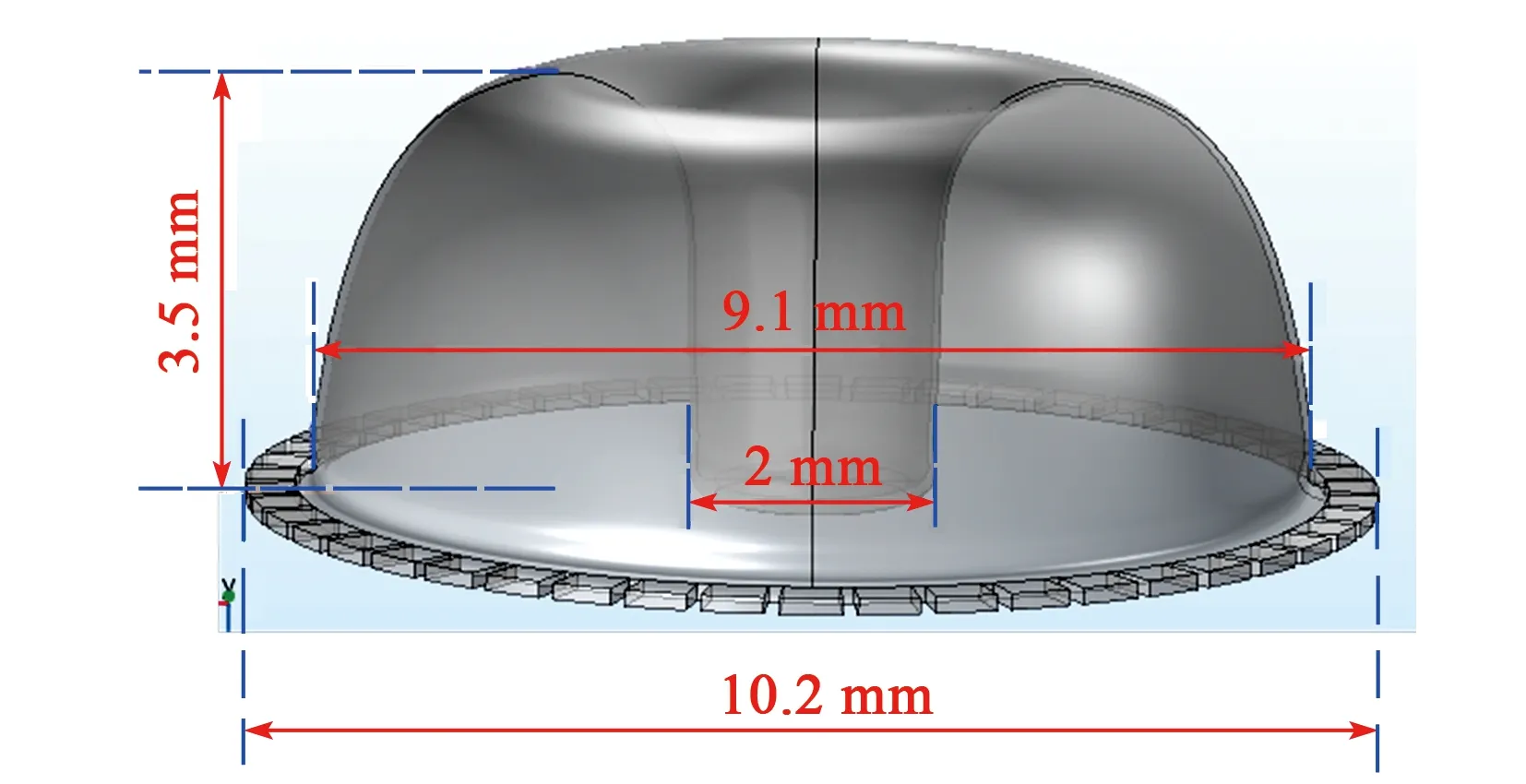
图3 微半球谐振子结构参数

1.2 微半球陀螺误差建模

在微半球谐振子的火焰吹制成型过程中,温场均匀性是引起谐振子结构对称性误差的最主要因素,由中心对准精度、火焰形貌精度及火焰垂直度等带来的加工误差易引起谐振子的一、二阶质量不对称,其误差示意图如图4所示。

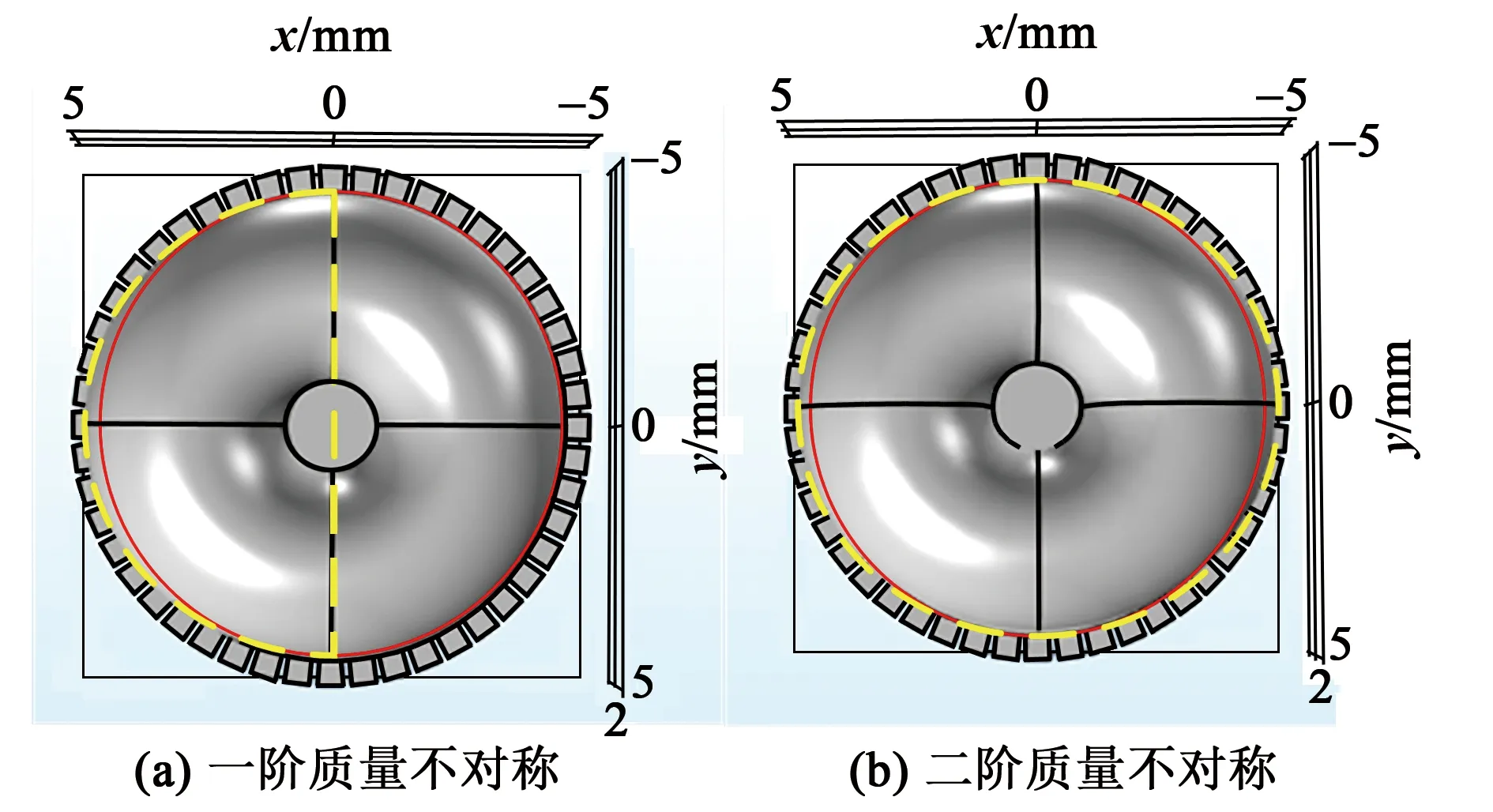
图4 微半球质量不对称模型

缺陷存在的情况下,谐振子锚点与其四波腹振动时质心的轴线不重合,将导致陀螺工作时锚点损耗增加,进而影响Q值。为分析结构误差对Q值的影响,建立了包含完美匹配层(PML)[8]的微半球陀螺锚点损耗误差模型,如图5所示。

图5 PML锚点损耗模型

完美匹配层是用于吸收机械波,避免其反射能量干扰Q值计算的模型区域。在计算模型中,与谐振子连接的基底被设计为半球体结构,采用四面体网格构建PML网络模型,定义其材料为石英玻璃,半径为RPML,内半径rPML表征锚点中心到衰减区域的距离,RPML-rPML为吸收区域的深度。为减少网格划分对Q值计算的影响,RPML的尺寸不能远小于振动产生的机械波波长,石英玻璃中体纵波传播速度为

(1)

根据石英玻璃材料参数及谐振子工作频率,可得其纵波波速约为5 906 m/s,纵波波长约为996 mm,设RPML=160 mm,rPML=120 mm,PML比例因子为1,模型中rPML始终大于20个网格长度。将PML的边缘作为固定约束边界,其他边界作为自由边界。采用Comsol Multiphysis软件的计算谐振子的特征频率,其各阶模态的Q值为

(2)

式中Re(ω),Im(ω)分别为角振动频率ω的实部和虚部,这些值都可在计算结果中直接提取。

为了分析结构缺陷对锚点损耗Q值的影响,本文采用图3所示的结构参数计算理想条件下的锚点损耗Q0作为基准值,然后再计算图4所示的非理想结构下锚点损耗Q1。由于计算过程忽略了谐振子振动阻尼,因而Q0、Q1的绝对值与实际谐振子Q值无法直接对应,采用Q1/Q0的值作为分析影响结构对称性的主要参数。

在一阶质量不对称模型中,定义结构不对称系数为

(3)

式中:R为模型初始半径;R1为引入结构误差后的局部半径。仅改变R1,其他参数保持不变,计算其模型中四波腹模态Q值。分别统计四波腹模态的两个简并模态Q1/Q0受一阶质量不对称性变化的影响规律,如图6(a)所示。同理也可统计二阶质量不对称模型两个简并模态下Q1/Q0的变化规律,如图6(b)所示。

图6 η对四波腹模态的两个简并模态Q值的影响

由图6(a)可看出,随着一阶结构不对称系数η的增加,四波腹模态低频轴锚点损耗Q值表现出降低的趋势,高频轴锚点损耗Q值变化不大,这是因为模型中局部质量增加的位置表征了四波腹模态低频轴的方位角。这说明一阶的结构不对称会降低其相应位置刚性轴Q值,进而引起谐振子周向Q值的不均匀。同样的现象也存在于二阶结构不对称的模型。对比图6(a)、(b)可看出,二阶的结构不对称对Q值均匀性影响比一阶影响更显著。由于微半球陀螺一、二阶的结构不对称误差难以通过质量修调工艺进行修正,其误差水平主要依赖于火焰吹制工艺的控制精度,而量级在微米尺度的吹制误差难以被准确辨识,限制了吹制平台误差修正工作的开展。因此,本文进一步设计了一种微半球陀螺吹制误差辨识方法。

2 微半球陀螺结构误差辨识及工艺优化

辨识微半球陀螺的1～4阶结构不对称误差,首先需要在谐振子的某一圆周截面上采集足够多的数据点,得到各点的圆周角θ,以及各点到截面拟合圆心的距离r′,将坐标点按圆周角展开成傅里叶级数形式:

(4)

式中:εk为圆周上第k阶结构不对称的误差量;θk为第k阶结构不对称的相位。

统计谐振子多个截面的εk和θk,即可整体评价谐振子的结构对称性误差大小及误差相位。由于传统的三坐标测量仪存在探头尺寸大,测量效率低,测量力易引起壳体形变的缺陷,不适用于微半球谐振子的结构误差辨识。本文采用德国业纳C305轴类光学测量系统构建了非接触式误差测量平台,如图7所示。

图7 非接触式微半球谐振子误差测量平台

被测样品固定在测量平台上绕轴旋转,电器耦合器件(CCD)相机对截面轮廓信息进行连续采集,最终形成微半球谐振子截面轮廓,设备每旋转0.1°,采集一组轮廓数据,圆度测量精度为1 μm。对抽取的3个谐振子样品靠近唇口的相同高度截面进行轮廓数据采集,获得其半径在圆周方向上的不均匀分布数据,对其做傅里叶级数展开,统计其圆度误差及1～4阶结构不对称误差量εk,如图8所示。

图8 3个谐振子样品同一截面处的结构不对称误差

图8中,圆周方向的轮廓分布图是将尺寸误差放大100倍后绘制的。结合傅里叶展开后得到的误差系数可以看出,最大的误差来源是二阶结构不对称,二阶结构不对称主要与火焰形貌精度、火焰垂直度及成型模具加工精度相关。通过统计εk和θk在各截面的分布,可依次对火焰吹制平台的上述各项误差进行调试和修正:首先找到误差最大阶次对应的相位角;设计正交实验,对上述可能的误差进行参数微调,找到与该相位角变化相关性最高的参数进行修正;再统计新的误差最大阶次对应的相位角,开展新一轮迭代优化,多次迭代直到接近平台修调的精度极限。

抽取修正平台误差后吹制的3个谐振子样品,在相同高度的截面上采集的结构不对称误差数据,如图9所示。

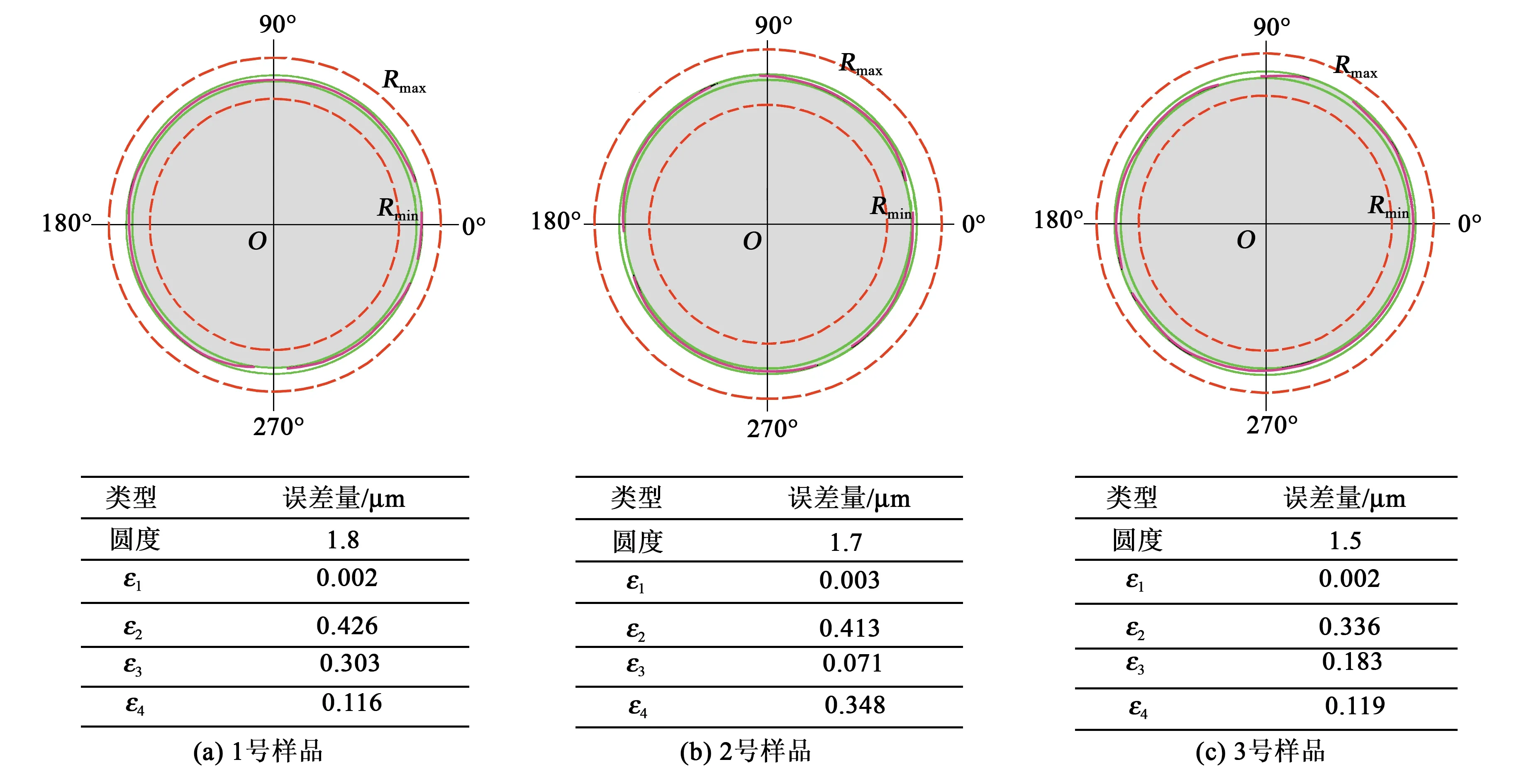
图9 工艺优化后3个谐振子同一截面处的结构不对称性误差

对比图8、9可看出,工艺优化后微半球谐振子结构对称性明显提升,有助于提升陀螺的Q值及Q值均匀性。

3 测试结果

根据前文所述设计及工艺方法制备了高对称性微半球谐振子样品,完成平面电极装配后如图10(a)所示。制作出真空封装后的微半球陀螺表头样品,如图10(b)所示。

图10 微半球谐振子样品及微半球陀螺表头

在速率模式下调整微半球陀螺四波腹模态的驻波位置,每间隔10°采用自由衰减法测量1组Q值。其中0°电极位置的驻波断电后振幅随时间的衰减曲线如图11(a)所示,其谐振频率为6 361.58 Hz,时间常数为45.46 s,Q值为9.097×105;统计0°～90°各电极位置的Q值分布,如图11(b)所示。由图可以看出,在0°～90°时陀螺Q值呈正弦分布规律,Q值均匀性为±0.87%。

图11 微半球陀螺Q值测试结果及周向Q值分布

测试了速率模式下陀螺样机的性能,设置量程为±20 (°)/s,带宽为5 Hz,将陀螺接通电源预热20 min后,连续采样1 h(采样周期为1 s)。室温环境下陀螺样机的零偏输出如图12所示,采用10 s平滑的方式处理数据[9],得到陀螺零偏稳定性为0.108 (°)/h。

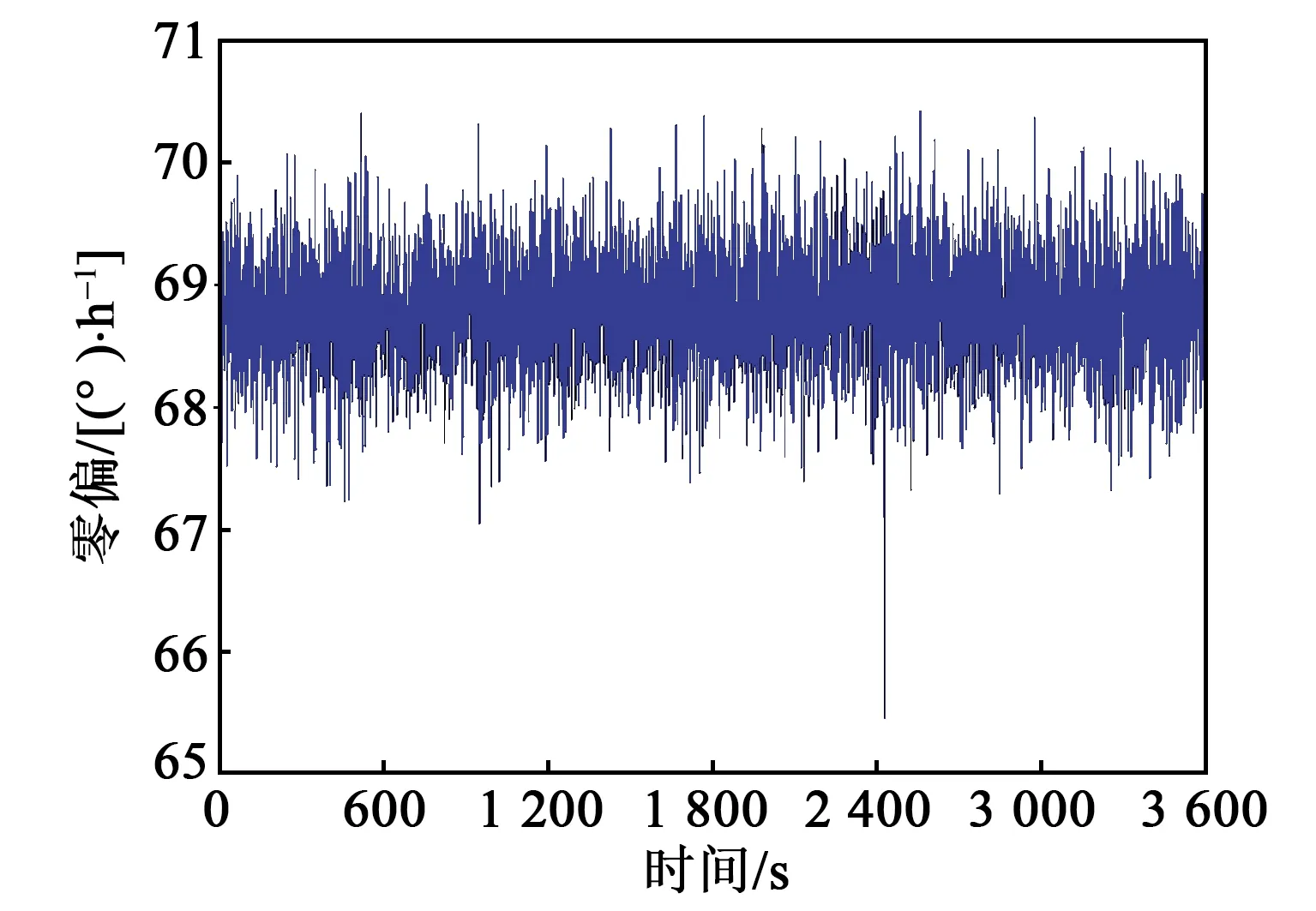
图12 微半球陀螺零偏输出数据

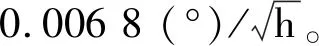
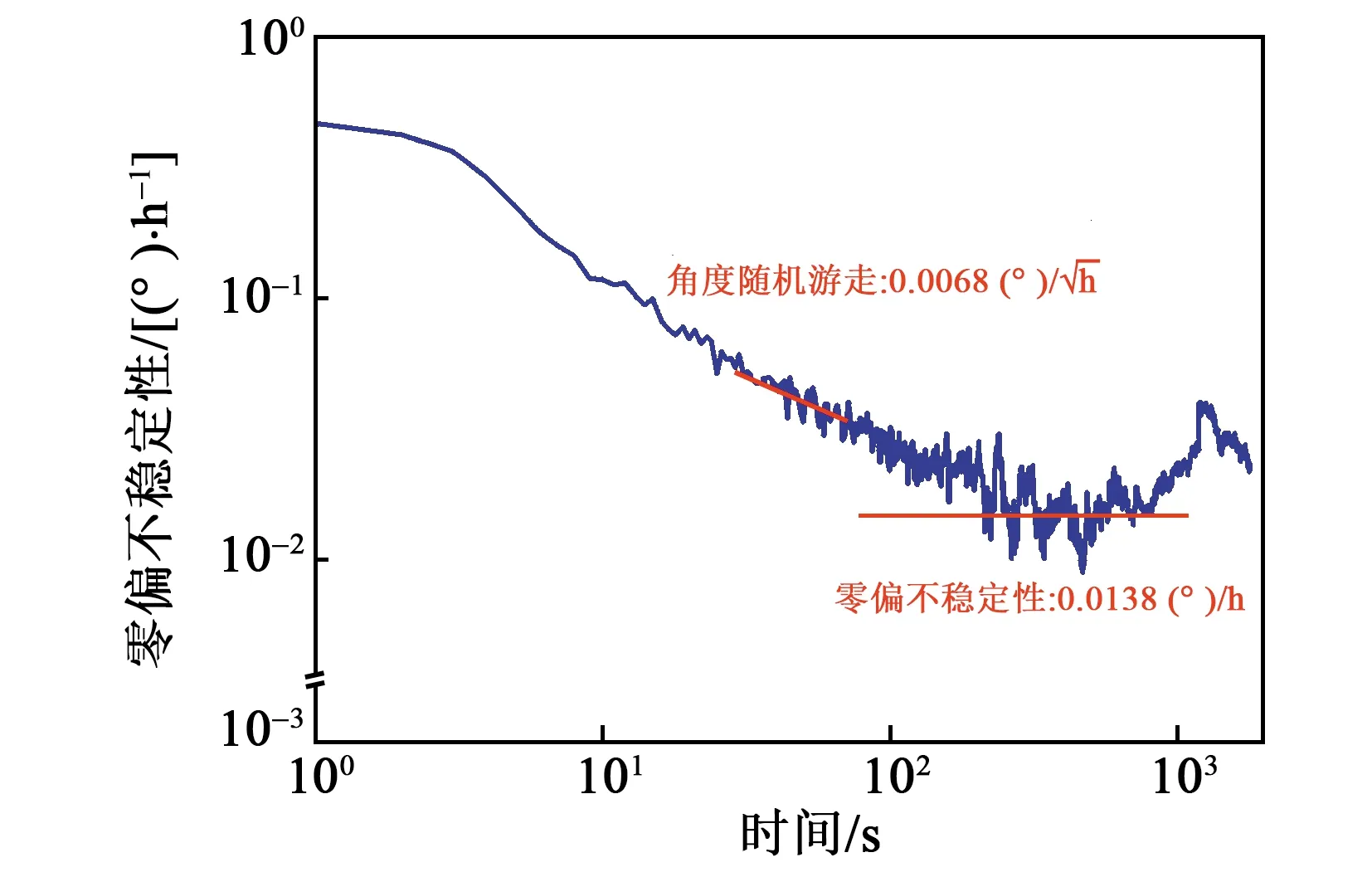
图13 Allan方差曲线图

4 结束语

微半球谐振子制造误差的准确辨识与抑制,是微半球陀螺进一步提升性能水平的关键。本文建立了微半球陀螺结构误差对Q值均匀性影响的有限元模型,提出了结构误差的评价方法,实现了误差检测及工艺优化,制备的谐振子圆度误差≤2 μm,谐振子低阶质量不对称性得到明显改善,提升了陀螺样机的Q值均匀性及精度水平。但受限于谐振子结构释放、清洗、薄膜沉积等工艺引入的表面缺陷及均匀性误差,陀螺整体性能仍有提升空间,下一步工作将对上述工艺开展更深入的研究,从宏观结构对称性和微观结构均匀性两方面整体提升微半球陀螺制造精度。