Exploring effects of property variation on fragmentation of metal rings using a simple model

J.D.Robson

Department of Materials, The University of Manchester, Manchester, M13 9PL, UK

Keywords:Fragmentation Mott model Property variation

ABSTRACT A simple finite element implementation of the Mott model for fragmentation of a thin walled ring has been implemented and used to explore the effect of local variations in fracture strain around the ring.The model has successfully reproduced the fragment size distributions previously reported,which follow a characteristic “Mott distribution” form,providing sufficient (1000) simulations are run.It has been shown that this form is retained even when there are large differences in the random distribution of fracture strains or a different choice of function used to describe the fracture strain scatter.In these cases,the strain rate has a much stronger effect than fracture strain distribution the on the average fragment size and fragment distribution.However,for cases where there are a small number of local defects that strongly reduce the fracture strain at certain locations around the ring,the predicted fragment size distribution develops a bimodal character.This is also the case for large but gradual variations in fracture strain with position around the ring.The results have implications for cases where a small number of large pre-existing defects exist,or processing has led to macrozones in the microstructure.The utility of a simple fast running model to study these cases is discussed.

1.Introduction

The ability to predict the size and distribution of fragments when a cylindrical shell is rapidly expanded in the radial direction has been a long-standing goal of researchers for over 75 years [1].Early work by Mott[1,2]established that in such cases there is to be expected a characteristic distribution of fragment sizes,which is related to the imposed strain rate,material properties,and property scatter.

The modern approach to modelling fragmentation involves finite element(FE)simulations which have the advantage of being able to generalize to the realistic geometries and dynamically evolving loading conditions that reflect the complexity of explosively loaded expanding tubes[3-6].Even with such sophisticated models,reliably predicting fragmentation in ductile materials remains a considerable task,both as a result of numerical difficulties and the highly complex failure mechanisms that occur at high strain rate[7,8].Predicting where the fractures will initiate remains a significant challenge.This can be addressed by randomly preassigning damage to the material [5],or relying on numerical instabilities to initiate fractures[4].In either case,this is not related to the real heterogeneities in the microstructure or initial defects that initiate fracture.An additional constraint of a sophisticated FE simulation is the high computational overhead and relatively long run times,making systematic parametric studies time consuming.

Classical analytical models(such as that of Mott[1,9]and Grady[10])are more limited in capability and require making simplifying assumptions.Nevertheless,such classical models have been shown to predict experimental fragment size distributions (FSDs) quite well [11].Various extensions have been made to the Mott method in an attempt to improve accuracy of prediction for both the smallest [12]and largest fragments [13],where the observed deviation from the Mott FSD observed is greatest.

An advantage of the Mott method is that the relationships between the material parameters and the FSD is immediately apparent.Furthermore,since such models can be run very rapidly,they can be used to quickly perform parametric analysis.Therefore,there remain scenarios where classical fragmentation models retain important advantages over more complex FE approaches[14].

Both FE and classical models rely on making assumptions about the homogeneity and distribution of the material properties that control fragmentation.For example,in Mott’s original work,the positions where fracture could occur were pre-defined randomly.It is also common to assume that the property of importance (for example,the fracture strain) follows a well behaved statistical pattern(for example,a Weibull distribution) [2].

In practice,however,this may not be the case.If fragmentation is initiated by pre-existing flaws(voids or cracks),this damage may be clustered around one location and fracture initiation is not randomly located.If fragmentation is controlled by the microstructure or pre-existing defects,then this can vary in non-random ways,even over long length scales.For example,elemental segregation can lead to regions with different compositions and hence different properties(macrosegregation,e.g.Ref.[15]).Variations in grain size or texture can also occur over the macro-scale (e.g.macrozones [16]).Defects such as cracks or porosity are often clustered (e.g.Ref.[17]).

In principle,all of these aspects can be investigated using a high fidelity FE simulation,but as discussed this is very time consuming and may not reveal the dependencies of fracture on material property variation in a simple and transparent way.Instead,the Mott approach can be extended to explore the effect that nonrandom damage will have on fragmentation behaviour.The development of such a model and its application to predict the effect of damage distribution on the resultant FSD was the objective of the current work.

2.Model development

The model developed in this work is based on the physics-based statistical fragmentation theory developed by Mott[1].The origins of this model,its various extensions,and its applications are discussed in detail by Grady [2].The Mott model treats a rapidly expanding,thin walled ring,which is reduced to a 1-dimensional problem.The material from which the ring is made is considered to be rigid/perfectly plastic and subject to radial expansion at a constant velocity.The Mott method only applies when the ring is sufficiently thin that the damage causing fragmentation occurs near the surface and the resultant cracks coalesce with the free surface before they coalesce with each other [8].

To briefly recap,the Mott model is based on a configuration as shown schematically in Fig.1.It is assumed there is a variation of critical strains to fracture randomly distributed around the ring.When the imposed strain due to the expansion exceeds the lowest fracture strain,the first fracture will occur(marked 1 in Fig.1).This will produce a relaxation wave (Mott wave) leading to an expanding region surrounding the fracture that is no longer under stress and therefore immune from further fracture.The wave expands with parabolic kinetics (i.e.the velocity of the wave decreases with increasing time).Meanwhile,other fracture points will activate in turn (e.g.2 then 3),which will also produce growing relaxed regions.Eventually,the whole ring is relaxed,at which point fragmentation is complete.The fragmentation process is controlled by the variation in fracture strain with imposed strain and by the velocity of the Mott wave.

Fig.1.A schematic of the 1-dimensional Mott problem.Fracture occurs at random sites in turn (1,2,then 3) and waves originate at points of fracture and propagate at finite speed relieving tensile stresses in the surrounding regions(shaded grey).Further fracture is only possible in regions that are unrelaxed (unshaded).

In the model as developed by Mott,the scatter in fracture strains(hazard function)is assumed to follow an exponential law such the probability of a fracture occurring in a unit length with an increment in strain dε is given by

whereCand γ are constants that characterize the distribution of fracture strain.Other assumptions about the distribution of fracture strains can also be used,such as the Weibull distribution,and this will be discussed in more detail later.Note that Eq.(1)has no strong physical basis but provides a functional form that allows the increment in probability of fracture to increase with each increment in strain either strongly or weakly depending on the choice of the γ parameter,as will be demonstrated later.

The probability of a new fracture occurring anywhere in the ring therefore increases with an increment strain dε according to

whereris the radius of the ring andfis the fraction of the ring that remains unrelaxed by Mott waves (i.e.is able to participate in the fracture process).

All material points are assumed to follow the same law,so the position of the fractures is not predicted but has to be randomly pre-assigned.As the fraction of the ring relaxed by the passage of Mott waves increases,the probability of further fracture is reduced(for a given level of strain).The size of the relaxed regions can be calculated as a function of time (t) from the velocity of the Mott waves by

where σyis the yield stress,ρ is the material density,and v the radial expansion velocity.

Mott used a graphical technique to determine the FSD using these principles,but the advent of the computer also allows this to be determined iteratively for a very large number of rings,giving the required statistics[9].One limitation of all of these methods is that the material properties (e.g.failure strain) at each position around the ring are determined by the same statistical relationship.However,in practice,underlying variations in the defect distribution,microstructure,or texture around the ring can lead to systematic variations in fracture strain with position.Locally,on the micro-scale,the material behaviour at each point is not the same.Therefore,in the present work,a spatially dependent fracture strain is introduced.

The method is a simple 1-dimensional finite element approach in which the ring is divided into a large number of elements(100-1000 elements was found to be sufficient for convergence).Each element has its own fracture strain,which is assumed to be constant.The fracture strains can be chosen from a statistical distribution (e.g.Mott or Weibull) or arbitrarily assigned to each element.This enables (for example) the effect of having certain regions containing pre-existing flaws(i.e.low fracture strain)to be simulated.The model runs numerically,and at each time step the strain in the unrelaxed portion of the ring is compared with the fracture strains in each element to determine which elements will initiate fracture in that step.The time-step was reduced until a convergent solution was reached,leading to steps in the range 2-6 ns.Once fracture starts in an element,it will relax the surrounding elements controlled by the growth velocity of the Mott waves(Eq.(3)).Fracture of these relaxed elements will therefore not occur.Following Mott,it assumed that the fracture process is very rapid and the material behaves perfectly plastically.The simulation completes when all the elements are relaxed.The model is implemented in MATLAB.

As demonstrated by Wesenberg and Sagartz[9],a large number of simulations need to be run to produce a convergent FSD.They demonstrated that 1000 simulations led to a smooth FSD,whereas running the model for only 100 rings still produced considerable scatter in the results [9].In the present work,1000 simulations were performed in each case.This was found to lead to a convergent FSD.

To enable the results to be compared with the numerical simulation and experimental data of Wesenberg and Sagartz [9],the same assumptions about the material and geometry of the rings were used.The ring material is AA6061-T6,which is taken to have a yield strength of 240 MPa and density of 2700 kg/m3[18].The quasi-static strain to failure of this material in a tensile test is around 12%[18].The ring outer diameter is taken as 0.127 m.Note that the predictions are not sensitive to the precise choice of these parameters.

3.Results

The model is first compared with the experimental data and simulation results performed by Wesenberg and Sagartz [9].The Mott function (Eq.(1)) was used to describe the fracture strain probability distribution,with a value of γ=20.The model is sensitive to strain rate and the strain rate at fracture is not known(the initial nominal strain rate was 104±5×102s-1).Therefore,this was used as a calibration parameter (which,as shown later shifts the FSD up or down in size).Using a strain rate of 3.16× 103s-1gave good agreement between the results of the present model,the predictions of Wesenberg and Sagartz,and the experimental data(Fig.2).An important parameter defined by Mott is the characteristic lengthx0(see Ref.[1]for the definition of this parameter).The optimized strain rate here gives a corresponding value of（2πr）/x0=13.4,where 2πris the ring circumference.Finally,it must be noted that the experimental data is compiled from only 11 rings.As demonstrated by Wesenberg and Sagartz,at least 1000 rings are needed to produce a converged FSD.Therefore,there is expected to be a large scatter in the experimental results and the apparent minimum due to one point in the experimental distribution is likely to be a result of this scatter rather than evidence of a truly bimodal distribution.

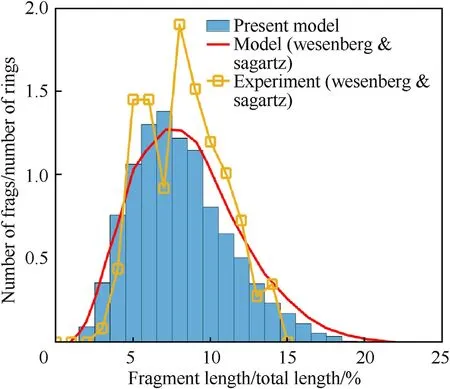
Fig.2.Predicted FSD compared with the modelling results (1000 rings) and experimental data of Wesenberg and Sagartz [9].

As the Mott model is very simple,the only variable that captures the effect of the imposed conditions is the ring expansion velocity(which determines the strain rate).The effect of strain rate on the prediction of the fragment size distribution is shown in Fig.3.This simulation assumes the critical strain to form fractures is independent of the strain rate,which has been shown to be reasonable once a threshold strain rate is exceeded(as is the case here)[4].As expected,a higher strain rate leads to smaller fragments and a tighter distribution of fragment sizes.The average fragment size is also decreased with increasing strain rate as expected [1].For example,the mean and mode fragment size decreases from 11%to 4%of the total circumference length with increasing strain rate.The average fragment size is also expected to be directly related tox0.For the results here,the average fragment length increases from 1.6x0at the lowest strain rate to 2x0at the highest strain rate.In previous implementations of the Mott model,the average fragment length is reported as varying from approximately 1.5x0to 1.8x0[1,2].An analytical value for the average fracture length ofwas derived by Grady[2]using a modified fracture law that is different to that used here.Given the uncertainty in the average fragment size associated with the discretization of the FSD into size bins necessary in the present work,the relationship between the average fracture length andx0is in reasonable agreement with this previous work.

Fig.3.Predicted FSD with changing strain rate relative to the reference strain rate.

As demonstrated by Mott [1]and discussed extensively by Grady[2],the material property that controls the shape of the FSD is the scatter in failure strains.For example,if the fracture strain was identical everywhere in the ring (no scatter),then the Mott model would expect all points in the ring to break simultaneously.A wide scatter causes some regions to be susceptible to fracture at lower strains than others,and once the initial fracture occurs the relaxation of the surrounding material prevents it from further fragmentation.The FSD is thus a direct consequence of the distribution of fracture strains.

The shape of the function determining the distribution of fracture strains(Eq.(1))is controlled by the parameter γ.A value of γ of 128 gives a root mean squared scatter of 1%in the strain to fracture,which is typical of that observed in a tensile test.However,the scatter in quasi-static tensile tests is expected to be much less than in a high strain rate ring expansion test since in quasi-static testing extensive work hardening can locally resist failure due to defects.Good fits to real FSDs are obtained using much lower values of γ[2].Mott considers γ values in the range 20-67 for various different Fe-C alloys.The value of γ for AA6061-T6 used by Wesenberg and Sagartz also falls below this range (this is not explicitly stated in their work but can be estimated from their fit forx0(the characteristic fragment length[1])as ⋍5).The effect of changing γ on the probability of fracture distribution with strain and the FSD is shown in Fig.4.The probability of fracture was scaled between 0 at a strain of 0.1 and 1 (100%) at a strain of 0.2.

Fig.4.(a) Probability of fracture with increasing strain for different values of γ in the Mott hazard function.(b) Predicted FSD for the functions shown in (a).

The effect of changing γ on the probability of fracture with increasing strain is shown in Fig.4(a).Values of γ of 10 or less give a probability of fracture that scales near linearly with increasing strain.Increasing γ leads to an increase in the rate at which the probability of fracture increases with strain.These different behaviours give different FSDs,as shown in Fig.4(b).Although the larger γ value gives a greater spread in the fragment lengths,which is expected,it is noteworthy that even large differences in γ give quite small changes in the mean,mode,and maximum fragment size.For example,for γ=10,the mean,mode,and maximum fragment sizes (as a fraction of the total circumference length) are 7%,7%,and 20%respectively.For γ=80,the corresponding values are 10%,10% and 22%.

An alternative to the Mott hazard function is to assume that the probability of fracture follows a more general Weibull distribution[2].In this case,the cumulative distribution function (the probability of failure with increasing strain) is given by

where the shape and scale parameters arekand λ respectively.As shown by Grady [2],the FSD arising from using the Mott or generalized Weibull distribution can be near identical with suitable choice of parameters.A typical value forkto capture the variation in fracture strain in metals would bek⋍12.The effect of changing this parameter on both the probability of failure with strain and the resultant FSD is shown in Fig.5.As shown in Fig.5(a),a high value ofkleads to a narrow distribution of fracture strains and a low value a wide distribution.However,Fig.5(b)shows that even with the large differences in the distribution of fracture strains,the resultant FSDs are quite similar (Fig.5(b)).As expected,the FSD is broadest when the probability of fracture distribution is also broadest.

Fig.5.(a) Probability of fracture with increasing strain for different values of k for a Weibull distribution of fracture strains.(b) Predicted FSD for the functions shown in (a).

The finite element implementation of the Mott model developed here enables the effect of spatial variations in fracture strain to be explored.This is more representative of the most common physical process of metal fracture in microstructures that contain defects.Defects can take the form of pre-existing voids,cracks,or(for example)brittle intermetallic particles.Such defects can lead to regions where the local fracture strain is less than the overall fracture strain that would be determined from a tensile test.Furthermore,these regions may be clustered together or uniformly distributed.There can also be long-range variations in the fracture strain due to long-range composition variations (e.g.due to macrosegregation) or texture change (e.g.macrozones).For these simulations,the baseline distribution of fracture strains was assumed to follow that used to produce Fig.2(Mott hazard function,γ=20).Element specific changes were then made to the fracture strain to explore various defect scenarios.In each case,1000 simulations were run to obtain good statistics for the FSDs.

In the first simulation,it was assumed that pre-existing defects were present in 1,2,or 3 elements such that the fracture strain was reduced by 50%in these elements.This is a very large reduction in fracture strain,but such effects can be produced by harmful defects such as inclusion particles or cracks.The results of this simulation are shown in Fig.6.An increase in the number of defective elements leads to an increase in the spread of the FSD.Furthermore,the shape of the distribution changes and becomes bimodal.

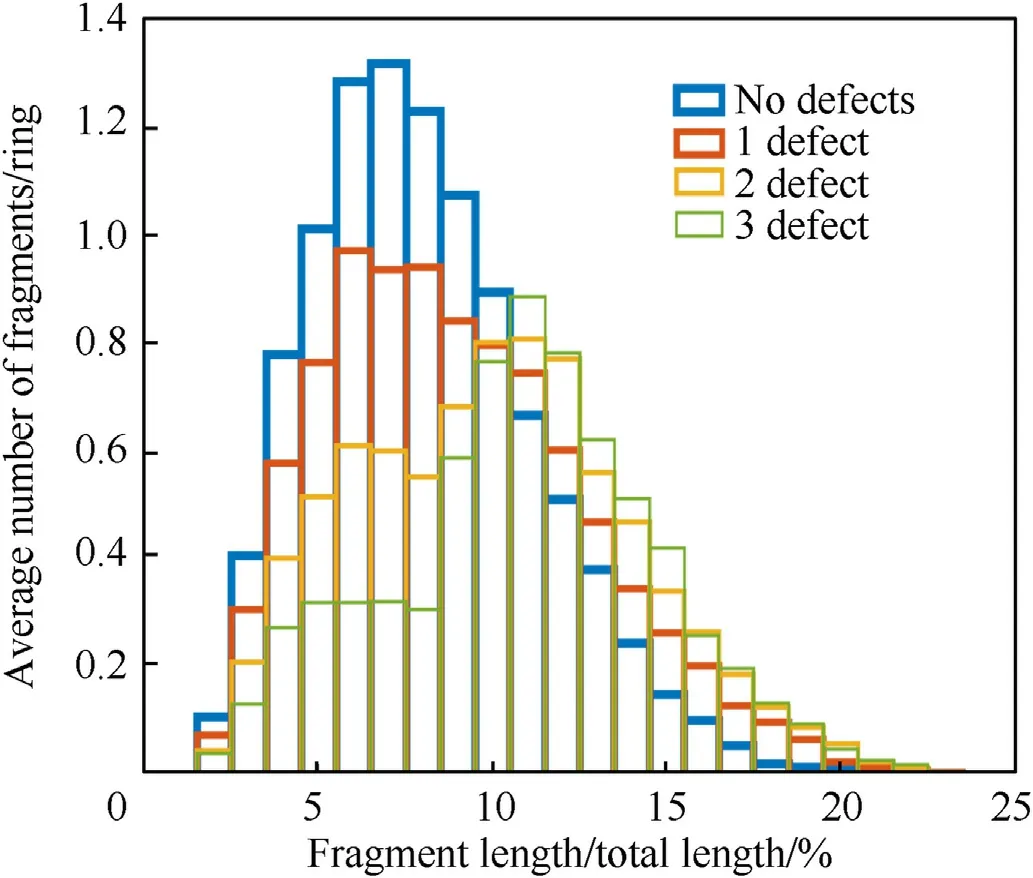
Fig.6.Predicted FSD for 1,2,or 3 initial defects.See text for further details.

Whether a significant defect (that produces a large local reduction in fracture strain) leads to a bimodal distribution also depends on the random scatter in the fracture strains.For example,Fig.7 compares two single defect simulations,one with a 0.1 variation and one where this variation is reduced by an order of magnitude (to 0.01).As expected,the smaller variation leads to a tighter FSD,but importantly it also leads to a more strongly bimodal distribution when an initial defect (low fracture strain element) is present.This effect is also found for an increased number of defects.

Fig.7.The effect of random scatter in the fracture strain on the FSD when a large preexisting defect is present.

The effect of random scatter in the fracture strain on the FSD when a large pre-existing defect is present.

The effect of random scatter in the fracture strain on the FSD when a large pre-existing defect is present.

[scatter_effect].

Finally,the effect of a cyclic variation in properties around the circumference of the cylinder is explored.Although the precise form of the variation simulated here(a sine wave)is not expected in a practical situation,this simulation represents a scenario where there is a long range and progressive variation in the fracture strain with position.Superimposed on this cyclic variation is a random variation in fracture strain of up to 0.05,selected from a Weibull distribution (k=12).Models in which both one and two wavelengths of long range fracture strain variation were compared with the same case with no long range variation.In each case,1000 simulations were again run to produce a converged FSD.An example of the fracture strain distribution for one simulation run of each of these three scenarios is shown in Fig.8(a).Similar to the defect case already explored,the introduction of a long range progressive change in the strain to fracture leads to a broadening of the FSD and also the emergence of a bimodal character to the distribution.In the“2 wave”case,the largest fragments are up to 25%of the circumference length (⋍10 cm for the ring diameter used here).

Fig.8.(a) Example of the fracture strains input to the model to investigate the effect of a cyclic variation.(b) Resulting FSDs for 1000 repeat simulations comparing with and without cyclic variation in fracture strain.

4.Discussion

In this paper,a simple 1-dimensional finite element implementation of the classic Mott fragmentation model for expansion of a thin walled ring has been developed and applied to explore the effect of changing the distribution in fracture strains.An advantage of the finite element implementation is that it enables local variations in fracture strain to be imposed,which is more realistic when considering failure initiated at local inhomogeneities or defects.The model applies to the conditions considered by Mott,namely a ring sufficiently thin so it is reasonable to ignore the interaction between fractures.In such cases,the Mott model has been demonstrated to give good agreement to the observed fragment size distribution across a wide range of metals [2].

An important conclusion drawn by Mott is that the fragment size distribution (normalized by the total ring circumference,as presented in this paper)is controlled by the scatter in the fracture strains and not the fracture strains themselves.Therefore,even if there is a large difference in the strain to failure,providing the scatter in strains-to-failure are similar,the fragment size distribution will be similar.A detailed discussion of FSD and length scales is given by Grady [19].Experiments show that the form of distribution characterized by Fig.2(the“Mott distribution”)is seen in many different alloys,albeit with a difference in scaling.

The choice of distribution of strains to failure has an effect on the predicted FSD,but as demonstrated here,even quite large differences in this choice has only a modest effect on the FSD.Indeed,although full-field FE simulations demonstrate that the number of fragments and FSD does depend on material constitutive properties,it is noteworthy that for even large differences in behaviour(e.g.a very weak 1xxx aluminium alloy compared to a high strength steel)the total number of fragments at a given strain rate is within a factor 2.This is a much smaller difference than the order of magnitude increase in the number of fragments when strain rate is increased [4].This difference in sensitivity is captured in the Mott model presented here.A higher strain rate leads to a larger number of smaller fragments since the time for relaxation (and hence the proportion of the ring that is relaxed)before the next fracture point is activated(fails)is reduced,and hence more fracture points can be activated.

More complex distributions that deviate from Mott were produced by the present model,but only when the variation in position dependent strain to failure was large.Such a situation may arise in the case of a large defect such as a pore or brittle intermetallic particle.In practice,inspection in manufacture is usually performed to avoid occurrence of such large defects.Wrought manufacturing routes (e.g.forging,extrusion,rolling) also help to reduce large defects by mechanically breaking them up or closing them (in the case of pores or cracks).Typically,in a well produced and controlled case,the strain to failure variation is within 1%for a metal [1].However,recent manufacturing innovations,such as additive manufacturing do not benefit from this mechanical working effect and large defects or collections of closely spaced defects are thus occasionally possible [17].

As the present model shows,for large variations in local fracture strain,either due to single isolated defects or gradual variation around the circumference of the ring,a bimodal FSD will be produced.Bimodal FSDs have been observed in practice in some cases[2]although these are usually attributed to distinct fracture mechanisms and fracture intersections.However,the present work demonstrates that bimodal distributions are also to be expected if there are a small number of defects that locally produce a large reduction in the fracture strain.The fragments in the upper peak(larger fragments)are due to the earliest fractures that occur in the elements with lowest fracture strain.As the time between first fracture at defects and initiation of later fracture in the defect-free ring is increased,the time for the growth of the relaxation zone around first fracture sites increases.Since no further fracture can occur in these relaxed regions,they end up becoming the largest fragments.The lower peak(smaller fragments)corresponds to the fragments formed in the defect-free ring,at which point small increments in strain lead to an increased rate of fracture and hence smaller fragment size.

As demonstrated here,whether a bimodal distribution will emerge with the introduction of local flaws depends not only on the reduction in fracture strain at the flaw,but also the random fluctuation in fracture strain at all other positions.For example,if the fluctuations in fracture strain are small,the fragment size distribution is tighter (without a flaw) and thus the introduction of the flaw leads more readily to a bimodal FSD.

Finally,it is noted that the Mott model used as the basis of the work here is obviously an oversimplification of the fragmentation process seen in reality,especially in the case of thicker walled rings,tubes,or plates where the interaction between fractures becomes important [8].For thin walled rings,the Mott model has been demonstrated to work well in predicting the FSD [2].The present implementation of this model has the advantage of running very rapidly(1000 repeats can be completed in seconds)and can be used to explore the effect of variation in initial material flaws orders of magnitude more quickly than a more physically realistic finite element model.The failure model used in the present study is also very simple,and in practice other constitutive parameters such as the strain hardening rate of the material may have an influence[4].In principle,more sophisticated hardening and failure models could be included in the current framework.This is not considered worthwhile given the approximations elsewhere and the objective of a simple,very rapid simulation to screen for interesting conditions for more in-depth evaluation.This more physically rigorous,but time-consuming modelling of selected cases is the subject of ongoing work.

5.Conclusions

A simple model for high strain rate fragmentation of metals has been developed based on a 1-dimensional finite element implementation of the classic Mott method for thin walled rings.The model allows different elements to be assigned locally different behaviour (e.g.fracture strain) representing,for example,the presence of pre-existing flaws.The model has been applied to explore the effect of different assumptions about the distribution of fracture strains.The following conclusions may be drawn from this work:

(1) The fragment size distribution (FSD) produced by the finite element Mott model developed in this work matches well to previous analytical and numerical implementations of Mott,but without the need to pre-assign the locations at which fractures will occur.

(2) The model demonstrates that the choice of function used to assign fracture strains to each element does not have a very large effect on the predicted FSD.The range of fracture strains and the imposed conditions (e.g.strain rate) are far more important parameters.

(3) Non-Mott distributions that can become bimodal are predicted for cases where there are a small number of regions with greatly reduced fracture strain(simulating the presence of a large flaw) or where there is a large but more gradual change in the fracture strain with circumferential position around the ring.

(4) The present model allows the variation in fracture strain distribution and initial flaws to be rapidly explored,identifying interesting cases for more faithful fragmentation modelling.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

The author thanks DSTL and the UK Royal Academy of Engineering for support for this work through the DSTL/RAEng Chair in Alloys for Extreme Environments.The EPSRC are thanked for funding through the LightForm program grant EP/R001715/1 Thanks also to Joe Cordell(DSTL)for valuable discussions relating to fragmentation.The code and data used to create this paper are available on the LightForm Zenodo repository.