量子纠缠、贝尔不等式和量子信息科学到底是什么
2023-05-30周思益
周思益
2022年诺贝尔物理学奖颁给了阿斯佩(A. Aspect)、克劳泽(J. F. Clauser)和蔡林格(A. Zeilinger)这三位科学家,以表彰他们“进行了纠缠光子的实验,确认贝尔不等式不成立,并开创了量子信息科学”。
量子纠缠
要理解量子纠缠的概念,先要从量子说起。量子并不是具体的粒子,而是事物最小的不可分割的基本单元。比如光是由光子组成的,我们可以把一个光子看作一个量子。同样地,一個电子也可以看作一个量子。这次诺贝尔奖的工作是关于纠缠光子的,我们就以光子为例进行说明。光是电磁波,所以光具有偏振性。电磁波的产生机理是变化的电场产生磁场,变化的磁场产生电场。电场和磁场的振动方向互相垂直,并且与电磁波的传播方向也分别垂直。
自然光没有偏振性,它的偏振方向朝向四面八方,大小相等、分布均匀。但当自然光通过竖直的狭缝时,只有在竖直方向振动的光穿过狭缝留了下来,结果原来看起来没有偏振性的自然光就成了在竖直方向有偏振的光。



如何制备这样一对处于纠缠态的光子呢?一般来说,可以使用自发参量下转换的方法。这个方法最早由伯纳姆(D. Burnham)和温伯格(D. Weinberg)提出,随后艾利(C. Alley)和史砚华利用这个方法首次制造出纠缠态。这个方法是把一束光打到非线性晶体上,如偏硼酸钡晶体或磷酸二氢钾晶体,从而将一个光子分为一对互相纠缠的光子。
贝尔不等式
现在一个有争议的问题是Alice和Bob拿到的光子的状态,是测量之前就定好了,还是测量那一瞬间才定好的?这个问题让早期的量子力学专家都非常困惑。爱因斯坦、波多尔斯基(B. Podolsky)和罗森(N. Rosen)认为这些粒子的状态应该是测量之前就定好了。他们三人在1935年发表的一篇名为《能认为量子力学对物理实在的描述是完全的吗?》(Can Quantum Mechanics Description of Physical Reality be Considered Complete?)的论文中设计了一个思想实验,也叫作EPR思想实验或 EPR佯谬[1]。EPR佯谬建立在一个貌似合理的假设——定域论与实在论(合称定域实在论)的基础上。定域论是指某区域发生的事件只能以不超过光速的速度来影响另一个区域的事件;实在论是指实验观测到的现象是某种物理实在,与测量无关。而站在量子力学这一边的玻尔(N. Bohr)认为,这些粒子的状态是测量的时候才突然被决定的。这一争论让人们困惑了很久。
终于,一位叫贝尔(J. S. Bell)的物理学家在1964年提出了一个思想实验——贝尔不等式。如果贝尔不等式不成立,说明量子力学是正确的;如果贝尔不等式成立,则说明经典物理是正确的。贝尔起初是想证明爱因斯坦是对的。原始的贝尔不等式不容易在实验上实现。所以后来这个不等式又有了很多变体,比如CHSH(Clauser, Horne, Shimony, Holt)不等式,CHSH不等式相对容易在实验上实现。具体思路是这样的。
经典物理的结果符合CHSH不等式
假设有两个光子,一个分给Alice,另一个分给Bob。Alice可以用X, Y两种方法对自己的光子进行测量,Bob可以用P, M两种方法对自己的光子进行测量。其中X,Y,P,M代表不同的测量方向。每种方法都有+1或者-1两种可能的取值。令Alice和Bob相距足够远,同时对各自的光子进行测量,并且使用哪种测量方法完全随机。
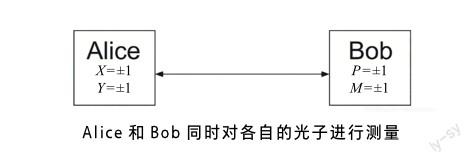


这次诺奖主要是颁发给用实验验证贝尔不等式的工作。
1972年,克劳泽与学生第一次用实验验证贝尔不等式。具体做法是用光照射钙原子,使钙原子发射出一堆纠缠光子。之后在两个地点放置偏振片同时测量光子的偏振,根据光子偏振的统计信息来判断其是否符合贝尔不等式[2,3]。
克劳泽的实验存在漏洞,该实验产生和捕获光子的效率较低,而且偏振片被预先设置在固定的角度,此外,两地的距离不够远,因此这两个地点的光子还有可能存在关联。为了弥补上述漏洞,1981和1982年,阿斯佩及合作者进行了一系列实验。实验中用了一种新方法激发原子,此外,还让两地偏振片的角度自由切换,从而让这两个地点的光子不可能有任何关联。
阿斯佩的实验也有个漏洞,那就是这两个地点的偏振片角度的切换也许并不是随机的,需要产生真的随机数才能堵上这个漏洞。1998年,为了产生真随机数,蔡林格用了两种办法。一种办法现在被称为维也纳屋顶实验,这个实验的做法是在维也纳的两个屋顶上搜集类星体的星光,根据星光的波长来产生随机数。如果波长小于700纳米,则返回1,如果星光的波长大于700纳米,则返回0。由此可以产生真随机数。这样做的原因是:如果使用非常早期的宇宙产生的星光,那么这些星光之间的距离非常遥远,互相不可能有联系。另一个产生随机数的实验是大贝尔实验。这个实验是让几万人注册一个游戏,在游戏中随机点击0或1。也就是说,用人作为随机数生成器。如果你相信自由意志的话,几万人随机点击的0和1就应该是真的随机数。蔡林格利用人的自由意志产生的随机数进行贝尔不等式的实验,堵住了最后一个漏洞[4,5]。
量子纠缠的其他应用
量子隐形传态
蔡林格的另一个贡献是他在1997年做的量子隐形传态实验[6]。量子隐形传态简单来说就是把一个粒子包含的所有的量子信息传到另一个粒子上。虽然测量一个粒子的所有量子信息是不可能的(因为一个粒子包含的量子信息有很多种,一旦进行测量,得到一部分量子信息的同时也就会失去另外的量子信息),但是有可能把一个粒子的量子态完全传送到另一个粒子上,当然,原本粒子的量子态也就被破坏了。
量子纠缠交换

利用量子隐形传态的技术,可以把两个从来没有接触过的粒子变成纠缠态。考虑这样一个实验:最初1和2、3和4分别是纠缠态。现在让2和3变成纠缠态,那么1和4也就变成纠缠态。这样一来1和4这两个从未接触过的粒子之间就产生了纠缠。蔡林格的实验组于1998年首次在实验上展示了量子纠缠交换。光子在光纤中传播的距离是有限的,如果光纤太长会使得光子被吸收或特性被损失,而利用量子纠缠交换技术就能极大提高一对互相纠缠的光子沿着相反方向传播的距离。
量子信息科学
这次获奖的实验工作为量子信息科学奠定了基础。量子信息科学是量子力学和信息科学形成的一个交叉学科,分为量子通信、量子计算和量子精密测量三大研究方向。其中,量子通信主要包括量子隐形传态和量子密钥分发;量子计算包括了量子因数分解和量子搜索;量子精密测量包括了原子钟、原子雷达等。
量子信息科学以量子力学的基本原理作为基础,涉及量子叠加和量子纠缠。量子信息科学就是利用量子力学的这些特性进行计算编码和信息传输。在经典计算机里,储存信息的基本单元是0、1这样的经典比特,经典计算机的芯片元件会达到极限尺度。在量子信息科学里,使用|0〉和|1〉的叠加态作为量子比特,构成储存信息的基本单元。对于具有n个量子比特的体系,其本征态有2n个,任意一个态可以表示为这些本征态的叠加。虽然量子计算机有这样大的优势,但目前只是在少数问题上比经典计算机更为优越,例如因数分解和无结构数据库搜索。
量子通信方面,“墨子号”卫星的发射,标志着我国的量子信息技术达到世界领先水平;量子计算方面,“九章”标志着我国的量子计算水平实现量子计算优越性;量子精密测量方面,具有超高灵敏度核自旋磁传感器标志着我国的量子精密测量技术在世界领先。我们有理由相信,在不远的将来,我国的量子信息科学一定会取得更优异的成绩!
[1]Einstein A, Podolsky B, Rosen N. Can quantum mechanics description of physical reality be considered complete? Physical Review, 1935, 47: 777-780.
[2]Clauser J F, Horne M A, Shimony A, et al. Proposed experiment to test local hidden-variable theories, Physical Review Letters, 1969, 23: 880-884.
[3]Clauser J F, Horne M A, Experimental consequences of objective local theories, Physical Review D, 1974, 10: 526-535.
[4]Aspect A, Grangier P, Roger G. Experimental tests of realistic local theories via Bells theorem. Physical Review Letters, 1981, 47: 460-463.
[5]Aspect A, Grangier P, Roger G. Experimental realization of Einstein-Podolsky-Rosen-Bohm gedankenexperiment: A new violation of Bells inequalities. Physical Review Letters, 1982, 49: 91-94.
[6]Bouwmeester D, Pan J W, Mattle K M, et al. Experimental quantum teleportation. Nature, 1997: 390: 575-579.
關键词:量子纠缠 贝尔不等式 量子信息科学 ■
