系统级电磁敏感性综合评估模型研究
2023-05-30宫峰勋孙健
宫峰勋,孙健
(中国民航大学电子信息与自动化学院,天津 300300)
随着民用航空信息化的发展,机场内的电子设备日益增多,各种设备之间产生电磁干扰的可能性也会增加。电磁敏感性(EMS,electromagnetic susceptibility)是电子器件或设备对周围电磁干扰耐受能力的一种定量度量。电子系统由多个电子器件或设备组成,容易受到周围电磁干扰的影响。为此,需要建立一种模型来表征电子系统对电磁干扰的敏感性,从而评估电子系统的抗干扰能力。系统级EMS 的研究具有较强的应用背景,如在特定环境中安装某电子系统,需要测量环境中可能存在的电磁干扰,并分析在当前电磁环境下,系统是否能正常工作,系统失效概率多大以及可能在何时失效。
在相关文献中,对EMS 的研究主要聚焦在干扰阈值的分析上。干扰阈值分析一般采用实物测试和模型预测两种方法。多个国家在国际电工委员会的EMS 标准下制定了相应的EMS 测试规范和执行标准。Cheaito等[1]建立了基于大电流注入测试的敏感性模型,且通过改变调谐参数的方法克服了特定系统只能套用特定EMS 测试模型的缺陷,该模型预测方法具有普适性和消耗成本低的优点,但其精确度与实物测试结果有一定偏差。Park等[2]提出一种基于谐波平衡法进行非线性电路分析的数值技术,但其不适用于复杂系统分析。Martorell等[3]提出使用反射功率进行射频接收机前端三阶互调的EMS 计算,结果与标准估计值较吻合,但该方法只讨论了非线性导致的互调敏感性。Yan等[4]通过Volterra 级数进行接收机频响特性的分析,但该模型缺乏明确的描述参数,只是根据敏感性条件得到了干扰阈值曲线。Song等[5]使用神经网络进行EMS 快速预测,但该方法训练耗时长且需要大量数据支撑。
综上,上述模型不够直观全面,用户更加关心系统在当前环境下能否正常工作。针对上述问题,结合信号完好性的研究方法[6-10],提出描述系统级EMS 的综合评估模型,模型包含误差阈值、系统失效概率和告警时间3 个参数,分别定义如下:
(1)误差阈值,干扰信号造成系统性能指标产生的误差,以及对应干扰信号强度的阈值;
(2)系统失效概率,在当前误差阈值下,系统丧失正常工作能力的概率;
(3)告警时间,系统出现功能失效到用户接收到告警的时间。
1 误差阈值建模原理
为了便于在评估后找到不满足EMS 标准的功能模块,采用模块化的分析方法,即将整个系统分解为多个功能模块,然后按照模块是否为线性系统分别求解各个功能模块的EMS 误差阈值。以超外差接收机为例,功能模块划分如图1 所示。
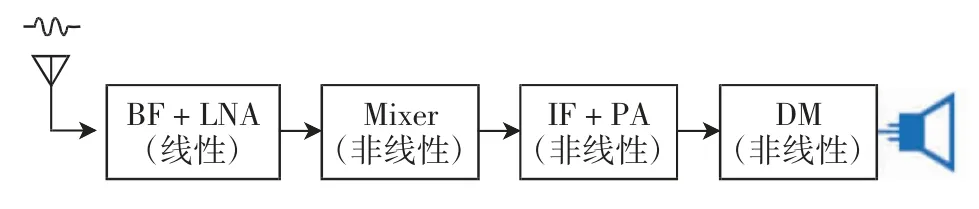
图1 超外差接收机的功能模块组成Fig.1 Composition of functional module of superheterodyne receiver
为了模型建立的简便性,将滤波器和放大器整合为一个模块,称为滤波放大模块。图1 中模块依次为高频滤波放大模块(带通滤波器(BF)和低噪声放大器(LNA))、混频模块(Mixer)、中频滤波放大模块(中频滤波器(IF)和功率放大器(PA))以及解调模块(DM),包括1 个线性模块和3 个非线性模块。
图2 为功能模块输入与输出关系。EMS 误差求解的基本关系式为

图2 功能模块的输入与输出关系Fig.2 Relationship of input and output of functional module
式中:y(t)和y′(t)表示对应的输出信号;H[]表示功能模块的输入与输出关系;s(t)和s′(t)表示两种不同的输入信号。
理论上,如果要分析模块的EMS,首先要分析伴随干扰信号输入情况下与只输入有用信号时线性模块输出信号之间的偏差。但对于用户来说,分析干扰导致输出信号产生的误差并不能直观地表示当前模块性能的劣化程度,也不能说明其工作状态,因此为了获得更直观的误差阈值指标,让用户可以直接了解在某种信号环境下模块是否能达到输出端要求的最低性能,考虑通过建立输入端评估指标与输出端正常工作最低要求的映射关系模型,并将误差阈值指标与输入干扰信号联系起来。误差阈值包括增益、灵敏度和抗干扰裕量3 个指标:增益误差阈值指模块可承受的最大干扰造成的有用信号增益下降的最大值;灵敏度误差阈值指模块可承受的最大干扰造成的灵敏度下降的最大值;抗干扰裕量(AJM,anti-jamming margin)误差阈值为实际输入有用信号与存在干扰时灵敏度的比值,在信号和干扰一定的情况下,抗干扰裕量反映了模块对干扰的容忍能力,所以抗干扰裕量误差阈值指模块可承受的最大干扰造成的抗干扰裕量下降的最大值。
根据上述误差阈值指标可以定量描述干扰对评估指标的影响,实际应用中还要满足一系列限制条件以达到输出端最低性能的要求。以此条件为最低标准,可以求解评估指标的阈值和对应的输入干扰信号阈值,称这个限制条件为EMS 判据,如下
式中No为噪声功率。即存在干扰时,为了保证输出端性能,首先要保证实际输出信号So不小于最小输出有用信号S′o,min,否则可能丢失有用信息;其次实际输出干扰信号Io不能超过最小输出有用信号S′o,min,否则会淹没有用信号;最后要保证输出端信干噪比(SINR,signal to interference plus noise ratio)不小于输出端信干噪比门限值SINRo,min。
上述3 个误差阈值指标不满足任意一个,模块将无法正常工作,因此,通过3 个指标求解EMS 可以获得三者中最敏感的误差阈值和对应的干扰信号阈值。
1.1 线性模块EMS 误差阈值
对高频滤波放大模块“BF+LNA”进行EMS 误差阈值分析。
1)线性模块增益误差阈值指标
由于线性模块满足齐次性和叠加性,所以对干扰信号的作用与有用信号等效,二者互不干扰,干扰并不会影响有用信号的增益,也就不会存在增益误差。
2)线性模块灵敏度误差阈值指标
灵敏度是受到模块输出端信干噪比SINRo=So/(No+Io)约束的,则输入有用信号功率表示为
式中GP为功率增益。
根据噪声系数的定义,有
式中:NPi为当前模块的输入噪声;k=1.38×1023J/k,为玻尔兹曼常数;Tpm为前一级模块的噪声温度,等效为290 K;Bn为模块工作带宽。
将式(4)中No代入式(3),整理得输入信号功率为
若最小信干噪比为SINRo,min,则干扰条件下的降级灵敏度表示为
灵敏度误差为
3)线性模块抗干扰裕量误差阈值指标
降级抗干扰裕量可表示为
抗干扰裕量误差为
模型仿真:设该模块的中心频率为1 090 MHz,模块工作带宽Bn=6MHz,输入有用信号功率Si=-85dBm。在上述条件下,最小信干噪比门限值SINRo,min分别为0、5、10 dB时,得到线性模块的灵敏度误差阈值曲线如图3 所示,抗干扰裕量误差EMS 曲线如图4 所示。
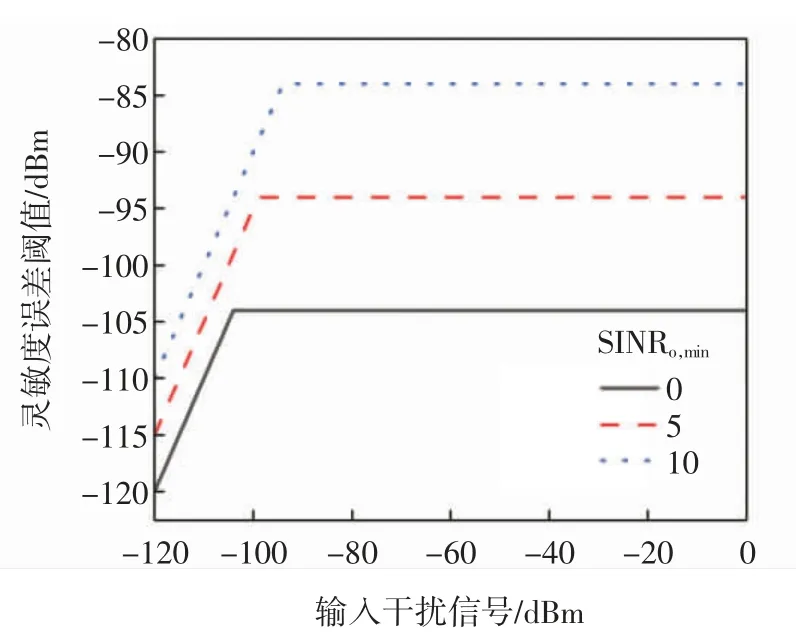
图3 线性模块的灵敏度误差阈值曲线Fig.3 Sensitivity error threshold curve of linear module
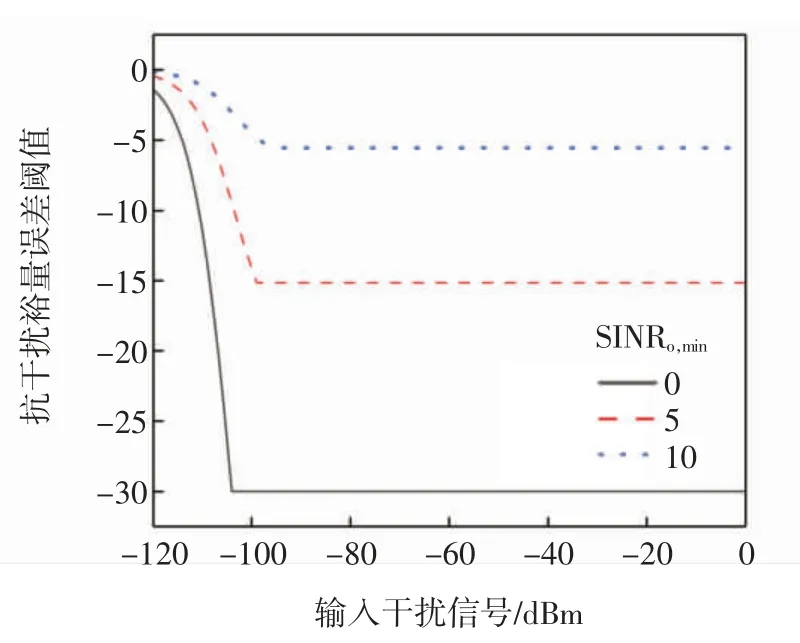
图4 线性模块的抗干扰裕量误差阈值曲线Fig.4 Anti-jamming margin error threshold curve of linear module
图3中,随着输入干扰信号的增大,灵敏度误差ΔSi,min逐渐增大,说明在受到干扰后,灵敏度下降,不同信干噪比标准下的灵敏度误差阈值不同。当SINRo,min=0 dB时,灵敏度误差阈值ΔSi,min=-104 dBm,这个值是当前状态下线性模块可容忍的灵敏度最大误差,对应的干扰功率阈值Ii,max=-104.8 dB。超过这个误差阈值模块性能会下降,图3 中只讨论模块所能承受输入干扰信号的阈值对应评估指标的阈值,由于该研究只分析阈值求解,阈值之后的分析对于该模型意义不大,此后用垂直于横轴的直线代替。
图4中,抗干扰裕量误差ΔAJM <0 且随着干扰增大而减小,说明干扰条件下的抗干扰裕量AJM′小于无干扰时的抗干扰裕量AJM,进一步说明模块对干扰的容忍能力变差。当干扰达到一定强度时,抗干扰裕量误差达到最大,表明此时模块对干扰强度的容忍能力已经达到极限。当SINRo,min=0 dB时,模块能容忍的抗干扰裕量误差阈值ΔAJM=-29.976 3,对应的干扰信号功率阈值Ii,max=-104.5 dBm。
1.2 非线性模块EMS 误差阈值
非线性模块的输入输出关系比较复杂,不能使用线性模块的分析方法,一般使用级数进行分析。考虑一般情况,使用以下幂级数来描述非线性模块的输入输出关系
式中ai(i=1,2,…,n)为非线性特征系数。假设输入信号为s′(t)=s(t)+i(t)=VSicos ωSt+VIicos ωIt,则输出信号为
分析式(11),输入为双音信号,但输出却出现了很多分量。输出信号与干扰信号的频率、幅度以及非线性模块的特征系数有关。
对超外差接收机中非线性模块的误差阈值分析如下。
1)非线性模块增益误差阈值指标
无干扰时,非线性模块的功率增益表示为
有干扰时,非线性模块的功率增益表示为
则功率增益误差表示为
2)非线性模块灵敏度误差阈值指标
无干扰时,非线性模块的灵敏度表示为
式中SNRo,min为信噪比。有干扰时,非线性模块的降级灵敏度表示为
则接收机非线性模块的灵敏度误差EMS 模型为
此外,由于输入不同频率的干扰信号与输出到带内的组合干扰存在不确定关系,不同频率的干扰对灵敏度造成的影响不同,根据这种差异性,通过控制干扰信号功率不变,求解不同频率干扰信号对灵敏度造成的误差。
3)非线性模块抗干扰裕量误差阈值指标
无干扰时,非线性模块的抗干扰裕量表示为
有干扰时,降级抗干扰裕量表示为
则抗干扰裕量误差为
模型仿真:设该模块的中心频率为1 090 MHz,工作带宽Bn=6 MHz,输入有用信号功率Si=-85 dBm,非线性特征系数a1=12.6,a2=5,a3=-3。
在上述条件下,非线性模块的灵敏度误差阈值随干扰信号功率变化的曲线如图5 所示。
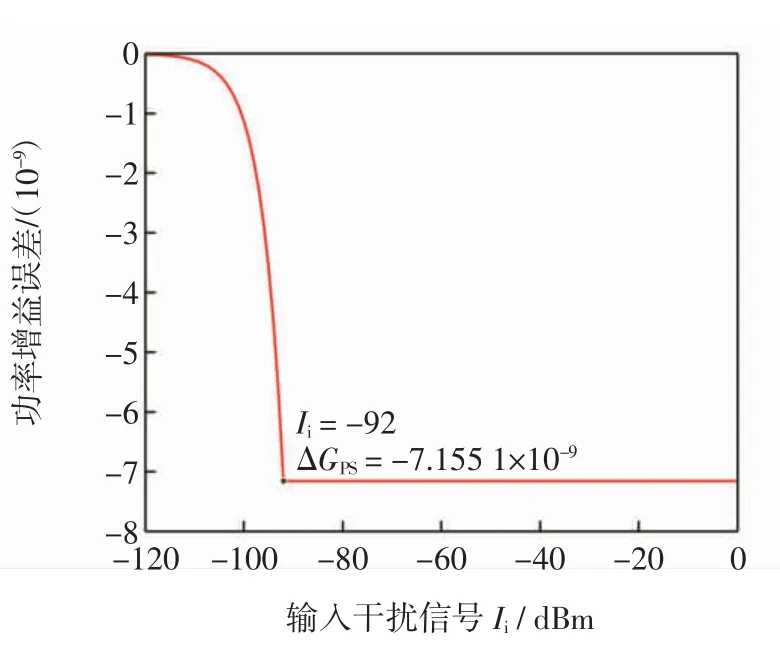
图5 非线性模块的增益误差阈值曲线Fig.5 The gain error threshold curve of the nonlinear module
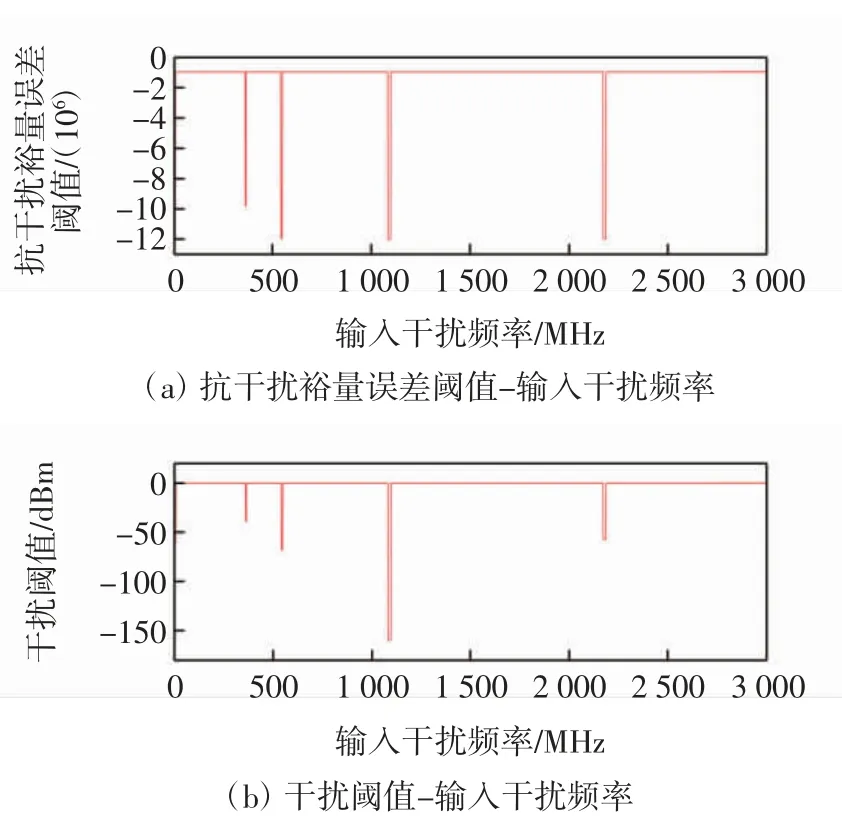
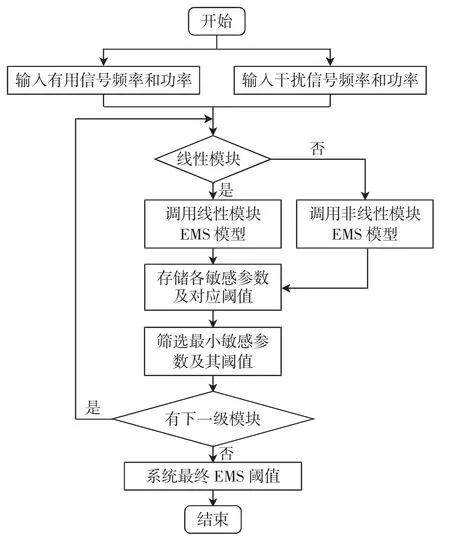
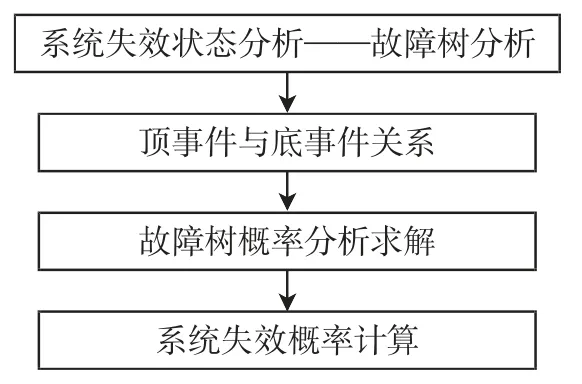
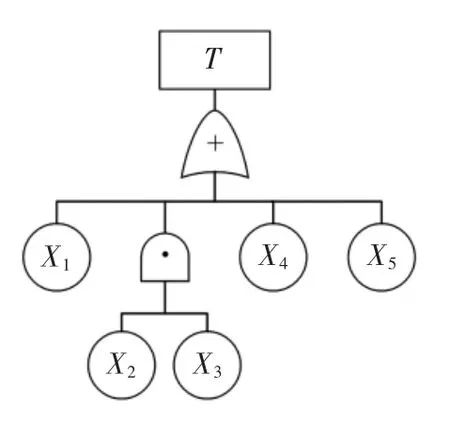
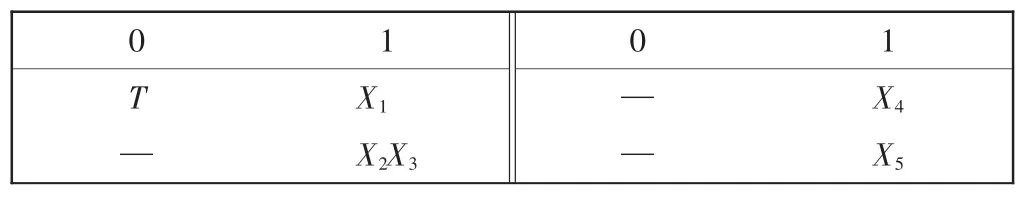
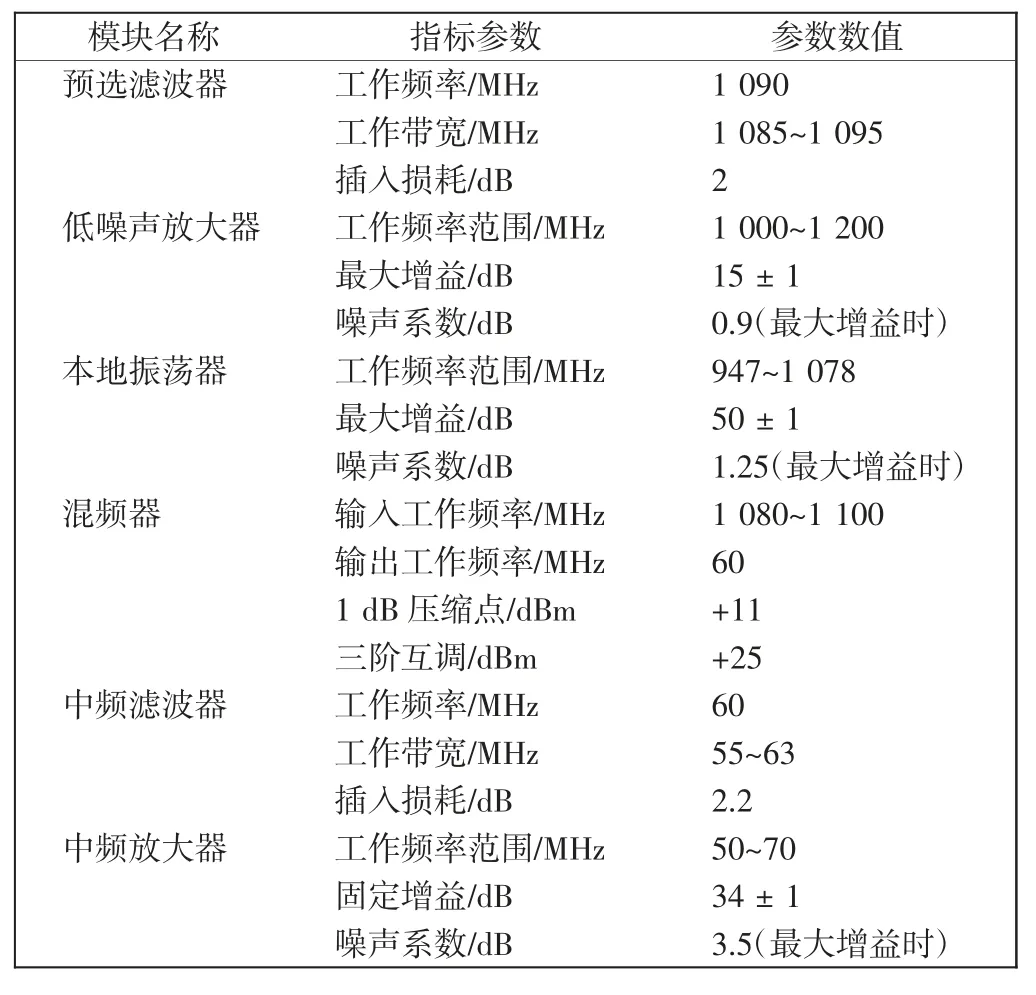
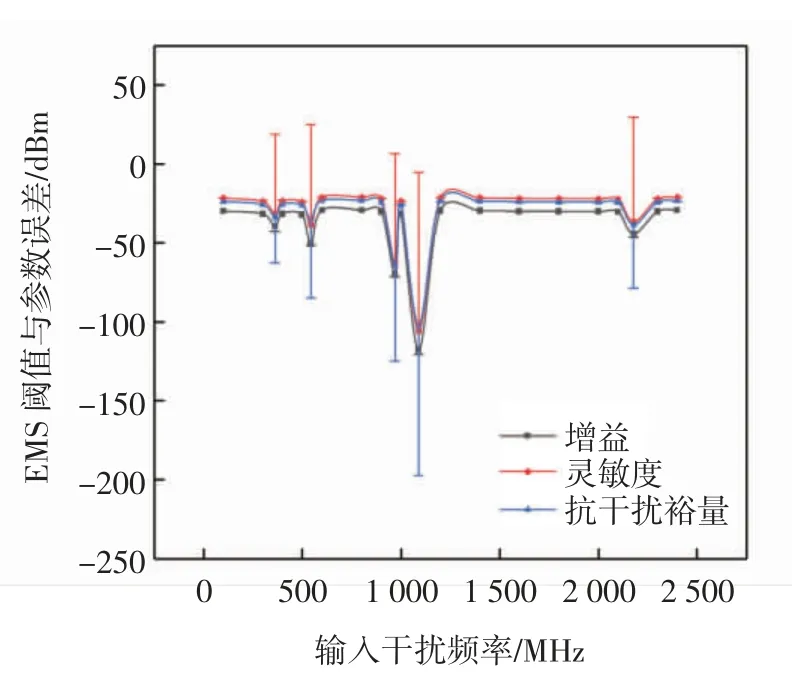
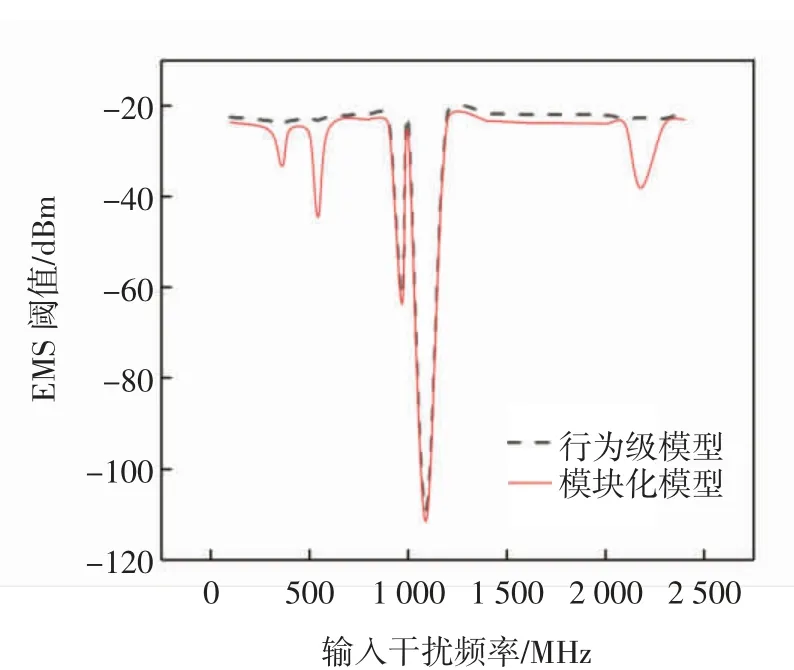
图5中,有用信号功率增益误差ΔGPS<0,说明干扰存在时G′PS 在图5 的条件下,改变干扰信号频率,在1 Hz~3 GHz 频段内进行扫频,得到该干扰频段的灵敏度误差阈值和干扰阈值曲线,结果如图6 所示。 图6 非线性模块的灵敏度误差阈值曲线Fig.6 Sensitivity error threshold curve of nonlinear module 图6 中非线性模块在不同干扰信号频率的情况下,敏感性阈值是不同的,对中心频率附近的带内干扰是最敏感的,当干扰达到-158 dBm时,模块的输出性能就已经不再符合性能要求;对于带外的干扰如频率为545 MHz时,干扰功率需要达到-67 dBm 才能对模块造成性能损失。 图5 条件下,抗干扰裕量误差阈值和干扰阈值曲线如图7 所示。 图7 非线性模块的抗干扰裕量误差阈值曲线Fig.7 Anti-jamming margin error threshold curve of nonlinear module 图7 中非线性模块的抗干扰裕量误差为ΔAJMN<0,抗干扰能力变弱,同灵敏度误差相似,但不同频段阈值也有所不同。 对模块的EMS 误差阈值模型进行整合,从而形成整个系统的EMS 模型。整合的原理是各模块之间有着“此输出为彼输入”的关系,即任意模块的输入都是前一级模块的输出,且各模块敏感性阈值服从“短板效应”,即阈值最小的敏感参数决定模块最终的干扰阈值。这样就将各模块的模型联系起来,形成完整的系统级求解模型,如图8 所示。 图8 系统级EMS 模型的求解方法Fig.8 Solving method of system-level EMS model 图8中,当前模块为线性模块时,即调用线性模块的EMS 模型,否则调用非线性模块的EMS 模型;求解到最后一个模块时,整个系统的EMS 分析结束,输出最终结果。 当外界存在干扰信号时,系统的某个或多个功能模块有可能会不正常工作,可能会造成系统功能失效。根据国标GB7829-87,故障树分析(FTA,fault tree analysis)适用于系统失效概率的分析[11-13],采用布尔逻辑组合低阶事件,利用演绎式的失效分析方式建立系统中特定组件的失效率与系统失效率之间的关系,在模块化分析方式下,非常适合使用故障树对系统进行失效概率的推导分析。 设系统有N 种存在状态,Pω为失效状态概率,为了求解具有一般性,计算系统多次工作后累积失效概率,求解均值概率作为最终结果。M 为导致系统失效的工作次数,则系统失效概率的计算公式为 设计完成的系统失效概率的具体计算流程如图9所示。利用故障树分析法,绘制的系统故障树如图10所示。 图9 系统失效概率计算流程Fig.9 Calculation process of system failure probability 图10 系统故障树Fig.10 System fault tree 系统中每个功能模块有两个工作状态(正常或失效),那么系统的工作状态就可以根据模块状态及其组合状态得出。根据第1 节中的超外差系统,有4 个功能模块,由于混频模块Mixer 结构特殊,分解为本振X2和混频X3讨论。 采用图10 中X1,X2,X3,X4和X5这5 个底事件,表示各功能模块的失效状态。利用不交型布尔代数法求解顶事件T 的概率,利用下行法求解故障树的最小割集,如表1 所示。 表1 故障树最小割集Tab.1 Minimum cut set of fault tree 根据最小割集,顶事件由底事件表示为 式(22)中最小割集之间不相交,对其两端求概率,即顶事件发生的概率 顶事件发生的概率即系统失效概率。 由于正态分布和泊松分布过于理想化,底事件模块失效的概率分布可用Weibull 分布来分析,参考文献[14-15],Weibull 分布广泛应用于可靠性和失效分析中,其概率密度函数为 式中:x 是随机变量;λ 是比例参数;q 是形状参数,q<1 时表示失效率随时间减小,q=1 表示失效率是不随时间变化的,代表外部事件引发的失效,q>1 表示失效率随时间增大,这种情况考虑到模块“老化”的问题,分析更复杂。因此,仅考虑q=1 的情况。 系统多次工作的过程可以转化为一个马尔可夫过程,在马尔可夫过程中,系统能以若干独立状态存在。如果系统在第n+1 次工作时失效,那么第n 次为非失效状态,第n 次到第n+1 次即为失效状态转化的概率[16-18]。利用马尔可夫求解累积失效概率,进而求解告警时间的数学期望,是比较符合工程实际的。 设s 为状态向量,令s1表示失效状态,sN表示非完全失效状态,s2~sN-1表示其他状态。s(n)为系统第n 次工作后各状态的累积概率向量,s(0)表示未工作前各状态的概率向量,T 为状态转换矩阵,则第n+1 次工作后各个状态的概率向量为 由于系统未工作前,系统的非失效概率为1,其他状态概率为0,则系统工作前的累积失效概率为0。由于T 的元素Tij表示系统从第i 个状态转换到第j 个状态的概率,则 则系统在第n+1 次工作后的累积失效概率为 令Z 变量为系统失效的次数,令 式中ε 为正无穷小。 假设从干扰导致系统失效到用户收到失效告警的时间为Δt。结合式(21)和式(29)得到告警时间的数学期望为 以某民航多点定位接收机为例进行综合评估分析。表2 提供了各功能模块的参数,表3 提供了被测接收机的整体系统参数,其中,输入有用信号功率Si=-97 dBm,中心频率为1 090 MHz。 表2 多点定位接收机各模块参数Tab.2 Parameters of each module of the multi-point positioning receiver 表3 系统整体性能参数Tab.3 Overall system performance parameters 图11采用误差棒的形式表示误差阈值,从图11中可以看到各个频点干扰作用时对3 个指标造成的误差以及每个参数对应的干扰阈值。通过对比确定该多点定位接收机的增益误差阈值对干扰最敏感,因此选取增益作为该接收机的EMS 曲线。通过与实测数据进行比较,平均误差为3.77 dB,在工程允许范围内。 图11 多点定位接收机EMS 误差阈值曲线Fig.11 EMS error threshold curve of multi-point positioning receiver 以往对于系统级EMS 的预测仿真方法,比较经典的是Yan等[4]提出的接收系统Volterra 行为级模型,主要使用Volterra 级数的三阶简化模型对整机的非线性输出效应做了EMS 分析和总结,对两种模型进行对比实验,结果如图12 所示。 图12 误差阈值模型与Volterra 行为级模型比较Fig.12 Comparison of error threshold model and Volterra behavioral model 图12 中行为级模型对于频带外的一些符合组合干扰条件的干扰并未做进一步的分析,而模块化误差阈值模型在考虑了组合干扰的情况,得到了一个频段内相对完整的EMS 曲线。 根据图9 的计算过程,使用Matlab 随机产生服从Weibull 分布的数据并计算平均失效概率,各模块的失效概率如下:①BF+LNA 模块为0.203;②Mixer 模块为0.265;③IF+PA 模块为0.237;④DM 模块为0.211。 某一次告警时间为7.83 s。利用第2 节和第3 节中的参数模型求解系统失效概率和告警时间,令ε=10-5,进行20 次仿真计算。计算得到实验系统在误差阈值条件下的系统失效概率为91.6%,告警时间的期望值为8.52 s。系统在干扰阈值下失效概率非常大,不仅得到了干扰信号的阈值,也得到了3 个评估指标的误差阈值,另外,从系统失效概率和告警时间两个方面丰富了系统级EMS 的研究内容。通过上述实验进行了模型的仿真和应用,可以达到预期的评估效果,验证了建立综合评估模型思想的正确性以及理论的可行性。 该研究提出综合评估模型来预测和评估系统级EMS,使用误差阈值、系统失效概率和告警时间3 个参数来描述系统级EMS。通过将系统进行模块化、多指标的方式分别对线性和非线性模块进行误差阈值求解;在得到误差阈值的基础上,根据模块化理论和故障树分析方法结合,计算系统失效概率;在系统失效概率的基础上,根据马尔可夫过程推导,得到了告警时间模型,最终得到了综合评估模型的3 个描述参数的数学模型。以民航多点定位接收机为研究对象进行仿真实验,对比经典Volterra 行为级模型,得到了以往EMS 研究中的干扰阈值曲线,并进一步提出和得到了3 个误差阈值曲线。此外,丰富了EMS 的研究内容,得到了系统失效概率和告警时间两个描述参数的估计方法。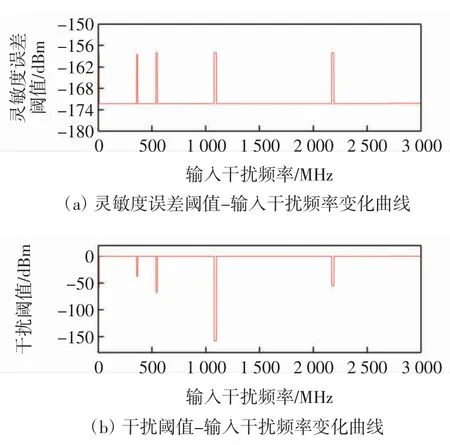
1.3 系统级EMS 误差阈值
2 系统失效概率分析
3 告警时间分析
4 实验仿真分析

5 结语
