从震源破裂过程角度分析中国大陆强震面波震级高于矩震级的原因
2023-05-30许月怡张勇
许月怡 张勇
北京大学学报(自然科学版) 第59卷 第3期 2023年5月
Acta Scientiarum Naturalium Universitatis Pekinensis, Vol. 59, No. 3 (May 2023)
10.13209/j.0479-8023.2023.020
国家自然科学基金(42021003, 42074058)资助
2022–05–24;
2022–06–23
从震源破裂过程角度分析中国大陆强震面波震级高于矩震级的原因
许月怡 张勇†
北京大学地球与空间科学学院, 北京 100871; †通信作者, E-mail: zhang-yong@pku.edu.cn
基于有限断层模型和数值模拟, 研究震源参数对面波震级的影响。结果表明, 在矩震级相同的情况下, 地震破裂持续的时间越短, 面波震级就越高, 反之亦然。影响地震持续时间的震源参数包括子断层破裂持续时间、破裂速度和破裂长度。若地震矩不变, 子断层破裂持续时间和破裂长度与面波震级负相关, 破裂速度与面波震级正相关。中国大陆测定的面波震级多数情况下显著高于矩震级的原因可能有二: 一是中国大陆发生的强震多为板内地震, 由于应力降偏大, 破裂持续时间和断层长度可能偏短; 二是相对于美国国家地震信息中心测定的s(20), 中国地震台网中心测定的面波震级系统性地偏大。
面波震级; 矩震级; 震源参数
面波震级(s)和矩震级(w)是衡量强震(震级>6.0)规模的两种常见标度, 二者各有优缺点。面波震级的测定相对简单, 但当>8.5时, 容易发生饱和; 矩震级不会饱和, 但与地震波能量的关系较弱, 某些情况下无法较好地反映震感和灾害的程度。对一般地震而言, 不同震级标度之间整体上存在线性经验关系[1−3], 但具体到某一个地震事件, 中国地震台网中心(China Earthquake Networks Center, CENC)测定的面波震级(s)、美国国家地震信息中心(National Earthquake Information Center, NEIC)测定的s(20)以及全球矩心矩张量组(Global Centroid- Moment-Tensor, GCMT)测定的矩震级w之间存在较大的差异(图 1)。例如, 2014 年云南景谷地震的s比w大 0.8 级, 2017 年西藏米林地震的s和s(20)比w大 0.4 级(表 1)。
震级测定的一致性问题一直备受关注。矩震级完全取决于地震矩, 与断层附近介质的剪切模量、错动面积和位错量相关, 对断层错动的时间过程不敏感[4]; 面波震级则由面波振幅与周期的比值决定,s和s(20)采用的面波周期范围也有差别[4], 所以受断层错动时间过程影响。一个较为简单且极端的例子是, 假定两次矩震级相同的地震事件具有相同的位错量, 但其中一次事件完成这一错动的时间为10s, 另一次事件完成这一错动的时间为 100s, 由于用于测定面波震级的远场地震波幅度与断层错动速率成正比, 前者的面波幅度显著高于后者, 导致其面波震级明显偏大。
本文基于有限断层模型, 采用不同的震源参数模拟地震波, 并基于模拟的地震波测定其面波震级,详细地探究不同的震源参数(包括子断层破裂(断层上质点振动)持续时间、破裂速度和破裂长度)如何造成面波震级与矩震级的差异。

Ms, Ms(20)和 Mw 分别来源于中国地震台网中心正式目录(http://data. earthquake.cn)、美国国家地震信息中心(https://www.usgs.gov/)和全球矩心矩张量项目(https://www.globalcmt.org/)

表1 2009年1月至2021年12月中国大陆Ms ≥6.5地震目录
1 研究方法
1.1 基于有限断层模型的地震波模拟
根据震源表示定理, 地震辐射的波场可以表示如下[5]:

m(,)=0()(,)(v+v),




中国基式(SK)中长周期地震仪的传递函数[10]为

美国世界标准台网长周期(WWSSN-LP)地震仪的传递函数[11]为

两种仪器的幅频特性曲线(图 2)表明, SK 地震仪对 0.1~15s 周期的地震波响应较好, 其频带在0.2~11s 是平坦的; WWSSN-LP 对 3~50s 周期的地震波反映较好, 频谱峰值出现在 15s[4]。考虑到中国地震台网与境内地震的平均震中距小于 25°, 而s(20)需要震中距大于 20°, 我们分别设定震中距在 5°~25°和 30°~90°范围内均匀分布的各 100 个观测台站来测定s和s(20), 如图 3 所示。

图2 中国基式(SK)中长周期地震仪和世界标准台网长周期(WWSSN-LP)地震仪的幅频特性曲线
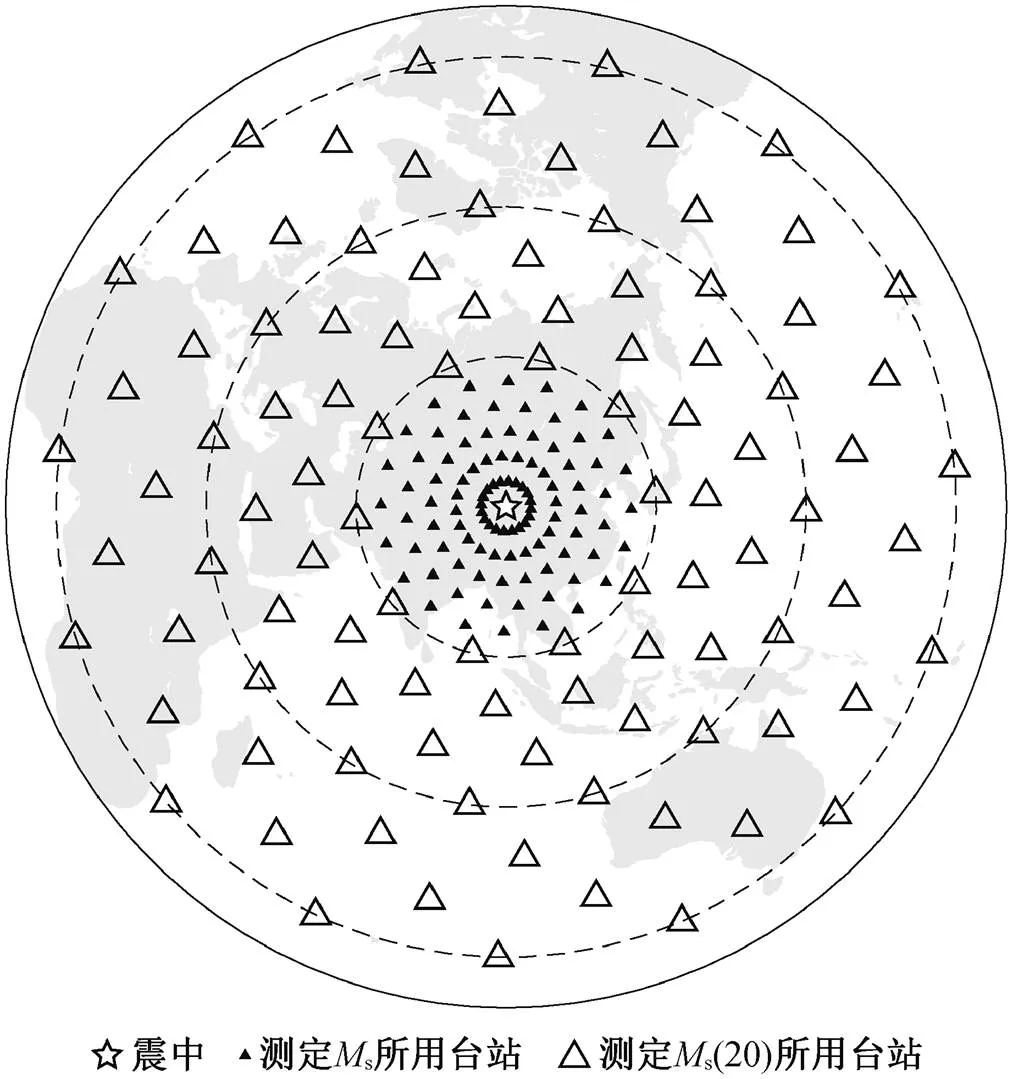
图3 测定Ms和Ms(20)所用台站分布
为了探究矩震级固定情况下震源参数对面波震级的影响, 分别模拟矩震级为 6.8, 7.2 和 7.5 的地震, 包括单侧和双侧破裂模型(即表 2 中 6 种震例), 震源机制固定, 断层的走向、倾角和滑动角分别为 90°, 45°和 45°。图 4 和 5 以w= 7.2 为例, 展示震源参数的定义。破裂长度为, 矩震级为 6.8, 7.2 和 7.5的破裂模型分别采用 1km×1km, 2km×2km 和 3km×3km 的子断层, 震源时间函数均用一个简单的等腰三角形表示, 破裂起始时间用子断层到震源的距离除以破裂速度r来计算, 子断层的破裂持续持续时间为r(图 5(a)), 故整个地震的破裂持续时间为a=max/r+r(max与正相关), 双侧破裂(图5(c))持续时间少于单侧破裂(图 5(b))。以单侧破裂s(20) =w时的震源参数为参照, 6 种模拟震例都在参考模型(表 2)的基础上, 分别改变,r和r, 根据式(2)~(5)合成台站处的地震观测记录, 模拟的观测数据采样率设定为 1 sps。

表2 破裂模型的震源参数

图4 参考模型的断层面滑动分布(Mw =7.2)

(a)子断层震源时间函数示意图; (b)和(c)参考破裂模型的地震矩率函数(Mw =7.2, L=60 km, Vr =3 km/s, 子断层破裂持续时间为10 s)
1.2 震级公式
目前, CENC 测定浅源地震(深度小于 60km)水平向面波震级时, 需要将宽频带数字地震记录仿真为 SK 地震仪的模拟记录, 然后根据下式[10]来计算:
有助于维护南海地区和平稳定。此次海上联演的主要内容之一,是熟悉“海上意外相遇规则”的使用。“海上意外相遇规则”于2014年4月在中国青岛举行的西太平洋海军论坛上通过,旨在减少误解误判,防止发生海上意外事件。2016年9月举行的第十九次中国-东盟领导人会议,审议通过了《中国与东盟国家关于在南海适用〈海上意外相遇规则〉的联合声明》,为中国和东盟国家海军的船舶和航空器在南海意外相遇时的应急处置和操作规范提供了明确指引。通过此次演练,未来中国与东盟海军舰船在南海相遇时,可以利用该规则及时沟通,防止出现误判和意外事件,这有助于维护南海地区和平与稳定。
s=lg(H/H)max+1.66lg()+3.5,
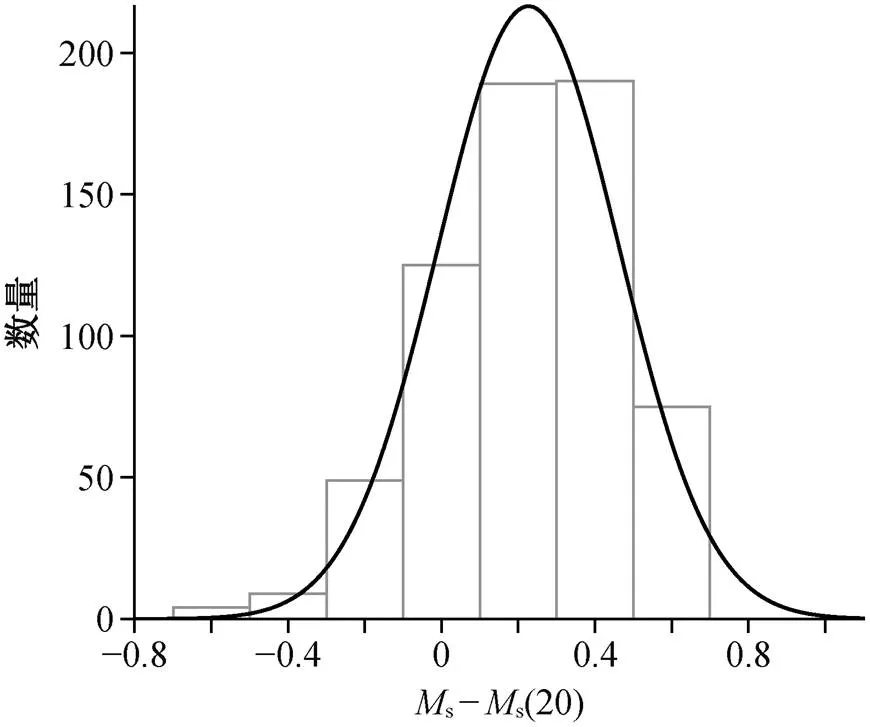
2°<<130°, 3s 式中, (H/H)max代表求取同一时刻或周期相差在1/8 周期之内的两水平分量面波位移的矢量和的模H(单位: μm)除以对应周期H(单位: s)的最大值;H=(NN+EE)/(N+E), 为东西和南北分量面波周期加权平均;是震中距(单位: °)。NEIC 测定的s(20)则根据 WWSSN-LP 地震仪的仿真记录, 采用垂直向面波资料, 然后根据下式[11]来计算: s(20)=lg(Z/Z)+1.66lg()+3.3, 20°<<160°, 18s 本文在有限断层模型和台站处的地震波记录基础上, 通过式(6)~(9)计算面波震级和矩震级, 并比较和讨论引起两者差异的原因。 图 6 展示 6 种模拟震例的面波震级(s,s(20))随子断层破裂持续时间(r)、破裂速度(r)和破裂长度()的变化曲线, 可以观察到如下特征。 1)随着r增加, 面波震级下降且不存在阈值。r= 30s 时, 面波震级比参考模型r= 10s 时约小 1级。r约为 20s 时,s(20)明显大于s, 这是由WWSSN-LP 地震仪的幅频特性决定的。需要指出的是, 如果r继续增加, 面波幅度还会进一步降低, 但辐射面波的优势周期(>30s)超出计算s和s(20)所使用面波的周期范围, 即此时利用式(6)和(7)计算的面波震级不能正确地反映面波的能量。 2)随着r增加, 面波震级增大, 其变化速率从陡变缓, 最后逐渐接近将整个断层面视为点源的计算结果。这是因为当r较小时, 子断层的波场到达台站的时间相差较大, 波形相互错开, 导致叠加的面波幅度较小; 当r较大时, 所有子断层几乎同时破裂, 加上震中距远大于破裂尺度, 子断层波场叠加的结果与点源激发的波场相似。 3)随着增加, 面波震级减小。原因在于破裂长度越大, 断层面的平均滑动量越小, 且相隔较远的子断层的波场到达同一个台站的时间差增加, 导致面波振幅减小。 4)震源参数相同时, 双侧破裂的面波震级大于单侧破裂。这是因为可将双侧破裂视为两个破裂长度减半的单侧破裂的叠加, 由于破裂长度减小, 面波震级增加, 因此双侧破裂的面波震级较高。 总体而言,w不变的情况下, 如果地震的总破裂持续时间(a)减少(r增大, 或和r减小), 则面波震级增大; 如果a增加(r减小, 或和r增大), 则面波震级减小(图 7(a)和(b))。 通过对比可以发现,s比s(20)平均大 0.23级, 存在系统性偏差(图 8)。s整体偏大的主要原因是CENC 与 NEIC 使用的量规函数不同, 式(6)采用的数字 3.5 大于式(7)采用的数字 3.3。另一方面, 图 7 (c)显示s−s(20)差值与 lg(a)明显负相关, 正交回归关系式为s−s(20) = −1.13lg(a) + 1.86, 相关系数为−0.73。a< 30s 时, 辐射的面波优势周期较小, 此时s比s(20)大 0.2~0.6 级(图 7(c)), 中国大陆强震 6~7 级居多(表 1), 而 6~7 级地震的平均持续时间为 6~25s[13], 这也可能是部分震例中 CENC测定的面波震级比 NEIC 显著偏大的原因之一。 模拟结果表明, 矩震级相同的地震, 其面波震级差别可高达 1 级(图 6), 这与不同震源参数下地震辐射能量不同有关。Vassiliou 等[14]给出地震辐射能的估算公式: 其中,和分别为 P 波和 S 波的波速, 依据 AK135模型,=5.80km/s,=3.46km/s;()为整个地震的归一化震源时间函数。我们通过(10)式来探究面波震级与辐射能之间的关系, 结果如图 9 所示, 面波震级与辐射能的对数 lg线性正相关。通过最小二乘拟合, 得到两者之间的转换公式为 从上往下, Mw分别为6.8, 7.2和7.5; 实线和虚线分别表示单侧破裂和双侧破裂; 黑线和灰线分别表示Ms和Ms(20) 图6 面波震级随震源参数的变化曲线 Fig. 6 Surface-wave magnitude variation curves with source parameters lg=1.8678s(20)+0.9251,(11) lg=1.7856s+1.1089,(12) 相关系数分别为 0.96 和 0.88。Choy 等[15]计算了 NEIC记录的 397 个实际震例的辐射能, 推导出与s(20)的经验关系式为 lg= 1.5s(20) + 4.4 (图 9 中虚线)。式(11)估算的辐射能比 Choy 等[15]的结果小 0.5~1 个数量级(6.5 ≤s(20) ≤ 8), 这是可以理解的。一方面, 本研究中波形的采样率为 1sps, 导致计算辐射能时的最高频率为 0.5Hz; 另一方面, 本文假定子断层震源时间函数为一个简单的三角形, 震源谱含较少的高频成分。实际上, 地震波的高频部分(大于拐角频率)携带了超过 80%的能量[16], 所以式(11)和(12)中的表征地震辐射的低频能量, 与优势周期较长的“单色”面波震级[17]具有极强的相关性, 而宽频带体波震级能够更好地反映地震辐射的高频能量[18]。 总而言之, 中国大陆强震面波震级s高于国际主流机构测定的矩震级w和面波震级s(20), 这与震级计算公式和仿真仪器的差异, 以及不同震级标度所示的物理意义不同有关[19]。为了与国际接轨, 依据我国 2017 年发布的震级测定新标准《地震震级的规定》(GB17740—2017)[10], 应将w作为重点测定的震级, 在及时测定地震矩的前提下, 优先选择w对外发布[19]。另外, 针对近震震级大于4.5 的浅源地震, 应使用宽频带面波震级s(BB)取代s作为对外发布的面波震级[19]。s(BB)是在垂直向的原始速度记录上测算的, 量规函数与s(20)相同, 平均偏差为 0.05[4], 并且s(BB)的优势周期为 3~60s, 比s和s(20)使用的频带更宽, 能更好地衡量地震的强度[19]。需要注意的是, 无论是面波震级还是矩震级, 都存在“单色性”的局限, 无法全面地反映地震激发的地震波能量大小。为此, 未来首选的震级标度应当是快速且准确地确定地震波的能量震级, 以便更好地对应地震造成的震感和破坏程度。 图7 Ms, Ms(20)以及两者震级差与地震总破裂持续时间(Ta)的关系 图8 Ms与Ms(20)震级差数量分布 本文通过断层的数值模拟和理论格林函数计算面波波场, 研究矩震级不变情况下, 子断层破裂持续时间(r)、破裂速度(r)和破裂长度()这 3 个震源参数对面波震级的影响, 得到以下结论。 实线为本文模拟的面波震级与辐射能的正交最小二乘拟合线, 虚线为Choy等[15]根据实际震例推导的经验关系lgE=1.5Ms(20)+4.4 1)总体而言, 这 3 个参数都是通过改变地震的总破裂时长来影响面波震级, 总破裂时间缩短(r和减小, 或r增大)时, 面波震级增大, 反之亦然。 2)由于计算公式和仿真仪器的不同,s总体上比s(20)偏高 0.23 级, 当地震持续时间较短时,s显著大于s(20), 最大差值可达 0.6 级。 3)矩震级对破裂模式和过程不敏感, 面波震级强烈受震源谱影响, 与地震辐射的低频能量有很强的相关性。不同的震级标度以各自的优势周期表征了地震波的基本特征, 反映了地震波信号在该优势周期的强弱程度, 都有其特定的意义和价值, 彼此不宜强行换算和比较。 我国测定的强震面波震级客观上存在比矩震级偏大的情况, 这其中既有中国大陆强震特定震源特征的原因, 也与我国特定的面波震级测定公式相关。一方面, 中国大陆多数强震为板内地震, 可能存在较高的应力降以及较短的破裂持续时间和破裂长度, 导致面波震级相对于矩震级偏高; 另一方面, 我国测定面波震级公式的量规函数比 NEIC 大 0.2。上述两大因素共同导致我国测定的强震面波震级系统性地高于矩震级。 [1] Scordilis E M. Empirical global relations convertingsandbto moment magnitude. Journal of Seis-mology, 2006, 10(2): 225–236 [2] 翟璐媛, 张立文, 任克新, 等. 中国台网数字化后与美国地震台网面波震级对比分析. 地震地磁观测与研究, 2015, 36(2):19–25 [3] 沙海军, 吕悦军. 中国地震台网面波震级与矩震级统计关系. 地震地磁观测与研究, 2018, 39(6): 31–36 [4] 刘瑞丰, 陈运泰. 震级的测定. 北京: 地震出版社, 2015 [5] Aki K, Richards P G. Quantitative seismology. 2nd edition. Sausalito: University Science Books, 2002 [6] Zhang Y, Feng W P, Chen Y T, et al. The 2009 L’Aquilaw6.3 earthquake: a new technique to lo-cate the hypocentre in the joint inversion of earth-quake rupture process. Geophysical Journal Interna-tional2012, 191(3): 1417–1426 [7] Kennett B L N, Engdahl E R, Buland R. Constraints on seismic velocities in the Earth from traveltimes. Geophysical Journal International, 1995, 122(1): 108–124 [8] Montagner J P, Kennett B L N. How to reconcile body-wave and normal-mode reference Earth models. Geophysical Journal International, 1996, 125(1): 229–248 [9] Wang R J. A simple orthonormalization method for stable and efficient computation of Green’s functions. Bulletin of the Seismological Society of America, 1999, 89(3): 733–741 [10] 刘瑞丰, 陈运泰, 许绍燮, 等. GB17740—2017 地震震级的规定. 北京: 中国标准出版社, 2017 [11] IASPEI. Summary of magnitude working group reco-mmendations on standard procedures for determining earthquake magnitudes from digital data [EB/OL]. (2013–03–27) [2022–06–22]. http://www.iaspei.org/ commissions/commission-on-seismological-observation- and-interpretation/Summary_WG_recommendations_ 20130327.pdf [12] Kanamori H. The energy release in great earthquakes. Journal of Geophysical Research, 1977, 82(20): 2981 –2987 [13] Bormann P, Wendt S, DiGiacomo D. Seismic sources and source parameters // New manual of seismolo-gical observatory practice 2 (NMSOP2). Potsdam: Deutsches GeoForschungsZentrum, 2013: 1–259 [14] Vassiliou M S, Kanamori H. The energy release in earthquakes. Bulletin of the Seismological Society of America, 1982, 72(2): 371–387 [15] Choy G L, Boatwright J L. Global patterns of radia-ted seismic energy and apparent stress. Journal of Geophysical Research: Solid Earth, 1995, 100(B9): 18205–18228 [16] Ide S, Beroza G C. Does apparent stress vary with earthquake size?. Geophysical Research Letters, 2001, 28(17): 3349–3352 [17] 陈运泰, 刘瑞丰. 地震的震级. 地震地磁观测与研究, 2004, 25(6): 1–12 [18] 宋潇潇, 吴忠良, 蒋长胜, 等. 矩震级及震源机制相似地震的辐射能量差别——2014 年鲁甸地震与景谷地震宽频带体波震级的比较. 中国地震, 2016, 32(4): 653–662 [19] 刘瑞丰, 陈运泰, 王丽艳, 等. 新的震级国家标 准的技术要点与主要特点. 地震地磁观测与研究, 2018, 39(1): 1–11 Analysis of the Reasons why Surface Wave Magnitude is Higher than Moment Magnitude in the Mainland of China from the Perspective of Source Rupture Parameters XU Yueyi, ZHANG Yong† School of Earth and Space Sciences, Peking University, Beijing 100871; † Corresponding author, E-mail: zhang-yong@pku.edu.cn The influence of the source parameters onsis studied through numerical simulations based on finite-fault models. The results show that thesis negatively correlated with earthquake rupture duration when moment magnitude remains unchanged. The source parameters that can impact the rupture duration contain the sub-fault duration, rupture velocity, and rupture length. Among them, the sub-fault duration and rupture length is negatively correlated withs, while the rupture velocity is positively correlated withs, if the moment magnitude remains unchanged. The fact that the measuredsof strong earthquakes in the mainland of China are significantly larger than moment magnitudes may be due to two reasons. First, the strong earthquakes in the mainland of China are mostly intraplate earthquakes with relatively higher stress drop values, which may have short rupture duration and rupture length. Secondly,sdetermined by China Earthquake Networks Center (CENC) is systematically larger thans(20) determined by National Earthquake Information Center. surface wave magnitude; moment magnitude; source parameters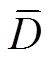

2 结果与讨论


3 结论

