改进混沌麻雀搜索算法及其在冗余机械臂逆运动学求解中的应用
2023-05-30于权伟李光谢楚政吴陈诚薛晨慷
于权伟,李光,谢楚政,吴陈诚,薛晨慷
(湖南工业大学 机械工程学院,湖南株洲 412007)
机器人运动学包括正运动学和逆运动学。前者是在工作空间内随机选取一组关节角来获得机器人末端执行器的姿态,其解具有唯一性;后者是给定目标位姿来求与之对应的关节角,其解不唯一。目前常见理论方法有代数法[1]、几何法[2]和数值法[3]等。
解析法和几何法虽可求得机械臂逆运动学封闭解,但机械臂需满足Pieper 结构。针对不满足Pieper准则的机械臂无法分离出独立的变量,很难求出逆运动学封闭解。冗余机械臂就属于这一类,但冗余机械臂比满足特殊结构的机械臂更加灵活,具有避免机械臂处于奇异位形、防止关节超过关节约束的优点,但其求逆运动解却十分困难[4]。
随着机械臂结构的复杂化和计算机的发展,学者们将智能优化方法应用于求机械臂逆运动解中。智能算法应用广泛,其主要思想是将机械臂关节运动方程转化为优化问题来求逆运动学解[5]。这类算法主要包括遗传算法[6]、粒子群算法[7]及神经网络算法[8]等。
石建平[9]提出多策略混合协同进化机制的改进粒子群优化算法,对冗余机械臂进行逆运动学求解;李梅红[10]提出一种动态变步长的果蝇算法用于求冗余机械臂逆运动学解;文献[11]采用机械臂运动所产生的动能和多次重复运动作为优化问题,以机械臂关节运动限制为约束,将冗余机械臂逆运动学求解转化为凸优化问题来进行求解。肖帆[12]提出改进自适应协方差矩阵进化策略对7 自由度仿人臂机器人进行逆运动学求解。文献[13]利用麻雀觅食过程提出一种新型智能算法搜索—麻雀搜索算法(Sparrow search algorithm,SSA)。利用基准函数进行多次实验来测试SSA 性能,并与其他算法进行性能比较。结果表明,SSA 在精度、收敛速度、稳定性和鲁棒性方面均优于其他算法。吕鑫等[14]提出一种混沌麻雀搜索优化算法(Chaos sparrow search algorithm,CSSA),并在基准函数上进行多次实验来进行仿真实验,表明CSSA 能改善SSA 易陷入局部最优的问题。
本文提出一种自适应混沌麻雀搜索算法(Adaptive chaos sparrow search algorithm,ACSSA)用于求冗余机械臂的逆向运动学解。首先,利用佳点集均匀分布特性生成初始化种群;其次,引入动态自适应权重,可平衡全局和局部搜索能力,提高种群多样性;最后,引入高斯变异,加强局部搜索能力,提高搜索精度。同时,产生Tent 混沌序列,防止陷入局部最优;通过建立仿真实验,将ACSSA 与CSSA、SSA 分别在空间点到点运动中以及空间连续轨迹跟踪中进行对比,结果表明ACSSA 收敛速度快、精度高、鲁棒性好。
1 麻雀搜索算法
SSA 是根据麻雀种群觅食和反捕食行为提出的智能优化算法。麻雀觅食过程中种群分为两个部分:发现者和跟随者,同时还设置侦察者作为预警机制。发现者负责寻找食物并引导整个种群,跟随者通过跟随发现者来觅食,同时选取一定比例的麻雀进行侦察,当意识到危险时会发出警报信号,做出反捕食行为。
SSA 中,发现者占整个麻雀种群的10% ~ 20%,其位置更新为
式中:t为当前迭代次数;T为最大的迭代次数;α为(0, 1]的均匀随机数;Q为服从标准正态分布的随机数;L为1 ×d元素均为1 的矩阵;R2∈[0, 1]和ST∈[0.5, 1]分别表示预警值和安全值。
跟随者位置更新为
其中
侦察者位置更新为
式中:β为控制步长参数,服从N(0, 1)的随机数;K为麻雀移动的方位,同时也是步长控制参数,是一个随机数且K∈[-1, 1];e为一个极小数,防止分母为0 的情况发生;fi为第i只麻雀的适应度值;fg和fw分别为当前麻雀种群的最优和最差适应度值。
2 改进麻雀搜索算法
虽然SSA 具有较强的全局搜索能力和较快的收敛速度,但在进化后期存在种群单一和容易陷入局部最优等问题。为增加种群多样性,改善算法易陷入局部最优,本研究在CSSA 基础上做如下改进:
1)利用佳点集均匀分布的特点生成初始化种群;2)在发现者更新位置时引入自适应动态权重。
2.1 佳点集
单位空间中均匀分布的点集合成为佳点集。佳点集只有佳点个数和维数两个参数。因此,利用该特性初始化种群,便于加快收敛速度,保持种群多样性。
佳点集公式[15]如下:
式中:d和m均为维度;{rn×i}表示rn×i的小数部分;Pbi(n)∈[0,1],可经过式(6)映射至搜索空间,即
图1a)为[0,1]范围内的500 个粒子经过Tent混沌迭代500 代后的种群分布图。可看出在[0.2,0.3]和[0.6,0.7]之间相对分布误差较大。图1b)采用佳点集在[0,1]范围内随机生成500 个粒子,粒子呈均匀分布,在进化过程中可增加种群多样性,避免陷入局部最优。
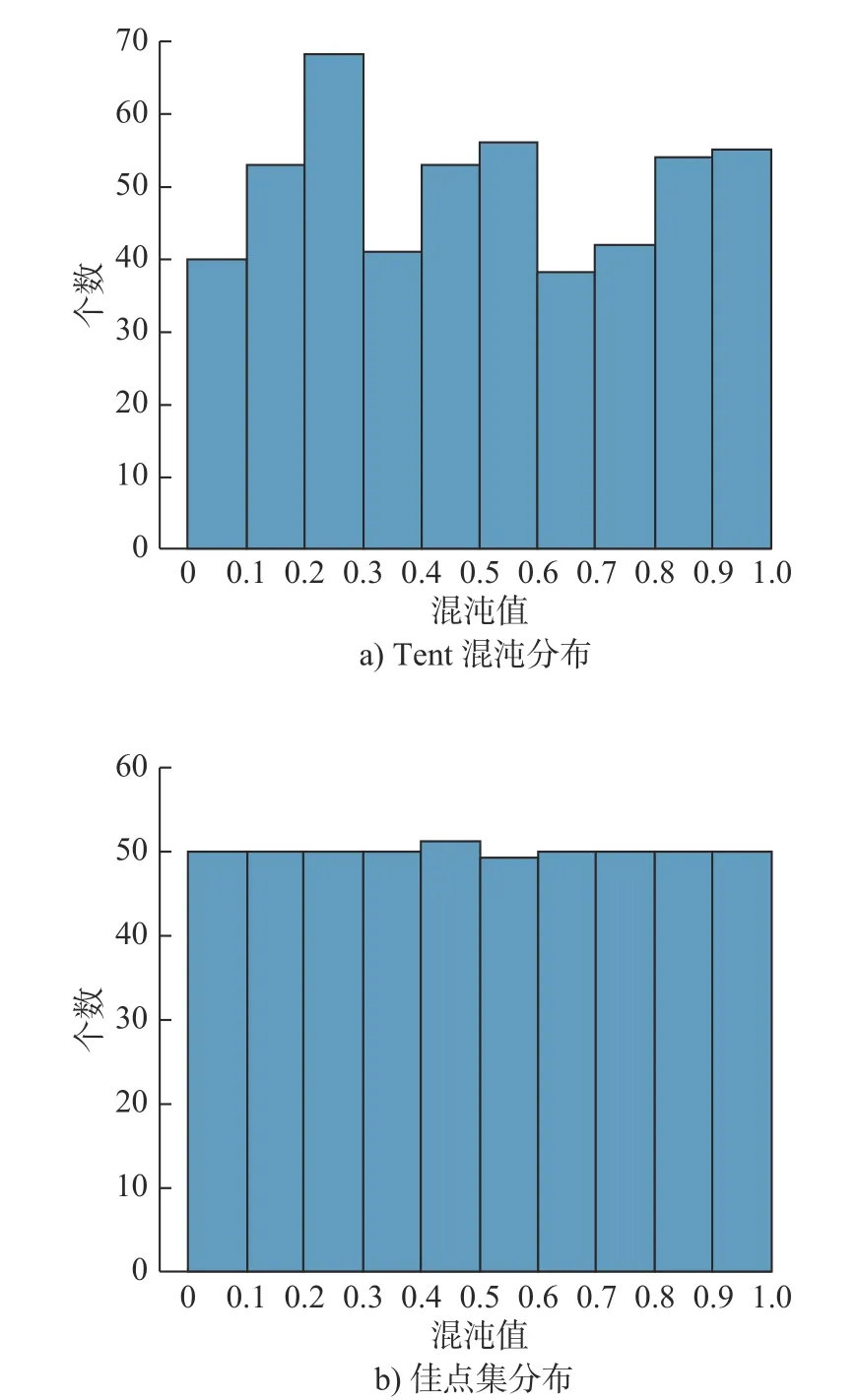
图1 混沌序列分布
2.2 动态自适应权重
算法进化过程分为全局搜索和局部搜索。进化初期由全局搜索发挥主要作用来找到全局最优解[16]。为了防止陷入局部最优,可引入上代全局最优解,使得发现者位置受到上代的影响。因此,引入动态权重 ω,既可以平衡全局搜索和局部搜索,也可防止陷入局部最优。
式中q∈[0, 1]服从均匀分布。
图2为式(8)迭代400 次后的权重动态曲线图,呈振荡形递减。在全局搜索时有较大的值,加大全局搜索能力,快速搜寻全局最优解;在局部搜索时有较小的值,加大局部搜索能力。
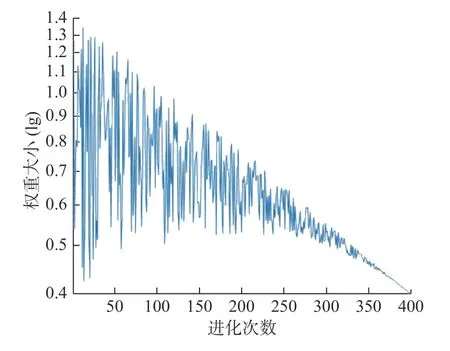
图2 动态权重策略
改进后发现者位置更新
3 ACSSA 算法步骤
步骤1 设置初始化参数,包括麻雀数量、发现者和跟随者之间比例、最大迭代次数或阈值;
步骤2 在关节范围内利用佳点集生成初始种群;
步骤3 计算每只麻雀的适应度并找到当前最佳和最差的个体;
步骤4 确定发现者和跟随者的数量,式(9)更新发现者位置,式(2)更新跟随者位置,式(4)更新警戒者位置;
步骤5 每经过一次迭代后,重新计算每只麻雀的适应度值和麻雀种群的平均适应度值,并进行比较。当每只麻雀的适应度值小于平均适应度值时进行高斯变异,如果新位置比旧位置优,则更新旧位置;当每只麻雀的适应度值大于平均适应度值时进行Tent 扰动,如果新位置比旧位置优,则更新旧位置;
步骤6 计算适应度值,更新麻雀位置;
步骤7 是否满足输出条件,满足则输出结果,否则重复步骤3 ~ 步骤6。
4 ACSSA 在冗余机械臂逆向运动学分析中的应用
4.1 冗余机械臂正向运动学
图3为一类7 自由度冗余机械臂的结构简图,利用标准D-H[17]法进行正向运动学建模,机械臂各关节D-H 参数如表1 所示。

表1 冗余机械臂各关节D-H 参数

图3 冗余机械臂结构简图
相邻连杆{i}坐标系相对于{i-1}坐标系齐次变换矩阵为
式中:s= sin;c= cos。根据式(10)和表1 的D-H参数,可求得机械臂末端位姿矩阵为
式中:R3×3为姿态矩阵;p为位置矢量。
4.2 构建适应度函数
为了求取机械臂实际位姿与目标位姿之间的误差,以机械臂的接近矢量a和位置矢量p加权和来构建适应度函数,且二者均与机械臂θ1~θ6有关,而θ7由前6 个关节角可求,因此设θ7= 0。
式中:α和β分别为权值系数。
在实际应用中,机械臂的位置矢量通常为103数量级。姿态矩阵由正余弦函数联立得出,通常数量级小于1。为防止局部收敛,在计算之前须对姿态矩阵和位置矢量数量级进行归一化处理[18]。
冗余机械臂的逆运动学存在无数组解,而式(12)每次只求得一组点到点的解。要想在空间运动中找到最柔顺(消耗能量最小)的连续轨迹,且要求空间运动轨迹平滑连续时,可构建适应度函数进行求解[19],即:
式中:θini为初始关节角;f2为关节运动最小变化量;γ为权值系数。
5 仿真实验与结果分析
为检验ACSSA 在求冗余机械臂逆运动学解中的可行性与有效性,通过计算机建立仿真实验将ACSSA、CSSA 与SSA 分别应用于空间点到点运动和空间连续轨迹运动,进行对比验证两种工况。
5.1 参数设置
3 种算法的初始参数:麻雀的种群均为S= 30;最大进化次数均为Nmax= 200;发现者个数的初始值均为Np =0.2S;侦察预警麻雀的个数均为种群规模的20%。适应度函数中的权值系数分别取α=0.003 3,β =1,γ =0.25,算法的终止条件均为Nmax=200 或f1< 10-5,ACSSA 中ωmax= 0.9,ωmin= 0.4。
5.2 实验结果分析
给定一组关节角θ= [1 1 1 1 1 1] rad,代入式(11)求得正向运动学T,即
针对式(15)的末端位姿,3 种算法分别在工作空间内对冗余机械臂求逆向运动学解,结果如表2所示。图4为3 种算法位姿求解曲线对比图,结果表明:ACSSA 和CSSA 明显都优于SSA;ACSSA 达到收敛条件时的速度比CSSA 提高了37%左右,若不设置阈值将继续搜索下去;而SSA 在10-2左右就停止了搜索。
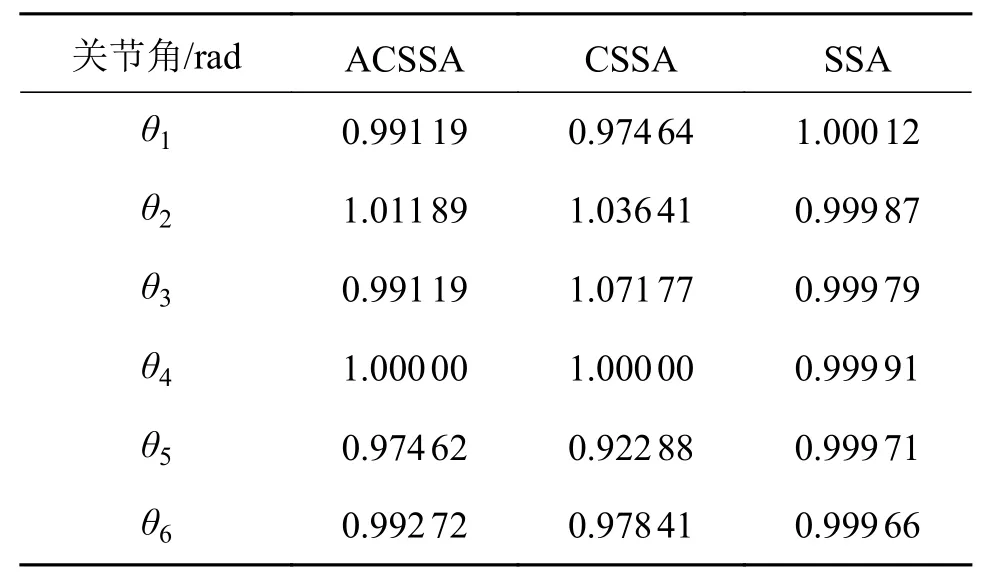
表2 3 种算法各自求得的一组逆运动学解

图4 3 种算法位姿求解曲线对比图
为验证算法的稳定性,同时避免结果的偶然性,将3 个算法独立对位姿求解200 次,位姿误差f1结果如表3,位姿收敛曲线图如图5 所示。
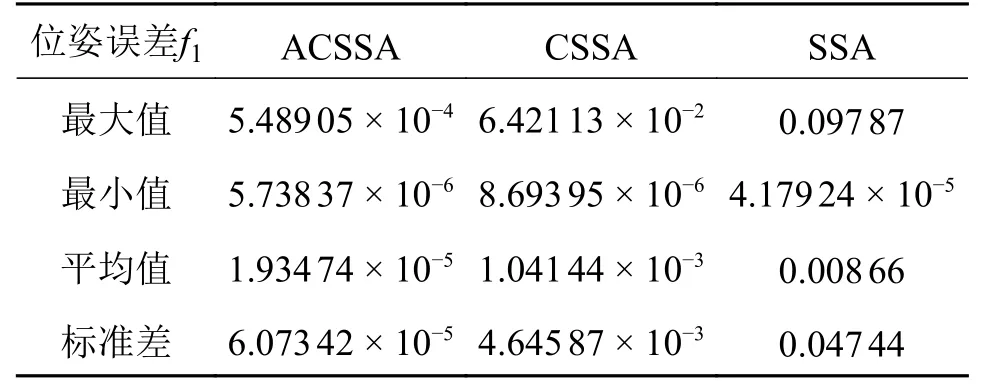
表3 3 种算法独立运行200 次时f1 结果 mm
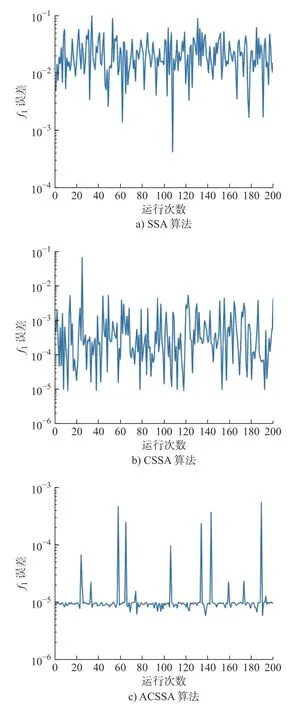
图5 3 种算法独立运行200 次的位姿收敛曲线
表3表明ACSSA 算法不仅在收敛精度上比CSSA 算法和SSA 算法都高了两个2 个数量级,而且在算法稳定性上也比CSSA 算法、SSA 算法分别高出2、3 个数量级。从图5 中的收敛曲线来看ACSSA 在求解过程中波动较小,位姿误差可维持在10-5数量级。
图6为ACSSA 独立运行200 次后求得的关节角范围图,从图6 看求解结果均在关节约束范围内。

图6 ACSSA 算法求得的各关节角
为进一步证明ACSSA 精度高、速度快、鲁棒性好的特性,现给定一段空间连续轨迹,并均匀采样200 个点作为理论值,建立仿真实验。分别用ACSSA、CSSA、SSA 进行验证并对比分析结果。
轨迹方程为:式中:t的步长为π/50;轨迹每一个点的姿态均为[1 0 0;0 1 0;0 0 1]。设置机械臂的初始关节θini=[0 0 0 0 0 0],利用式(14)求解空间轨迹上200 个理论值的逆解,此时关节角范围设置为[-π,π]。
图7为空间轨迹中采样点位姿的对比图,可看出仿真轨迹与期望轨迹基本重合。

图7 ACSSA 的轨迹仿真
表4为3 种算法的轨迹理论点和实际点位置绝对误差,结果表明:在对空间连续轨迹求解时,在计算值和理论值位置绝对误差精度和稳定性两个评定指标上,ACSSA 较CSSA 提高了1 个数量级,较SSA 提高了6 个数量级。充分验证了ACSSA 具有精度高、可避免陷入局部最优等特性。

表4 轨迹理论点和实际点位置绝对误差 mm
6 结论
1)提出一种自适应混沌麻雀搜索算法(ACSSA),利用佳点集均匀分布特性生成初始化种群,避免在迭代过程中陷入局部最优;并引入动态权重平衡,提高全局和局部搜索的能力,防止种群单一。
2)将ACSSA 应用到求冗余机械臂逆向运动学解中,在空间点对点运动中,以位姿误差作为适应度函数,得到的仿真实验结果表明ACSSA 在满足精度的前提下,收敛精度和算法稳定性上比CSSA、SSA 均高出了2、3 个数量级。
3)在空间连续轨迹运动中,以位姿误差和关节位移最小的加权和作为适应度函数,得到的计算值和理论值的位置绝对误差精度可达10-5mm,稳定性可达10-4mm。
4)对于求冗余机械臂逆运动学解的问题,ACSSA收敛精度以及收敛速度显著提高,充分证明了算法改进的可行性。
