基于序列凸规划的拦截弹中制导轨迹优化

李炯 张锦林 邵雷 李万礼 贺杨超

引用格式：李炯，张锦林，邵雷，等.基于序列凸规划的拦截弹中制导轨迹优化［J］.航空兵器，2023，30（1）：37-43.

LiJiong，ZhangJinlin，ShaoLei，etal.MidcourseGuidanceTrajectoryOptimizationofInterceptorMissileBasedonSequentialConvexProgramming［J］.AeroWeaponry，2023，30（1）：37-43.（inChinese）

摘要：針对强非线性多约束条件下拦截弹中制导轨迹优化问题，基于序列凸规划方法和捕获区域，提出一种针对固定时间约束下的轨迹优化算法。序列凸优化方法求解复杂多项式具有高效的计算效率，但在轨迹优化问题中应用序列凸规划有控制变量的强非线性和固定时间内终端约束难以收敛两大难点。首先，采用仿射变量将问题转化为仿射系统，并将仿射系统进行凸化与离散化，来解决非线性问题，然后，提出一种终端约束加权松弛化方法来解决固定时间内终端约束难以收敛问题，并将中制导问题转化为序列凸规划问题。仿真结果表明，所提算法能较快地生成符合多约束条件的拦截弹中制导轨迹。

关键词：序列凸规划；中制导；轨迹优化；捕获区域；多约束;高超声速;拦截弹

中图分类号：TJ765

文献标识码：A

文章编号：1673-5048（2023）01-0037-07

DOI：10.12132/ISSN.1673-5048.2022.0115

0引言

目前高超声速武器由于速度快、射程远等优势，对空天安全提出巨大的挑战［1-2］。拦截弹的中制导在拦截此类目标时，可以为具有飞行约束的末制导提供良好的拦截态势［3］，具有重要研究意义。

中制导轨迹优化是在拦截弹动力学模型基础上，根据预测的捕获区域，解算满足过程约束和终端约束的制导指令［4-5］。文献［6］考虑拦截弹捕获区，提出一种基于高斯伪谱法的中制导轨迹优化方法，具有很高的精度。文献［7］提出了一种基于邻域最优控制理论的高超声速拦截中弹道在线优化修正算法。文献［8］提出一种终端时间固定的广义拟谱模型预测静态规划方法，成功用于中制导拦截。文献［9］在模型预测静态规划理论的基础上，提出一种多阶段最优轨迹规划与制导方法。虽然模型预测静态规划能应用于中制导，但拦截弹拦截过程中，可能存在超出过程约束的现象。

近年来，凸优化方法因为解的存在性［10］和求解复杂多项式高效的计算效率，在航空航天领域得到了广泛的应用［11］。文献［12］将强非线性的飞行器再入的最优控制问题，转化成凸优化问题。文献［13］结合基于凸优化的算法和伪谱非线性规划方法，构建了一个两阶段轨迹优化框架。文献［14-15］介绍了一种凸化非凸约束的松弛技术，采用正则化技术对松弛程度进行约束。文献［16］结合伪谱方法和凸优化方法，提出一种新的大气再入制导阻力能量方案，能够无损凸化公式。文献［17］将多约束的再入问题表述成一个容易求解的二阶锥规划序列。文献［18］提出一个非常规的收敛条件，使序列凸规划方法以较少的迭代次数收敛到原问题的可行解。文献［19］提出一种基于自定义自适应网格细化的序列凸规划方法，在保证收敛解可行性的同时，可以减少网格点的数量。文献［20］提出一种拉格朗日伪谱凸优化方法，在考虑过程约束的同时，解决火星大气进入末端高度最大化问题。以上文献表明，凸优化方法在解决非线性多约束问题上有很多的应用与优势。

拦截弹中制导拦截问题是强非线性多约束的轨迹优化问题。首先，通过仿射变量将拦截弹的非线性动力学模型，转化为仿射系统动力学模型。其次，以目标的预测点形成的捕获区域为终端约束，并提出终端约束加权松弛化方法解决固定时间中制导终端约束难以收敛问题。然后，以过载、热流密度、动压等作为过程约束，将模型与约束依次松弛化、线性化和离散化，将固定时间的中制导拦截问题转化为序列凸规划问题。最后，通过多种场景对本文算法的有效性与鲁棒性进行了验证。

1中制导问题的建立

1.1仿射动力学模型和控制约束

拦截弹在中段制导阶段采用无动力滑翔，动力学模型建立在地面固定坐标系上［14］，x轴和z轴分别指向东和北，和h轴组成右手系，忽略地球自转影响，拦截弹在平坦的地面上空，动力学模型经无量纲化处理后如下：

x·=Vcosθcosψ

z·=Vcosθsinψ

h·=Vsinθ

V·=－D－sinθ/r2

θ·=Lcosσ/V－cosθ/（Vr2）

ψ·=Lsinσ/（Vcosθ）（1）

式中：（x，z，h）为拦截弹的位置坐标；r=1+h为地心到拦截弹的直线距离；V为地球相对速度，以g0re比例缩放，g0为在地球表面re处的重力加速度；θ为弹道倾角；ψ为弹道偏角。

无量纲阻力和升力加速度如下：

L=0.5ρ（Vg0re）2CLS/（mg0）（2）

D=0.5ρ（Vg0re）2CDS/（mg0）（3）

式中：S为拦截弹受力参考面积；CD和CL为拦截弹的阻力系数和升力系数，与攻角α和马赫数有关；m为拦截弹的质量，大气密度ρ（h）=ρ0e－hre/H，ρ0=1.225kg/m3，H=7.11km。

定义控制变量归一化系数λ：

λ=CL/CL（4）

CD=CD［1+λ2］/2（5）

式中：C*L和C*D分别为某马赫数下最大升阻比对应的升力系数和阻力系统，可通过气动数据表插值得到。

由上式，可将式（2）～（3）转化为

L=L^λ（6）

D=D^［1+λ2］/2（7）

式中：升力加速度L^=qSC*L；阻力加速度D^=qSCD/2。

目前的动力学模型仍不是控制仿射系统，下面构建仿射变量：

u1=λcosσu2=λsinσu3=λ2（8）

通过仿射变量可将式（1）转化为

dx/dt=Vcosθcosψdz/dt=Vcosθsinψdh/dt=VsinθdV/dt=－0.5［1+u3］D^－sinθ/r2

dθ/dt=u1L^/V－cosθ/（Vr2）

dψ/dt=u2L^/（Vcosθ）（9）

在仿射系统中，控制量u必须满足：

u21+u22=u3（10）

本文假设归一化系数λ非负，上限为λ-，则u3的取值范围为

0≤u3≤u-3（11）

式中：u-3=λ-2。假设倾侧角σ的取值范围在区间（－90°，90°）内为［σmin，σmax］，则

u1tan（σmin）≤u2≤u1tan（σmax）（12）

1.2过程约束和边界约束

拦截弹中制导拦截过程中需要满足过程约束，否则可能出现拦截弹失控现象。其中，过程约束主要有过载约束、热流密度约束及动压约束等：

n=L2+D2=u3L^2+（1+u3）2D^2/4≤nmax（13）

Q·=kQρ0.5（Vg0re）3.15≤Q·max（14）

q=0.5ρ（Vg0re）2≤qmax（15）

过程约束可写为

L（h，V，u3）≤L-（16）

式中：L-为拦截弹过程约束允许的最大值。

假设拦截弹中制导的初始状态为x0，初始时刻为t0，则初始条件约束为

x（t0）=x0（17）

拦截弹的终端约束由捕获区域确定，最佳终端条件为零控拦截状态。假设预测的拦截弹中制导结束时的零控拦截状态是xp=［xp;zp;hp;～;θp;ψp］。上述零控拦截状态对拦截弹的速度大小没有要求，但为了有效摧毁目标，拦截弹速度越大越好，速度约束在目标函数中加以体现。

拦截弹中制导结束时刻为tf，则终端约束为

x（tf）=xp（18）

由于拦截弹是在指定时间飞向指定空域，如果终端约束采用式（18）强等式约束，可能会造成可行域内无解的情形。本文提出终端约束加权松弛化方法对强等式约束式（18）进行松弛，以确保问题存在可行解，表达如下：

xf－xp=κ1ω1

zf－zp=κ1ω2

hf－hp=κ1ω3

θf－θp=ω4

ψf－ψp=ω5（19）

式中：松弛系数ω=［ω1，ω2，ω3，ω4，ω5］在目标函数中约束；κ1为权重系数，为状态量的权重接近。

1.3目标函数和中制导问题描述

为了有效摧毁目标，以拦截弹的最大速度为主要目标函数，加上终端约束松弛系数，目标函数为

J0=－c1Vf+c2ωTω（20）

综上所述，原始的拦截弹中制导拦截问题就转化成终端时间固定的最优控制问题P1：

P1：minJ0

s.t.式（9）～（12），（16）～（17），（19）

2凸化与离散化

2.1凸化

问题P1仍是一个非线性强约束问题，需要对仿射变量松弛化和对约束线性化，才能将问题P1转化成凸优化问题P2，之后将问题P2进行离散化，转化成序列凸规划问题P3，以便于算法求解。

2.1.1仿射变量松弛化

从式（10）～（12）可以看出，仿射变量约束为强等式约束，强约束会造成问题P1的非凸，为将问题P1凸化，将式（10）松弛为

u21+u22≤u3（21）

为保证松弛后的仿射变量的有效性，目标函数上增加c3∫tft0ψ（t）dt项，来确保仿射变量满足式（10）约束。

2.1.2约束的线性化

式（9）可以表述为

x·=f（x）+B（x）u（22）

f（x）=VcosθcosψVcosθsinψVsinθ－0.5D^－sinθ/r2cosθ/（Vr2）0（23）

B（x，t）=03×103×103×1

00－0.5D^

L^/V00

0L^/（Vcosθ）0（24）

u=［u1，u2，u3］（25）

利用一階泰勒展开式对式（20）关于参考轨迹（x*，u*）线性化可得

x·=f（x*）+A（x*）（x－x*）+B（x*）u（26）

式中：A（x*）=f（x）xx=x*。

利用一阶泰勒展开式对式（16）关于参考轨迹的（h*，V*，u*3）线性化可得

L（h*，V*，u*3）+L′·［h-h*，V-V*，u3-u*3］≤L-（27）

式中：L′=Lh，LV，Lu3。

综上所述，问题P1转化成了凸优化问题P2：

P2：minJ=－c1Vf+c2ωTω+c3∫tft0ψ（t）dt

s.t式（11）～（12），（17），（19），（21），

（26）～（27）

2.2离散化

问题P2是一个凸域内的无限维连续参数优化问题，无法直接进行优化迭代，所以将问题P2进行离散化，转化成有限维的序列凸规划问题P3，以便于计算机运算。

将时间域［t0，tf］分成N份，离散区间Δt=（t0－tf）/N，离散点序列i=0，1，2，…，N－1，N。

假设第k－1（k≥1）次迭代生成轨迹为（xk－1，uk－1），在第k次迭代过程中通过梯形法将式（26）离散化可得

xi=xi－1+Δt2［（A（k－1）i－1xi－1+Β（k－1）i－1ui－1+F（k－1）i－1）+（A（k－1）ixi+Β（k－1）iui+F（k－1）i）］（28）

式中：xi=x（ti）；ui=u（ti）；A（k－1）i－1=A（x（k－1）（ti－1））；B（k－1）i－1=B（x（k－1）（ti－1））；F（k－1）i－1=f（k－1）i－1－A（k－1）i－1x（k－1）i－1；f（k－1）i－1=f（x（k－1）（ti－1）。

为了减少问题P2在第k次迭代过程中可行解的寻优范围，采用变信赖域方法对可行解加以约束：

xi-x（k－1）i≤ξεxui-u（k－1）i≤ξεu（29）

式中：信赖域松弛系数ξ在目标函数中加以约束；εx与εu为状态量的信赖域区间。

同理可得，在第k次迭代过程中，式（27）可转化为

L′·［h-h（k-1），V-V（k-1），u3-u（k-1）3］+L（h（k-1），V（k-1），u（k-1）3）≤L-（30）

综上所述，无限维的问题P2转化成了有限维的问题P3，表述如下：

P3：minJ=－c1Vf+c2ωTω+c3∑Ni=0ψiΔt+c4ξ

s.t.式（11）～（12），（17）～（19），（21），

（28）～（30）

3序列凸规划算法

3.1算法求解步骤

由于原中制导问题P1具有强非线性，仅采用一次线性化来处理问题P1中的非线性动力学约束与过程约束，所求迭代解对于问题P1一般不可行。本文采用连续线性化方法，对非线性动力学约束与过程约束进行线性化，从而产生一系列迭代解序列。

序列凸规划算法是以相邻两次迭代解的最大偏差值作为收敛条件，满足该条件，则认为算法收敛并结束，迭代解为满足问题P1的最优可行解。收敛条件如下：

x（k+1）-x（k）≤δx

u（k+1）-u（k）≤δu（31）

求解步骤如下。

步骤1：令k=0，给出初始参考轨迹x0，初始参考控制指令（u01，u02，u03）。

步骤2：基于参考轨迹xk与参考控制指令（uk1，uk2，uk3）计算所需的迭代参数。

步骤3：求解问题P3，获得迭代解（xk+1，uk+1）。

步骤4：判断迭代解是否满足式（31），满足该收敛条件，则算法结束；否则，令k=k+1，进入步骤2。

4数值仿真

本文数值仿真过程均在IntelCorei7-105102.30GHz、8GRAM和Windows10操作系统的计算机上进行，并采用嵌入式圆锥求解器ECOS［21］求解问题P3。

拦截弹模型参数m0=900kg，S=0.4839m2，仿射变量λ的界限为［0，4.4016］，倾侧角σ的界限为［－60°，60°］。过程约束nmax=3.5g0，Q·max=1000kW/m2，qmax=150kPa。目标函数中的权重系数为c1=100，c2=10，c3=0.01，c4=0.01。终端约束权重系数κ1=0.001。中制导拦截初始状态为（0km，0km，40km，2500m/s，5°，0°）。

初始参考轨迹是拦截弹以最大归一化系数λ-飞行，z轴直接从起点指向终点，该轨迹生成方法具有生成速度快的优点。

序列凸规划算法信赖域约束为

εx=e5re，e4re，e4re，500g0re，10π180，10π180（32）

εu=［η-/2，η-/2，η-2/2］（33）

本文序列凸規划算法收敛域约束为

δx=e3re，e2re，e2re，50g0re，π180，π180（34）

δu=［η-/10，η-/10，η-2/10］（35）

4.1算法验证

以拦截弹状态（400km，25km，25km，～，0°，10°）为中制导终端约束，飞行时间为tf=175s，以拦截弹速度最大为主要目标函数，对本文算法进行验证。

中制导轨迹每次迭代后位置信息的变化如图1所示，其轨迹从初始参考轨迹逐渐向最终轨迹收敛，结果显示，第5次与第6次的迭代轨迹符合收敛域约束，即第6次迭代轨迹为最终收敛轨迹。

收敛轨迹的速度变化情况如图2所示，其速度变化符合图1（a）轨迹运动关系，中制导结束时，速度为1859.4m/s。

6次迭代求解的时间如表1所示，初始参考轨迹生成时间约为0.069s，总运算时间为6次轨迹求解时间加初始参考轨迹生成时间，约为1.829s。

收敛轨迹过程约束的变化情况如图3所示，过载、热流密度与动压过程约束均符合约束。其中，在100～150s之间过程约束存在凸起现象，这是因为收敛的轨迹高度呈现凹形曲线，空气密度曲线呈现凸形，进而导致过程约束呈现凸形曲线。

收敛轨迹的控制量变化信息如图4所示，其中控制量u1与u2可以用u3和倾侧角σ表示。收敛轨迹的控制量均满足控制量约束。

由仿真结果可得，本文算法能解决强非线性多约束问题，得到满足约束的中制导轨迹。

4.2鲁棒性分析

以不同弹道倾角为终端约束变化条件，以验证本文算法的鲁棒性。拦截弹终端约束为（350km，18km，26km，～，～，10°），弹道倾角分别取（-1°，1°，3°，5°，7°），飞行时间为tf=155s，以拦截弹速度最大为主要目标函数，对本文算法的鲁棒性进行分析。

在不同弹道倾角的终端约束下，拦截弹收敛轨迹的剖面图如图5所示。由图可知，在不同的彈道倾角下，拦截弹能在固定飞行时间内到达期望位置。

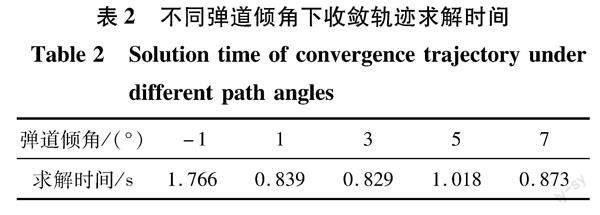
不同弹道倾角下收敛轨迹的求解时间如表2所示。求解过程中，最少迭代4次，最多迭代6次，轨迹收敛。

不同弹道倾角下收敛轨迹的速度变化情况如图6所示。由图可知，在上述仿真条件下，拦截弹到达同一期望位置时的弹道倾角越大，其速度越小。结合图5（a）可知，在上述高抛弹道中，终端弹道倾角越大，其高抛弹道的最低点越低，拦截弹的速度越小。

不同弹道倾角下收敛轨迹的弹道倾角和弹道偏角的变化情况如图7所示。最终弹道倾角与弹道偏角能收敛到期望角度。综上所述，本文优化方法能在不同终端状态约束条件下生成满足约束的中制导轨迹。

4.3优化方法对比

以拦截弹状态（400km，20km，24km，～，0°，10°）为中制导终端约束，飞行时间为tf=175s，以拦截弹速度最大为主要目标函数，对序列凸规划算法（SCP）和高斯伪谱法（GPM）进行对比。

本文算法与高斯伪谱法收敛轨迹的剖面图如图8所示。两者收敛轨迹并不重合，主要是由于两方法内部初始参考轨迹生成方法不同与配点方式不同造成的。本文算法迭代6次，求解的总时间为1.666s，高斯伪谱法的运算时间为6.619s，从时间上对比，本文算法求解中制导问题的速度更快。

两种优化方法终端误差如表3所示，高斯伪谱法表格显示误差由于小于保留位数，显示为0。从表3可以看出，高斯伪谱法的求解精度要高于本文优化方法。

两种方法收敛轨迹的终端速度变化如图9所示，本文算法的终端速度为1943.8m/s，高斯伪谱法的终端速度为1942.3m/s。终端速度相差仅1.5m/s，这与两者目标函数相同、终端约束相同有关。

两种方法收敛轨迹的过程约束与控制量的变化情况如图10所示，过程约束与控制量均未超出约束。

综上所述，两种方法都能解决强非线性多约束中制导问题，但本文算法比高斯伪谱法的求解速度更快，精度略差。

5结论

本文提出的针对目标捕获区域的中制导轨迹优化方法，能快速求解出满足约束的中制导轨迹。针对优化问题固定时间内终端约束难以收敛问题，提出一种终端约束加权松弛化方法，能避免收敛域内无解的情况，同时将中制导模型转化为仿射系统，以解决控制变量的强非线性约束。

进一步研究是寻找新的初始参考轨迹生成方法，靠近收敛轨迹的初始参考轨迹能减少收敛次数与问题求解时间。

参考文献：

［1］雷虎民，骆长鑫，周池军，等.临近空间防御作战拦截弹制导与控制关键技术综述［J］.航空兵器，2021，28（2）：1-10.

LeiHumin，LuoChangxin，ZhouChijun，etal.SummaryofKeyTechnologiesofInterceptorGuidanceandControlinNearSpaceDefenseOperations［J］.AeroWeaponry，2021，28（2）：1-10.（inChinese）

［2］张耀，宋鹏超，王菁华.俄新型高超声速导弹技术性能综述与分析［J］.飞航导弹，2019（2）：30-33.

ZhangYao，SongPengchao，WangJinghua.OverviewandAnalysisofTechnicalPerformanceofNewHypersonicMissilesinRussia［J］.AerodynamicMissileJournal，2019（2）：30-33.（inChinese）

［3］ZhouJ，LeiHM，ZhangDY.OnlineOptimalMidcourseTrajectoryModificationAlgorithmforHypersonicVehicleInterceptions［J］.AerospaceScienceandTechnology，2017，63：266-277.

［4］DennisME，HagerWW，RaoAV.ComputationalMethodforOptimalGuidanceandControlUsingAdaptiveGaussianQuadratureCollocation［J］.JournalofGuidance，Control，andDynamics，2019，42（9）：2026-2041.

［5］张锦林，李炯，雷虎民，等.有限过载的三维现实真比例导引的捕获区域［J］.系统工程与电子技术，2022，44（3）：986-997.

ZhangJinlin，LiJiong，LeiHumin，etal.CaptureRegionof3DRealisticTrueProportionalNavigationwithFiniteOverload［J］.SystemsEngineeringandElectronics，2022，44（3）：986-997.（inChinese）

［6］ZhouJ，ShaoL，WangHJ，etal.OptimalMidcourseTrajectoryPlanningConsideringtheCaptureRegion［J］.JournalofSystemsEngineeringandElectronics，2018，29（3）：587-600.

［7］LeiHM，ZhouJ，ZhaiDL，etal.OptimalMidcourseTrajectoryClusterGenerationandTrajectoryModificationforHypersonicInterceptions［J］.JournalofSystemsEngineeringandElectronics，2017，28（6）：1162-1173.

［8］谭一廷，荆武兴，高长生.考虑零控交班视窗角约束的拦截中制导设计［J］.宇航学报，2021，42（10）：1257-1270.

TanYiting，JingWuxing，GaoChangsheng.DesignofInterceptionMidcourseGuidancewithZeroEffortHandoverVisualAngleConstraint［J］.JournalofAstronautics，2021，42（10）：1257-1270.（inChinese）

［9］周聰，闫晓东，唐硕，等.大气层内模型预测静态规划拦截中制导［J］.航空学报，2021，42（11）：524912.

ZhouCong，YanXiaodong，TangShuo，etal.MidcourseGuidanceforEndo-AtmosphericInterceptionBasedonModelPredictiveStaticProgramming［J］.ActaAeronauticaetAstronauticaSinica，2021，42（11）：524912.（inChinese）

［10］NguyenNT，TranVN.OntheSolutionExistencetoConvexPo-lynomialProgramsandItsApplications［J］.OptimizationLetters，2021，15（2）：719-731.

［11］LiuXF，LuP.SolvingNonconvexOptimalControlProblemsbyConvexOptimization［J］.JournalofGuidance，Control，andDynamics，2014，37（3）：750-765.

［12］WangZB，GrantMJ.ConstrainedTrajectoryOptimizationforPlanetaryEntryviaSequentialConvexProgramming［J］.JournalofGuidance，Control，andDynamics，2017，40（10）：2603-2615.

［13］WangJB，CuiNG，WeiCZ.RapidTrajectoryOptimizationforHypersonicEntryUsingConvexOptimizationandPseudospectralMethod［J］.AircraftEngineeringandAerospaceTechnology，2019，91（4）：669-679.

［14］LiuXF，ShenZJ，LuP.ExactConvexRelaxationforOptimalFlightofAerodynamicallyControlledMissiles［J］.IEEETransactionsonAerospaceandElectronicSystems，2016，52（4）：1881-1892.

［15］LiuXF.Fuel-OptimalRocketLandingwithAerodynamicControls［J］.JournalofGuidance，Control，andDynamics，2018，42（1）：65-77.

［16］SaglianoM，MooijE.OptimalDrag-EnergyEntryGuidanceviaPseudospectralConvexOptimization［J］.AerospaceScienceandTechnology，2021，117：106946.

［17］YanBB，LiuRF，DaiP，etal.ARapidPenetrationTrajectoryOptimizationMethodforHypersonicVehicles［J］.InternationalJournalofAerospaceEngineering，2019，2019：1-11.

［18］ZhouX，ZhangHB，XieL，etal.AnImprovedSolutionMethodviathePole-TransformationProcessfortheMaximum-CrossrangeProblem［J］.ProceedingsoftheInstitutionofMechanicalEngineers，PartG：JournalofAerospaceEngineering，2020，234（9）：1491-1506.

［19］ZhouX，HeRZ，ZhangHB，etal.SequentialConvexProgrammingMethodUsingAdaptiveMeshRefinementforEntryTrajectoryPlanningProblem［J］.AerospaceScienceandTechnology，2021，109：106374.

［20］刘旭，叶松，林子瑞，等.火星大气进入轨迹伪谱凸优化设计方法［J］.宇航学报，2022，43（1）：71-80.

LiuXu，YeSong，LinZirui，etal.PseudospectralConvexProgrammingApproachforMarsAtmosphericEntryTrajectoryPlanning［J］.JournalofAstronautics，2022，43（1）：71-80.（inChinese）

［21］DomahidiA，ChuE，BoydS.ECOS：AnSOCPSolverforEmbeddedSystems［C］∥EuropeanControlConference（ECC），2013：3071-3076.

MidcourseGuidanceTrajectoryOptimizationofInterceptor

MissileBasedonSequentialConvexProgramming

LiJiong，ZhangJinlin*，ShaoLei，LiWanli，HeYangchao

（AirandMissileDefenseCollege，AirForceEngineeringUniversity，Xian710051，China）

Abstract：Aimingatthetrajectoryoptimizationproblemofinterceptormidcourseguidanceunderstrongnonlinearmulti-constraintconditions，atrajectoryoptimizationalgorithmforfixedtimeconstraintsisproposedbasedonsequentialconvexprogrammingmethodandcaptureregion.Sequentialconvexoptimizationmethodhashighcomputationalefficiencyforsolvingcomplexpolynomials.However，intrajectoryoptimizationproblems，thestrongnonlinearityofcontrolvariablesandtheconvergencedifficultyoffixedtimeterminalconstraintsaretwomaindifficulties.Firstly，theproblemistransformedintoanaffinesystembyusingaffinevariables，andtheaffinesystemisconvexizedanddiscretizedtosolvethenonlinearity.Then，aimingattheproblemthatterminalconstraintsaredifficulttoconvergeinafixedtime，aweightedrelaxationmethodofterminalconstraintsisproposedtotransformthemidcourseguidanceproblemintoasequenceconvexprogrammingproblem.Thesimulationresultsshowthattheproposedalgorithmcanquicklygeneratethemidcourseguidancetrajectoryofinterceptorthatmeetsmultipleconstraints.

Keywords：sequenceconvexprogramming；midcourseguidance；trajectoryoptimization；captureregion；multipleconstraints;hypersonic;interceptor

收稿日期：2022-05-30

基金項目：国家自然科学基金项目（62173339；61873278；61773398）

作者简介：李炯（1979-），男，安徽泾县人，博士，副教授。

*通信作者：张锦林（1997-），男，河南周口人，硕士研究生。