基于统一相场理论和内聚力模型的钢纤维混凝土界面过渡区力学性能研究
2023-05-30王辉明吴国政
王辉明 吴国政

摘 要:為探究数值模拟中界面过渡区不同建模方式对钢纤维混凝土力学性能及其损伤、破坏过程的影响,基于统一相场理论和内聚力模型,针对含单根钢纤维的混凝土拉伸试验,采用2种方法建立钢纤维混凝土界面过渡区的数值计算模型,对比分析不同建模方式对钢纤维混凝土力学性能及其破坏形态的影响,并考察不同因素对含单根钢纤维的混凝土极限抗拉强度的影响。结果表明,对混凝土基体部分采用相场断裂模型、界面过渡区采用内聚力模型,无论是计算结果还是细观破坏形态,都具有较好的准确性和可靠性;初始裂缝位置取30 mm和35 mm的钢纤维混凝土抗拉强度比取25 mm时分别提高30.8%和75.7%,钢纤维埋置角度为15°,30°和45°时的钢纤维混凝土抗拉强度比0°时分别降低12.2%,30.8%和48.9%,钢纤维增强作用受初始裂缝位置及钢纤维埋置角度影响较大,受钢纤维直径影响相对较小。采用统一相场理论可降低分析的难度、保证较高的计算精度,为研究钢纤维混凝土的损伤、断裂过程提供了理论参考。
关键词:复合建筑材料;界面过渡区;内聚力模型;统一相场理论;数值模拟
Study on mechanical properties of steel fiber reinforced concrete interface transition zone based on unified phase-field theory and cohesive zone model
WANG Huiming, WU Guozheng
(College of Architecture and Civil Engineering, Xinjiang University, Urumqi, Xinjiang 830017, China)
Abstract: In order to investigate the impact of different modeling methods of interface transition zone on the mechanical properties, damage and failure process of steel fiber reinforced concrete in numerical simulation, based on the unified phase-field theory and the cohesive zone model, two methods were used to establish a numerical calculation model of the interface transition zone of steel fiber reinforced concrete for the tensile test of concrete specimens containing a single steel fiber to compare and analyze the effects of different modeling methods on the mechanical properties and failure modes of steel fiber reinforced concrete, and the effects of different factors on the ultimate tensile strength of concrete containing a single steel fiber were investigated. The results show that the phase-field theory model for the matrix part and the cohesive zone model for the interface transition zone have good accuracy and reliability in both the calculation results and mesoscopic failure morphology; the tensile strength of steel fiber reinforced concrete with the initial crack location of 30 mm and 35 mm is 30.8% and 75.7% higher than that of 25 mm, respectively; the tensile strength of steel fiber reinforced concrete with the steel fiber embedding angle of 15°, 30°, and 45° is 12.2%, 30.8%, and 48.9% lower than that of 0°, respectively; the reinforcement effect of steel fiber is greatly influenced by the initial crack location and the embedding angle of steel fiber, and is relatively less influenced by the diameter of steel fiber. Adopting the unified phase-field theory can lower the analysis difficulty while guarantee higher computational accuracy, which provides theoretical reference for the study of the damage and fracture process of steel fiber reinforced concrete.
Keywords:composite building material; interfacial transition zone; cohesive zone model; unified phase-field theory; numerical simulation
混凝土材料具有较高的抗压强度和良好的耐久性,成为应用最为广泛的建筑工程材料。但随着时代和行业的发展,对工程材料提出了更高的要求,普通混凝土抗拉强度低、脆性大等缺陷使其应用受到了一定的限制[1]。在混凝土中掺入适量的乱向分布的钢纤维,可以明显改善普通混凝土抗拉强度低、脆性大等缺陷。钢纤维混凝土作为一种性能卓越的复合材料,不仅继承了普通混凝土抗压强度高的特性,而且钢纤维会抑制裂缝的扩展,使钢纤维混凝土构件在承载破坏时的延性和韧性都有显著增强,故钢纤维混凝土被越来越多地应用于大型建筑工程、道路桥梁以及隧道、大坝等重要的土木工程结构中[2-5]。
实践与研究表明,由于钢纤维与混凝土接触部分(即界面过渡区,interfacial transition zone,简称ITZ)仍是薄弱区域,使得钢纤维对混凝土增强增韧作用不能充分发挥。故界面作为钢纤维对混凝土发挥增强增韧作用的关键因素,研究其对钢纤维混凝土力学性能的影响至关重要。由于界面过渡区的复杂性及特殊性,试验研究具有一定的困难和局限性,故当前对其力学性能的研究仍相对缺乏和不够深入。已有大量学者通过数值模拟方法对钢纤维混凝土的力学性能进行了研究,XU等[6]建立骨料、钢纤维和水泥砂浆三相复合材料,通过对钢纤维混凝土试件的动态冲击试验进行数值模拟,研究了钢纤維混凝土的动态材料性能,但其并未考虑界面对宏观力学性能的影响。刘丰[7]通过结合MATLAB数学计算软件建立钢纤维混凝土二维模型,并模拟研究了钢纤维混凝土抗拉、抗压等基本力学性能指标,但其将钢纤维混凝土视为两相材料,未考虑界面对钢纤维混凝土力学性能的影响。程书怀等[8]建立二维钢纤维混凝土细观模型并对所建立的模型进行单轴拉伸模拟,采用双折线本构关系直接赋予界面的材料属性,其模拟结果与真实结果吻合良好,所建立的模型具有一定的可靠性。LIANG等[9]基于Delaunay三角剖分建立钢纤维混凝土三维细观模型,将钢纤维与砂浆部分分开建模,并通过滑动接触连接来反映界面的黏结滑移行为,所建立的模型可以以较高的计算效率和精度对钢纤维混凝土的力学性能进行模拟。兰晓芳[10]、HAN等[11]建立粗骨料、砂浆、钢纤维、骨料-砂浆界面及钢纤维-砂浆界面五相钢纤维混凝土复合材料,对界面部分采用双线性模型并直接赋予材料属性,通过扩展有限元方法模拟研究了钢纤维掺量以及钢纤维长度对钢纤维混凝土断裂特性的影响,数值模拟结果与试验结果吻合良好,验证了模型的可靠性。
利用数值模拟方法对钢纤维混凝土进行研究,选择合理适用的本构模型及破坏准则对混凝土基体的损伤破坏进行表征也至关重要。2017年,WU[12]基于热力学的理论框架,提出了统一相场理论并随之提出适用于准脆性材料的混凝土相场损伤模型,该模型对研究混凝土裂缝的产生、演化等过程提供了极大的便利且十分适用于模拟混凝土损伤破坏的情况。庄洛嘉[13]通过利用混凝土相场损伤模型对多个试验进行模拟,验证了混凝土相场损伤模型在混凝土破坏全过程仿真分析中的适用性。WU等[14]在此基础上探讨了混凝土相场损伤模型与扩展有限元方法对模拟混凝土非线性损伤破坏全过程的异同与优劣。YANG等[15]基于混凝土相场损伤模型,对素混凝土细观模型进行研究,证实了混凝土相场损伤模型在非均质材料中的可行性。考虑到混凝土相场损伤模型在混凝土损伤破坏数值模拟中的表现,本文所建立的钢纤维混凝土模型的混凝土基体部分采用该损伤模型表征。
综上,在对钢纤维混凝土进行数值模拟时,大部分学者对界面过渡区的处理都简单地采用了直接赋予材料属性的方式,该方法的可靠性、准确性还需进一步验证。本研究通过2种方式建立混凝土基体与钢纤维间薄弱的界面层,一是建立有厚度的界面层并采用与表征混凝土基体相同的混凝土相场损伤模型直接赋予材料属性,二是在混凝土基体与纤维之间嵌入一层零厚度的内聚力单元,在混凝土基体部分均采用混凝土相场损伤模型进行表征,利用数值模拟方法,对比分析界面过渡区不同建模方式对钢纤维混凝土力学性能及其细观破坏形态的影响。随后模拟了钢纤维混凝土试件在单轴拉伸荷载下的损伤过程,探究在不同因素下,钢纤维对混凝土增强增韧作用的影响,为钢纤维混凝土的损伤、断裂研究提供依据。
1 数值计算理论基础及控制方程
1.1 内聚力模型
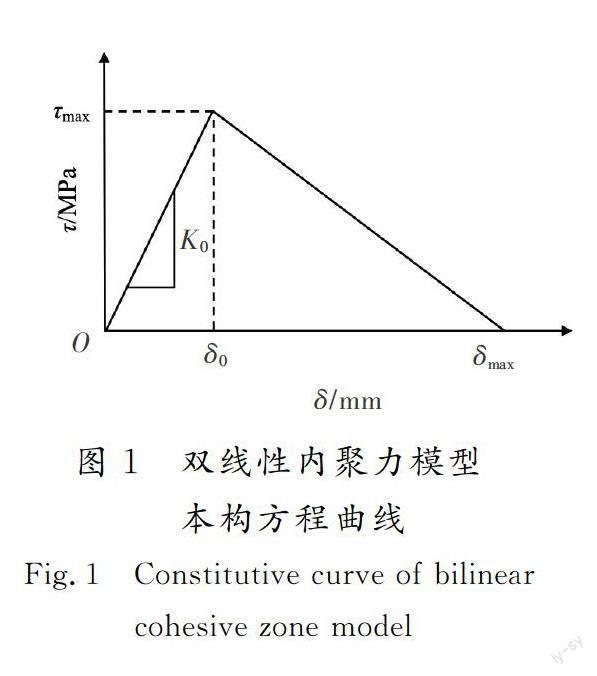
本文对模型界面的建模方式之一就是在钢纤维与混凝土基体间嵌入一层零厚度的内聚力单元,以此来模拟钢纤维与混凝土基体之间薄弱的界面层。内聚力单元作为一种功能性单元,处于2个相邻单元之间,合理的本构关系是准确、有效地描述界面损伤的关键。常用的内聚力模型有双线性、梯形、指数型以及多项式等形式[16],本文采用双线性内聚力模型。双线性内聚力模型是表征纤维与基体界面最有效、最常用的一种模型,其本构方程曲线如图1所示。
图1中,τmax为法向黏结强度,代表界面在分离前可以承受的最大法向黏结力;δmax为法向失效位移,代表可传递界面黏结力的最大法向的分离位移,当δ>δmax时,代表界面完全脱黏,两侧单元脱离;τ~δ曲线与横轴所交汇的面积即为界面断裂能GC;K0表示初始切向刚度。界面断裂能GC、黏结强度τ和失效位移δ作为内聚力模型的3个重要参数,三者之间的关系可表示为
双线性内聚力单元从损伤起始到损伤演化过程,都有各自的判定依据。损伤起始准则用于判定何时开始损伤和何时刚度开始衰减。本文中初始起始准则选用最大名义应力准则,起始损伤满足:
式中τ0n和τ0t分别表示法向和切向所能承受的最大应力值。
在发生初始损伤后,随即进入损伤演化过程。内聚力模型中的损伤演化准则用于表达分离位移和牵引力二者之间的关系,用刚度退化表征其力学性能的退化。损伤演化可表示为
式中D表示刚度退化,其取值范围为0~1。当D=0时,表示未产生损伤;当D=1时,表示完全损伤。损伤产生后,内聚力单元的切向刚度K衰减为
1.2 统一相场理论模型
为了更直观、准确地表征混凝土基体部分的损伤破坏,本文采用基于统一相场理论提出的混凝土相场损伤模型。统一相场理论的基本概念和控制方程[12,17-19]简述如下。
1.2.3 混凝土相场损伤模型
在统一相场损伤理论中有2个重要的特征函数,分别是用于对物理裂缝进行规范化拓扑的裂缝几何函数α(d)和反映材料软化过程的能量衰减函数ω(d)。WU等[12,17-19]将统一相场理论与内聚力模型进行结合,明确了裂纹几何函数α(d)和能量衰减函数ω(d)在实际应用中的建议取值,从而提出混凝土相场损伤模型,具体的建议形式如下:
当p和ai(i = 1, 2, 3)取特定值时,可以反映不同的应变软化准则。本文采用混凝土常用的Cornelissen软化准则,该准则根据混凝土相关试验数据标定关键参数,更适用于混凝土准脆性材料,其中p=2,a2=1.386 8,a3=0.656 7。
对于统一相场理论的具体数值实现,本文采用Fortran语言编程,利用ABAQUS有限元软件的用户子程序(UEL)功能[19],通过交替求解上述2个控制方程[20-21],实现对结构损伤与破坏的全过程模拟。
2 含单根钢纤维混凝土试件拉伸试验模型的建立及验证分析
2.1 模型建立
考察钢纤维与混凝土界面过渡区的宏观力学行为,不论是试验研究还是数值模拟,基本上都采用的是多种形式的单根钢纤维拉拔试验。本文参考文献[22]建立单纤维混凝土拉伸模型并进行数值模拟分析,模型及其尺寸如图3 a)所示,混凝土基体尺寸为50 mm×50 mm,纤维长度为10 mm、纤维直径为0.8 mm。
本文采用以下2种方法来建立、表示混凝土基体与钢纤维间的界面层: 1) 建立有厚度的界面层并采用与表征混凝土基体单元相同的混凝土相场损伤模型直接赋予材料属性;2) 在混凝土基体与纤维之间嵌入一层零厚度的内聚力单元。通过对这2种方式所建立模型的模拟结果进行对比分析,以确定合理的界面形式,所建立模型分别如图3 c)、图3 d)所示。已有相关研究表明[23-24],ITZ厚度一般取为10~50 μm,但网格过于密集会对数值计算造成困难,故在保证模拟结果准确性的前提下,大多数数值模拟中ITZ的厚度取0.1~0.8 mm[25],在本文研究中ITZ厚度取为0.5 mm。
本文所建立的单纤维混凝土细观力学模型由混凝土基体、钢纤维以及二者之间的界面层所组成。采用ABAQUS有限元软件对模型进行数值计算,混凝土基体及有厚度的界面层采用混凝土相场损伤模型,选用CPS4T单元(其是同时具有位移和温度自由度的4节点平面应力完全积分单元);假定钢纤维为线弹性,选用CPS4单元(该单元为4节点平面应力完全积分单元);将零厚度的内聚力单元嵌入混凝土基体与钢纤维之间以表示二者之间的界面黏结,零厚度的内聚力单元采用双线性内聚力模型,选用COH2D4单元(其为二维的内聚力单元)。模型中各相的材料参数参考文献[22]获取,材料参数如表1所示。对模型进行网格划分,如图3 b)所示,为提高计算效率,在裂缝潜在的区域内对网格进行加密处理(网格单元尺寸为0.25 mm),从而获得更接近于真实物理现象的裂缝损伤,而在其他区域稍作放大,有限元模型共划分为34 252个节点和34 043个单元。试件左侧受水平位移约束、上下两侧受竖向位移约束,加载方式采用位移加载,约束及加载位置如图3 a)所示。
2.2 模型验证及分析
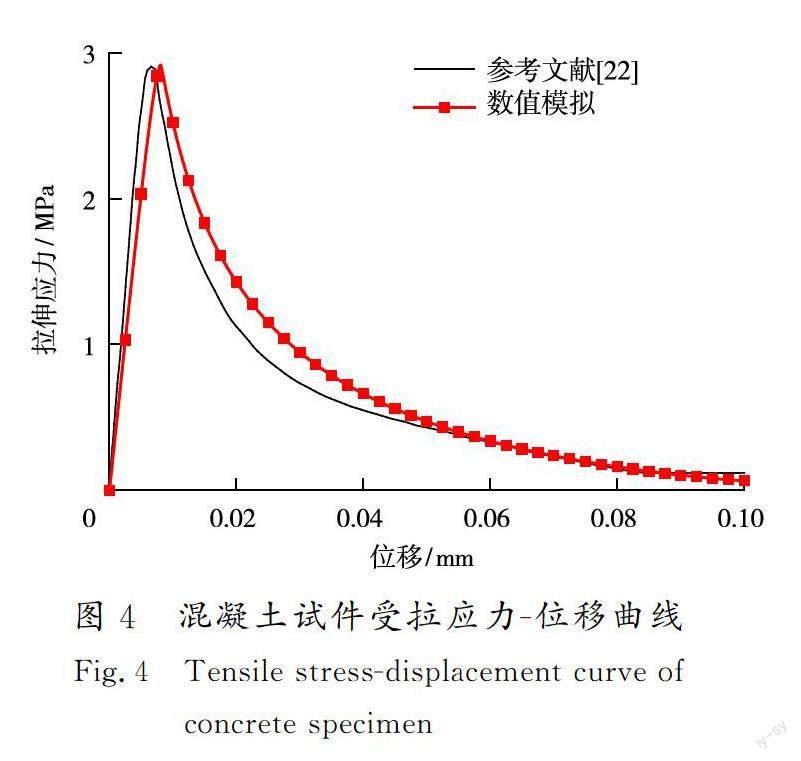
本文首先对基于统一相场理论的混凝土数值计算模型进行验证。图4为模拟素混凝土试件受拉所得到的应力-位移曲线与文献[22]中相应结果的对比,其中纵轴为试件所受的拉伸应力,横轴为对试件所施加的横向位移。模拟所得的峰值应力以及峰值应力所对应的位移分别为2.914 MPa和0.008 1 mm,對比文献[22]结果(2.903 MPa和0.006 6 mm),峰值应力误差仅为0.4%,且2条曲线吻合良好,表明混凝土相场损伤模型能够较为准确可靠地反映混凝土基体部分的损伤破坏情况。
其次,对采用内聚力模型的钢纤维混凝土数值计算模型进行验证,并与混凝土相场损伤模型进行比较,为此参考了文献[22],对2种工况进行考察。其中内聚力模型的参数通过参考文献[22]中的试验结果进行取值。
工况1:内聚力模型(CZM)中的零厚度界面黏结强度τ=0.3 MPa,断裂能GC=0.09 N/mm;相场损伤模型(PF-CZM)中的有厚度界面层的材料参数取值等同于砂浆基体,抗拉强度ft=2.3 MPa,断裂能GC=0.09 N/mm,模拟单纤维混凝土模型受拉所得的应力-位移曲线与文献[22]中结果的对比如图5 a)所示。其中内聚力模型模拟所得峰值应力为2.909 MPa,相场损伤模型模拟所得结果为2.906 MPa,对比文献[22]结果(2.908 MPa),三者之間峰值应力误差极小,可忽略不计,且3条曲线吻合良好。
工况2:内聚力模型(CZM)中的零厚度界面黏结强度τ=0.5 MPa,断裂能GC=0.09 N/mm;相场损伤模型(PF-CZM)中的有厚度界面层的抗拉强度ft=2.5 MPa,断裂能GC=0.09 N/mm,模拟单纤维混凝土模型受拉所得的应力-位移曲线与文献[22]中结果的对比如图5 b)所示。由图可知,模拟所得结果与文献[22]中结果吻合良好。结合2种工况可以看出,无论是采用零厚度界面的内聚力模型还是采用有厚度界面层的相场损伤模型,在数值模拟结果上都具有较好的准确性和可靠性。
图6展示了单纤维混凝土试件在拉伸作用下其内部裂缝的产生及扩展过程。对应工况1,零厚度界面内聚力模型的裂缝产生及扩展过程如图6 a)所示,此时界面强度相对较弱。由图6 a)可以发现,随着位移的增加,裂缝从缺口处萌生并逐渐朝着相对薄弱的界面扩展,并最终形成宏观裂缝从而导致试件失效,纤维被拔出(界面单元达到临界应力)。有厚度界面层的相场损伤模型的裂缝产生及扩展过程如图6 c)所示,通过对比可以发现,即使在界面强度较弱的情况下,采用有厚度界面模型模拟时,也体现不出纤维被拔出的破坏形式。也就是说采用零厚度的内聚力单元来模拟混凝土基体与钢纤维之间薄弱的界面层,模拟所得试件的细观破坏形态更加真实。
对应工况2,零厚度界面内聚力模型的裂缝产生及扩展过程如图6 b)所示,此时界面强度相对提高,纤维的存在使得裂缝绕开纤维所在位置,与工况1的裂缝形态略有不同,基体损伤破坏的范围更大,故试件拉伸软化应力较大;有厚度界面层的相场损伤模型的破坏形态与图6 c)所示形态相似,体现不出界面强度变化所带来的破坏形态的改变。运用内聚力单元模拟薄弱的界面层,其破坏形态随界面强度的变化而变化,更加符合真实的物理现象。
综上,在混凝土基体部分采用混凝土相场损伤模型,并在薄弱的界面层嵌入零厚度的内聚力单元采用双线性内聚力模型,无论是在数值上还是在细观破坏形态上,都具有较好的准确性和可靠性,故本文在数值模拟中均采用这2个模型对试件力学行为进行分析。
3 不同因素对单根钢纤维混凝土拉伸力学性能的影响
建立如图7所示的含单根钢纤维的钢纤维混凝土模型,模型尺寸如图7 a)所示。混凝土基体尺寸为30 mm×80 mm,钢纤维选用长度为35 mm、直径为0.8 mm的平直形钢纤维。在混凝土基体与钢纤维之间嵌入一层零厚度的内聚力单元以表示薄弱的界面层,如图7 b)所示。其他参数与上述工况2保持一致,针对不同初始裂缝位置、钢纤维角度以及钢纤维直径的单根钢纤维混凝土试件在单轴拉伸位移荷载下的破坏过程进行数值模拟,并分析这些因素对钢纤维混凝土极限抗拉强度的影响。
3.1 初始裂缝位置的影响
针对图7试件模型,初始裂缝位置l分别取25,30和35 mm,建立3种不同初始裂缝位置的有限元模型,并对钢纤维混凝土进行拉伸模拟,结果如图8所示。
由图8可以看出,随着初始裂缝位置l的增大,试件的极限抗拉强度也增大。l=30 mm和l=35 mm的钢纤维混凝土的峰值拉力比l=25 mm时分别提高了30.8%和75.7%,这也表明了初始裂缝与钢纤维的相对位置会显著影响钢纤维混凝土的极限抗拉强度。
图9展示了钢纤维混凝土试件在拉伸作用下裂缝的产生及扩展过程,由于界面强度相对较弱,3种情况下均表现出纤维拔出的破坏形式。但随着l的增大,初始裂缝位置远离钢纤维端部,钢纤维与混凝土基体的接触面积增大,钢纤维脱离混凝土基体所需的拉力增大,故试件的峰值拉力也相应增大。
3.2 钢纤维角度的影响
针对图7试件模型,钢纤维方向分别取θ=0°,15°,30°和45° 4种不同角度,建立相应的有限元模型,钢纤维长度35 mm及初始裂缝位置l=30 mm保持不变,并对钢纤维混凝土进行拉伸模拟,结果如图10所示。
由图10可以看出,随着钢纤维倾角θ的增大,试件的极限抗拉强度减小,钢纤维对试件的增强效果随之减小。θ为15°,30°和45°时的钢纤维混凝土的峰值拉力比θ为0°时分别降低了12.2%,30.8%和48.9%,由此可知,钢纤维埋置角度的大小即裂缝扩展方向与钢纤维夹角对钢纤维混凝土的极限抗拉强度影响较为明显。
3.3 钢纤维直径的影响
针对图7试件模型,分别建立钢纤维直径为0.6,0.8和1.0 mm的有限元模型,钢纤维长度35 mm及初始裂缝位置l=30 mm保持不变,并对钢纤维混凝土进行拉伸模拟,结果如图11所示。
由图11可以看出,随着钢纤维直径的增大,试件的极限抗拉强度增大。钢纤维直径为0.8和1.0 mm的钢纤维混凝土的峰值拉力比钢纤维直径为0.6 mm时分别提高了0.6%和0.9%,表明钢纤维直径的大小对钢纤维混凝土的极限抗拉强度影响相比于上述2个因素相对较弱。
4 结 论
基于统一相场理论及内聚力模型对含单根钢纤维的混凝土拉伸试验进行模拟,对比分析界面过渡区不同建模方式对钢纤维混凝土力学性能及其损伤破坏形态的影响。与已发表的相关数值模拟工作相比,本文采用了最新提出的统一相场理论,在表征混凝土材料时具有数值实现简单、网格敏感性小、能够保证很高的计算精度等优点,而且可以直观地观察到钢纤维对裂缝的阻碍作用,同时探究不同因素对钢纤维混凝土极限抗拉强度的影响。主要结论如下。
1)通过对界面过渡区不同处理方式的单纤维混凝土试件受拉的数值模拟结果及其破坏形态的对比分析可以发现,在混凝土基体部分采用相场损伤模型、在界面过渡区嵌入零厚度的内聚力单元,是对钢纤维混凝土较优的数值建模方式,无论是在数值模拟结果上还是在细观破坏形态上,都具有较好的准确性和可靠性。
2)通过研究不同因素对单根钢纤维混凝土拉伸力学性能的影响发现,当初始裂缝位置l取30和35 mm的钢纤维混凝土的抗拉强度比取25 mm时分别提高了30.8%和75.7%,钢纤维角度θ取15°,30°和45°时的钢纤维混凝土的抗拉强度比取0°时分别降低了12.2%,30.8%和48.9%,故钢纤维的增强作用受初始裂缝位置以及裂缝扩展路径的影响较大,当裂縫距钢纤维端部较远且裂尖方向与钢纤维夹角较大时,钢纤维的增强作用更明显。反之,钢纤维对混凝土的增强效果较差,甚至会降低混凝土的强度。
3)通过探究钢纤维直径对单根钢纤维混凝土拉伸力学性能的影响发现,钢纤维直径为0.8和1.0 mm的钢纤维混凝土的抗拉强度比钢纤维直径为0.6 mm时分别提高了0.6%和0.9%,表明随着钢纤维直径的增大,试件的极限抗拉强度增大。当钢纤维直径增大时,钢纤维与混凝土基体间接触面积增大,故增大钢纤维的直径有利于提高钢纤维与混凝土基体之间的黏结性能,从而提高钢纤维混凝土的力学性能,但相较于本文其他2个因素对钢纤维混凝土的增强效果相对较差。
本文仅针对钢纤维混凝土二维有限元模型进行了数值模拟,而三维有限元模型的真实性及可靠性更强,因此,未来拟基于统一相场理论对三维条件下的细观结构进行数值模拟研究。
参考文献/References:
[1] 袁勇,邵晓芸.合成纤维增强混凝土的发展前景[J].混凝土,2000(12):3-7.
YUAN Yong,SHAO Xiaoyun.Prospect of synthetic fiber reinforced concrete[J].Concrete,2000(12):3-7.
[2] GILBERT R I,BERNARD E S.Post-cracking ductility of fibre reinforced concrete linings in combined bending and compression[J].Tunnelling and Underground Space Technology,2018,76:1-9.
[3] ABBAS Y M,KHAN M I.Fiber-matrix interactions in fiber-reinforced concrete:A review[J].Arabian Journal for Science and Engineering,2016,41(4):1183-1198.
[4] ISLAM S M,HUSSAIN R R,MORSHED M A Z.Fiber-reinforced concrete incorporating locally available natural fibers in normal- and high-strength concrete and a performance analysis with steel fiber-reinforced composite concrete[J].Journal of Composite Materials,2012,46(1):111-122.
[5] de SMEDT M,VRIJDAGHS R,van STEEN C,et al.Damage analysis in steel fibre reinforced concrete under monotonic and cyclic bending by means of acoustic emission monitoring[J].Cement and Concrete Composites,2020,114.DOI: 10.1016/j.cemconcomp.2020.103765.
[6] XU Z,HAO H,LI H N.Mesoscale modelling of fibre reinforced concrete material under compressive impact loading[J].Construction and Building Materials,2012,26(1):274-288.
[7] 刘丰.钢纤维混凝土细观层次数值模拟研究[D].广州:华南理工大学,2014.
LIU Feng.Study of Numerical Simulation for Steel Fiber Reinforced Concrete on Meso-level[D].Guangzhou:South China University of Technology,2014.
[8] 程书怀,任志刚,余细东,等.钢纤维混凝土细观二维建模与数值研究[J].武汉理工大学学报,2015,37(3):69-74.
CHENG Shuhuai,REN Zhigang,YU Xidong,et al.Two-dimensional mesoscale modelling and numerical analysis of steel fibre reinforced concrete[J].Journal of Wuhan University of Technology,2015,37(3):69-74.
[9] LIANG Xiangwei,WU Chengqing.Meso-scale modelling of steel fibre reinforced concrete with high strength[J].Construction and Building Materials,2018,165:187-198.
[10]蘭晓芳.基于扩展有限元的钢纤维混凝土断裂破坏数值研究[D].郑州:郑州大学,2019.
LAN Xiaofang.Numerical Study on Fracture Damage of Steel Fiber Reinforced Concrete Based on Extended Finite Element Method[D].Zhengzhou:Zhengzhou University,2019.
[11]HAN Juhong,ZHAO Mengmeng,CHEN Jingyu,et al.Effects of steel fiber length and coarse aggregate maximum size on mechanical properties of steel fiber reinforced concrete[J].Construction and Building Materials,2019,209:577-591.
[12]WU Jianying.A geometrically regularized gradient-damage model with energetic equivalence[J].Computer Methods in Applied Mechanics and Engineering,2018,328:612-637.
[13]庄洛嘉.基于统一相场损伤理论的混凝土破坏全过程分析应用研究[D].广州:华南理工大学,2019.
ZHUANG Luojia.Application Study of Unified Phase Field Theory for Modeling Localized Failure in Concrete[D].Guangzhou:South China University of Technology,2019.
[14]WU Jianying,QIU Jiefeng,NGUYEN V P,et al.Computational modeling of localized failure in solids:XFEMvs PF-CZM[J].Computer Methods in Applied Mechanics and Engineering,2019,345:618-643.
[15]YANG Zhenjun,LI Beibei,WU Jianying.X-ray computed tomography images based phase-field modeling of mesoscopic failure in concrete[J].Engineering Fracture Mechanics,2019,208:151-170.
[16]卢子兴.复合材料界面的内聚力模型及其应用[J].固体力学学报,2015,36(sup1):85-94.
LU Zixing.A simple review for cohesive zone models of composite interface and their applications[J].Chinese Journal of Solid Mechanics,2015,36(sup1):85-94.
[17]WU Jianying.A unified phase-field theory for the mechanics of damage and quasi-brittle failure[J].Journal of the Mechanics and Physics of Solids,2017,103:72-99.
[18]WU Jianying,NGUYEN V P.A length scale insensitive phase-field damage model for brittle fracture[J].Journal of the Mechanics and Physics of Solids,2018,119:20-42.
[19]WU Jianying,HUANG Yuli.Comprehensive implementations of phase-field damage models in Abaqus[J].Theoretical and Applied Fracture Mechanics,2020,106.DOI: 10.1016/j.tafmec.2019.102440.
[20]BOURDIN B,FRANCFORT G A,MARIGO J J.Numerical experiments in revisited brittle fracture[J].Journal of the Mechanics and Physics of Solids,2000,48(4):797-826.
[21]BOURDIN B,FRANCFORT G A,MARIGO J J.The Variational Approach to Fracture[M].Dordrecht:Springer,2008.
[22]ZHANG H,HUANG Y J,YANG Z J,et al.A discrete-continuum coupled finite element modelling approach for fibre reinforced concrete[J].Cement and Concrete Research,2018,106:130-143.
[23]TASONG W A,LYNSDALE C J,CRIPPS J C.Aggregate-cement paste interface(Part I):Influence of aggregate geochemistry[J].Cement and Concrete Research,1999,29(7):1019-1025.
[24]XIAO Jianzhuang,LI Wengui,CORR D J,et al.Effects of interfacial transition zones on the stress-strain behavior of modeled recycled aggregate concrete[J].Cement and Concrete Research,2013,52:82-99.
[25]KIM S M,ABU AL-RUB R K.Meso-scale computational modeling of the plastic-damage response of cementitious composites[J].Cement and Concrete Research,2011,41(3):339-358.
