基于学习路径分析的“平均数”单元整体教学
2023-05-30刘贤虎章勤琼
刘贤虎 章勤琼

【摘 要】平均數这一学习单元的核心目标是理解平均数的意义以及感悟平均数的特性。平均数作为重要的代表量,其描述功能是建立在“代表”的意义之上的,即用于刻画一组数据的集中程度,表达总体的集中状况,在此基础上,让学生深刻理解平均数概念并进行运用。基于以上理解,教师对“平均数”的单元目标和学生起点进行分析,并设计了相应的学习路径与学习任务。
【关键词】学习路径;平均数;代表量;统计
“统计与概率”是义务教育阶段数学学习的重要领域之一,在小学阶段包括“数据分类”“数据的收集、整理与表达”和“随机现象发生的可能性”三个主题。其中“数据的收集、整理与表达”包括数据的收集和用统计图表、平均数、百分数表达数据。借助生活中大量数据蕴含着的有价值的信息,利用统计图表和统计量呈现和刻画这些信息,让学生形成初步的数据意识,是《义务教育数学课程标准(2022年版)》一以贯之的教学要求。
具体到平均数,它是小学阶段要学习的两个重要统计量中的一个。如何帮助学生建立对平均数的认识,凸显其作为统计量的描述功能,实现学生对平均数的理解?下面,笔者基于对学习路径的分析,对“平均数”这一学习单元进行整体思考和把握。
一、理解单元目标
(一)单元内容概述
平均数在北师大版教材和人教版教材中都不是单独的单元,而是与条形统计图等内容混合编排。下面将平均数作为一个学习单元进行对比分析。人教版教材只在四年级下册集中编排平均数,将平均数和复式条形统计图整合为一个单元。其中平均数部分的内容包括平均数的意义和求法、用平均数比较两组数据的总体情况。北师大版教材把平均数分为两个部分,其中四年级下册第6单元“数据的表示和分析”将条形统计图、折线统计图和平均数编排在一起,安排的是认识平均数,五年级下册第8单元“数据的表示和分析”将复式条形统计图与平均数编排在一起,安排的是进一步认识平均数,体会平均数的实际意义。具体教学目标如下。
人教版教材:体会平均数的作用,能计算平均数,能用自己的语言解释其实际意义。
北师大版教材:了解平均数的意义,会求简单数据的平均数(结果为整数),能解决简单的实际问题。进一步认识平均数,体会平均数的实际应用,感受数学与日常生活的密切联系。
综上所述,平均数的学习内容和要求主要有三个:理解平均数的意义;掌握计算平均数的方法;体会平均数的实际应用。
(二)单元核心目标
本单元核心目标是理解平均数的意义以及感悟平均数的特性。
首先,平均数作为统计量,同时具备描述功能和推断功能,在小学阶段以描述功能的学习为主,而平均数最重要的描述功能是代表性,是描述一组数据整体水平的良好代表量。“平均数教学要引导学生在熟悉的情境中理解平均数所具有的代表性,通过刻画一组数据的集中程度表达总体的集中状况。”因此,只有理解了平均数的代表作用,学生才能真正理解平均数的意义。
其次,是感悟平均数的特性,包括代表性、虚拟性、敏感性、区间性、公平性等。
以上目标都与平均数的“代表性”密切相关。
(三)核心目标具体化
结合以上分析,将核心目标具体化为两点。一是理解平均数的意义。其主要内涵包含三个水平层次:认识代表量,会用一个数(总数、最高值、平均数等)代表一组数据的水平;会计算平均数,能运用移多补少或求和均分等方法;能用语言准确描述平均数是一组数据整体水平的代表量。二是感悟平均数的特性。具体包括:代表性,平均数代表一组数据的集中趋势;虚拟性,感受平均数不是实际的值,是均分出来的;敏感性,平均数受每个数据的影响;区间性,平均数介于最大值和最小值之间;公平性,平均数是“移多补少”“求和均分”得到的数。
二、确定学习起点
学生有一定的认知基础,在第一学段已经理解了平均分及除法运算含义。“平均分”和平均数的意义不同,但计算方法一样,学生掌握计算方法相对容易。学生也有相关经验,如以往的期末考试后,教师会介绍班级的平均分。
四年级学生的统计意识比较薄弱,其生活经验相对肤浅。用统计的意义去理解“平均数”需要有一定的统计意识和一定的生活经验,由于这两方面的不足,影响了学生对“平均数”意义的理解。
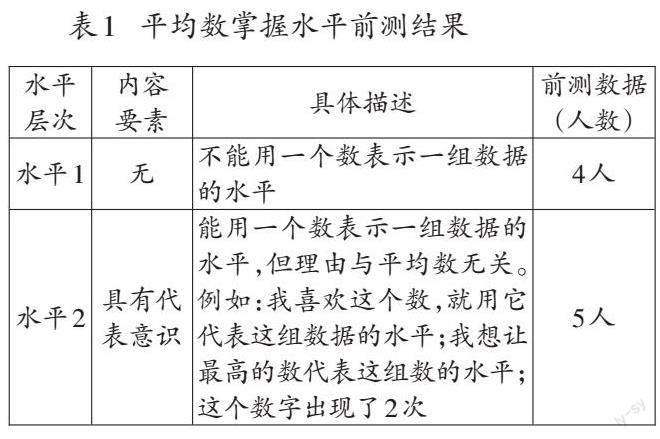
为此,笔者试图通过前测对上述情况作进一步的了解。前测主要针对核心目标中的“理解平均数的意义”这一内容,并根据理解平均数的意义的具体目标,制订评价框架,划定水平层次,再设计相应的测试题。“如果学习素材研究的数据采用的是一个个体的多次水平,这样的数据便于在推断的时候用,如下一次可能有几个。而在对整体数据的水平描述上,比较合适的是采用一个群体的横向的数据,而不是一个个体的纵向的数据。”因此,笔者在前测中采用了冬奥会滑雪比赛中不同评委打分的情境。前测题如下所示。
1.苏翊鸣在单板滑雪男子大跳台决赛的第二跳,4个评委打分:93、93、94、92。你认为应该用多少表示这一跳的成绩?说说你的理由。
2.苏翊鸣在决赛中的第一跳,4个评委打分:89、89、90、90。你认为应该用多少表示这一跳的成绩?说说你的理由。
3.哪一跳的成绩更好?写出你是怎么比较的。
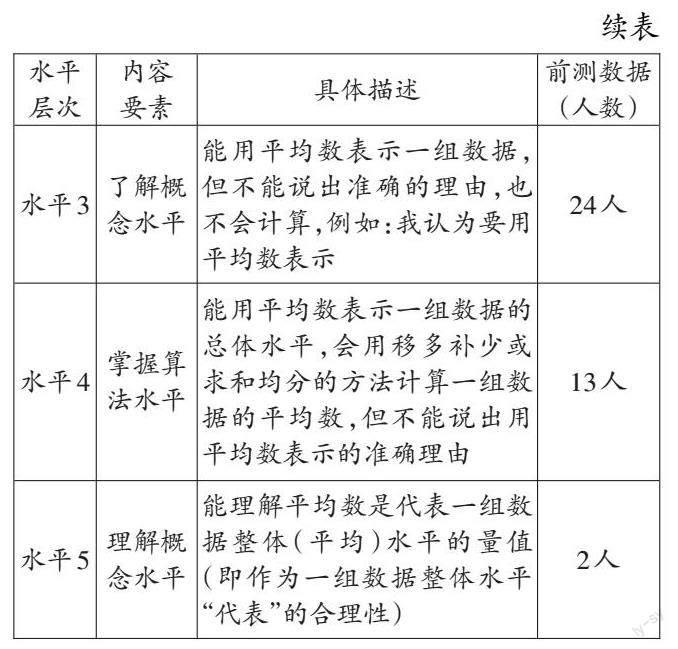
测试题中的第1题、第2题评价学生是否具有代表意识,会用什么数来代表。如果学生选择用平均数来代表,是否会计算。第3题根据学生选择的比较方式,如比最高分、平均数、第二跳的最低分与第一跳的最高分或一个一个数比等,及其描述的理由,评价学生是否理解平均数的概念意义。以下是前测结果(如表1)。
从前测结果看出,学生具有一定的“代表”意识,对平均数这个概念有一定的了解,接近25%的学生会求平均数,但绝大多数学生不能理解“平均数”这个概念的意义。
因此,对数据“代表”意识的已有观念和利用平均分的认知基础是学生研究平均数的学习起点;对平均数能代表一组数据整体水平的认识和选择合适代表量是学生的学习难点。
三、分析學习路径
基于以上分析,笔者对“平均数”的学习路径做了相应的调整与优化。
首先,认识代表量和平均数。借助比赛中不同评委打分的现实情境,让学生感受数据,读懂数据,初步理解数据。接着让学生尝试画出数据,进行数据表达,进一步思考如何用一个数描述比赛成绩。有了直观的感受,借助已有经验,学生会想到用最高分、总分、出现次数最多的分数、平均分等来代表。最后让他们借助代表量进行判断(如图1)。在此过程中,学生初步认识平均数是一组数据整体水平的良好代表量,学会用移多补少、求和均分等方法计算平均数。
其次,理解平均数的意义和特性。通过比较两组个数不同的数据,让学生进一步理解平均数是代表一组数据整体水平的良好代表量,同时体会平均数的虚拟性、区间性、敏感性和公平性,最后进行合理推断,进而解决问题(如图2)。
四、单元整体教学的思考
笔者以人教版教材为基础,从单元整体的视角出发,对平均数的教学做出适当调整,将平均数教学分为两节课,重点关注平均数的描述功能,适当涉及平均数的推断功能。
1.将“代表量”作为理解平均数的着力点。学生接触统计时最先思考的是代表量,“代表”是理解平均数意义的重要基础,“代表性”也是平均数最重要的特性。人教版教材例1中“求平均每人收集了多少个矿泉水瓶”强调求平均数的方法,不明确是反映“描述”还是“预测”的统计意义。因此,笔者转而将苏翊鸣决赛中第二跳和第一跳的评委打分作为学习素材,让学生用一个数表示这两跳的成绩。具体而言,先让学生以一个实际存在的样本来代表整体水平,在充分理解了这个层次的“代表”之后,再去理解实际存在的样本都不是整体水平的平均数,而需要以一个计算出来的数值来代表平均水平的情况。如此教学,凸显平均数的描述功能,更符合学生理解平均数的认知规律。
2.将数据理解和数据表达有效结合。解决人教版教材例2中的“踢毽比赛中男、女生队哪个队的成绩好”这一问题时,要让学生先理解数据。数据个数相同时,可以选择不同的代表量进行比较;数据个数不同时,平均数成为代表一组数据总体水平的良好代表量。学生充分经历数据理解的过程,自然决定选择平均数进行数据表达,深刻理解平均数的代表性。接着引导学生思考:“增加一名女生,成绩一定好吗?”学生认识到增加一个不同大小的数据带给整体水平的变化,感悟平均数的敏感性。最后让学生通过该女生前5次的成绩预测下一次的次数,再一次理解数据,进行数据表达,同时感受平均数的推断功能。
以下为每课时的学习目标、学习任务与实施要点(如表2)。
参考文献:
[1]章勤琼.计算平均成绩是否合适:小学阶段统计量教学的一些思考[J].教学月刊·小学版(数学),2020(1/2):95-98.
(1.广东省东莞松山湖中心小学
2.福建师范大学教育学院)
