反复有常——生活中的反比例

陈熙嫄

可以用反比例函数模型刻画的生活现象常因现实问题中“非负数”的限制而导致相关问题对应的都是双曲线在第一象限的情形——因变量随着自变量的增大而减小、随着自变量的减小而增大，简直就是“反复无常”.但只要掌握了反比例函数的性质，“无常”变“有常”也是易事，下面一起欣赏3例.

一、表格“单打”

例1（2022·湖南）科技小组为了验证某电路的电压U（V）、电流I（A）、电阻R（Ω）三者之间的关系：I=U/R，测得数据如下：

R/Ω 100 200 220 400

I/A 2.2 1.1 1 0.55

那么，当电阻R=55Ω时，电流I=_____A.

解析：表格法呈现的函数关系对应数值准确明晰，但不利于计算表格内尚未包含的自变量或因变量的值.因此，需要借助表格内自变量与因变量的对应关系求出函数解析式.把R=220，I=1代入I=U/R得：1= U/220，解得U=220，∴I=220/R，把R=55代入I=220/R得：I=220/55=4，故填4.

点评：函数关系有三种基本形式，要善于识别并因势、因需灵活转换才行.本题是一道简单的反比例函数应用题，题目给出的“I=U/R”即锁定了I与R之间的反比例关系，由表格数据求出反比例函数的解析式，再代入求值即可. 小技巧：选取计算量小的一对自变量和因变量数值进行计算.

二、图象“单打”

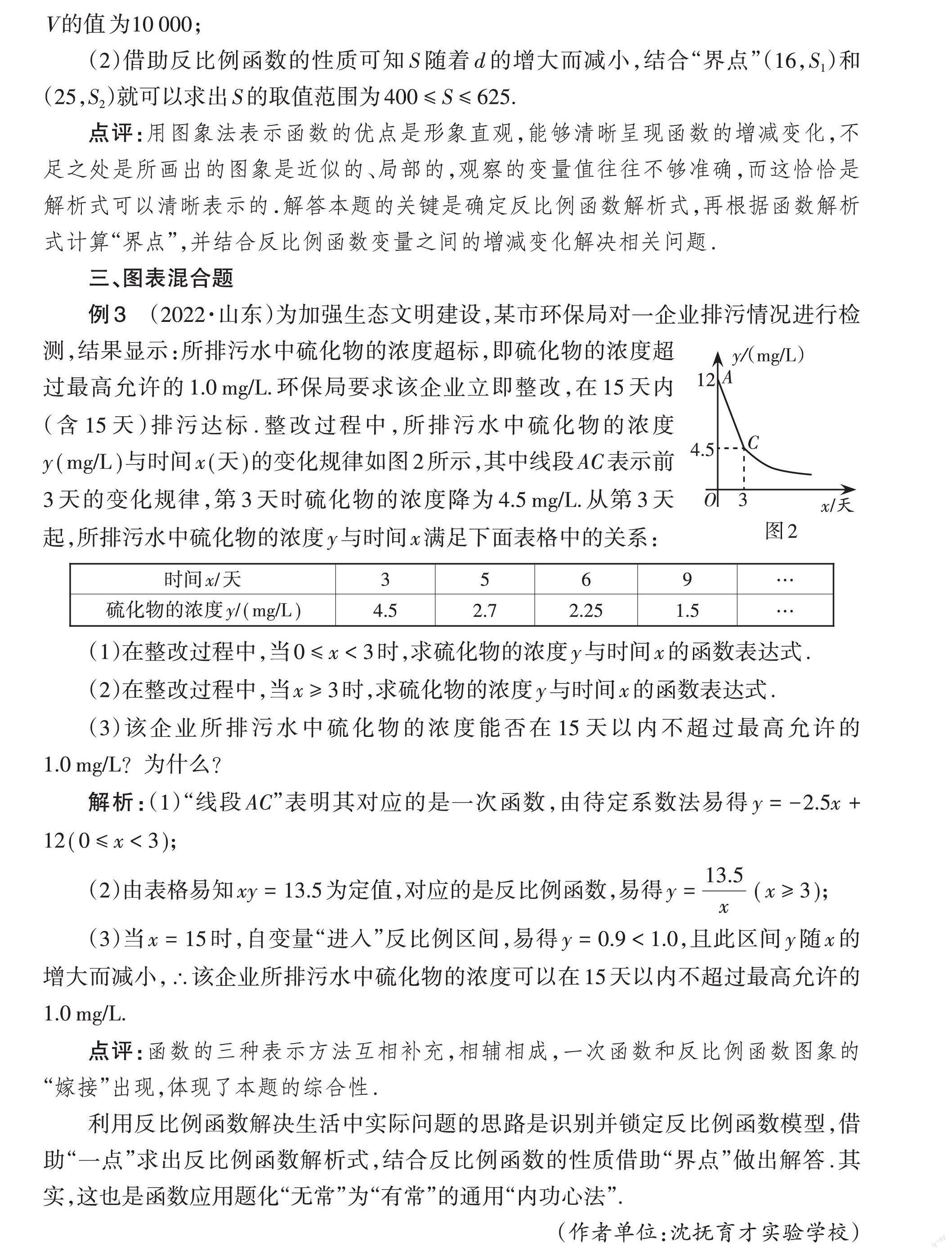
例2（2022·广东）某燃气公司计划在地下修建一个容积为V（V为定值，单位：m3）的圆柱形天然气储存室，储存室的底面积S（单位：m2）与其深度d（单位：m）是反比例函数关系，它的图象如图所示.

（1）求储存室的容积V的值；

（2）受地形条件限制，储存室的深度d需要满足16≤d≤25，求储存室的底面积S的取值范围.

解析：用图象法表示函数的优点是形象直观，能够清晰呈现函数的增减变化，不足之处是所画出的图象是近似的、局部的，观察的变量值往往不够准确，而这恰恰是解析式可以清晰表示的.

（1）设解析式为S=V/d，只需借助“一点”（20，500）即可求出V的值为10000（m^3）；

（2）借助反比例函数的性质因变量S随着自变量d的增大而减小，并结合“界点”（16，S1）和（25，S2）就可以求出S的范围为400≤S≤625.

点评：通过函数关系把三种表示方法结合起来，扬长避短，优势互补.解答本题的关键是确定反比例函数解析式，再根据函数解析式，计算“界点”，并结合反比例函数变量之间的增减变化解决相关问题.

三、图表“混双”

例3（2022·山东）为加强生态文明建设，某市环保局对一企业排污情况进行检测，结果显示：所排污水中硫化物的浓度超标，即硫化物的浓度超过最高允许的1.0mg/L.环保局要求该企业立即整改，在15天内（含15天）排污达标.整改过程中，所排污水中硫化物的浓度y（mg/L）与时间x（天）的变化规律如图所示，其中线段AC表示前3天的变化规律，第3天时硫化物的浓度降为4.5mg/L.从第3天起，所排污水中硫化物的浓度y与时间x满足下面表格中的关系：

时间x/天 3 5 6 9 …

硫化物的浓度y/（mg/L） 4.5 2.7 2.25 1.5 …

（1）在整改过程中，当0≤x<3时，硫化物的浓度y与时间x的函数表达式；

（2）在整改过程中，当x≥3时，硫化物的浓度y与时间x的函数表达式；

（3）该企业所排污水中硫化物的浓度能否在15天以内不超过最高允许的1.0mg/L？为什么？

解析：函数的三种表示方法互相补充，相辅相成，一次函数和反比例函数图象的“嫁接”出现，体现了本题的综合性.

（1）“线段AC”表明其对应的是一次函数，由待定系数法易得y=-2.5x+12（0≤x<3）；

（2）由表格易知x⋅y=13.5为定值，对应的是反比例函数，易得y=13.5/x（x≥3）；

（3）當x=15时，自变量“进入”反比例区间，易得y=0.9<1.0，且此区间y随x的增大而减小，∴该企业所排污水中硫化物的浓度可以在15天以内不超过最高允许的1.0mg/L.

点评：本题的第一道“待越龙门”是从函数的图象和表格中提取信息逆向判断函数类型，进而求函数解析式；第二道“待越龙门”是因自变量“分段”对应不同的函数关系，需要判断自变量所在区间，提高了综合性；第三道“待越龙门”是反比例函数的性质运用.题目的综合性塑造了作答者的“神勇无敌”！

利用反比例函数解决生活中实际问题的思路是识别并锁定反比例函数模型，借助“一点”求出反比例函数解析式，结合反比例函数的性质借助“界点”做出解答.其实，这也是函数应用题化“无常”为“有常”的通用“内功心法”.

（作者单位：沈抚育才实验学校）