基于贝叶斯网络的高压断路器拒动故障概率预测
2023-05-29马宏明钱国超王欣段雨廷李昭
马宏明,钱国超,王欣,段雨廷,李昭
(1. 云南电网有限责任公司电力科学研究院,云南 昆明 650217;2. 云南电网有限责任公司,云南 昆明 650011)
0 前言
高压断路器是构成电力系统的关键设备,数量众多,肩负着控制和保护的双重职能,其运行的安全稳定性直接影响电力系统的稳定。但现场应用中,高压断路器由于电气因素或机械因素的影响,往往会出现拒动故障,拒动会造成送电时间延长或造成越级跳闸、扩大事故和停电范围,甚至会引起系统解列。
高压断路器拒动基本都是由于单一元器件失效导致的[1-2]。但是由于有效的现场检测手段缺失,高压断路器的单一元器件运行状态难以直接评估。很多学者将设备整体性能试验数据、运维数据,运用数据挖掘技术提出了高压断路器状态综合评价方法。如贝叶斯法[3-9]、支持向量机法[10-11]和自适应算法[12]等。这些方法对指导高压断路器设备维护实践具有重要指导作用。同时,近几年来利用贝叶斯网络进行变电一次设备故障概率预测方法也引起了国内外学者的关注[13-20],但对高压断路器拒动概率进行预测的研究则少见报道。
实践证明,单一元器件失效的发生与产品质量、运行年限、运维水平等影响因素存在一定联系,运维单位掌握完整的设备信息、运维信息,只是信息量相对有限。高压断路器拒动为小概率事件,供决策用数据相对较少,在不具备大量数据的情况下处理拒动概率问题,贝叶斯概率决策理论具有明显优越性。
本文提出了基于贝叶斯网络的高压断路器拒动故障概率预测方法,采用贝叶斯概率理论,建立“影响因素—元器件—拒动”的多层贝叶斯网络,预测每台高压断路器的拒动概率,针对拒动概率较高断路器,提出差异化运维方法,降低全网断路器拒动风险,扭转高压断路器拒动风险被动防控的局面。
1 预测方法概述
建立产品质量、运行年限、运维水平等影响因素与单一元器件之间的关联关系,采用贝叶斯方法,通过影响因素修正单一元器件的故障率,再根据“或门”函数(任一元器件损坏均会导致拒动),确定顶层拒动概率;即基于拒动故障树建立“影响因素—元器件—拒动”的多层贝叶斯网络,预测每台高压断路器的故障率;最后通过历史数据验证模型的正确性(如图1)。
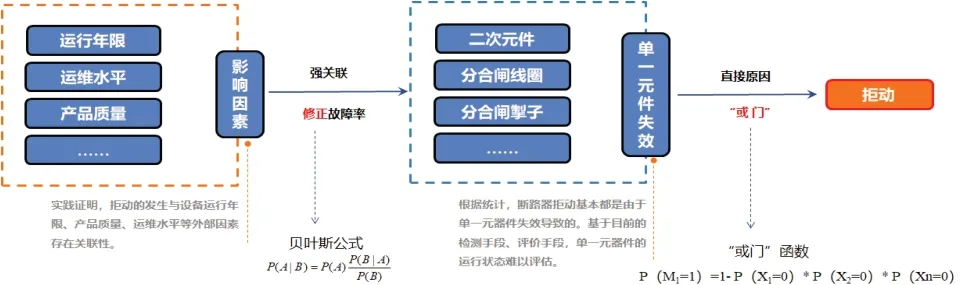
图1 预测方法思路
1.1 贝叶斯函数
通过贝叶斯理论,可以解决不具备大量数据的情况下处理概率问题,其整体思路为:先确定一个适当的预测值,在这个前提下观察实际发生的事件,再去逐次修正最初的判断。
因此贝叶斯可以分为3个部分,先验概率、似然函数和后验概率。
1)先验概率
我们把P(A)称为“先验概率”(Prior probability),先验概率是根据以往经验和分析得到的概率,本模型中系统最底层各节点先验概率P(Xi)已确定。
3)后验概率
P(A|B)称 为“后 验 概 率”(Posterior probability),贝叶斯公式通过似然函数不断调整先验概率得到后验概率,即在B事件发生之后,对A事件概率的重新评估。本模型中不同影响因素Yn影响下系统最底层各节点概率不断得到修正,使得预测结果逐步趋于准确。
1.2 “或门”函数
任一元器件损坏都会发生拒动故障,元器件与拒动之间通过“或门”连接。顶层事件“拒动T”的发生概率为:
2 模型构建
2.1 故障树建立
为“全方位、全领域、全要素”的查找高压开关拒动的影响因素,结合设备结构、原理及缺陷/事件原因统计分析,从电气故障和机械故障角度出发,梳理出不同电压等级、不同操动机构高压断路器拒动元器件故障树,其中110 kV电压等级弹簧操作机构拒动故障树如图2所示。
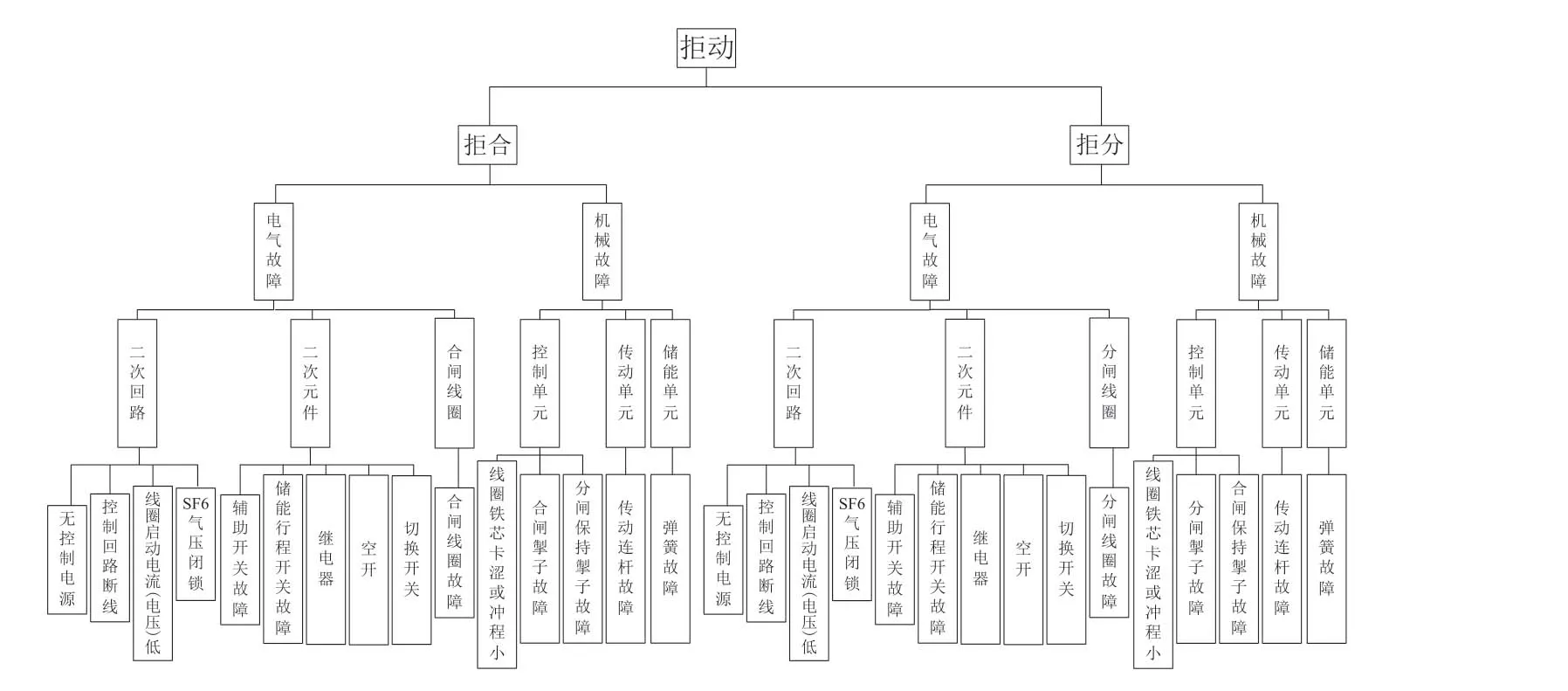
图2 110 kV电压等级弹簧操作机构拒动故障树
为便于模型分析,可将上述故障树简化如图3所示,由于无法直接获取每台高压断路器的元器件状态,即无法采用上述故障树进行每台高压断路器拒动概率预测。但影响因素Yn(控制回路配置、高缺陷设备型号、投运年限、机构类型、运维水平等)与高压断路器的元器件状态Xi存在着密切关联。

图3 简化后的高压断路器拒动故障树
因此可通过建立影响因素Yn与元器件Xi关联,间接评估元器件Xi状态。
2.2 贝叶斯网络建立
2.2.1 影响因素Yn与元器件Xi的关联分析
对底层节点Xi与影响因素Yn关联性进行系统分析:
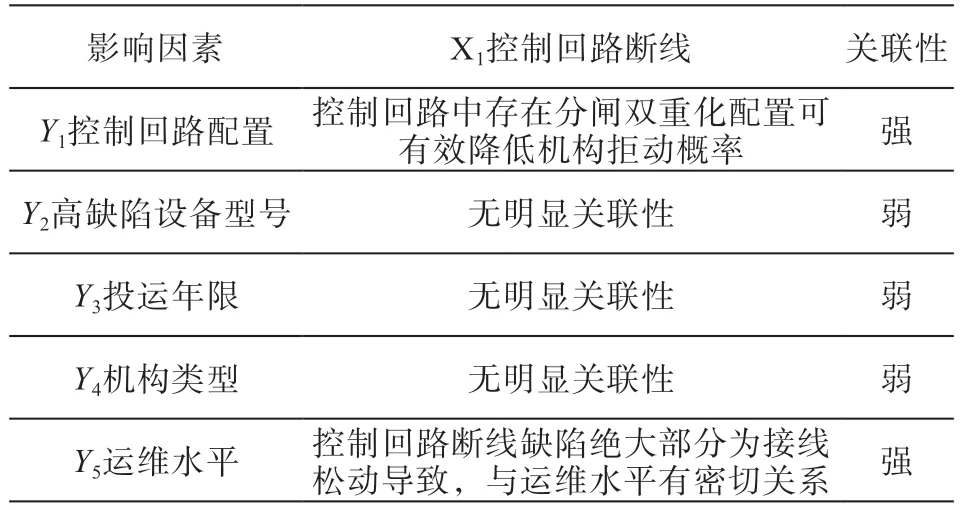
表1 底层节点X1与影响因素Yn关联性分析

表2 底层节点X2与影响因素Yn关联性分析

表4 底层节点X4与影响因素Yn关联性分析

表5 底层节点X5与影响因素Yn关联性分析
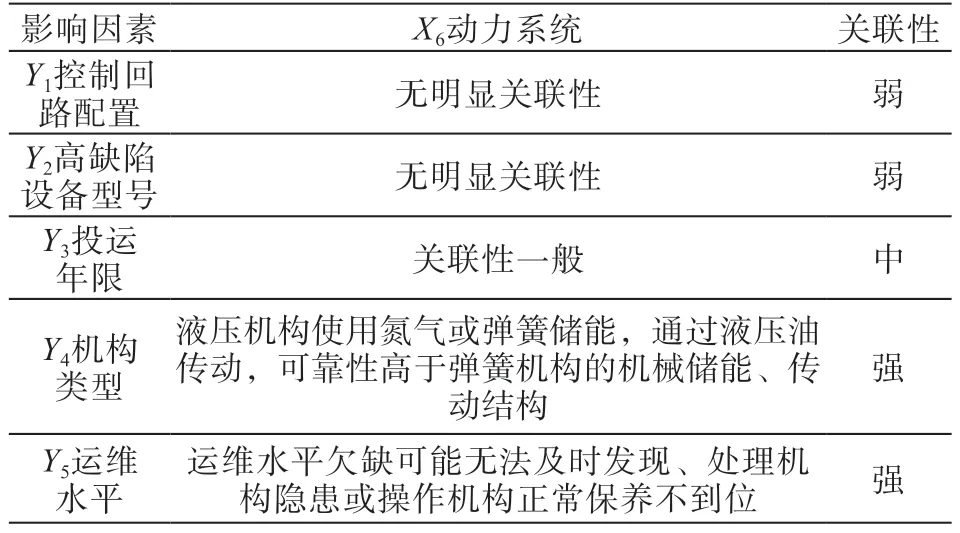
表6 底层节点X6与影响因素Yn关联性分析
通过以上论证得出底层节点Xi与影响因素Yn的关系,见图4。
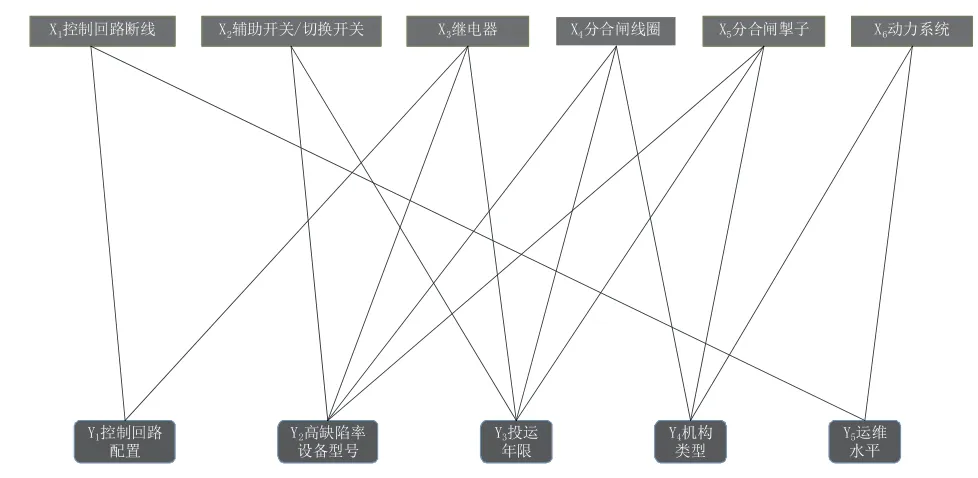
图4 底层节点Xi与影响因素Yn的关联关系
2.2.2 贝叶斯网络构建
基于以上故障树,建立的“影响因素—元器件—拒动”多层贝叶斯网络如图5,其中底层节点Xi均是通过“或门”(至少有一个叶节点发生时,根节点就发生)与上一层节点相连接。影响因素Yn是通过“与门”(多因素共同影响)与底层节点Xi相连接。

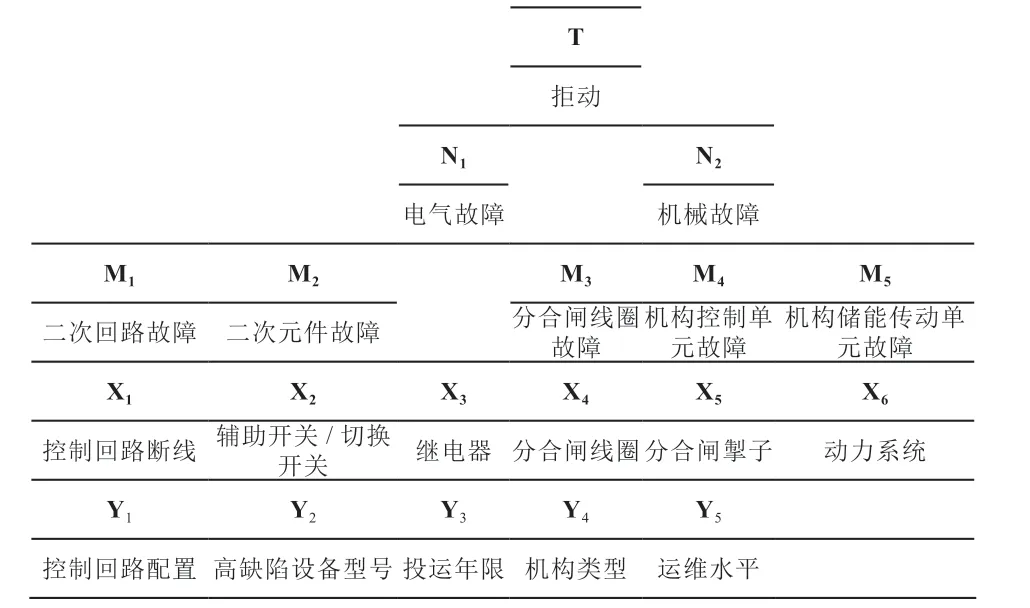
图5 高压断路器拒动的贝叶斯网络概率预测拓扑结构
根据高压断路器运行情况及拒动缺陷/事件情况,利用变电检修库专家经验,剔除偶发或不合理表述缺陷/事件,实现数据“清洗”,将每台高压断路器影响因素的定性特征(如型号:FXT11型)转化为定量特征(对应:Y2=2)。
Y1控制回路配置定级原则:500 kV高压断路器分闸回路均采用双重化配置;220 kV高压断路器的出线间隔的分闸回路采用双重化配置、母线间隔或变压器侧采用分闸回路单重化配置;110 kV高压断路器分闸回路采用单重化配置。具体如表7所示。

表7 Y1(控制回路配置)定级
Y2高缺陷设备型号定级原则:根据每个制造厂、每种型号的缺陷数、缺陷率确定。具体如表8所示。

表8 Y2(高缺陷设备型号)定级
Y3高缺陷设备型号定级原则:根据拒动缺陷发生率(某投运年限的缺陷数/某投运年限的设备总数*100%)与投运年限关系,以全网高压断路器拒动平均缺陷率为基准线,分为两个档次。具体如表9所示。

表9 Y3(运行年限)定级
Y4操动机构类型定级原则:通过统计近10年在运操动机构类型的缺陷数量,确定其缺陷率。具体如表10所示。
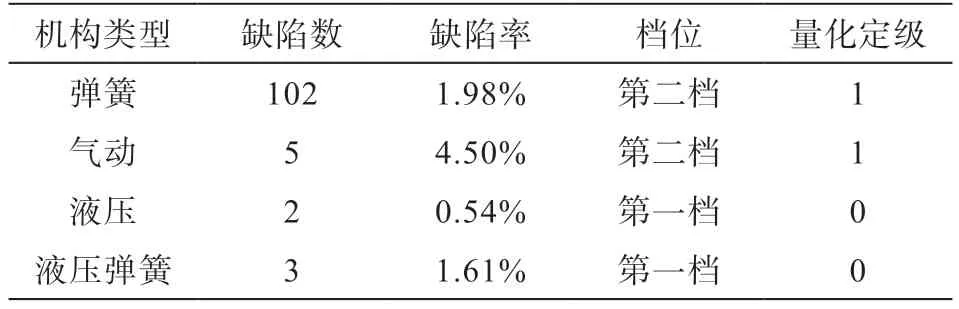
表10 Y4(操动机构类型)定级
Y5运维水平定级原则:依据专家评价(30位专家打分,熵权法计算处理)、变电设备缺陷情况(设备缺陷率占比50%、紧急重大缺陷占比50%)和运维人员情况(人员素质当量占比70%、缺员情况占比30%)三部分数据,以专家评价占比50%、变电设备缺陷情况占比30%、运维人员情况占比20%进行综合评估。具体如表11所示。

表11 Y5(运维水平)定级
2.3 贝叶斯概率预测
根据近10年的110 kV及以上电压等级高压断路器元器件缺陷情况,统计获得底层节点Xi的先验概率,如表12所示。
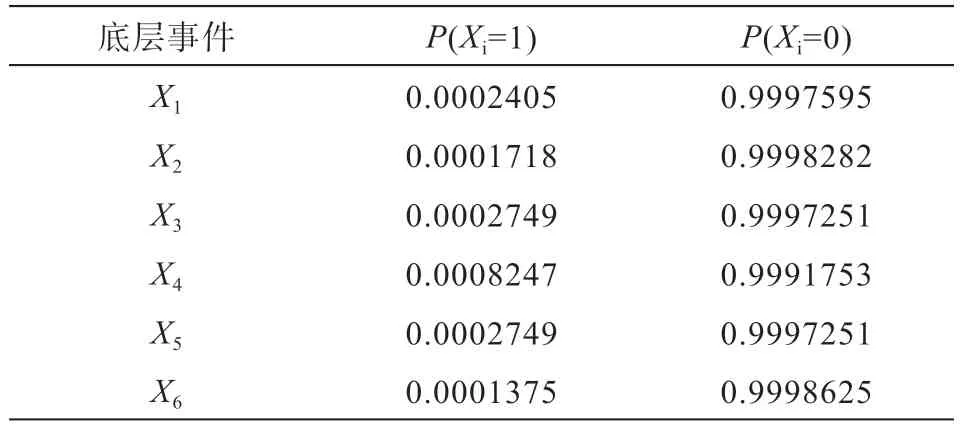
表12 各个底层节点的先验概率分布情况
根据近10年的拒动缺陷情况,建立影响因素Yn与底层节点Xi(定级:发生缺陷的赋值1,未发生缺陷的赋值0)之间的似然矩阵,得到似然系数,进一步修正Xi的概率,计算出Xi后验概率。具体公式如下:
构建贝叶斯网络预测模型,通过似然矩阵,得到某一台断路器Xi的后验概率,如表13所示。

表13 各个底层事件的后验概率分布情况
综合每个底层节点Xi修正的后验概率,根据以下公式,最终得到该台高压断路器可能发生拒动的概率P(T=1)。
将110 kV及以上电压等级的5820台高压断路器的影响因素进行计算,可得到69种影响因素组合下的预测概率。
3 模型验证
将以上69种场景进行排序,拒动概率最的为第1级,概率最低的为第69级。
利用k均值聚类算法对预测结果概率值进行概率级别分类,以确定需要重点关注的高概率高压断路器范围。将5820台高压断路器拒动预测结果概率值进行k均值聚类法(3聚类)分析,即可完成高概率(P≥0.36274%)、中高概率(0.19772%≤P<0.36274%)、中低概率(P<0.19772%)分类;按照该概率区间分类,得到高拒动概率高压断路器1067台,再次对1067台高压断路器概率进行k均值聚类法(2聚类)细化分析,即可完成超高概率(0.39883%≤P)、高概率(0.36274%≤P<0.39883%)分类。分析结果如图6和表15所示。

表15 概率区间定义
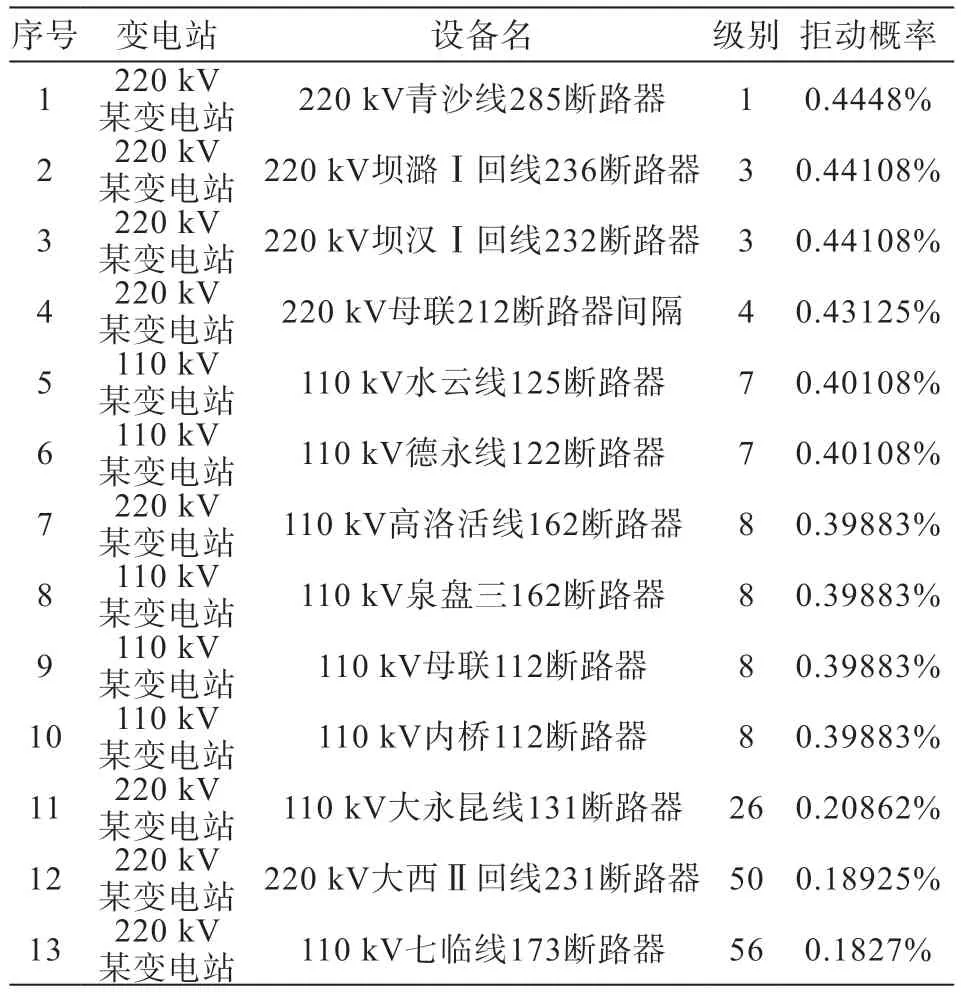
表16 某年拒动缺陷/事件模型验证情况
5020台高压断路器预测概率分布如图7所示。

图7 概率区间分布图
因此,基于概率值分布情况,认定超高概率区间高压断路器需重点关注(共679台,前8级)。
例如某年共发生13起拒动缺陷/事件,其中10起缺陷/事件可在超高概率区间(前8级)进行准确预测。
因此,通过以上建立的高压断路器贝叶斯拒动概率预测模型是可信的、有效的。
4 结束语
1)计算实验结果验证该方法对高压断路器拒动概率预测的有效性,可以利用较完备的运行数据和缺陷数据,缩小高压断路器防拒动预控范围,提升防控效率。
2)该方法是数据驱动的,使用过程中不依赖主观经验,具有良好的客观性和科学性。
3)该方法可以推广至变压器、电抗器、互感器、隔离开关、开关柜等变电站主设备的故障概率预测及诊断,提高设备状态掌控力。
