Quantitative characterization of cell physiological state based on dynamical cell mechanics for drug efficacy indication
2023-05-29ShuangMaJunfengWuZhihuaLiuRongHeYuechaoWangLianqingLiuTianluWangWenxueWang
Shuang Ma , Junfeng Wu , Zhihua Liu , Rong He , Yuechao Wang ,Lianqing Liu , Tianlu Wang , Wenxue Wang ,*
a State Key Laboratory of Robotics, Shenyang Institute of Automation, Chinese Academy of Sciences, Shenyang 110016, China
b Institutes for Robotics and Intelligent Manufacturing, Chinese Academy of Sciences, Shenyang 110169, China
c University of Chinese Academy of Sciences, Beijing 100049, China
d Department of Thoracic Surgery, Cancer Hospital of China Medical University, Liaoning Cancer Hospital and Institute, Shenyang 110042, China
e Department of Radiotherapy, Cancer Hospital of China Medical University, Liaoning Cancer Hospital and Institute, Shenyang 110042, China
Keywords:
Cellular mechanical properties
Cytoskeleton
Drug efficacy evaluation
Cell system modelling
Linear regression
ABSTRACT Cell mechanics is essential to cell development and function, and its dynamics evolution reflects the physiological state of cells.Here, we investigate the dynamical mechanical properties of single cells under various drug conditions, and present two mathematical approaches to quantitatively characterizing the cell physiological state.It is demonstrated that the cellular mechanical properties upon the drug action increase over time and tend to saturate,and can be mathematically characterized by a linear timeinvariant dynamical model.It is shown that the transition matrices of dynamical cell systems significantly improve the classification accuracies of the cells under different drug actions.Furthermore, it is revealed that there exists a positive linear correlation between the cytoskeleton density and the cellular mechanical properties, and the physiological state of a cell in terms of its cytoskeleton density can be predicted from its mechanical properties by a linear regression model.This study builds a relationship between the cellular mechanical properties and the cellular physiological state, adding information for evaluating drug efficacy.
1.Introduction
Cancer is one of the main killer diseases of human beings,causing high mortality, and remains a serious threat to human health [1].Despite the tremendous advances in cancer research,chemotherapy is still a mainstay of cancer treatment,and has become indispensable in the current medical management of malignant tumors[2].Clinically,anticancer drug resistance and heterogeneityamong the patient population are of the most severe problems of current cancer chemotherapy [3].For instance, although paclitaxel (PTX) is one of the most commonly used first-line chemotherapeutic drugs for treating a variety of tumors[4],its clinical efficacy in the treatment of breast cancer is dramatically affected by its drug resistance and severe side effects[5].The underlying reason is that,in the preclinical trials of a drug development, the two-dimensions (2D) and threedimensions (3D) cell models of in vitro cell experiments and the animal models of in vivo animal experiments are significantly distinctive from human models [6,7] and, furthermore, these preclinical trials ignore the heterogeneity among individual patients[8].In the clinical practice,anticancer drug susceptibility testing is often conducted before chemotherapy treatment, which can provide a reference for clinicians to make personalized medication decisions and seek precision medicine for individual patients so as to improve the clinical outcomes of chemotherapy[9,10].Despite the advance in sequencing and“integrated multi-omics”analysis technologies,due to the tumor heterogeneity and the limited number of known targets,it is still difficult to predict the response of a particular patient to an anticancer drug based on the data from molecular experiments[11,12].The ex vivo tests performed on primary patient-derived tumor samples,such as xenograft models[13]and tumor tissue slices[14], are limited by their drawbacks including time-consuming sample preparation,low throughput,and low success rate of establishing a xenograft model [15].The traditional in vitro drug susceptibility testing method on 2D or 3D culture models at cell population level suffers from insufficient number of cells[16],lengthy procedures[8]and high false positive rates due to the involvement of extra toxic reagents[8],and fails to detect heterogeneities in the cell population [8].Therefore, it is essential to develop an in vitro anticancer drug susceptibility testing method that can accurately evaluate the susceptibility of individual patients to anticancer drugs with less toxic or non-toxic compounds and short testing procedure,and reflect the tumor heterogeneity on single-cell level.
Cell mechanics is of great significance in cell development and function, and plays an essential role in human physiological activities and diseases [17].Cellular mechanics is closely related to cellular state, function and life activities, and the mechanical properties of cancerous cells affect cell motility[18],adhesion[19],metastasis[20],and epithelial-mesenchymal transition[21],and so on.Some studies have revealed that there exist significant differences in cellular Young's modulus and viscoelastic properties between normal cells and their cancer counterparts, such as lung cancer[21],stomach cancer[22],and lymphoma[23],the intrinsic softness is an inherent marker of highly tumorigenic and metastasis tumor cells [24], and the decreased membrane tension of cancer cells directly leads to a decrease in their stiffness which is strongly correlated with their increased invasion and metastasis efficiency [25].It has also been reported that drug action on cells often causes their structural changes and thus alters their mechanical properties[26].For example,the chemotherapeutic drugs,PTX and Cisplatin, can remodel the cytoskeletons of various cancerous cells, such as lung cancer [27], ovarian cancer [28], and breast cancer [29], and result in changes in their mechanical properties, and, on the contrary, the drugs, cytochalasin D and Latrunculin, can prevent the actins of hematopoietic cells from remodeling and decrease their elastic and viscous moduli [30].Furthermore, cell mechanics information upon drug action can be used to characterize therapeutic effects.For instance, the quantitative measurement of the binding affinity with the antibody drug,rituximab (Rtx), and the visualization of nanoscale distribution of the target antigens on the cells,both CD20s on lymphoma cancer B cells and FcRs on natural killer cells, indicate that the antigenantibody binding forces and the organization of the target molecules on the cells have significant impact on the therapeutic effect of B-cell non-Hodgkin's lymphoma [23,31,32], and the cellular surface roughness and cellular mechanical properties can be used to quantify the synergistic interactions between targeted drugs and chemotherapy drugs and to predict the efficacy of combinatorial drugs, cisplatin, cytarabine, and Rtx [30].Therefore, the study on cellular mechanics of cancers can advance our understanding of pathological processes of diseases and allow for evaluating drug efficacies in cancer treatments at the single-cell scale.
The rapid development of detecting technologies, such as optical tweezers[33],magnetic tweezers[34],atomic force microscopy(AFM)[35],and acoustic force spectroscopy(AFS)[36],enables the detection of cellular mechanical properties at the single-cell scale.Among these tools,AFM provides a unique advantageous capability of measuring versatile cellular mechanical properties with nanoscale spatial resolution and millisecond temporal resolution [35],and thus have attracted considerable attention from worldwide researchers to develop AFM-based methods to acquire cell mechanical properties, including morphological information [37],Young's modulus with Hertz-Sneddon model [25], multidimensional viscoelasticity properties with Kelvin model [38],standard linear solid model [38] and generalized Maxwell model[39],and so on,and to detect cell to cell adhesion[40]and molecule to molecule binding force on cells [31], etc.Furthermore, the power-low rheological behavior of cells has been of great interest in understanding cellular mechanical responses to external stimuli,and various models have been used to explain the power-law characteristics of cells [41-44].In particular, a self-similar hierarchical model has been proposed to spontaneously capture the power-law characteristics of creep compliance over time and complex modulus over frequency, and the dependence of the power-law exponent on cell stiffness and the frequency-dependent transition in power-law rheological behavior of living cells have been unraveled with this model [45,46], indicating potential mechanics-based biomarkers for cell classification and cancer diagnosis.However, most studies on mechanical properties of living cells and their relationship with cellular physiological states under the drug action were conducted at a single time point and ignore the dynamic evolutions in the physiological states and mechanical properties of cells.In fact,cells become stiff to keep acting as building blocks to maintain the mechanical integrity of living organisms and they do change their mechanical properties, if it is necessary, to behave more like fluids in order to differentiate,invade,and migrate[22].On the other hand,structural alteration in a cell due to drug stimulation proceeds gradually and thus its cellular mechanical properties involve a dynamic evolution over time.Therefore, it is of great interest in measuring dynamic evolution of cell mechanical properties at biologically relevant time scales(several hours),which will provide a better understanding of structural and functional changes that cells undergo and improve prediction of drug efficacies of cancer treatments.
In this paper, we firstly present a method to characterize the dynamic evolution of cell mechanics over time and then investigate the correlation between the dynamic cell mechanics and the cytoskeleton characteristics under drug action, which can be used to evaluate the cellular physiological state for drug efficacy indication at the single-cell scale.As shown in Fig.1,single cells are regarded as a linear time-invariant dynamical system,the output of which is the temporal mechanical properties of cells and the input is virtually a step function representing the mechanical stimulation by AFM indentation [47].The temporal mechanical property curves consist of the mechanical properties of the cells at selected time points at biologically relevant time scales, which are acquired by AFM indentation experiments.The dynamical cell system can be depicted by a state-space model [48], in which the state variables represent the black-box physiological state of cells and the system matrix A governs the cell state transition.It is worth noting that the cell system and its system matrix are assumed to be time-invariant for the simplicity of study, and they undergo a change under drug actions.Therefore, it may provide an approach to quantitatively distinguishing cellular physiological state by statistically analyzing the difference in the system matrice of cancerous cells before and after drug action,which may be used for drug efficacy evaluation.On the other hand,the mechanical properties of a cell are directly related to its cytoskeleton structures, and therefore the dynamic evolution of cellular mechanical properties under drug action is mainly caused by the alteration of cytoskeleton characteristics due to the drug action.If the correlation between the cell mechanics and the cytoskeleton characteristics can be mathematically described, then the cytoskeleton characteristics of a cell can be predicted with its mechanical properties, which may provide another approach to quantitatively evaluating drug efficacy by predicting the cellular physiological state in terms of cytoskeleton characteristics with the dynamics of cellular mechanical properties upon drug action.

Fig.1 .Schematic diagram of drug efficacy characterization based on the dynamical mechanical properties of single cells.A single cell is regarded as a system,and its input is a virtual input of step function and its output is its temporal mechanical properties The single-cell system is then depicted by a linear state-space model.The system matrix A governs the state transition of the cell system under a certain condition of drug action.According to the spatial distribution of eigenvalues of matrice A before and after adding dosing, the drug effect can be evaluated.
2.Experimental
2.1.Cell culture and sample preparation
The cell lines,human breast cancer cell line(MCF-7)and human embryonic kidney cell line (HEK293), used in this study were provided by Shenyang Pharmaceutical University.They were firstly cultured in complete RPMI-1640 medium (RPMI-1640 medium(Hyclone, Logan, UT, USA) + 10% (V/V) foetal bovine serum (FBS;Gibco, Carlsbad, CA, USA) + 1% (V/V) penicillin-streptomycin solution (HyClone) in a 5% CO2atmosphere in a humidified incubator(Thermo Fisher Scientific Inc., Waltham, MA, USA) at 37°C, and then were inoculated in a culture flask.When the cell density reached 80% confluence,they were passed onto Petri dishes with a diameter of 60 mm, which were then placed in the humidified incubator for 2-3 days before the experiments.The drugs, paclitaxel (PTX, item number SC0213; Beyotime, Shanghai, China) and doxorubicin (DOX, item number SC0159; Beyotime) were diluted with dimethyl sulfoxide (DMSO, item number ST1276; Beyotime),and phosphate buffer saline (PBS; Invitrogen, Carlsbad, CA, USA),respectively,to form the stock solution of 1 mM,which were stored in a -20°C refrigerator.In the experiments, the stock solution of PTX and DOX were taken out and melted in a 37°C water bath and then diluted with RPMI-1640 medium to get PTX solutions of 100 nM and 1000 nM and DOX solution of 100 nM,respectively.The original culture medium was extracted from the cell Petri dishes,and the complete RPMI-1640 medium, PTX solution and DOX solution were added into the Petri dishes, respectively, to perform AFM experiments to measure the mechanical properties of cells.The AFM experiments were performed with different batches of cells.All AFM experiments were performed in a liquid environment at room temperature of around 25°C.
2.2.Acquisition of force curves with AFM indentation
All AFM experiments were carried out with a Bioscope Catalyst AFM (Bruker, Billerica, MA, USA) (Fig.S1A) mounted on an inverted optical microscope (Ti, Nikon, Tokyo, Japan).The silicon nitride probe (MLCT, Bruker) was used, and the nominal spring constant of the cantilever was 0.01 N/m.To measure the mechanical properties of a living cell, an indentation experiment was performed with the AFM in the culture medium at contact mode.Before indenting the cells, force curves were obtained on the blank area of the substrate so as to calibrate the deflection sensitivity of the cantilever beam and its exact spring constant by the thermal noise module.The AFM tip was then positioned to the central area of the cell and controlled to indent the cell to obtain the mechanical properties of cells.The entire process of measurement takes an approach-stay-retract mode consisting of three phases, approach, stress-relaxation, and retraction [39,47],as shown in Fig.S1B.During the phases of approach and retraction, the piezoelectric (PZT) moved at a loading rate of 4 μm/s.The stress-relaxation phase started when the cantilever beam reaches the preset maximum deflection of 1 μm, and the PZT was kept at a constant depth and the tip was stayed on the cell surface for 6 s during the stress-relaxation phase.Afterwards,the probe was retracted for next indentation and the retract time was set to 3 s.During the measurement process, the forcedisplacement curves with respect to the PZT displacement were recorded by Nanoscope software (Bruker) and the temporal curves of force and PZT displacement were recorded by an oscilloscope (LeCroy, Chestnut Ridge, NY, USA) which was linked to the AFM (Fig.S1A).The Young's moduli of the cell were extracted according to Sneddon-modified Hertz model from the force-displacement curve in the approach phase (Fig.S2) to characterize the cellular elastic properties, and the multiple viscoelastic parameters were extracted according to the general Maxwell model from the temporal force curve in the stressrelaxation phase (Fig.S3) to characterize the cellular viscoelastic properties, respectively.
For a cell,a total of 10 indentation experiments were performed at different locations in its central area at a time point.The Young's moduli and the viscoelastic parameters were extracted from the force curves and the average values were taken as the mechanical properties of the cell at this time point.This strategy has been widely used for the measurement of cellular mechanical properties by AFM indentation [49,50], and can significantly reduce the influence of cell morphology on the measurement of cellular mechanical properties by AFM indentation.The time points for measurement were selected with a fixed time interval of 0.5 h within the time span of 4 or 8 h.In this experiment, a cantilever beam was used to detect all the cells so as to ensure that the relevant parameters (loading speed, residence time, and pressure displacement) were consistent.
2.3.Extraction of cellular mechanical properties
In this study, two types of cellular mechanical properties,Young's modulus and multiple viscoelastic parameters, were extracted respectively from the force curves at the selected time points.The dynamical mechanical property curves of cells are composed of the Young's moduli or the multiple viscoelastic parameters at all time points.
Young's moduli of the living cells were extracted by fitting the force curves with Sneddon-modified Hertz model [25]:
where F is the loading force exerted by AFM probe,E is the Young's modulus of a cell,δ is the indentation depth,θ is the half-opening angle of the conical tip, and ν is the Poisson ratio of the cell.Here ν = 0.5 with the assumption that the cells are nearly incompressible.The loading force F can be written as follows according to Hooke's law:
where k is the spring constant of the cantilever beam, and x is the deflection of the cantilever,which can be obtained directly from the force curves.
The multiple viscoelastic parameters of the cells were extracted based on the stress-relaxation force using the general Maxwell model [39,41]:
where u and y are the system input and output, respectively, the state variable xirepresents the relative displacement between the spring and the damper in the ith path and is closely related to cell formation, and kiand biare the elastic and viscous parameters of the corresponding springs and dampers, respectively.Here the input signal u(t) is the constant PZT z-position during the stressrelaxation phase of indentation process and the output signal y(t)is the stress-relaxation force curve.Studies suggest that the order of the system n = 2 based on system identification using the Hankel matrix method [39].The least squares method is then used to identify five viscoelastic parameters k0, k1, k2, b1, b2.
2.4.Single cell system modelling and identification
We have proposed a modelling method to characterize the dynamics of a living cell at biologically relevant time scales [41].In brief, a single cell is regarded as a linear time-invariant dynamical system,which can be written in the form of state space equations as follows:
where A, B, C, D, and K are parametric matrices, x(t) is the state of the system,u(t)is the virtual input of the system,y(t)is the output of the system, and e(t) is the noise of the system.Here the input takes a step function representing the mechanical stimulation by AFM indentation, and the output takes the temporal cellular mechanical property curves of either Young's moduli or viscoelastic parameters.In this model,the system matrix A determines the state transition of a cell system and has a significant effect on the temporal evolution of cellular mechanical properties,and therefore the matrix A can represent the cell system and characterize its physiological state.Hence, reasonably, the dynamical model is used to evaluate the drug efficacy on cancerous cells by measuring the statistical difference between the system matrices of the cells without drug action and those with drug action.In this study, the system matrices of the cells were identified,and their eigenvalues were used to measure the difference in cell system the system difference of the cells and to evaluate the drug efficacy.
2.5.3D confocal imaging of cytoskeleton and nuclei
3D confocal images of cytoskeleton and nuclei of the cells were obtained by a Confocal Laser Scanning Microscopy(Leica D-35578,Leica,Wetzlar,Germany).The Solarbio's TRITC Phalloidin dye(item number CA1610; Beijing, China) and the Solarbio's DAPI (item number C0065) solution (10 μg/mL ready-to-use) were used to stain the actin microfilaments (F-actin) of cytoskeleton structure and the nucleus of cells,respectively,according to the instructions after the cell slides were grown for 24 h and the density reached 50% confluence.The cell slides were mounted with water-soluble Fluoromount-G mounting tablets (SouthernBiotech, Birmingham,AL, USA) and permanently mounted with nail polish.3D confocal imaging of cells was implemented in order to observe the microfilament F-actin and nuclei of the cells with 561-nm laser and 405-nm laser, respectively.The volume of a cell and its integrated fluorescence intensity of F-actin cytoskeleton were calculated using ImageJ software, and then the average F-actin fluorescence intensity was calculated by dividing the integrated fluorescence intensity of F-actin cytoskeleton with the cell volume.
2.6.Statistical analysis
All statistical analyses in this study were performed using SPSS 20.0 software (IBM Corp, Armonk, NY, USA).Data are listed as the mean±standard deviations(SD).One-way ANOVA with Bonferroni method was used to determine the statistical differences in cellular mechanical properties among the control and experimental groups.P <0.05 for a two-tailed test.
3.Results and discussion
3.1.Effect of drug dosage on dynamical mechanical properties of cells
Drug dosage is an important factor to treat cancers and thus it is of great significance to characterize the drug effect on cells with respect to drug dosage.In this study, the temporal cellular mechanical property curves of MCF-7 and HEK293 cells were extracted upon the drug PTX action with different dosages.For each type of cells, the experiments are conducted with a control group without drug action and two experimental groups of low dose PTX (100 nM) and high dose PTX (1000 nM), respectively,and forty cells with similar morphology are selected in each group.For a cell,10 sets of force curves are recorded in every half an hour during 0-4 h, and 10 sets of Young's moduli and viscoelastic parameters are calculated at the corresponding time point and then averaged as the Young's modulus and the viscoelasticity parameters of the cell (n = 10).The typical temporal mechanical property curves of a single cell are shown in Fig.2 with respect to the control group and the experimental groups respectively, in which k0, k1, k2, b1, b2are the components of the viscoelasticity properties of cells.Furthermore, the statistically average mechanical properties of the cell populations with respect to the control group (n = 40 cells for the control group) and the experimental groups (n = 40 cells for each experimental group) and their significant difference analysis are shown in Fig.3.It is indicated from Figs.2 and 3 that the drug action of PTX enhances the viscoelasticity properties and Young's moduli of both types of cells and the cell structures become stiffer and more viscous.For the control group, the temporal cellular mechanical properties fluctuate in a small range,and there is no an obvious upward trend overtime.And, for the experimental groups, the mechanical property curves display an upward trend over time after dosing,which implies that the drug PTX takes effect.Especially, the cellular mechanical properties of the cells in the experimental group with high dosage reach a saturation level quickly in about 1 h and are much higher than those of the cells in the experimental group with lower dosage, indicating that the high dose PTX may have achieved its therapeutic effect to kill the cells.In contrast,the cells in the case of low dose keep the increasing trend in their cellular mechanical properties within the whole time span of the experiment, indicating that the low dose PTX has not achieved its therapeutic effect and may need longer time to do so.

Fig.2 .Temporal mechanical property curves of single cells during 0-4 h from the control group and two PTX groups.(A)MCF-7 cells and(B)HEK293 cells.Mechanical parameters of cellular viscoelasticity: k0, k1, k2, b1, b2, and cellular Young's modulus, respectively.PTX: paclitaxel.
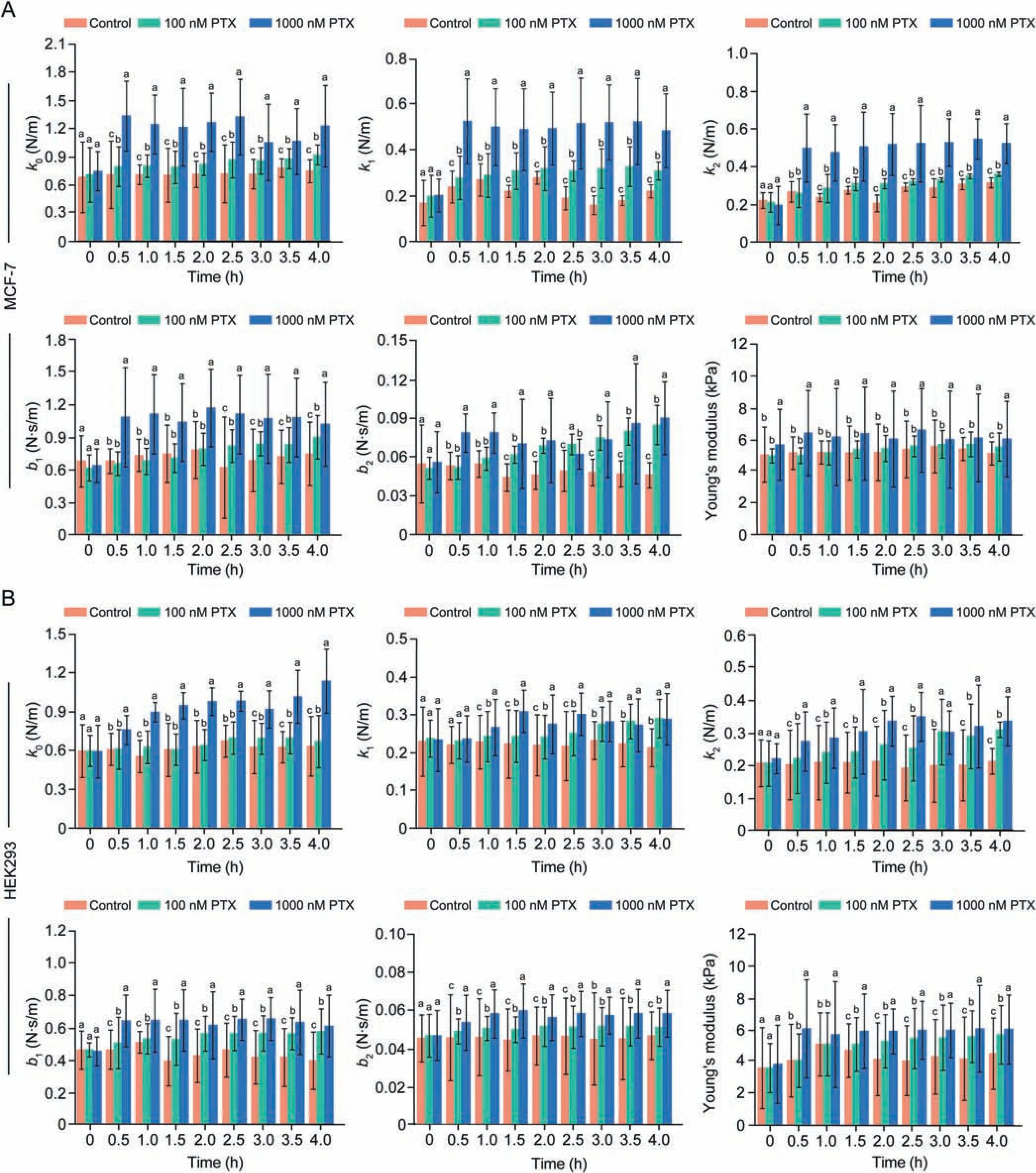
Fig.3 .Significant difference analysis of average cellular mechanical properties between the control group and two PTX groups.(A) MCF-7 cells and (B) HEK293 cells.Mechanical parameters of cellular viscoelasticity:k0,k1,k2,b1,b2,and cellular Young's modulus,respectively.The letters a,b,and c indicate significant differences among the groups(P <0.05).PTX: paclitaxel.
Furthermore, as shown in Fig.3, the analysis of variance(ANOVA)with the Bonferroni method indicates that the temporal mechanical properties of the cell populations upon the drug action of high dose PTX are significantly different from those of the cell populations in the control group and the experimental group with low dose PTX.However, some mechanical property parameters, such as b1and Young's modulus of the MCF-7 cell population and k1of the HEK293 cell population, in the experimental groups with low dosage cannot be well discriminated from those of the cell populations in the control groups,which further confirms that the low dose PTX of 100 nM may not achieve its therapeutic effect.
3.2.Effect of drug action time on dynamical mechanical properties of cells
As indicated above, the high dose drug can quickly take effect and may achieve its therapeutic efficacy in about 1 h while the low dose drug may take longer time to achieve its therapeutic effect.Therefore,drug action time is another significant factor,especially when the drug dosage is low, in clinical cancer chemotherapy.In this section, in order to characterize the drug effect on cells with respect to drug action time, the experiments are conducted with low dose PTX (100 nM) and DOX (100 nM) respectively and the time span is extended to 8 h.Similar to Section 3.1, the dynamic mechanical property curves of MCF-7 and HEK 293 cells were extracted for the control groups and the experimental groups respectively.The typical temporal mechanical property curves of single cells from the control group and the experimental groups are shown in Fig.4 (n = 10), and it is obvious that both PTX and DOX take effect and enhance the viscoelasticity properties and Young's moduli of the cells resulting in stiffer and more viscous cell structures.In the control group,the mechanical properties of the cells in the control group fluctuate without increasing tendency in a small range.However,upon the action of PTX and DOX with the low dosage of 100 nM, the mechanical properties of the cells evolve continuously over time and keep their increasing trend within the whole time span of 8 h, and some of the mechanical property parameters exhibit a saturation tendency indicating that the drugs will achieve their therapeutic efficacy soon.We divide the time span evenly to two phases,and compare the cellular mechanical property curves in these two phases.It is obvious that the cellular mechanical property curves in the experimental groups are well distinct from those in the control group in the latter phase (shaded area in Fig.4), and the differences are much more significant than those in the former phase(non-shaded area in Fig.4).

Fig.4 .Temporal mechanical property curves of single cells during 0-8 h from the control group, PTX group, and DOX group.(A) MCF-7 cells and (B) HEK293 cells.Mechanical parameters of cellular viscoelasticity: k0, k1, k2, b1, b2, and cellular Young's modulus, respectively.PTX: paclitaxel; DOX: doxorubicin.
The statistical average cellular mechanical properties of the cell population over the time are compared using significant difference analysis(n=680 for the control group(40 cells and 17 time points of measurement), n = 360 for the former phase of the PTX group(40 cells and 9 time points),n=320 for the latter phase of the PTX group(40 cells and 8 time points),n=360 for the former phase of the PTX group(40 cells and 9 time points),and n=320 for the latter phase of the DOX group(40 cells and 8 time points)).As shown in Fig.5,regardless of cell type and drug type,in comparison with the cells in the control group,the average mechanical properties of the cells in the experimental groups within the former phase and the latter phase are significantly increased due to the drug action,and the average mechanical properties within the latter phase are significantly higher than those within the former phase.And there do not exist the significant differences between the average mechanical properties in the former phase and those in the latter phase for the cells in the control groups, as shown in Fig.S4.Another interesting observation is that the difference between the mechanical properties of the cells upon the drug action of DOX and those upon the drug PTX are not significant in the former phase but become remarkable in the latter phase (Fig.4), and the cellular mechanical properties under the drug DOX are higher than those under the drug PTX at last,indicating that the same amount of DOX may make the cells stiffer than PTX.

Fig.5 .Significant difference analysis of the average cellular mechanical properties between the control group during 0-8 h,PTX group and DOX group within the former phase and the latter phase.(A)MCF-7 cells and(B)HEK293 cells.Mechanical parameters of cellular viscoelasticity:k0,k1,k2,b1,b2,and cellular Young's modulus,respectively.The letters a,b,and c indicate significant differences among the groups (P <0.05).PTX: paclitaxel; DOX: doxorubicin.
3.3.Cell system modelling and spatial characterization of single cells
It has been shown in the previous sections that the mechanical properties of cells evolve over time under the drug action.We have reported that a cell can be regarded as a system and it can be modeled,within a time span of 4 h as a linear timeinvariant system, the output of which is the temporal cellular mechanical properties and the input is virtually a step function[41].The detail of modelling process has been briefly described in Section 2.In the dynamic model,the system matrix A governs the evolution of the mechanical properties of a cell and thus may represent the cell system.Upon the drug action,the physiological state of the cell changes and thus the system matrix varies causing different transition matrix A.If the drug action time is long enough, the cell system and its corresponding transition matrix will change over time too.In this study,it is assumed that the cell system is a constant system within 4 h.Thus, in the case of drug action time of 8 h, a cell is modeled for its former phase and latter phase respectively, meaning that the system matrix A of the cell changes from its former phase to its latter phase of drug action time.The drug effect with different dosages on the cell system was investigated by modelling the cells under PTX action of different dosages with their temporal viscoelastic parameters and Young's modulus, respectively.The system identification results show that the order of the single-cell system based on Young's modulus is two, while the system order based on the viscoelastic parameters is three.It is shown that both viscoelasticity properties and Young's moduli of a single cell can be well fitted with the identified dynamic models(Figs.6A and S5, and Figs.6B and S6).By comparing the curve fitting results, it is observed that the dynamic model of a cell based on the cellular viscoelasticity properties can provide a better fitting than that based on the cellular Young's moduli,indicating that the dynamic model based on the multiple cellular viscoelasticity properties can better describe the cell system than that based on the cellular Young's moduli.In order to visualize the cell system with the transition matrix A, the eigenvalues of the matrix A of a cell are used to characterize the cell distribution in a system space according to the flow charts in Figs.S7 and S8 which correspond to the viscoelastic parameters and Young's moduli, respectively.Accordingly, the cells of MCF-7 and HEK293 from the control group and experimental groups are depicted using their eigenvalues of matrix A with respect to their cellular viscoelasticity (Figs.6A) and cellular Young's moduli (Figs.6B),respectively.Apparently, regardless of cell type, compared with the cells in the control group that are scattered in the space(orange dots), the cells in the two PTX groups are more clustered(green dots and blue dots), and the cells in the 1000 nM PTX group are the most clustered(blue dots).It is also shown that the distributions of the cells, especially with respect to the multiple viscoelasticity properties, from the three groups are centered at different locations in the space, which indicates that the cells from the three groups can be discriminated with their transition matrix of cell system.The cells from the three groups were classified with the cellular mechanical properties at the single time points (0-4 h), the temporal curves of cellular mechanical properties (curve), and the transition matrices of cell system(iden), respectively, using 6 different Support Vector Machine(SVM) algorithms in Classification Learner of Matlab.The 6 different SVM algorithms have different kernel functions, which are linear, quadratic, cubic, fine Gaussian, medium Gaussian, and rough Gaussian functions, respectively.The statistical classification accuracies of these 6 algorithms under different cases are shown in the boxplots in Figs.6C and D and Tables S1-S4.Obviously, regardless of cell type, the classification accuracies with the multiple viscoelasticity properties are always higher than those with the Young's moduli counterparts, which mean that the multiple cellular mechanical properties are a better biomarker than the cellular Young's modulus.Moreover, the classification results based on the temporal curves of cellular mechanical properties are better than those based on the mechanical properties at the single time points, and the reason is that the temporal curves of cellular mechanical properties can reflect the dynamic characteristics of the cells.Most importantly,the classification results can be further improved with the system transition matrices, indicating that the system modelling based on the temporal mechanical properties of cells provides an approach to quantitatively characterize the physiological state of cells and to evaluate the drug efficacy on cells.It is also observed that it is easier to discriminate the cells upon the drug action of high dose PTX from those in the control group and the experimental group with low dose PTX, which is consistent with the observation based on the temporal mechanical properties in Section 3.1 and confirms that the low dose PTX of 100 nM has not achieved its therapeutic effect yet within 4 h.
In addition, the drug effect with different drug action times on the cell system was investigated by modelling the cells under the low dose drugs with their temporal viscoelasticity properties within the former phase and the latter phase of action time,respectively.The Young's modulus curves of cells were not used to model the cell systems any more since they are not as good as the viscoelasticity curves of cells in terms of a biomarker of cells.As shown in Fig.7A, the cells are depicted using their eigenvalues of matrix A, representing the cells in the control group and those in the experimental group within the former phase and the latter phase of drug action,respectively.Obviously,regardless of cell type and drug type,compared with the cells in the control group that are dispersed in the space(orange dots),the cells corresponding to the former phase(blue dots)and to the latter phase(green dots)in the experimental groups are more clustered,and the cells with respect to the latter phase of drug action time are the most clustered.And the three populations of cells are centered at different locations in the space, indicating that their physiological states can be distinguished with their transition matrices of cell system.Here,we used 6 SVM algorithms to classify the cells in the control group and those in the experimental group with respect to the former phase and the latter phase of the drug action time, respectively, with their transition matrices of cell system (Fig.7B and Table S5).Regardless of cell type and drug type, the cells in the three populations can be well distinguished (yellow bars) with classification accuracy of above 80%, and, especially, the cells upon the drug action within 4-8 h can be better discriminated from those in the control group(green bars) with classification accuracy of above 90% and from those upon the drug action within 0-4 h with classification accuracy of above 85% (orange bars), respectively.However, classification accuracies of the cells upon the drug action within 0-4 h and those in the control group are only between 60% and 80% (blue bars).The classification results are consistent with the observation in Section 3.2 that the mechanical property curves of the cells in the experimental groups in the latter phase but not the former phase are significantly different from those of the cells in the control groups.Therefore, the system modelling based on the temporal mechanical properties of cells can be used to evaluate the drug efficacy on cells at different phases of drug action time and to characterize the corresponding cellular physiological states.
3.4.Cytoskeleton characterization with cellular mechanical properties
It is well known that mechanical properties of cells are directly related to cytoskeletal characteristics [45].It is of great interest to investigate the drug effect on the cytoskeleton and quantize the relationship between the cellular mechanical properties and the cytoskeletal characteristics upon the drug action.Therefore, 3D confocal imaging of cell nucleus and cytoskeleton F-actin was performed for the cells with respect to the control groups and the experimental groups at the 4 h and the 8 h,respectively,and twenty cells were selected in each case to acquire the confocal images of cell neuclei and F-actin components.As shown in Figs.8A and B,regardless of the cell type, the cytoskeleton F-actins of single cells are sparse in the control groups,and become much denser upon the drug action of PTX and DOX.As shown in Figs.8C and D and Tables S6 and S7, the statistical average cytoskeleton densities,represented by the average F-actin fluorescence intensity,of the cell populations were compared using significant difference analysis.It is indicated that the cytoskeleton density of cell population is significantly affected and increases monotonically with the drug dosage(Fig.8C)and the drug action time(Fig.8D),respectively.It is also observed that, regardless of the cell type, the cytoskeleton density of cell population under the drug DOX is higher than that under the drug PTX at the same action time (Figs.8D), which is consistent with the observation on the cellular mechanical properties.
Now a question arises as whether the mechanical properties of cells can be used to quantitatively estimate the cytoskeleton characteristics since both of them increase with the drug dosage and the drug action time.It is impossible to measure the cellular mechanical properties and the cytoskeleton density on the same cell, and therefore,in this study,the investigation of the relation between the cellular mechanical properties and the cytoskeleton characteristics is based on the statistical averaged data of the cell populations.Among the experiments that were conducted, for each cell type, the 3D confocal images of cytoskeleton F-actins were recorded on 20 cells as a cell population in each of the following 6 distinct groups: the control group without drug action,the experimental group with low dose PTX at 4 h,the experimental group with high dose PTX at 4 h,the experimental group with low dose PTX at 8 h,the experimental group with low dose DOX at 4 h, the experimental group with low dose DOX at 8 h.Correspondingly, there are 6 cell populations of 40 cells for extracting the cellular mechanical properties in these 6 groups.A pseudo dataset of(M,Sd)where M represents the cellular mechanical properties and Sdthe cytoskeleton density was created by randomly choosing 80% cells from a cytoskeleton-oriented cell population and 80% cells from the corresponding mechanical property-oriented cell population and then averaging their cytoskeleton density and cellular mechanical properties respectively which results in a pair of(M,Sd).The process was repeated 10 times for each pair of cell populations and a dataset consisting of 60 pairs of(M,Sd)was created for each cell type.
In order to investigate the relationship between the cytoskeleton density and the cellular mechanical properties,we firstly used the Pearson's correlation analysis to analyze the relationship between the cytoskeleton density and the single components of the multiple viscoelasticity properties and the Young's modulus,respectively.As shown in Fig.S9, the Pearson's correlation coefficients,r, between the cytoskeleton density and the single components of the viscoelasticity properties or Young's modulus,are all greater than 0.4 except for that with the third elastic parameter of the viscoelasticity properties of HEK 293 cells, indicating the existence of the moderate and strong positive correlations between the cytoskeleton density and the mechanical properties of cells.Therefore,it is reasonable to assume that the relationship between the cytoskeleton density and the mechanical properties of cells can be written by a linear regression model as below:
where M is either the vector of cellular viscoelasticity properties,i.e.M = (k0, k1, k2, b1, b2)T, or the cellular Young's modulus, Sdthe cytoskeleton density, and α and β the parameters that need to be solved.We examined the model for each cell type from the perspectives of drug dosage of PTX, drug action time of PTX, drug action time of DOX, and all cases, and the models were trained with the method of least squares.As indicated by the coefficient of determination,R2,in Fig.9A,the data,from all perspectives,can be well fitted by multiple linear regression models with respect to the cellular viscoelasticity properties.Especially,the good fitting result of the multiple linear regression model to the data of all cases indicates that the dependence of the cytoskeleton density on the multiple viscoelasticity properties has no bearing on what factors,such as drug type, drug dose or drug action time, cause their changes and therefore the cytoskeleton density of a cell may be predicted by a fixed multiple linear regression model with the viscoelasticity properties irrespective of drug action conditions.The data can also be fitted by simple linear regression models with respect to the cellular Young's modulus,while the fitting results are not as good as those with the cellular viscoelasticity properties.On the other hand,we used the models trained with the whole pseudo dataset to estimate the average cytoskeleton density of 20 cells in the skeleton-oriented cell populations with the average mechanical properties of 40 cells in the corresponding mechanical propertyoriented cell populations.As shown in Figs.9B and C, the average cytoskeleton densities (orange bars)of the cell populations can be well approximated by the linear regression models, and the estimation with the viscoelasticity properties (green bars) is much better than that with the cellular Young's moduli (blue bars).Therefore, compared with the cellular Young's modulus, the multiple viscoelasticity properties of a cell can better reflect its cytoskeleton characteristics and thus are a better biomarker.

Fig.9 .Correlation between the cytoskeleton density and the mechanical properties of cells.(A)Prediction of cytoskeleton densities of MCF-7 cells from their mechanical properties with the linear regression models.(B) Prediction of cytoskeleton densities of HEK293 cells from their mechanical properties with the linear regression models.(C) Fitting performance of the trained linear regression models in terms of mean square error (MSE) and R2.PTX: paclitaxel; DOX: doxorubicin.
Here, we have shown that the mechanical properties of cells dynamically evolve over time upon drug action and reflect the cellular physiological state.Upon the drug actions of PTX and DOX,the temporal mechanical properties of cells display an obvious upward trend,which indicate that the drugs take effect and make the cells stiffer.The drug dosage and the drug action time are two important factors to affect drug efficacies.In this study,the cellular mechanical properties increase with the drug dosage and the drug action time.The mechanical properties of cells increase quickly under the drug action of high dosage(1000 nM)and reach a saturation level in about 1 h,while it may take about or more than 8 h for the cellular mechanical properties to reach the saturation level under the drug action of low dosage(100 nM).The dynamic evolution of mechanical properties of a cell can be modeled bya linear time-invariant system in the form of state space equations within a short time period,for example 4 h,and thus the cell state can be represented the system transitionmatrix in avector space.The classification results of the cells under different drug conditions prove that the temporal curves of cellular mechanical properties make the classification accuracies higher than the cellular mechanical properties at single time points, and the system transition matrices can further improve the classification performance, implying that dynamics of the cellular mechanical properties and especially its representation with the linear time-invariant model can better characterize the drug efficacy on cells.Accompanied by the increase in themechanical properties of cells under the drug action, the cytoskeleton structure becomes much denser,which is consistent the mechanisms of drug action of PTX and DOX.As a cytoskeleton stabilizing reagent,PTX can maintain the stability of tubulin and inhibit cell mitosis by promoting polymerization and preventing depolymerization of cytoskeleton proteins [47], while DOX induces cytoskeletal actin remodeling and promotes cortical actin contraction which makes the cytoskeleton volume smaller and the cytoskeleton density higher[49].It is of great significance that, for a type of cells, the cytoskeleton density is positively correlated with the cellular mechanical properties regardless of drug action conditions, which can be described by a linear regression model,and thus the cytoskeleton density of a cell can be estimated by its mechanical properties.Since the cytoskeleton density of a cell is closely related to its physiological state, the mechanical propertyof cells can beused to characterize thecellular state with the linear regression model.It is also shown that the results of cell classification accuracy, goodness of fit and prediction of cytoskeleton density with the multiple viscoelasticity properties of cells are better than the cellular Young's modulus,which means that the multiple viscoelasticity properties are a better biomarker than the Young's modulus to characterize the cell state upon the drug action and to evaluate the drug efficacy on cells.The underlying reason is that single cells exhibit viscoelastic characteristics under the interaction of the nucleus and cytoskeleton.Thus,the cellular viscoelasticity can better reflect the flow characteristics of cytoplasm of a cell and is more closely related to the cellular physiological activity than the cellular Young's modulus.
4.Conclusion
In this study, we investigated the dynamical mechanical properties of cells with respect to drug dosage and drug action time,respectively,and presented two approaches to quantitatively characterizing the cellular physiological state for drug efficacy indication with the temporal mechanical properties, one of which is characterizing the cell systems with a linear time-invariant dynamical model and another predicting the cytoskeleton density with a linear regression model.In comparison with the cells in the control group, the cells upon the drug action of PTX and DOX become stiffer and more viscous and their cellular mechanical properties evolve dynamically and increase with the drug dosage and the drug action time, displaying a significant upward trend which will approach to a saturation level.From the point of view,the cells were treated as a system and they were characterized by a linear time-invariant model in the form of state space equations with their mechanical properties as the system outputs.And therefore the system transition matrices can represent the cells in a vector space and were used to distinguish the physiological states of cells upon different drug conditions with SVM.The comparison of classification results demonstrates that the temporal curves of mechanical properties offer better capability of differentiate cell states than the mechanical properties at a single time points and the system transition matrices can further improve the classification accuracy, indicating the dynamics of mechanical properties can better characterize physiological state of a cell.More importantly,upon the drug action,the cytoskeleton structure of a cell become much denser and there exist linear positive correlations between its cytoskeleton density and the single components of its multiple viscoelasticity properties and its Young's modulus.Therefore, the physiological state of a cell in terms of its cytoskeleton density can be predicted by a linear regression model from its multiple viscoelasticity properties or its Young's modulus.It is also worth noting that the multiple viscoelasticity properties are a better biomarker than the Young's modulus to characterize the cell's physiological state.The results show the potential of our proposed approaches for mathematically characterizing the physiological state of cells and quantitatively assessing the drug efficacy on cells with their dynamical mechanical properties at the single-cell scale.
CRediT author statement
Shuang Ma: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Writing - Original draft preparation;Junfeng Wu: Investigation, Data curation;Zhihua Liu: Methodology, Supervision;Rong He: Resources;Yuechao Wang:Supervision;Lianqing Liu:Writing-Reviewing and Editing,Funding acquisition;Tianlu Wang: Funding acquisition;Wenxue Wang: Conceptualization, Methodology, Writing - Reviewing and Editing, Funding acquisition.
Declaration of competing interest
The authors declare that there are no conflicts of interest.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant Nos: U1908215, 61925307, 62003338,and 61933008), CAS Project for Young Scientists in Basic Research(Grant No: YSBR-041), Liaoning Revitalization Talents Program(Grant No: XLYC2002014), Natural Science Foundation of Liaoning Province of China (Grant No: 2020-ZLLH-47), and Joint fund of Science & Technology Department of Liaoning Province and State Key Laboratory of Robotics, China (Grant No:2019-KF-01-01).
Appendix A.Supplementary data
Supplementary data to this article can be found online at https://doi.org/10.1016/j.jpha.2023.03.002.
杂志排行
Journal of Pharmaceutical Analysis的其它文章
- Recent progress in aptamer-based microfluidics for the detection of circulating tumor cells and extracellular vesicles
- Breath-by-breath measurement of exhaled ammonia by acetonemodifier positive photoionization ion mobility spectrometry via online dilution and purging sampling
- Solriamfetol impurities: Synthesis, characterization, and analytical method (UPLC-UV) validation
- Recent applications and chiral separation development based on stationary phases in open tubular capillary electrochromatography(2019-2022)
- A chiral metal-organic framework {(HQA)(ZnCl2)(2.5H2O)}n for the enantioseparation of chiral amino acids and drugs
- High-throughput transcriptional profiling of perturbations by Panax ginseng saponins and Panax notoginseng saponins using TCM-seq
