基于Proteus 的BLDCM 建模与滞环电流控制仿真
2023-05-29何凡锋马瑞娜吴忠得
何凡锋,马瑞娜,吴忠得
(首都航天机械有限公司,北京,100076)
0 引言
Proteus 软件是Labcenter Electronics 公司开发的EDA 工具软件,它具有强大的原理图设计、电路仿真、PCB设计功能,能实现完整的电子设计,在嵌入式开发领域应用十分广泛。但是,它与matlab 等高级仿真软件相比,在无刷直流电机仿真方面存在一定不足,其仿真模型的数量与模型仿真功能较少。软件自带的motors 库里面,只有BLDC-STAR、BLDC-TRIANGLE、MOTOR-BLDCM 三 种 无刷直流电机仿真模型。目前,学者只能利用这些模型进行简单的仿真试验研究。王家豪[1]等学者, 以80C51 为控制核心,利用BLDC-STAR 模型进行了仿真,只给出了Hall 传感器输出信号波形;孙晓旭[2]等学者,利用AVR 单片机并结合BLDC-STAR 模型,以额定速度200 r/min 进行开环与闭环控制仿真,仅得出196.4 r/min 与199.9 r/min 的两个结果;王伟[3]等学者,利用Arduino 单片机与BLDC-STAR模型进行了闭环控制仿真,只展了速度与电流简单波形;高珮文等[4]学者,设计了无刷直流电动机控制系统,并利用MOTOR-BLDCM 模型进行了仿真,只给出了H 桥的输出波形与霍尔速度检测脉冲波形。显然,这些研究表明,系统自带的仿真模型只能获得BLDCM 系统变量的简单数据,无法获取瞬时扭矩、电流、反电势、转子速度等全过程的精确仿真细节信息。
为了在仿真过程中提供更多的BLDCM 仿真细节,本文先利用Proteus 的ASIMMDLS 库、DSIMMDLS 库与LAPLACE 库的库元件,并结合系统函数,采用自制仿真元件的思路,构建一个新的BLDCM 原理图仿真模型。然后,用滞环电流控制方法验证仿真模型的正确性。最后,用Matlab 进行仿真比对分析。
1 数学模型
BLDCM 采用星形连接、三相六状态形式。根据参考文献[5~7],电压平衡方程整理如下:
式中,Ua、Ub、Uc是三相电子电压(V);R为三相定子绕组的相电阻(Ω);ia、ib、ic是三相电、子电流(A);Ls为自感与互感的等效电感(H);p是微分算子(d/dt);Ea、Eb、Ec是三相定子的反电动势(V)。其中,Ea=pnfluxωrφa(θe)、Eb=pnfluxωrφb(θe)、Ec=pnfluxωrφc(θe),函 数φa、φb、φc函 数各取值范围都是[-1~+1],pn是电机极对数,flux是单相绕组的磁链(Wb),θe为转子电角度(rad),ωr为转子机械角速度(rad/s)。
电磁转矩方程:
其中,Te为电磁转矩(N.m)。
为了便于计算,令KEa=pnfluxφa(θe)、KEb=pnfluxφb(θe)、KEc=pnfluxφc(θe),根据前面提到关系,约掉速度ωr,得到简化公式:
另外,从力学角度,转子的转矩计算为:
其中,B为阻尼系数(N.m.s/rad);J为电机转动惯量(kg.m2);TL为负载转矩(N.m)。
转子的角度与角速度关系为:
其中θr为转子的角度(rad),电角度θe关系为θe=pnθr。
2 仿真电路
电路采用了自制元件模型的方式构建,BLDCM 的仿真模型以及滞环电流控制系统[8]如图1 所示。主要模块包括U1(PI 闭环计算模块)、U2(反PARK 变化模块)、U3(滞环比较与逆变器模块)、U4(BLDCM 电机模块),都是自制元件。图中下方,K 模块是速度ωr的单位转换比值(30/π)乘积模块,用于将速度的单位转换,由(rad/s)转为(r/min)。图中文本部分,以*DEFINE 开头的内容是Proteus 的脚本语言,用于定义一些仿真时需引用的常量。
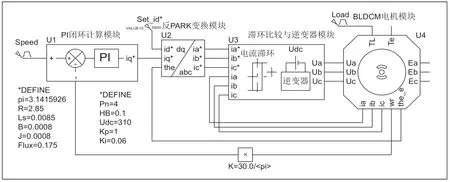
图1 电机滞环电流控制框图
电流滞环控制的基本原理:首先,通过检测各相的瞬态实际输出电流(ia、ib、ic),然后与给定的电流进行比较(ia*、ib*、ic*),当实际电流大于给定值,则通过改变逆变器的开关状态,让电流减少,反之增大。这样,可以控制实际电流绕给定电流做上下锯齿状变化,处于一定的变化范围,这是是一种Bang-Bang 控制方法。这个滞环电流控制系统包括两个闭环,转速控制环与电流滞环控制环。电流滞环控制环采用Bang-Bang 控制,不仅控制简单,而且不依赖于电机参数,鲁棒性好。以B 相为例说明控制过程,当反馈电流ib的瞬时值与给定电流ib*之差达到滞环的上限时(ib*-ib≥HB/2,HB 为滞环宽度),逆变器控制B 相上桥臂关闭,下桥臂导通,导通电压为-Udc/2,电流ib下降;反之,当反馈电流ib的瞬时值与给定电流ib*之差达到滞环的下限时(ib*-ib≤HB/2),逆变器控制B 相下桥臂关闭,上桥臂导通,导通电压为+Udc/2,电流ib上升。这样,通过桥臂开关的器件的交替通断,控制实际电流与给定电流一直处于滞环范围之内。
整套仿真系统的控制流程:首先,由PI 闭环计算模块将给定的目标速度Speed 与反馈速度进行差值计算,并按设定的Kp、Ki 值进行PI 计算得出目标iq*(采用了id*=0 控制策略)。然后,经过反PARK 变化模块得出目标控制电流ia*、ib*、ic*。接着,由滞环比较与逆变器模块对给点的电流值以及反馈的电流值进行比较,输出电机的三相电压控制信号Ua、Ub、Uc。最后,BLDCM 电机模块根据给定的电压信号以及负载Load 情况计算模拟电机运行,并输出ia、ib、ic、Ea、Eb、Ec、ωr(wr)、θe(the_e)等实时信号。
下面,介绍各个模块的内部原理图结构做介绍。
2.1 PI 闭环控制模块
该模块的内部原理图如图2 所示。+号是Speed 的输入端子,-号是反馈速度ωr的输入端子。iq*是PI 运算后的输出端子。这里利用ASIMMDLS 库的两种元件搭建PI 控制算法。

图2 PI 闭环控制模块图
ACS1(Arbitrary Voltage Controlled Current source) 与理想电容C1 构成一个积分器。ACS1 的电流大小就是左侧两引脚电压的差值err=V(A,B)=V(A)-V(B)。它再乘以-Ki 积分比值就表示:差值是正的时候,电流流向C1,表示充电,C1 两端电压升高;相反,差值是负的时候,C1 放电,两端电压降低。根据电容与电流的微分关系uc=1/C*∫icdt,当C=1F 时,电容的电压就是电流的积分值。因此,uC1=Ki*∫errdt。SUM1(Ideal 2 Input Adder)是理想的电压加法器,它的输出效果就是:Kp*err。SUM2 的输出结果就是:
2.2 反PARK 变换模块
反PARK 变换的目的是要将同步旋转坐标系下的id*、iq*转换为自由坐标系下的ia*、ib*、ic*,内部原理图如图3 所示。

图3 反PARK 变换模块图
MULT1(Ideal 4 Quadrant Multiplier)~MULT6 是 理 想的乘法运算器,也是ASIMMDLS 库的元件,它可以实现输入端V(A)与V(B)的乘法运算,也可以按需要做其它运算,如图中插入三角函数运算。the引脚是电角度θe的输入引角。图中描述的关系就是:
MULT2 与MULT1 串联就表示两者的乘法结果进行求和计算,属于电压叠加,这种串联方式可以节约SUM 元件的使用。
2.3 滞环比较与逆变器模块
这个模块是比较给定电流与实际电流瞬时差值的关键模块,内部原理图如图4 所示。实际电流瞬时值ia、ib、ic做了5e-6s 微小延时处理,这是为了保持与参考资料[8]一致,后续Matlab 仿真也设置了这样的延时。这个模块混合使用了ASIMMDLS 库与LAPLACE 库的元件。

图4 滞环比较与逆变器模块图
NL1(Laplace Non-linear Two-Level Switch With Hysteresis)~NL3 是非线性滞环比较器,它有四个内部参数,阈值下限、阈值上限、输出下边界、输出上边界,这里分别设置为-
2.4 BLDCM 电机模块
BLDCM 电机模块是由ASIMMDLS 库元件组成,内部原理图如图5 所示。模块分成(a)、(b)、(c)、(d)四个功能区块。区块(a)展示了电机三相绕组的连接形式,各相分别由一个反电势(AVS 可控电压源)、一个理想电感Ls、一个电阻R 串联而成,各相的末端分别汇集到一点,成星形连接。反电势AVS 的大小由其+极输入端电压控制,分别是Ea、Eb、Ec 端子。并联在电阻上端的AVS 可控电源用于检测相电流的瞬时大小,并输出与电流等值的电压信号,分别以ia、ib、ic 端子输出。
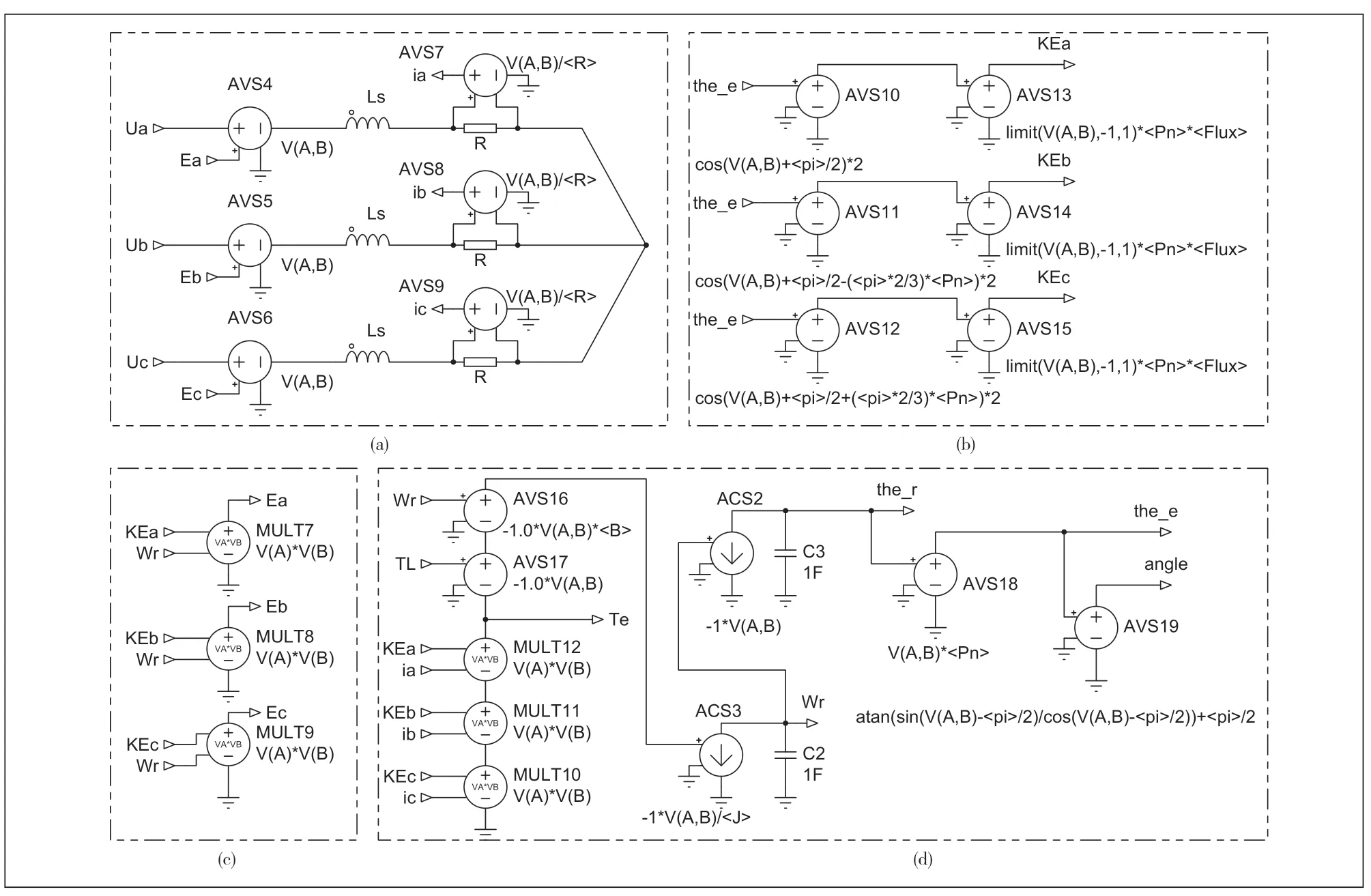
图5 BLDCM 电机模块图
区块(b)用于实现系数KEa、KEb、KEc的计算,用了6个AVS 压控电压源,分别调用了cos、limit 函数。反电势φa、φb、φc函数采用了cos 来模拟[9],宽度为120°,limit函数用于限制幅值处于[-1~+1]之间,分别乘以pnflux后得到KEa、KEb、KEc。区块(c)通过MULT 电压源分别计算Ea、Eb、Ec。区块(d)的功能是实现转子角速度与角度的计算,主要根据公式(3)~(5)来计算。按照公式(3),利用三个MULT 电压源串联,利用电压叠加得到电磁转矩Te。上端串入AVS17 模拟负载转矩TL,前面带-1.0 系数表示负电压,起到相减的效果,这里带了输入端子,可以从电机模块外部输入负载阶跃信号传递到这里。AVS17 上面,再串接AVS16 模拟阻尼系数B 产生的阻力,前面也带-1.0 系数表示负电压。它的输出端电压通过ACS2 与C1 的配合,形成积分效果,C1 的上端电压就是模拟转子速度ωr,再利用ACS1 与C2 积分,得到转子的角度θr,利用AVS18 乘以极对数pn得到电角度θe。下面的angle 角度是为了波形显示,将连续的θe角转换为0~2π 取值范围的转子角度。
3 仿真试验
仿真试验采用相同的电机参数,分别做两种仿真试验:Proteus 的 图 表 仿 真(Analogue Analysis)与Matlab Simulink 仿 真。仿真软件分别为Proteus8.13 与Matlab R2014B。电机参数:表贴式永磁无刷直流电机,电机反电势为梯形波,相电阻R=2.85Ω,相等效电感Ls=0.0085H,阻 尼 系 数B=0.0008N.m.s/rad,转 动惯 量J=0.0008kg.m2,相 绕 组 的 磁 链flux=0.175Wb,极对数pn=4,滞环宽度HB=0.1,电源电压Udc=310V。仿真条件:额定速度Speed=1000r/min,初始时刻负载TL=3N.m,0.05s 时负载TL=1N.m。速度环PI 控制参数:Kp=1,Ki=0.06。
3.1 基于图表仿真
基于图表仿真的方法:是在Proteus 界面的工具箱中选择ANALOGUE 分析工具,在原理图上直接绘制仿真图表,然后添加需要的探针信号标识,便可以运行图表仿真。这种图表仿真,位于原理 图上,有助于快速捕捉原理图设计意图,比较直观、方便。这里采用了四种图表仿真,仿真结果如图6 所示。
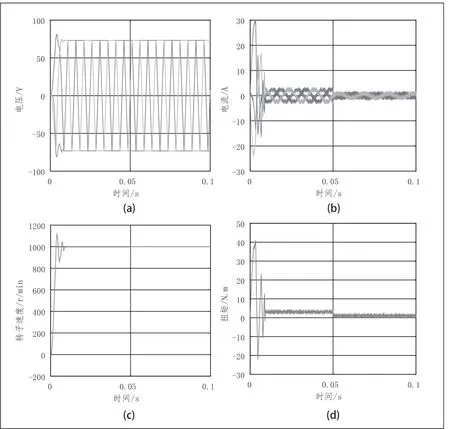
图6 Proteus 仿真结果图
图 中,(a)、(b)、(c)、(d) 分 别 为反电势、电流、转速、力矩的波形图。从仿真结果可以看出,在0~ 0.1s 仿真期间,各个阶段的瞬时仿真细节展示比较清晰,比文献[3]提到的相应波形更加细致,充分反映了电机的瞬时运行状态,以及运动规律。从控制效果看,启动时电机虽然带着TL=3N.m 的负载转矩,但是0.01s 后就达到了1000r/min 的额定转速;0.05s 后,负载转矩降低到TL=1N.m 时,电机也能维持在额定转速,说明滞环电流控制满足了电机控制要求,从而验证了BLDCM 仿真模型的正确性。
3.2 Matlab 仿真
Matlab 的仿真引用了参考资料[8]提供的仿真方法,Simulink 控制框图如图7 所示。虽然框图中电机的模型图标是PMSM 电机,但实际上,里面的参数都按这里的仿真条件设置成了BLDCM 电机模型。

图7 控制框图
该仿真模型的仿真结果如图8 所示。

图8 Matlab 仿真结果图
图中,(a)、(b)、(c)、(d)分别为反电势、电流、转速、力矩的波形图。整体上看,Simulink 的仿真结构与前面的仿真结果基本一致。下面,对这两种结果进行比对分析。
3.3 结果分析
从Proteus 的图表仿真结果与Matlab Simulink 仿真结果对比发现,BLDCM 的反电势波形、电流波形、速度波形、力矩波形的形状分别相同。反电势波形,在0.01s 之内,波动范围均是-80V~+80V。0.01s 之后,都是相同幅值的标准梯形波。电流的波形,在0.01s 之内波动比较大,都是在-25A~30A 之间,0.01s 之后都是相同幅值的马鞍波形。转速波形,在整个仿真周期都是一致的,在0.01s 之前,出现了10%的超调量,但是,迅速进行了调整,之后就稳定在额定转速1000r/min。力矩波形,在0.01s 之前波动较大,均处于-25N.m~+40N.m之间,0.01s之后,力矩输出曲线相对平坦,且与负载的阶梯变化保持一致。显然,这两种仿真方式都成功获得了相同参数BLDCM 的仿真结果,四种波形详细的展示了相同的运行状态。
为了进一步了解两种软件的仿真差异,以速度波形为分析对象,两种波形做个相减操作,让图8 数据减去图6 数据得出差值,结果如图9 所示。

图9 速度差值图
图中,(a)为全轮廓图,(b)为放大图。在0.01s 之前,速度差值较大,波动范围为-135r/min~+115r/min;0.01s 之后,差值大幅度减少,当负载转矩为TL=3N.m 时,稳定在-0.4r/min~+0.3r/min 之 间,当 负载 转 矩 为TL=1N.m 时,稳 定在-0.25r/min~+0.1r/min 之间。显然,在达到额定转速之前,两种仿真结果之间的差值比较大,到达额定转速之后,差值变得较小,负载转矩越变小时,差值也变小。出现这样的情况,其中的原因涉及到软件的底层代码、采样精度、收敛算法等等因素,可能需要相关的软件开发人员才能解答清楚,有待后续进一步研究。不过,这点差异对于研究电机的控制算法影响不大,仿真结果依然可以充分展示电机的运行规律。
4 结论
通过Proteus 与Matlab 两种软件的仿真试验研究可以看出,Proteus搭建的仿真模型,其仿真结果充分展示反电势、相电流、转速、力矩的变化细节,与Matlab 的仿真结果在变化趋势、波动幅度方面基本一致,证明了基于Proteus 建立的BLDCM 仿真模型的正确性。该模型展示的电机仿真细节比系统自带的电机模型更详尽,在一定程度上可以媲美Matlab 软件的仿真效果。因此,这个BLDCM 模型完全可以作为Proteus 软件在BLDCM 仿真方面的有效补充,值得推广应用。
