光伏发电系统逆变器并联运行谐波环流的抑制研究

席盼博

（中核汇能（甘肃）能源有限公司，甘肃兰州，730070）

0 前言

随着世界工业化文明程度的提高，各国对能源的依赖程度越来越高，而对能源的依赖当中尤其以煤炭、石油和天然气为主，正因于此，所以造成了资源越来越匮乏和能源消耗带来的环境污染等问题。为了保证经济发展和人们对于能源的需求，我们需要新的能源来替代传统能源进行发电,太阳能是现在各国公认的最满意的清洁能源，其具有经济、环保等优点[1]。

文献[2]主要是对LC 滤波器的参数进行确定和对传统下垂控制的方案进行改进，使得下垂控制的适用环境进一步扩大，但是对于系统谐波环流的抑制效果并不是特别优越，特别是在系统出现严重谐波的时候，其滤波环节的滤波效果较差；文献[3]主要讨论了传统下垂控制当中由于逆变器线路当中线路出现不匹配时，造成系统的不稳定和引起无功功率不能进行均分的问题，通过引入虚拟复阻抗和将逆变器输出端和母线端的电压偏差量作为反馈量对传统下垂控制进行改进，此研究尽管对系统稳定性能有所改善，但是对于非线性负载出现对于系统的影响并没有极大的改善；文献[4]主要是对三相孤岛模式电网当中不对称负载出现对于系统电压稳定性的研究分析，采用分层优化控制对系统的稳定性能有一定的改善，但是改善效果还是存在一定的缺陷，不能对谐波产生很好地抑制。

因此，对逆变器并联系统的拓扑结构和其控制策略进行研究分析，对其拓扑结构和控制策略进行一定的改进和优化会使得光伏发电逆变器并联系统实现更好地功率均分控制，同时会使得光伏发电逆变器并联系统的整体性得到很大的改观 ，提高系统带负载的能力，对于光伏发电和能源发展需求具有重要的意义。

1 光伏发电逆变器并联运行原理

1.1 逆变器并联运行系统的拓扑结构和等效模型

两台三相逆变器并联当中的电压型拓扑结构如图1 所示，其在现代发电系统当中扮演着极其重要的作用，其拓扑结构当中的参数约束和单相的基本相同，主要滤波环节还是采取LCL 进行，输电传送距离是其重要的一个影响因素[5]。

图1 两台三相变压型逆变器并联系统拓扑结构

对两台逆变器并联的模型进行建立与分析，等效模型如图2 所示。

图2 逆变器并联系统的等效模型

第一台和第二台逆变器的输出电压分别用U11φ∠ 、、U2∠φ2来表示，电流矢量用i1和i2来表示，输出的电压矢量以u3进行表示，两台逆变器的输出阻抗分别以R0、X0、R1、X1进行表示，公共负载用Z表示[6]。根据图2 可得逆变器并联系统的等效模型为：

在实际当中，并联系统输出端的电抗值跟电阻值相比起来，其值要大的多，继而可得R0＜＜X0,R1＜＜X1,因此可将式(2)改写为下式：

由以上的表达式，我们可以更加直观的看到，在负载电流的主要成分当中主要包括两部分，一部分是系统自身的负载电流，另一部分是并联逆变器之间的环流。根据并联的特点，正常运行状态下，系统的负载电流在其并联的逆变器中是均分的，唯一有差异的就是环流，因为环流的大小取决于并联逆变器的状态，主要受其输出端电压的相位和幅值影响[7]。

1.2 逆变器并联运行谐波环流的分析

根据环流的一般定义和式(3)，可得到下式：

由式(2)，我们可以得到谐波环流产生的主要原因：

由式(6)可得，组成环流的两部分:输出端的电压和等效的阻抗皆会因为其自身的变化来影响谐波环流。

由式(7)可得，在输出端的电压保持相等时，等效的阻抗单独变化也会影响谐波环流。

由式(8)可得，此时的谐波环流将会受阻抗和电压的共同影响。

通过上面的分析，输出端电压和线路当中的阻抗是影响谐波环流的关键因素。

2 LCL 滤波器的设计

2.1 电路中电感的规划

在滤波电路中，电感的取值下限值一般都是由电路中的电流纹波来进行决定的，一般在额定电流中纹波电流会限定在10%～20%左右，在本论文中取其上限值20%。各个参数的简介如下：I1代表电流的额定数值，V1代表母线侧的直流电压数值，V是电网侧的电压有效数值，ω代表来自电网侧的基波的角频率，f代表电网侧的频率，f1代表在实际运行过程中器件开通与关闭的次数。

设计的电感的约束条件为：

2.2 电路中电容值的规划

电容值在实际的规划当中是按照其与电路当中的总谐波失真呈现反比的关系进行规划，而在实际的运行当中，电容又会对无功进行产出，进而电容的规划又与其无功的产出情况呈现正比的关系。在实际的并联系统中，对系统的要求是：其功率因数不应过小，因此对电容的要求是：其对无功的吸纳控制在5%以下。

电路的无功可以表示为：

起到滤波作用的电容C 满足的要求为：

2.3 电路中对于滤波环节的约束

对于滤波环节谐振频率约束：

根据电容的规划要求可得：

由所归纳的要求和L1/L2=10 的约束，本次滤波器的参数选择是：L1=20mH，L2=2mH，C=22μF。

对其要求频率的验证如下：

具体参数为：V=220V，V1=600V，W=100п，P=20kW，f=50Hz，f1=20kHz。

根据L1=20mH，L2=2mH，C=22μF 可得：

经验证符合谐振频率要求，进而所规划的滤波环节符合要求。

3 改进后的下垂控制算法

根据传统下垂控制特点，当系统间的连接阻抗完全是纯感性时其发挥的效果是最好的。当系统间的阻抗是非纯感性时，其效果就就会大幅缩减。为了解决系统连接阻抗为其他形式阻抗时控制出现的问题，需要对传统的下垂控制进行改进。通过对传统下垂控制的分析，我们得出在系统间连接阻抗中感性多一点的时候，电压的幅值受无功影响较大，电压的频率受有功影响较大；当系统间的连接阻抗中阻性较多时，电压幅值受有功影响较大，电压频率受无功影响较大。基于此分析，可以建设A=R/Z,B=X/Z对由于连线阻性和感性的存在对逆变器端的输出电压的频率和幅值的干扰程度。基于此，对传统的下垂控制的表达式改进如下：

上式中的m，n，m1，n1表示的是逆变器端的输出电压的频率和幅值对应的有功和无功的下垂系数。改进后的下垂控制系数可以参照传统下垂控制系数的获取，对各逆变器间的连接阻抗进行假设Z1=Z2=Z由于在分析中得出，φi一般较小，所以可令cosφi≈ 1。在系统间的连接阻抗是纯电阻特性时，并联的逆变器输出端的功率表示如下：

由此式得出无功的下垂系数：

由上式可以获得有功的下垂系数如下：

当并联系统之间的连接阻抗属性为纯电感时，按照以上方法可得：

4 逆变器并联系统仿真分析

4.1 实验平台系统搭建

为了更好地验证所提策略的实用性和科学性，在SIMULINK 仿真平台进行LCL 滤波环节的下垂控制系统模型搭建[8]如图3 所示。

图3 LCL 滤波环节加下垂控制模型

4.2 仿真结果

通过仿真系统可以看出通过对LCL 环节的设计改进和下垂控制的改进，系统可以更好地解决谐波环流存在的问题，对故障下非线性元件的出现给系统造成的冲击和危害可以起到一定的保护作用。系统中功率变化如图4 所示，加入滤波和无滤波的有功、无功变化如图5、6 所示，系统无功增加后电压和电流的变化如图7 所示，系统突加非线性负载的有功、无功和频率的变化如图8、9 所示。

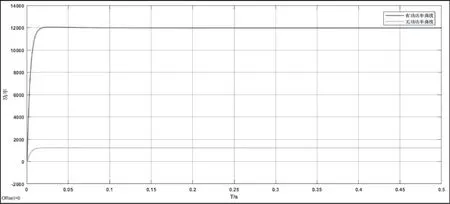
图4 系统中无功和有功曲线图

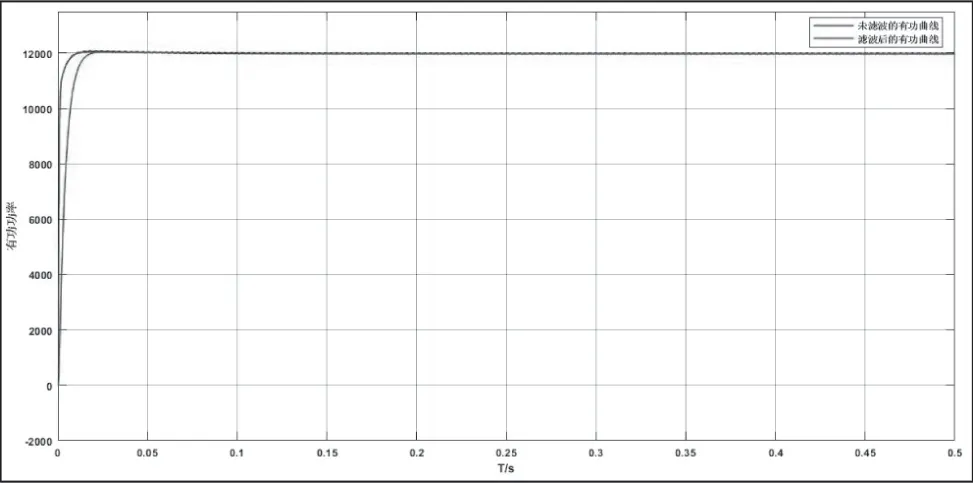
图5 系统中无滤波和有滤波的有功曲线对比

图6 系统中无滤波和有滤波的无功对比曲线

图7 系统中无功增加后的输出电压、电流波形

图8 系统中突加负载的有功、无功曲线

图9 系统中突加负载的频率变化曲线

5 总结

通过实验结果分析可得，在拥有下垂控制和LCL 滤波环节的系统中，系统输出的无功和有功曲线会更加平滑的稳定在负载周围如图4；系统的有功和无功在经过滤波环节之后其波形更加光滑如图5、6；系统的三相输出电压和电流波形更加光滑如图7；系统在突加非线性负载之后，在LCL滤波环节和下垂控制的双重机制之下，输出的有功功率、无功功率和频率，尽管在一定范围内会增加，但是会被控制在允许范围之内，抑制了谐波环流，系统更加稳定如图8、9。通过对设计改进的滤波器和下垂控制的验证，得出其对并联系统出现的谐波环流可以起到很好的抑制作用，可以更好地保护系统，使系统的稳定性更好，滤波效果更加优越，同时也更好地验证了这种成比例调整滤波环节和控制环节的科学性。