基于生成对抗网络的脑电波去噪处理研究

文 斗，杨 青，王亚群，李 晨，李 铭

（1.华中师范大学 计算机学院；2.华中师范大学人工智能与智慧学习湖北省重点实验室；3.国家语言资源监测与研究网络媒体中心，湖北 武汉 430079）

0 引言

脑电波（Electroencephalogram，EEG）是一种使用电生理指标记录大脑活动的方法［1］。其记录大脑活动时的电波变化，是脑神经细胞的电生理活动在大脑皮层或头皮表面的总体反映。脑电波信号对于神经科学研究和临床应用非常重要，例如脑—机接口（BCI）［2］、神经系统疾病诊断［3］等。但是采集到的信号通常包含生理噪声和外部噪声［4］，其中生理噪声包括眼部噪声［5］、肌源性噪声［6］以及少见的心源性噪声［7］等。

眼电（EOG）和肌电（EMG）信号是EEG 中最常见的噪声源。EOG 源于眼球运动，如眨眼和滚动，而EMG 源于大脑周围肌肉的运动。因为几乎不可能防止眼睛眨眼和脑周围肌肉群运动，所以这些噪声在脑电信号中时常出现。因此，需要准确地将这些噪声信号去除，以获得相对干净的脑电波信号，从而快速、准确地进行诊断。

目前，大多数去除脑电信号伪影的方法可以分为两种，第一种方法是对于具有不同频谱分布的脑电信号和伪影，使用傅里叶变换或小波变换将信号从时域变换到频谱域，然后过滤与伪影相关的频谱分量。去噪后的信号可以通过傅里叶逆变换或小波逆变换进行重构，有多种滤波器可用于脑电信号去噪，如维纳滤波器［8］和卡尔曼滤波器［9］等。然而，由于伪影与脑电信号频谱［10］之间的重叠，伪影无法完全消除，进行滤波后神经信息可能丢失。

另一种方法是将信号从原始空间转换到新空间，从而使信号和噪声在新空间中可分离，例如自适应滤波器（Adaptive filter）［11］、希尔伯特—黄变换（HHT）［12］、经验模式分解（EMD）［13］等。以上方法主要使用线性变换，所以需要额外的信息或者严重依赖于先前的假设。例如Adaptive filter 需要记录噪声信号作为参考，如果未正确提供参考信号，则降噪性能可能很差。基于HHT 的伪影去除方法的假设是伪影分量具有与其他分量不同的时频特征，脑电信号被自适应地分解为固有模式函数（IMF）。HHT 输出IMF 的瞬时频率（IF），增强了时频信息［12］。如果IMF 之间存在较大距离，则将其选作噪声分量并移除。但由于距离阈值是手动选择的，导致算法的稳定性不强。基于EMD和基于ICA 的方法都将多通道EEG 信号分解为多个分量，然后根据特定标准去除噪声相关分量，但仍然不能解决先前假设的局限性，例如EEMD-ICA 中两个自相关阈值的选择是在不同场景下根据经验确定的。

然而，用深度学习进行脑电波去噪的方法目前还是一个新兴的方法。在EEG 去噪方面，目前只发现少量基于深度学习的研究，例如文献［14-17］设计的模型提供了与传统去噪技术相当的脑电去噪性能，但存在一个问题，文献［15-17］研究针对的数据集不同，无法将模型作统一的比较。而文献［14］提供了一个用于脑电去噪的基准数据集（EEGdenoiseNet），该基准数据集由大量用于训练与测试深度学习模型的干净单通道EEG、EOG 和EMG 信号时段组成，同时文献［14］也设计了一些基准网络，例如全连接网络（FCNN）、简单卷积网络、复杂卷积网络和递归神经网络（RNN）对该数据集进行评估比较。在文献［14］的数据集基础上，文献［18］设计了一种消除脑电肌肉伪影的卷积神经网络模型Novel CNN，通过与4 个经典网络进行比较，肌源性去噪性能得到了提升；文献［19］设计了一种2-D Transformer 模型对基准数据集（EEGdenoiseNet）去除脑电噪声；文献［20］设计了GAN-LSTM 模型对基准数据集（EEGdenoiseNet）去除脑电噪声；文献［21］设计了类似于encode 和decode 网络的DeepSeparator 模型对基准数据集（EEGdenoiseNet）去除脑电噪声。文献［14-19］和文献［21］所设计的深度学习去噪模型虽然取得了一定的去噪效果，但其仍具有局限性。其模型训练方法偏向于数据特征提取，特征提取往往对输出维度小于输入维度的模型可起到比较好的收敛效果。但对于去噪来说，模型的输入与输出有着相同的维度，所以上述模型的去噪性能并不能得到很大改善。

本文在前人的研究基础上，设计了基于生成对抗网络（Generative Adversarial Networks，GAN）的EEG 去噪模型（GAN-1D-CNN）。模型与文献［20］设计的GAN-LSTM 网络都是基于GAN 网络的，但GAN-LSTM［20］的生成器采用的是可以学习长期依赖信息的长短期记忆网络（LSTM），其属于RNN 回归型网络，经常用于时序数据训练，并且有了一定的记忆效应。但对于去噪而言，完全采用1D-CNN结构的Novel CNN 已表现出比GAN-LSTM［20］更好的肌源性去噪性能。因此，在GAN 网络中，本文选用1D-CNN 为生成器的基础结构进行实验，同时设计了新的网络生成器和判别器，并引用了新的损失函数计算方式［22］。改进的GAN 模型在EEGdenoiseNet 数据集上使用不同信噪比（SNR）和模型评价指标（时域相对均方根误差、频域相对均方根误差和相关系数）进行分析，同时对应用该数据集的最新模型进行了比较。实验结果显示，改进的GAN 模型在EEG 去噪性能上得到了增强。

1 相关理论

GAN 是深度学习领域一个无监督状态的生成模型，被用来生成一些不需要专业领域知识的数据，其由Ian 等［23］于2014 年10 月 在Generative Adversarial Networks中提出。GAN 由判别器D 和生成器G 组成，两者通常是两个神经网络模型，被锁定在由式（1）中目标函数定义的博弈中。

其中，x 是真实样本集合pdata 中的一份样本，z 是多组随机噪声下的一组分布，D（x）的输出维度为1，值的范围在0～1 之间。G（z））为生成器生成的样本，D（G（z））是判别器对生成器生成数据的辨识度。如果生成器的生成能力越来越强，超越了判别器，判别器已经辨认不出真假，则V（G，D）将是一个极大的负值。相反，如果生成器能力太弱，对判别器而言D（G（z））值总是接近1，则V（G，D）将无限逼近0。也即是说，V（G，D）的值不断上下浮动，上述过程展现了生成器与判别器的对抗过程。

生成器尝试最大化欺骗判别器，其目标是希望能够学习到真实样本的分布，从而可以随机生成以假乱真的样本，判别器旨在从生成器生成的样本中识别真实样本。整个系统可以用反向传播进行训练，反向传播过程如下：生成器生成的数据和真实样本被同时输入到判别器进行训练，计算损失函数后，进行梯度计算和判别器梯度更新；此时生成器只计算了梯度，并未更新，生成器生成的数据再次被输入到判别器中，此时生成器只计算并更新梯度，但判别器只进行计算，没有更新梯度；如此反复，直到得到满意的结果，取最终需要的生成器作为生成模型。在训练或生成样本期间，不需要任何马尔可夫链或展开的近似推理网络，所以GAN 常被用于超分辨率任务以及图像生成、语义分割等领域。

2 GAN-1D-CNN设计

2.1 设计思想

GAN 最初被运用于图像生成和图像合成，近年来在序列数据生成、插补和数据扩充领域得到了快速发展。在文献［24］中，GAN 被用于EEG 生成和增强。然而，很少有研究探索用于时间序列去噪的GAN，尤其在涉及EEG 数据的情况下。文献［25］设计了非对称GAN，用于去除EEG时间序列数据的噪声，该时间序列去噪模型使用未配对的训练语料库进行训练，不需要关于噪声源的信息。文献［26］使用GAN 对小鼠脑电图进行去噪，该训练过程需要一组嘈杂的信号和一组清晰的信号。虽然这些方法降低了EEG 信号中的噪声，但其既不能去除特定的伪影，又不能提供动态信噪比的可靠定量证据。

本文设计的GAN-1D-CNN 模型由生成器和判别器组成，相比文献［20］设计的GAN-LSTM 网络中的生成器，模型使用擅长提取一维空间特征的卷积神经网络（Convolutional Neural Network，CNN）替换掉可以学习长期依赖信息的长短期记忆网络（LSTM），使网络的一维空间特征提取能力得到增强。模型处理流程如图1 所示。肌源性噪声（EMG）和眼源性噪声（EOG）与原始脑电波片段（Raw EEG）混合，生成含有噪声的脑电波片段（Noise EEG）；将含有噪声的脑电波片段输入到GAN-1D-CNN 模型的生成器（Generator），生成器输出去噪后的脑电波（Denoised EEG），再将原始脑电波片段和去噪后的脑电波片段分别输入到判别器（Discriminator）通过得分辨认真伪；通过判别器的不断纠正，使生成器的去噪输出与原始脑电波片段更接近。训练好的模型使用模型的生成器即可对样本进行去噪。

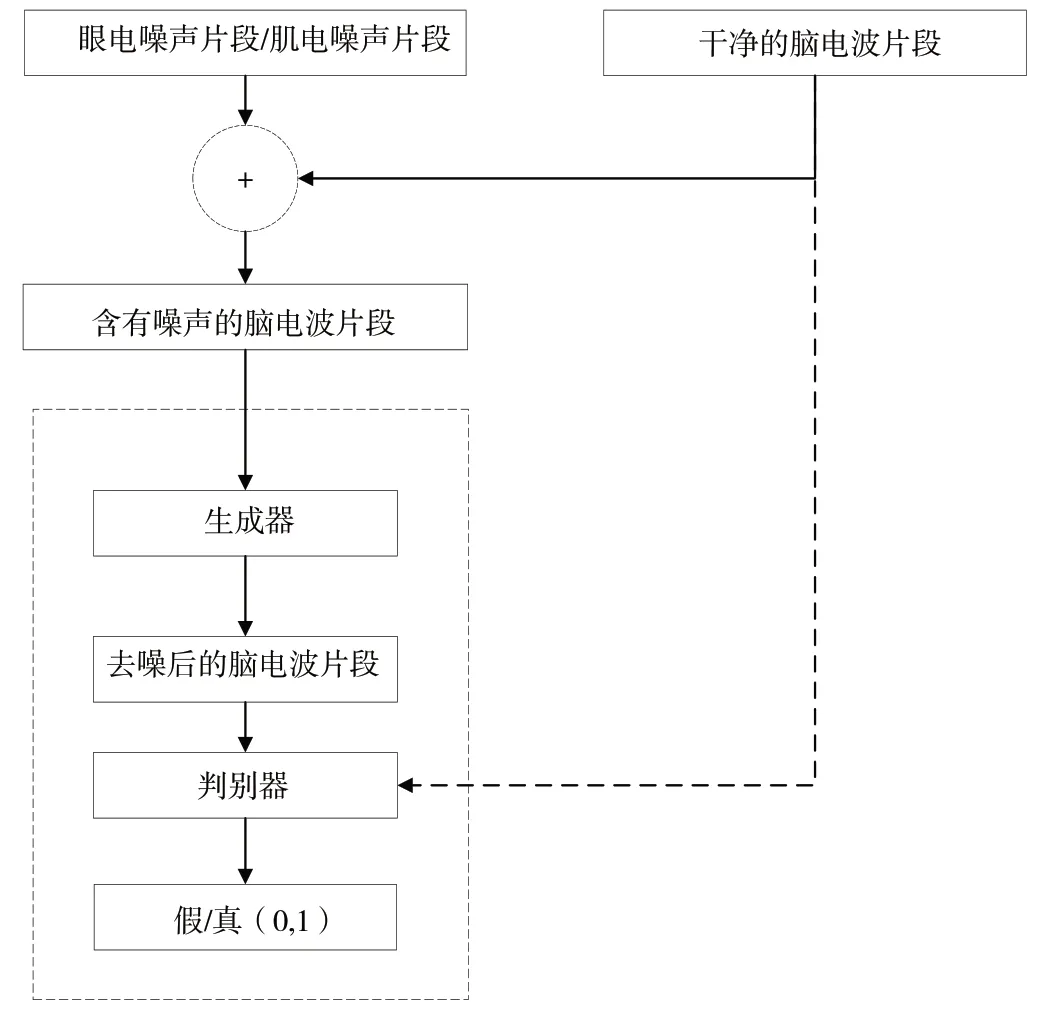
Fig.1 Flow of model processing图1 模型处理流程

2.2 生成器与判别器结构

GAN 的生成器网络由一个核心的神经网络层堆叠而成，模型的神经网络层参考文献［18］中Novel CNN 的相关参数。在网络每一层的参数更新过程中，会改变下一层输入的分布。神经网络层数越多，表现得越明显，从而会导致内部协变量偏移问题。为了使每一个神经层的输入分布在训练过程中保持一致，本文在Novel CNN［18］基础上引入批量规范化层（Batch Normalization，BN）。同时考虑到每一层神经网络存在输入负值的问题，引入Leaky Relu 激活函数替代Relu 激活函数。每个神经网络块（Block）包含两轮一维卷积、归一化、LeakyRelu 线性激活层和池化处理过程。生成器网络模型架构如图2 所示，卷积核参数如表1 所示。生成器的卷积核参数一共有7 个，卷积核个数分别是（32、64、128、256、512、1 024 和2 048）。卷积核大小为1*3，步长为1，填充程度设为1。同时通过一维平均池化层逐渐降低脑电信号的采样率，使输入为1 024 维度的单通道EEG 经过卷积神经网络特征提取后依然保持输出维度为1 024。

判别器网络采用一个核心的神经网络层堆叠而成，判别器网络参考了生成器网络的设计，但每个神经网络块（Block）包含一轮一维卷积、归一化、LeakyRelu 线性激活层和池化处理过程。判别器网络模型架构如图3 所示。本文在设计判别器时考虑到生成器和判别器之间的对抗过程，因此两者训练时的学习速度应该相当。如果判别器能力太强，会导致生成器无法继续学习；如果判别器能力太弱，会导致生成器最终的生成效果差。由于判别器的判别任务与生成器的生成任务相比更加简单，所以在设计判别器模型时减少了模型卷积核的相关网络参数。卷积核参数如表2 所示。卷积核大小为1*3，步长为1，填充为1，卷积核个数分别是（16、32、64、128 和64），再通过一维平均池化层，最后平展维度为2 048，连接一维的输出层。输出层使用Sigmoid 函数，使分布符合0～1（3.3节将作解释）。

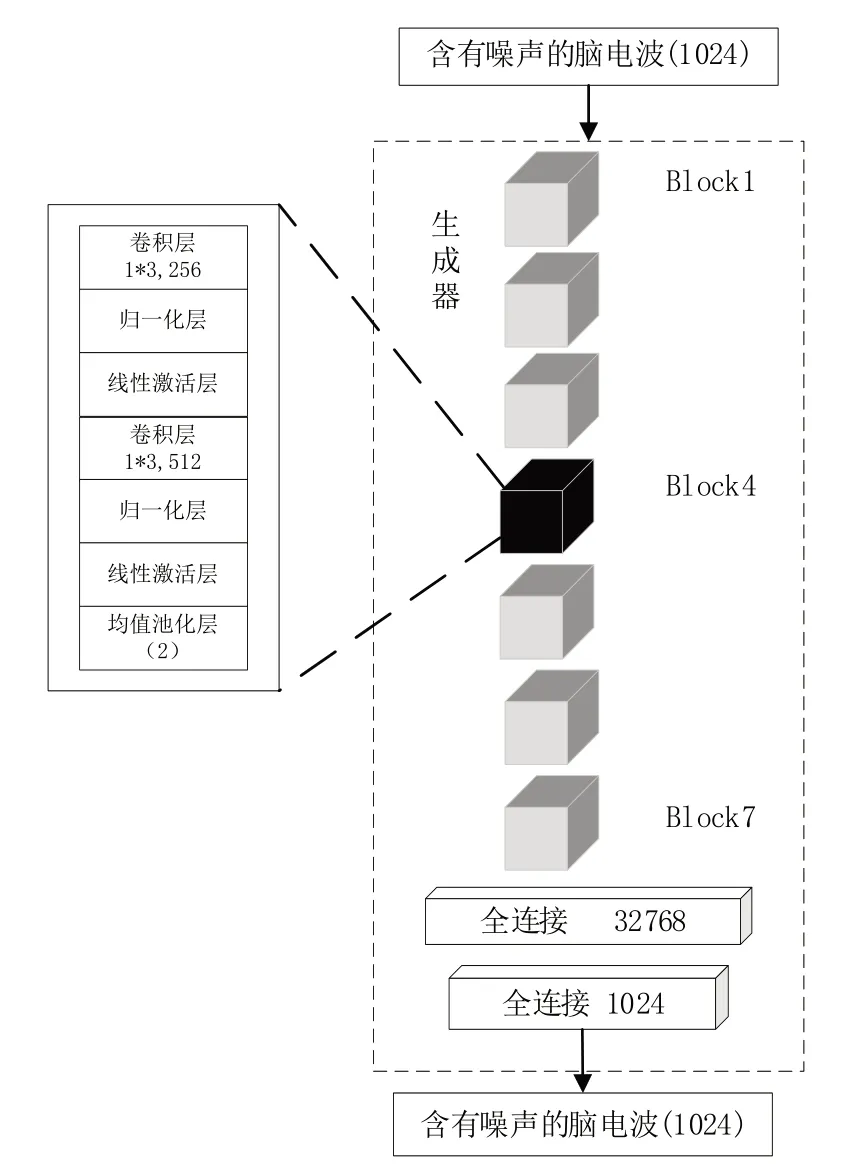
Fig.2 Generator model图2 生成器模型

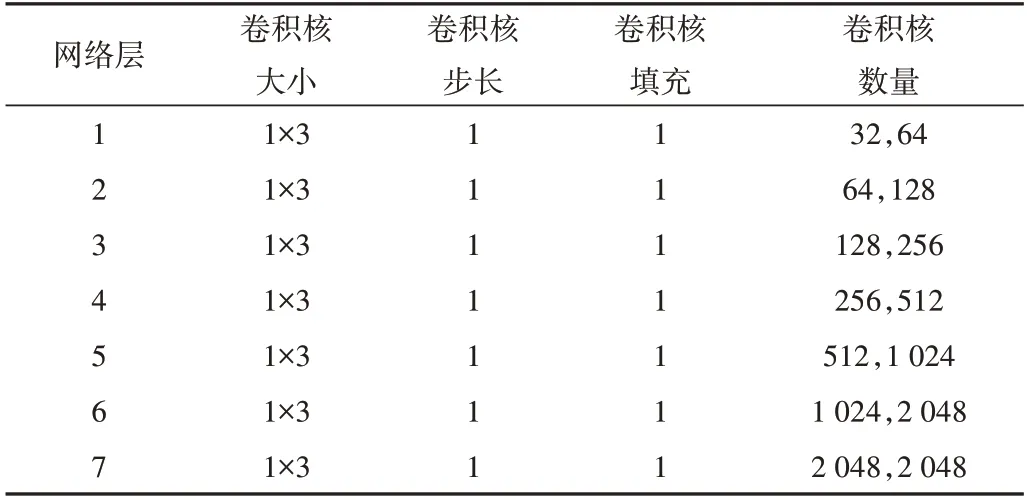
Table 1 Kernel parameters of generator convolution表1 生成器卷积核参数

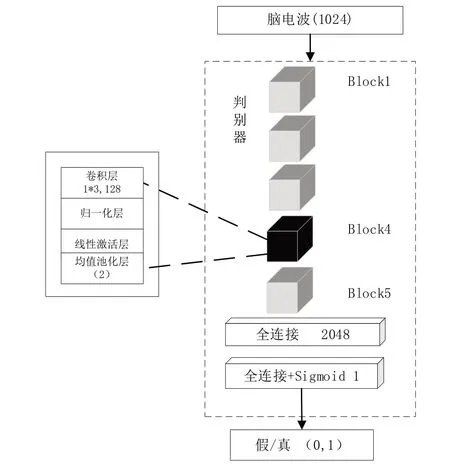
Fig.3 Discriminator model图3 判别器模型

Table 2 Parameters of discriminator convolution kernel表2 判别器卷积核参数

2.3 模型损失函数

模型损失函数计算流程如图4所示。

模型有两个损失函数。第一个损失函数是判别器的损失函数，具体计算过程如下：含有噪声的EEG 数据（S）被输入到生成器，生成器的输出G（S）可以是经过去噪后的数据，也可以是仍含有噪声的数据。G（S）和与之对应的干净的EEG（Y）会被输入到判别器中，其目的是使判别器具有对噪声EEG 和干净EEG 进行分类的能力。Y 和G（S）被输入到判别器后，D（Y）和D（G（S））分别为判别器对应的输出，其可以反映生成器输出的EEG 数据是否干净。判别器可以看作是一个二元分类器，判别器的损失函数如式（2）所示。该式取决于D（Y）和D（G（S）），损失值越小，判别器辨别噪声数据的能力越强。如果判别器的输出值接近1，则数据是相对干净的，否则判别器会认为数据相对含有噪声。

另一个损失函数是生成器的损失函数，具体计算过程如下：G（S）被输入到判别器后，判别器输出D（G（S）），在传统的GAN 网络中，生成器的损失函数由式（3）所决定，其大小取决于D（G（S））的输出值。但为了使样本S 在除噪声后与干净的Y 更拟合，同时尽可能保留原始信息，这里引入一个新的损失函数，计算方式如式（4）所示。生成器的损失函数不仅由D（G（S））决定，而且由G（S）和Y 的均方误差（MSE）决定。

在与判别器博弈的过程中，生成器的损失函数将逐渐趋近平衡。判别器损失函数的数值逐渐下降，则说明生成器的输出与真实样本更逼近。模型训练时，在式（4）中，设α为0.5，β为0.5。

3 实验与分析

3.1 数据集

实验中使用的数据集是用于深度学习去噪研究的开源基准数据集EEGdenoiseNet，该数据集包含4 514 个干净的单通道EEG 片段（EEG 片段长度为1 024）、3 400 个眼部伪影片段和5 598个肌肉伪影片段［14］。样本片段的电位和功率谱密度情况如图5所示。

对于EEG 片段，数据集包括52 名参与者执行真实与假想的左手和右手运动任务，在512 Hz 采样频率下同时记录的64 通道EEG。为了获得干净的EEG，64 通道的EEG信号通过ICLabel 工具去除EEG 伪影，然后将纯脑电信号分割成2 s 的一维段。为了确保该数据集的通用性，EEGdenoiseNet构造了具有单通道脑电信号的数据集。

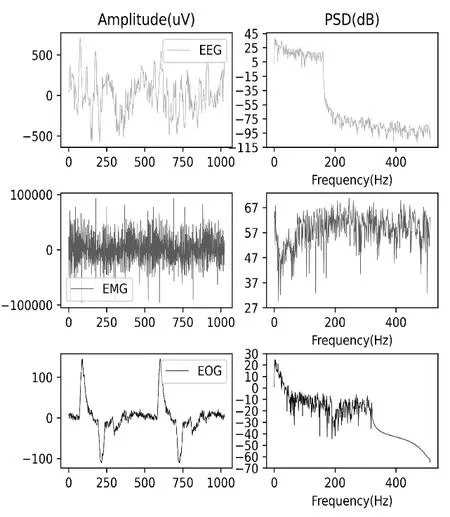
Fig.5 Fragments of experimental samples图5 样本片段

对于眼伪影段（EOG），EEGdenoiseNet 使用了具有额外EOG 通道的多个开放存取的EEG 数据集，EOG 信号被分割成2 s 的一维段。对于肌源性伪影段（EMG），使用的是面部肌电数据集。选择面部肌电图是因为其是肌源性伪影的主要来源，原始肌电信号经过带通滤波，将肌电信号以512 Hz的频率重新采样，得到了一段2s的肌电片段。

3.2 数据预处理

本文使用EEGdenoiseNet 的数据生成干净的脑电信号和噪声脑电信号，用于训练和测试本文所设计的神经网络模型。对EEGdenoiseNet 的具体处理方式如下：4 514 个EEG 和5 598 个EMG 记录被用来模拟带有肌源性伪影的噪声EEG，由于EMG 片段多于EEG 片段，本文参考文献［14］的基准网络实验随机重复使用一些EEG 片段和剩余未使用的EMG 片段混合，产生新的含EMG 噪声的EEG，从而扩充数据样本，但又保持输入到模型的样本的差异性。将EEG 数量增加到5 598 个，获得了5 598 对EEG 和肌源性伪影，同时将5 598对数据随机打乱。

采用从-7～2dB 的10 个不同的信噪比（SNR），计算方式如式（5）所示。其中，x 为真实EEG 信号，n 为肌源性噪声或眼缘性噪声。在式（6）中，y表示EEG 和肌源性的混合信号，x 表示原始干净的EEG 信号。通过式（6）的线性混合，将4 478 对EEG 和肌源性伪影（EMG）数据随机组合10次，至此数据被扩充10 倍。均方根（RMS）值定义如式（7）所示，其中gi代表脑电信号每一时刻的电位。

在模型训练和验证过程中，80%的数据用于训练，20%的数据用于验证。包含肌源性噪声的脑电信号和原始脑电信号对比数据样本如图6（a）所示。同理，将3 400个EEG 片段和3 400 个EOG 片段利用-7～2dB 信噪比使用式（6）的线性混合，将包含眼部伪影的EEG 数据扩充了10倍。其中，80%的数据用于训练，20%的数据用于验证。包含眼源性噪声的脑电信号和原始脑电信号对比数据样本如图6（b）所示。

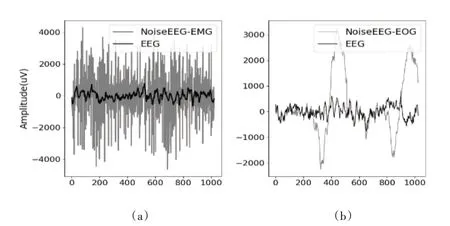
Fig.6 Comparison between EEG and noise EEG图6 原始EEG与包含噪声的EEG对比

在输入到模型之前，为了使神经网络在EEG 大范围的电位振幅下仍具有很好的泛化性，通过式（8）将EEG 信号除以其标准偏差作归一化操作。其中，x为真实EEG 信号，y 为噪声EEG 信号，对x 和y 分别进行归一化处理。将归一化的污染脑电片段输入到模型的生成器，然后输出去噪后的脑电片段。将去噪后的脑电片段乘以干净EEG 的标准偏差即可进行数据复原。

3.3 实验结果

本实验借助深度学习软件PyTorch 框架实现GAN-1D-CNN 模型，使用NVIDIA Tesla V100 GPU 进行模型训练，并在Python3.7 软件环境下进行实验。数据输入批次大小为64，迭代次数为25 次，模型优化器采用 Adam 优化器，优化器梯度以及梯度平方的运行平均值系数分别设为0.5 和0.999。本文经过多次测试，当生成器的初始学习率为 2×10-4、判别器的初始学习率为3×10-5时，模型经过多次博弈训练，会实现一个相对平衡且比较好的去噪效果。为了供读者复现参考，模型基础代码已经开源：https：//github.com/wendou-wd/Denoise-EEG/tree/master。

为了将GAN-1D-CNN 与在EEGdenoiseNet 上研究的其他模型性能进行比较，本文对去噪后的数据采用3 个相同的性能评估指标［27］，分别是时域相对均方根误差RRMSEtemporal（简写为RRMSET）、光谱域相对均方根误差RRMSEspectral（简写为RRMSES）和平均相关系数CC。在式（9）-式（11）中，变量y 代表含有噪声的EEG 信号，变量x 表示y未加入噪声源之前的初始EEG 信号，f（y）表示经过GAN 网络去噪后的EEG 信号，PSD 是指对脑电信号进行功率谱密度计算，Cov 函数用于计算两个变量f（y）与x 之间的协方差，Var函数用于计算样本方差。

在以上3 项评估指标中，RRMSET 和RRMSES 值越小，代表去噪后的样本与原始样本更接近；CC 值越大，则代表去噪后的样本与原始样本相关系数高。

在去除肌源性噪声的模型训练中，模型迭代训练25次。在训练集上，判别器的损失函数值如图7（a）所示（彩图扫OSID 码可见，下同），生成器的损失函数值如图7（b）所示，去噪后的EEG 和与之对应的干净EEG 均方误差（MSE）如图7（c）所示。在图7（a）中，随着模型训练轮次的增加，判别器的损失值不断降低，显示判别器的判别能力不断增强；在图7（b）中，生成器的损失函数值不断趋近稳定，这里损失值变大是因为生成器对判别器的欺骗能力越来越强；在图7（c）中，EEG 和与之对应的干净EEG 的均方误差代表去噪后的EEG 信号与原始信号的误差不断降低。在测试集上，每次模型迭代后的时域相对均方根误差、光谱域均方根误差、相关系数变化过程如图7（d）所示。随着模型迭代次数的增加，在测试集上的RRMSET 和RRMSES值逐渐降低，相关系数（CC）增大，模型的去噪效果逐渐变好。

Fig.7 Changes in loss values of the model on the training set and its denoising effect on the myogenic noise test set图7 模型在训练集上的损失值变化和在肌源性噪声测试集上的去噪效果

同理，在眼源性噪声去噪过程中的模型损失函数值和性能结果如图8 所示。由于眼源性噪声频率与EEG 信号频率接近，眼源性去噪相比肌源性去噪更加困难。在图8（c）和8（d）中可以看到，曲线变化并没有图7（c）和7（d）平稳。

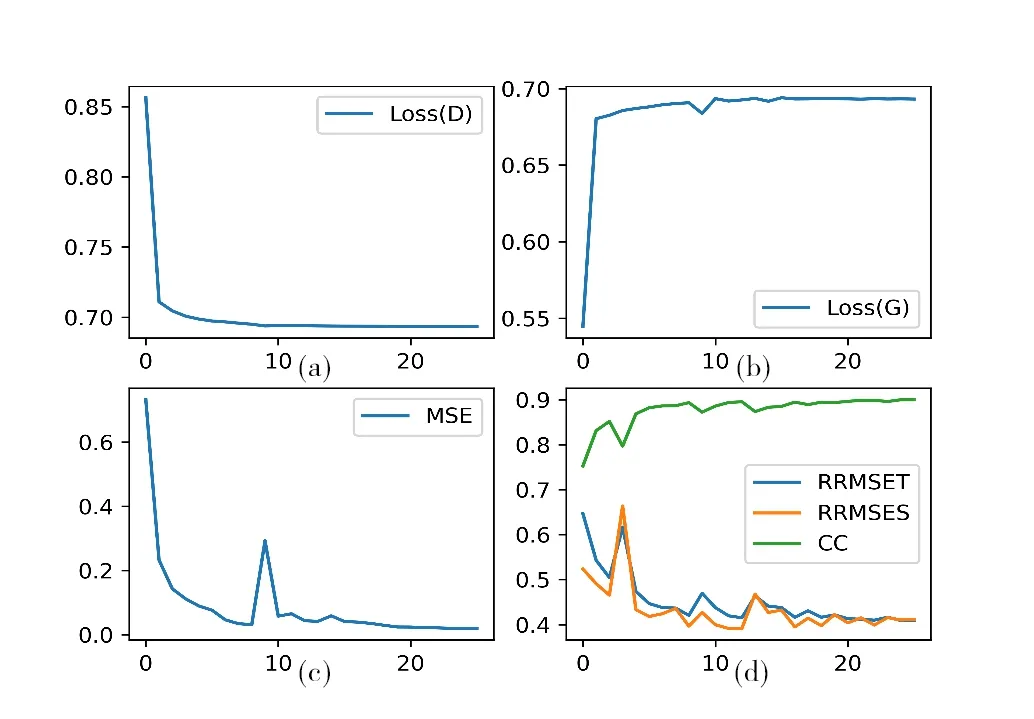
Fig.8 Changes in the loss values of the model on the training set and its denoising effect on the eye source noise test set图8 模型在训练集上的损失值变化和在眼源性噪声测试集上的去噪效果

训练好的模型对不同信噪比（SNR）的EEG 测试集数据有不同的去噪效果，实验过程中设置EEG 信噪比（SNR）的范围为-7～2。模型的去噪表现评估指标RRMSET、RRMSES、CC 分别如图9-图11所示，每个图都有6条折线，分别展示了模型在不同信噪比和不同噪声源下的平均去噪性能、最好情况下的去噪性能及最坏情况下的去噪性能。

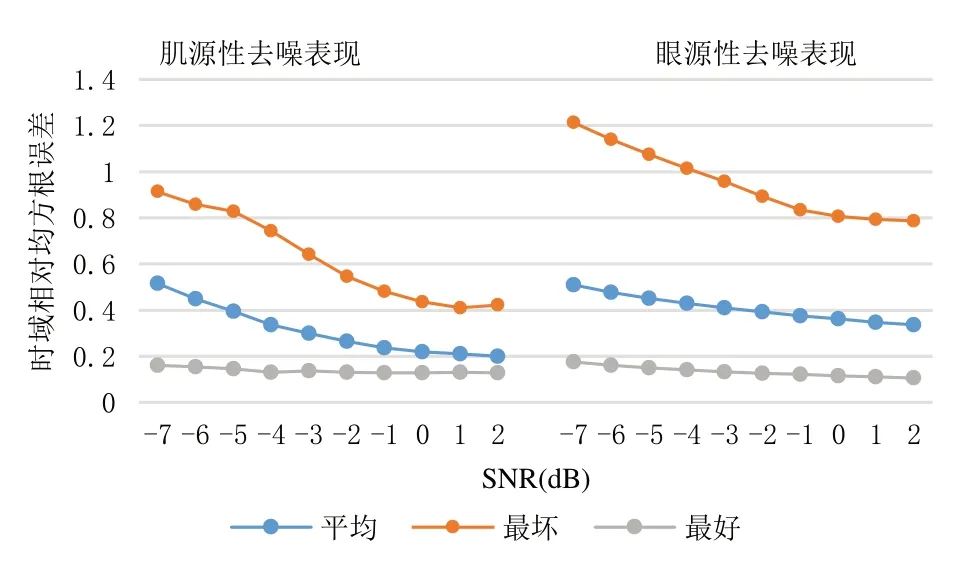
Fig.9 RRMSET performance of the model under EEG with different signal-to-noise ratios图9 模型在不同信噪比EEG下的时域相对均方根误差表现

在图9 中，左侧的3 条折线分别代表模型肌源性去噪的RRMSET 值，右侧的3 条折线则代表模型眼源性去噪的RRMSET 值。在SNR 增大的过程中，去噪效果呈现越来越好的趋势。在图10 中，左侧的3 条折线分别代表模型肌源性去噪的RRMSES 值，右侧的3 条折线则代表模型眼源性去噪的RRMSES 值。在SNR 增大的过程中，去噪效果呈现趋势与图9 类似。图11 展现了模型去噪后的EEG 和原始未加入噪声的EEG 在不同SNR 下的相关系数值，随着SNR的增大，在SNR=1 附近时，所有曲线趋于平稳，模型的去噪效果达到最佳。而且左侧肌源性去噪曲线相比眼源性去噪曲线在SNR=1 附近的收敛效果更好，说明模型在肌源性去噪上的表现优于在眼源性去噪上的表现。

Fig.10 RRMSES performance of the model under EEG with different signal-to-noise ratios图10 模型在不同信噪比EEG下光谱域相对均方根误差表现

Fig.11 CC performance of the model under EEG with different signal-to-noise ratios图11 模型在不同信噪比EEG下相关系数表现

已有的研究方法包含自适应滤波（Adaptive Filter）［11］和希尔伯特—黄变换（HHT）［12］、经验模态分解（EMD）［13］、Deep Separator［21］、EEGD Net［19］、GAN-LSTM［20］、Novel CNN［18］等，并且以上提到的模型都是基于EEGdenoiseNet数据集的性能不错且最新的EEG 去噪方法。本文将GAN-1D-CNN 模型与以上几种方法的去噪性能进行了比较，评估指标包括时域相对均方根误差（RRMSET）、光谱域相对均方根误差（RRMSES）和相关系数（CC）。由于GAN-LSTM［20］未明确给出RRMSET 和RRMSES 的值，参考相关文献模型数据，最终肌源性去噪性能实验结果比较如图12、图13所示。

图12 以直方图形式描述不同方法的RRMSES、RRMSET 差异，表明 GAN-1D-CNN 不管是在相对均方根误差（RRMSET）还是在光谱域均方根误差（RRMSET）上，模型在脑电信号上的去噪性能均有一定程度的提升，整体实验在肌源性去噪上的平均相对均方根误差达到0.292，平均光谱域均方根误差则达到0.268。

如图13 所示，GAN-1D-CNN 模型的平均相关系数达到0.945。本文选取GAN-LSTM［20］在SNR 为-2 时最好的平均相关系数为0.65，GAN-1D-CNN 模型的效果远远优于GAN-LSTM［20］，说明改进模型能有效提高去噪性能。

Fig.12 Comparison of RRMSES and RRMSET in myogenic artifact removal图12 肌源性去噪RRMSES、RRMSET比较

Fig.13 Comparison of CC in myogenic artifact removal图13 肌源性去噪相关系数（CC）比较

眼源性去噪效果比较如表3 所示，在眼源性去噪上，GAN-1D-CNN 模型去噪效果的时域平均相对均方根误差达到0.416，平均光谱域均方根误差则达到0.397，平均相关系数达到了0.894。与肌源性去噪相比，其眼源性去噪性能稍差，这与噪声的频率混合程度有很大关系。综上，改进的GAN 模型与其他模型和方法相比，不仅在肌源性去噪性能上得到了提升，在眼源性去噪上的表现也相对优异。

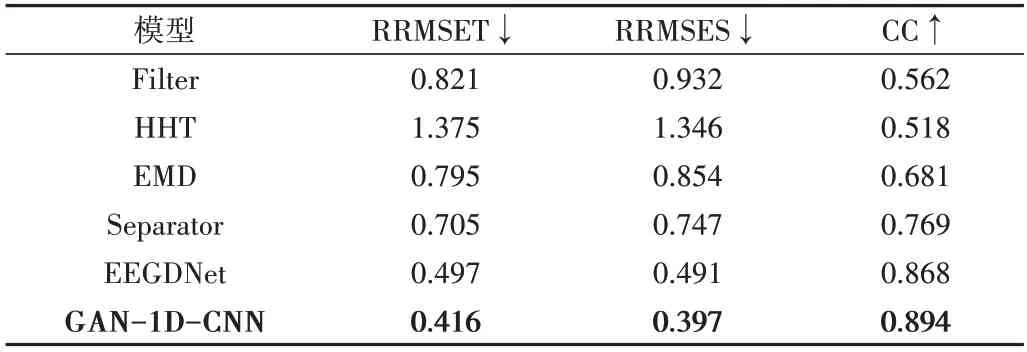
Table 3 Average performances comparison in ocular artifact removal表3 眼源性去噪平均性能比较

4 结语

在脑电波去噪领域已经有了许多相关研究，但在去除脑电波生理噪声方面，自适应滤波器、空间滤波和主成分分析等方法还不能解决先前假设的局限性和去噪后脑电信号可能存在丢失的问题。如今，深度学习技术在去噪领域已经崭露头角，但目前在脑电波去噪领域还是一个新兴的方法。准确去除脑电波中的眼部噪声和肌肉噪声是一项困难的任务。本文利用改进的GAN 网络对脑电波进行去噪研究，模型以卷积神经网络为基础，优化了GAN 网络中的生成器和判别器，同时在生成器中引入新的损失函数。实验结果表明，改进的GAN 模型对脑电波的去噪能力得到了增强，模型的相关性能指标都优于目前现有的基准数据集［14］上的去噪方法。然而，模型也有一定的局限性，例如基准训练数据集的体量对于复杂多变的脑电波信号来说还相对较少。但值得注意的是，GAN-1D-CNN 的模型架构是一种通用模型架构，该模型架构也可应用于其他一维信号的去噪处理，给其他领域的电信号去噪问题提供了解决方案。