融合预瞄特性的智能电动汽车稳定性模型预测控制研究*
2023-05-29贺伊琳杨舒凯薛启帆
贺伊琳,马 建,杨舒凯,郑 威,薛启帆
(1.长安大学汽车学院,西安 710064;2.西安科技大学电气与控制工程学院,西安 710064)
前言
随着能源与交通安全问题的日益突出,电动化与智能化成为未来汽车的发展方向[1]。其中分布式驱动电动汽车各驱动轮独立,且对控制响应速度快、精度高,易于实现底盘主动控制,分布式驱动智能电动汽车已成为汽车领域的研究热点。
现阶段,随着智能电动汽车技术的进步,其行驶速度随之提升,运行环境也更加复杂。同时,车辆本身是一个高度非线性系统,在高速行驶状态下除了受到自身动力学约束以外[2],还会受到地面附着条件、侧向风与道路曲率的影响,特别是在低附着系数的大曲率道路上行驶时很容易失稳。因此,保证智能电动汽车在极限工况下的行驶稳定性尤为重要。
目前传统汽车常用的稳定性控制系统,如ESP、VSC 与ESC 等,也被广泛应用于智能电动汽车。文献[3]中根据汽车实际横摆角速度和理想横摆角速度的偏差,采用PID 控制得到附加横摆力矩;文献[4]中设计的ESP 系统基于人工鱼群算法和模拟退火算法对PID 控制器的参数进行优化,提升其控制效果;文献[5]~文献[9]中采用MPC 控制器有效处理了带约束的稳定性控制问题;文献[10]中采用滑模变结构保证轨迹跟踪的稳定性;文献[11]和文献[12]中分别采用线性矩阵不等式及模糊控制方法计算附加横摆力矩;文献[13]中基于小波控制提高了车辆在对开路面行驶的稳定性;文献[14]~文献[16]中使用了转矩矢量控制方法对各驱动电机的驱动力矩进行控制,将理想质心侧偏角和横摆角速度限制在一定范围内。以上研究提供了丰富的稳定性控制策略,这些策略均通过调节轮胎纵向力实现。有学者根据纵、横向力综合作用对汽车稳定性的影响,采用DYC 和AFS 集成控制的方法提高智能电动车辆的稳定性。文献[17]中研究了基于H∞的线性二次型调节器,控制主动前轮转向和附加横摆力矩。文献[18]和文献[19]中采用T-S 模糊控制提高车辆的侧向稳定性。文献[20]和文献[21]中采用MPC 协调汽车的主动转向角和纵向力。这类控制方式依赖于集成控制器对系统实时状态的动态评估及对两种子控制器的协调效果,对协调控制的逻辑提出了较高要求。
上述系统对于任何干扰引起被控量的变化,均根据被控量实际值与参考值之间的偏差进行调节,属于反馈控制,这种控制机制在偏差出现后开始作用,存在滞后性,可能导致系统错过最佳的调节时机。针对这一问题,有学者开展了前馈控制研究[22,24]。文献[23]中基于卡尔曼滤波理论设计前馈控制器,减弱干扰对横摆性能的影响。文献[24]中以汽车2 自由度模型和理想横摆角速度为参考,设计反馈控制律,在偏差出现之前对系统进行修正,能有效弥补反馈控制的不足。然而,这些控制策略的制定依赖于当前车辆状态,或只考虑当前坐标下的道路信息,这会在一定程度上造成车辆对前方路径信息的预见性不佳。文献[25]和文献[26]中通过建立预瞄模型引入前方道路曲率,不断获取前方一段距离内预瞄点的曲率来控制车辆。然而,基于预瞄的理论大多用于路径跟踪控制,少有在稳定性控制问题中得以充分应用。
因此,本文以分布式前轮驱动智能电动汽车为研究对象,提出了一种融合预瞄特性的稳定性控制方法,以充分利用感知系统提前掌握前方路况信息的优势,使得稳定性控制策略的制定不仅依赖于车辆姿态,同时受路况信息的指导。本文研究内容主要包括以下部分:(1)在已知未来道路信息的基础上,建立预瞄模型引入前方道路曲率,在此作为稳定性控制的依据;(2)以道路条件和拟人化驾驶为约束,建立弯道车速模型,根据车辆的行驶状态设计前馈控制律,补偿轮胎侧偏刚度变化对稳定性的影响;(3)基于MPC 理论设计反馈控制律,研究预测模型参数和预测时间的自适应优化方法,构建前馈+反馈稳定性控制系统,使其既具有前馈控制及时的优点,又能发挥反馈控制的抗干扰能力和弥补前馈控制误差的作用,提升智能电动汽车稳定性控制的效果。
1 模型建立
1.1 预瞄模型
预瞄模型是预瞄理论的基础。建立的车辆预瞄模型如图1 所示,以车辆质心为运动参考点,将车辆运行前方一定预瞄距离处的点作为预瞄点,该点与道路中心线切线之间的距离为横向偏差,预瞄点处车辆纵向中心线与道路中心线切线之间的夹角为航向角偏差。
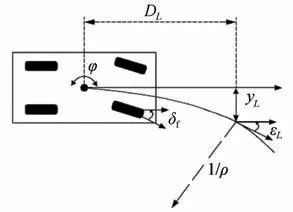
图1 车辆预瞄模型
该模型可表示为
式中:DL为预瞄距离;yL为横向偏差;εL为航向角偏差;u为汽车纵向速度;v为汽车横向速度;φ为汽车横摆角;ρ为待执行路径的曲率。
1.2 稳定性理想状态参考模型
本文在研究汽车稳定性问题时忽略悬架的影响,认为汽车只做平行于水平面的运动。为简化计算,采用2 自由度模型作为稳定性理想状态参考模型,汽车质心侧偏角和横摆角速度[26]为
考虑汽车运动受路面附着条件的限制,理想状态下质心侧偏角和横摆角速度为
式中:m为汽车质量;L为轴距;a、b分别为汽车质心到前、后轴的距离;δf为前轮转角;μ为路面附着系数;K为稳定性因数分别为前、后轮侧偏刚度。
2 基于轮胎侧偏刚度补偿的稳定性前馈控制
2.1 基于预瞄的纵向加速度规划
车辆纵向运动受道路附着条件、道路形状及拟人化驾驶风格的影响,其纵向加速度规划模型如图2所示。

图2 车辆加速度规划模型
根据当前车速和预瞄路段的曲率,可以计算出通过未来一定距离目标路径时的纵向加速度的变化。忽略道路横向坡度的影响,由于地面附着条件的限制,允许通过的最高车速umax应满足:
定义汽车不发生侧滑的最大车速为
式中:系数kv取决于汽车质量和几何参数等,通常取0.6~0.9,本文取0.8;Ay为安全车速裕量,通常选0.7。
汽车通过大曲率路径时,适当地降低车速对保证路径跟踪精度及稳定性尤为重要,驾驶人根据驾驶经验,在通过弯道时通常会减速。为使得智能汽车具有拟人化的行为特征,通过弯道时选择指数车速模型计算目标车速[27]:
式中ζ表示车速对道路曲率变化的敏感度,较小的ζ表示对道路曲率的变化敏感度高,弯道行驶时车速降低较为明显,较大的ζ表示对道路曲率变化的反应较小,弯道行驶倾向于选择较高车速,本文取ζ为0.9。
根据式(6)与式(7),汽车在预瞄点处期望车速的上限为
若当前车速u小于期望车速上限ud,则汽车以当前车速过弯不会发生侧滑,同时满足拟人化驾驶对弯道安全车速的预期,可保持当前车速通过;若当前车速u大于ud,为提高过弯时的稳定性与安全性,汽车须减速行驶。这一过程的汽车纵向加速度可由PID控制计算得出:
式中:e(t)为目标车速与当前车速的偏差,即e(t)=u-ud;kp、ki和kd分别为控制器的比例、积分和微分系数。
2.2 基于轮胎侧偏刚度补偿的前馈控制律设计
当道路曲率改变时,汽车在跟踪目标路径的过程中,车身姿态将发生变化,轮胎的侧偏特性也随之改变。为量化侧偏刚度变化对汽车稳定性的影响并进行稳定性控制补偿,将汽车初始状态的稳态转向模型作为标称模型,此时侧偏刚度大小为轮胎处于线性区域时的侧偏刚度值,定义其为名义侧偏刚度。同时,将道路曲率看作外界对汽车稳定状态的干扰,由干扰引起的侧偏刚度的变化如式(10)所示:
为补偿干扰带来的Δk1与Δk2部分,设计前馈控制律,对汽车稳定性状态进行调节。采用当前轮胎侧偏刚度描述其转向特性,此时汽车的横摆角速度为
汽车前、后轴实际侧偏刚度与前、后轴载荷有关,此处考虑载荷转移对侧偏刚度的影响,在纵向加速度作用下轮胎的有效侧偏刚度[28]为
式中:Fzi为名义垂直载荷为纵向力作用下垂直载荷转移后的值;i=1代表前轴,i=2代表后轴。
名义垂直载荷与纵向力作用下垂直载荷转移后的值为
式中ΔFz为载荷转移量。
根据汽车在预瞄点处横摆角速度和名义稳态横摆角速度的差,通过前馈控制补偿轮胎侧偏刚度的变化,调整车辆姿态,以提高汽车稳定性。前馈控制量采用比例控制得出:
式中KFF为前馈控制比例系数。
3 基于参数自适应的稳定性模型预测反馈控制
3.1 汽车稳定性控制器整体结构
前馈控制能根据预瞄信息在曲率变化时计算控制输入,这一过程相当于开环控制,难以处理系统实际状态与目标值之间的误差,故当汽车在行驶过程中受到侧向风、路面不平等带来的干扰时,无法保证控制精度。因此,需要在前馈控制的基础上加入反馈机制,当状态量实际值与目标值之间存在误差时修正车辆姿态,在提高系统抗扰动性能的同时,有效提高控制精度。
本文设计的前馈+反馈稳定性控制架构如图3所示。其中,前馈控制根据当前轮胎侧偏刚度和名义侧偏刚度之差,采用高增益的PI 控制输出前馈控制附加横摆力矩。反馈控制中参考模型通过采集前轮转角与车速等信息,计算出理想横摆角速度和质心侧偏角,根据实际横摆角速度和质心侧偏角与理想值的偏差,采用MPC 控制器输出相应的反馈控制附加横摆力矩,前馈控制附加横摆力矩和反馈控制附加横摆力矩同时作用于被控车辆,由此提升车辆的稳定性。

图3 前馈+反馈稳定性控制架构
3.2 模型预测控制策略设计
由于模型预测控制不需要得知被控对象的具体结构,且对模型误差具有较强的鲁棒性,故本文采用模型预测控制设计车辆的稳定性反馈控制器。考虑到传统线性时不变模型预测控制难以处理模型参数随时间变化的问题,本文根据汽车对前方路况的预见信息,采用时变侧偏刚度更新预测模型参数,其控制逻辑如图4所示。
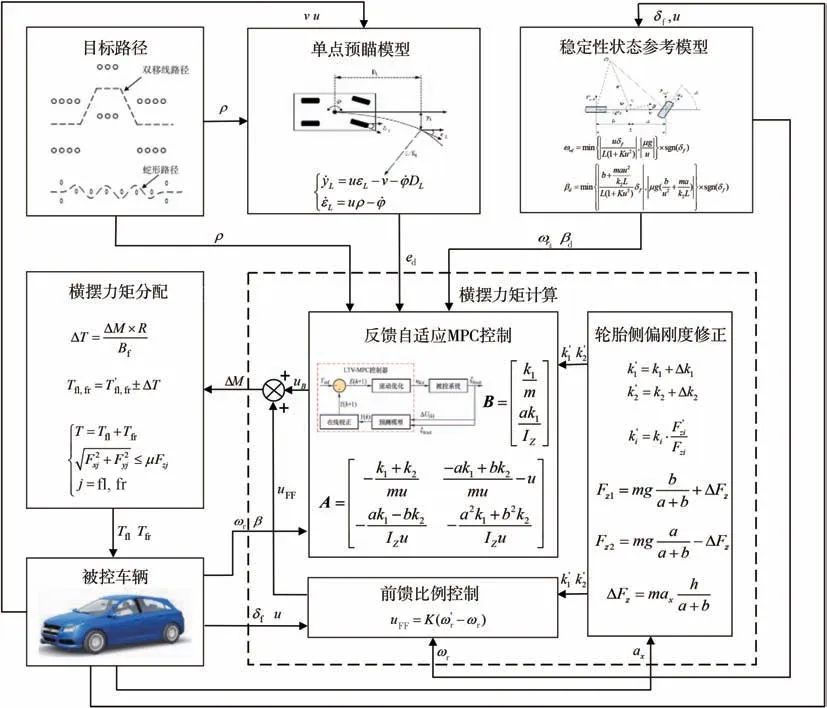
图4 模型预测反馈控制逻辑
以2 自由度车辆状态空间方程作为预测模型,设计跟踪理想质心侧偏角和横摆角速度所需的附加横摆力矩。状态空间方程可描述为是使汽车恢复到理想状态所需的控制量,即反馈附加横摆力矩。
系统的控制输出为
MPC基于状态采样,对系统进行离散处理,得离散形式的状态方程为
式中:k表示当前时刻,k时刻的状态值为x(k),以此作为预测智能电动汽车未来动态的起点;x(k+1)为k+1 时刻的状态;y(k)为系统在k时刻的输出;A1=I+AT;B1=BT;C1=C;T为控制步长;I为单位矩阵。
将状态变量与控制变量相结合,得到扩维的状态变量:
令预测时域为Np,控制时域为Nc,根据预测模型对系统未来时刻状态的预测如下:
系统未来的状态可由以下预测方程得出:
预测输出为
进行稳定性控制时,不仅要跟踪理想质心侧偏角和横摆角速度,还须限制控制成本和约束的松弛程度,因此,将控制目标定义为控制变量和系统状态跟踪误差的加权求和。当系统处于k时刻,模型预测控制的优化目标函数可写为如式(25)所示的二次型。
考虑到执行机构的约束及对控制量平稳程度的要求,对控制量、控制增量及输出量做出限制,同时为确保优化问题有可行解,加入松弛因子对约束进行软化:
当车辆状态发生变化时,采用基于载荷转移的修正侧偏刚度实时更新预测模型中的k′1与k′2(式(16)),使模型参数随车辆转向特性的变化而进行调整,得考虑轮胎时变侧偏刚度的自适应参数MPC 控制器。
采用二次规划算法,计算每个控制周期的控制序列,其中第一个元素即为反馈控制的输出。结合式(15)给出的前馈控制输出,得最终附加横摆力矩ΔM。
为了通过控制驱动轮转矩,实现此目标需求附加横摆力矩,左、右驱动轮力矩分别改变ΔT:
式中:ΔM为附加横摆力矩;R为前轮半径;Bf为前轮距。
对于分布式前轮驱动汽车,此时左、右驱动轮需求转矩为
式中:Tfl,fr和T′fl,fr分别为附加横摆力矩分配前和分配后左、右前轮的驱动转矩;下标fl代表左前轮,fr代表右前轮。
分配的转矩须满足车辆行驶需求转矩和路面附着约束,即
式中:T为需求转矩;Fxj和Fyj分别为前轮纵向力和侧向力;Fzj为前轴驱动轮垂直载荷。
3.3 预测时间自适应优化
在模型预测控制中,控制效果依赖于预测时间的选择。采用固定的预测时间,难以在不同工况下取得最优的控制效果,本文根据当前的车-路信息,对MPC的预测时间进行优化。
MPC控制的预测时间t为
式中:Np为预测时域;Tp为预测步长。
若将目标轨迹表示为yr=f(xr),在预瞄距离内选择Np个采样点xr,j,其中j=1,2,…,Np。以道路因子lp评价预瞄距离内轨迹的几何特性,定义lp如下:
式中:ρ(xr,j)为参考采样轨迹点xr,j处的曲率;Np的初值取15。
由此可知,预瞄轨迹的平均曲率越大,lp也越大。在汽车行驶过程中,Np随道路几何形状的变化而变化,定义Np为lp的函数,其函数关系可用指数函数表示[29]:
式中:p=2.5;q=22.5;r=-14.64。由于预测时域为整数,采用round(·)将计算结果圆整为整数。
因此,当前方道路曲率越小,预测时域则越大,须增加汽车的稳定性;反之,当前方道路曲率越大,则选取较小的预测时域保证轨迹跟踪精度。
预测步长Tp的选择依赖于当前车速,当车速较大时,应适当增加预测步长,以提前预知前方道路信息,考虑更多的未来轨迹变化情况,从而提高轨迹跟踪的平稳性。然而,预测步长过大,在预测时域内的预测距离随之增大,导致对目标路径的跟踪能力下降,从而引发较大的跟踪偏差。因此,当侧向偏差较大时,须减小预测步长,以保证汽车跟踪轨迹的精度。针对这一控制需求,采用BP神经网络优化预测步长[30]。
以车速和横向偏差为输入,以预测步长为输出构建神经网络,如图5 所示。经试凑法确定本文采用单隐含层的3 层网络结构,输入层神经元数量为2,分别代表车速u和跟踪偏差ed,隐含层神经元数量为4,输出层为单神经元,代表预测步长。
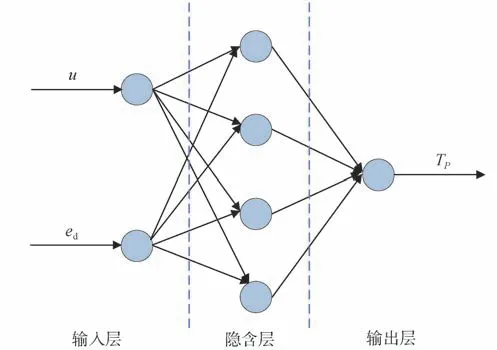
图5 BP神经网络结构图
通过大量仿真实验,建立车速、偏差与预测步长之间的映射关系,以此对神经网络进行训练。
网络的输入层为
网络隐含层的输入、输出为
式中ω为加权系数。
网络输出层的输入、输出为
隐层神经元的激活函数选用Sigmoid函数:
输出层输出节点为预测步长,输出层神经元的激活函数取线性函数。
采用梯度下降法修正权系数:
式中:η为学习率,本文取0.1;E(n)为代价函数,
4 仿真验证与分析
为验证本文设计的控制策略的有效性,基于MATLAB/Simulink 和CarSim 联合仿真环境进行试验。联合仿真逻辑框图如图6 所示,整车参数见表 1。
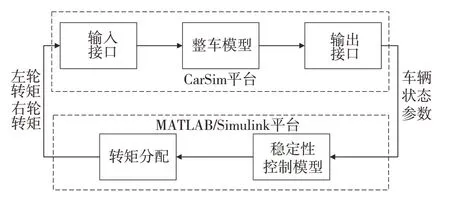
图6 联合仿真逻辑框图
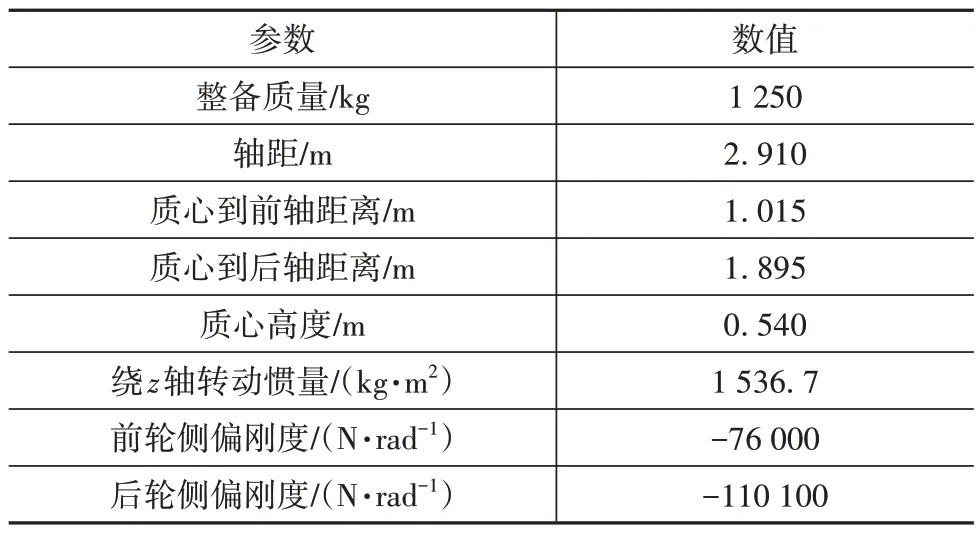
表1 整车参数表
选择双移线轨迹,设置车速90 km/h、路面附着系数为0.6 和车速120 km/h、路面附着系数为0.85的两种工况,在无稳定性控制、仅有MPC 反馈控制、前馈+固定参数MPC 反馈控制及前馈+自适应参数MPC反馈控制4种方式下进行仿真,轨迹曲率如图7所示,仿真结果如图8和图9所示。
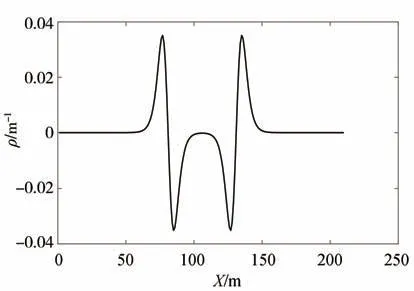
图7 双移线轨迹曲率
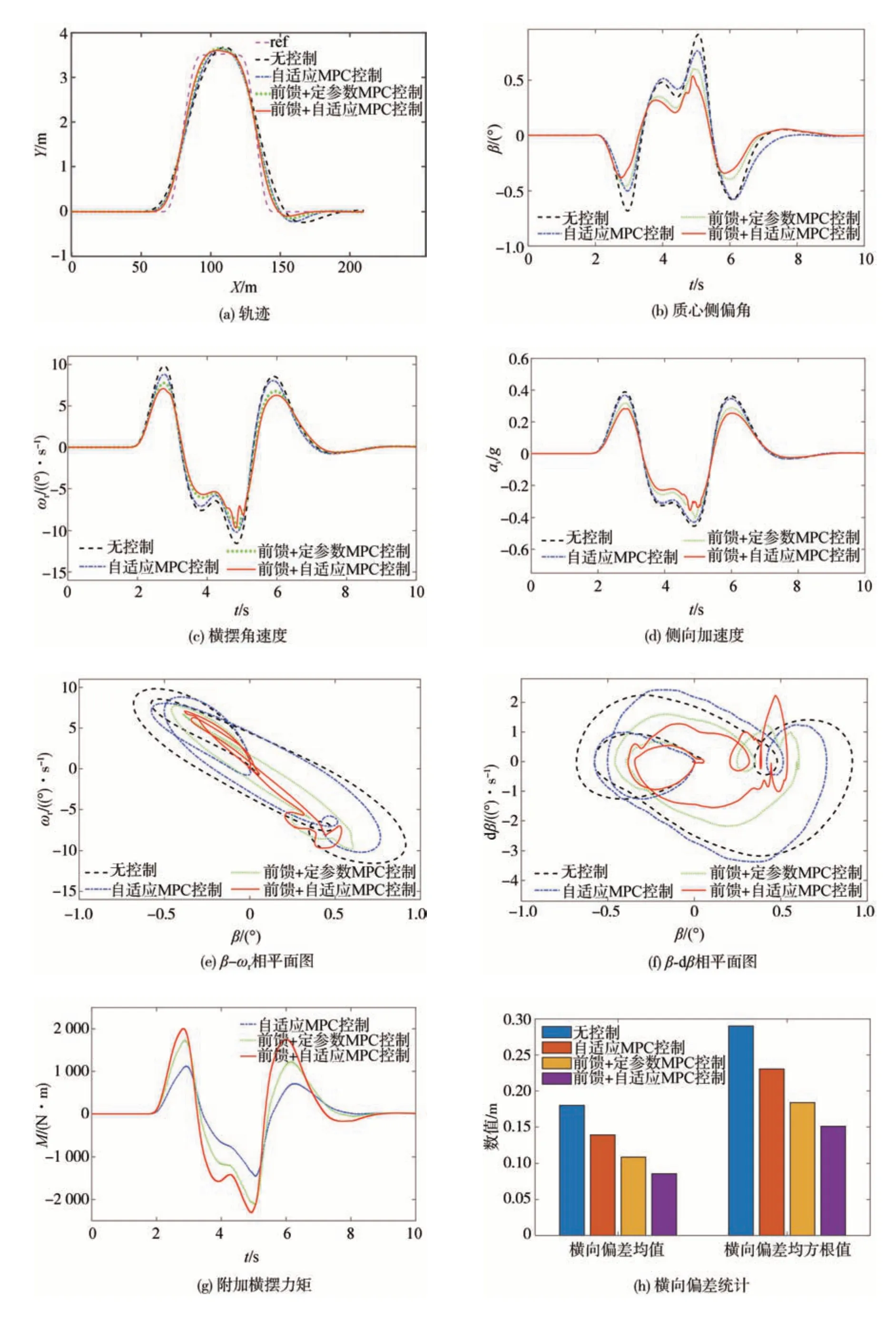
图8 双移线工况:车速90 km/h,路面附着系数0.6
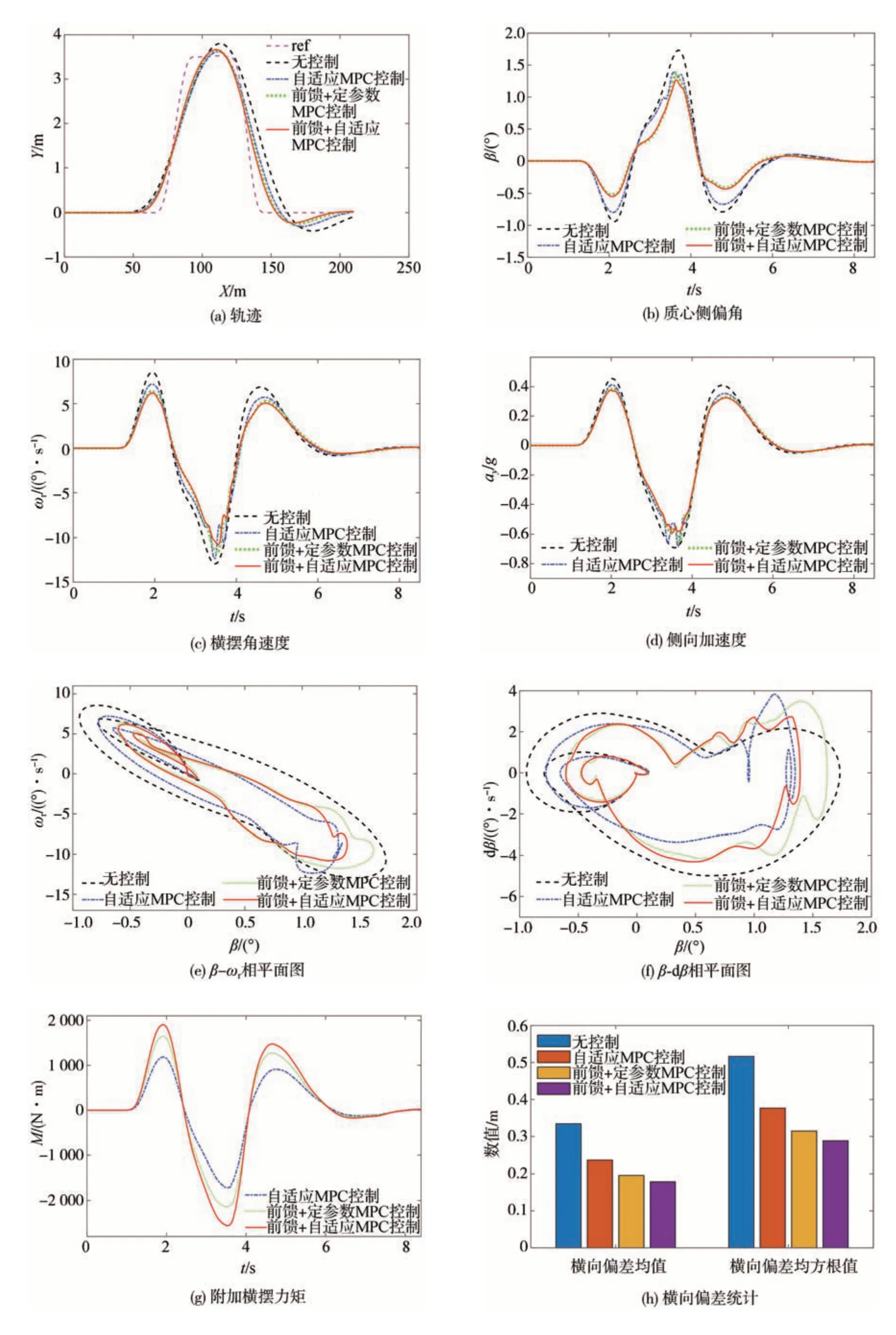
图9 双移线工况:车速120 km/h,路面附着系数0.85
从图7 可以看出,理想轨迹的曲率在两次换道处出现较大幅度波动,最大曲率约为0.035 m-1。由图8 和图9 可知,在4 种控制方式下车辆均能完成对期望轨迹的跟踪,但无稳定性控制时,实际轨迹与参考轨迹的偏差较大,而在前馈+自适应参数MPC 控制下,实际轨迹与参考轨迹的偏差最小,这种情形在两次换道处尤为明显。从质心侧偏角-横摆角速度、质心侧偏角-质心侧偏角速度相平面图可以看出,4 种控制方式下曲线均能回到原点,然而曲线范围不同,前馈+自适应参数MPC 控制相较于无控制作用下曲线范围减小。由附加横摆力矩图可知,3 种控制方式下的附加横摆力矩变化趋势相同,与质心侧偏角及横摆角速度偏差的变化趋势也基本一致。从横向偏差统计图可以看出,无控制时车辆横向误差较大,稳定性控制能纠正车辆姿态,有助于提高汽车对理想轨迹的跟踪精度,其中采用本文提出的控制策略时其跟踪偏差均值与均方根均最小。
车速为90 km/h、路面附着系数为0.6 时,在约4.8 s 处汽车质心侧偏角和横摆角速度出现最大值。无稳定性控制、MPC 控制、前馈+定参数MPC 控制与前馈+自适应参数MPC控制4种方式下,质心侧偏角的变化范围分别为-0.68°~0.92°、-0.57°~0.76°、-0.46°~0.60°、-0.38°~0.54°,横摆角速度范围分别为-11.75~9.830、-10.33~8.81、-9.84~7.73、-9.64~7.03(°)/s,侧向加速度范围分别为-0.45g~0.39g、-0.43g~0.36g、-0.39g~0.32g、-0.35g~0.28g;在对理想轨迹的跟踪精度方面,横向偏差均值分别为0.18、0.14、0.11 和0.09 m,均方根分别为0.29、0.23、0.18 和0.15 m。相较于无控制、MPC 控制和前馈+定参数MPC控制,前馈+自适应参数MPC控制下的质心侧偏角峰值分别减小了41.3%、28.9%和10.0%,横摆角速度峰值分别减小了18.0%、6.7%和2.0%,侧向加速度峰值分别减小了22.2%、18.6%和10.3%;横向偏差均值分别减小了50.0%、35.7%和18.2%,偏差均方根分别减小了48.2%、34.8%和16.7%。
车速为120 km/h、路面附着系数为0.85 时,本文提出的控制策略同样能将质心侧偏角、横摆角速度与侧向加速度的变化控制在一定范围内。在无稳定性控制、MPC 控制、前馈+定参数MPC 控制与前馈+自适应参数MPC控制4种方式下,质心侧偏角范围分别为-0.94°~1.73°、-0.80°~1.38°、-0.52°~1.37°、-0.53°~1.26°,横摆角速度范围分别为-12.94~8.53、-12.34~7.20、-11.76~6.42、-10.75~6.18(°)/s,侧向加速度范围分别为-0.69g~0.43g、-0.68g~0.41g、-0.66g~0.38g、-0.58g~0.37g;横向偏差均值分别为0.33、0.24、0.19 和0.17 m,均方根分别为0.51、0.37、0.31 和0.28 m。相较于无控制、MPC 控制和前馈+定参数MPC 控制,前馈+自适应参数MPC 控制下的质心侧偏角峰值分别减小了27.2%、8.7%和8.0%,横摆角速度峰值分别减小了16.9%、12.9%和8.6%,侧向加速度峰值分别减小了15.9%、14.7%和12.1%;横向偏差均值分别减小了48.4%,29.2%和10.5%,偏差均方根分别减小了45.1%,24.3%和9.7%。双移线工况下不同控制策略的稳定性仿真结果对比如表 2所示。
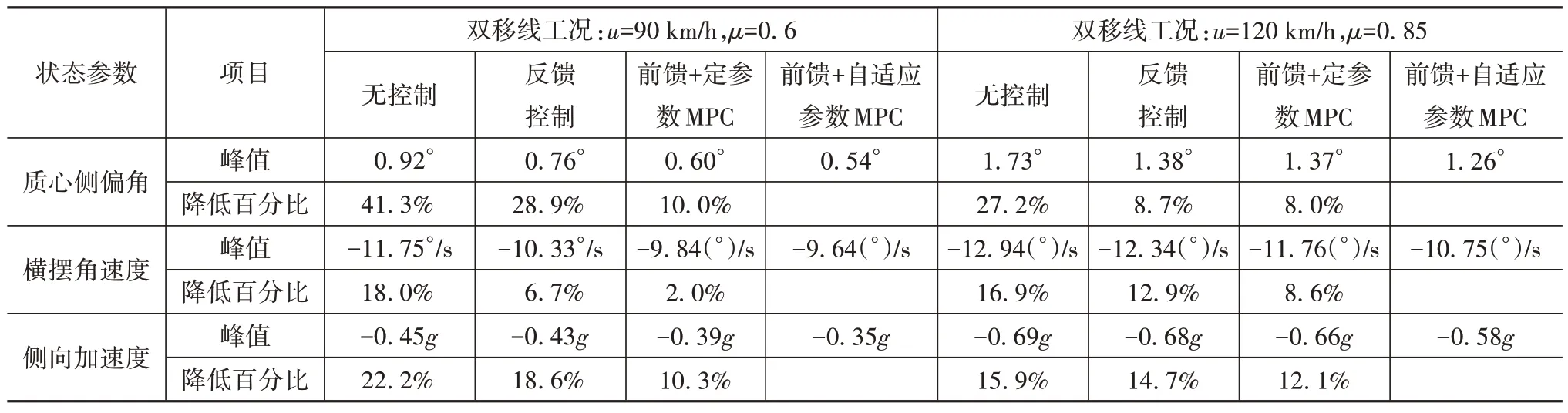
表2 双移线工况下不同控制策略稳定性仿真结果对比
选择蛇行工况,设置不同车速与路面附着条件,在4种控制方式下进行仿真,轨迹曲率如图10所示,仿真结果如图11和图12所示。

图10 蛇行轨迹曲率
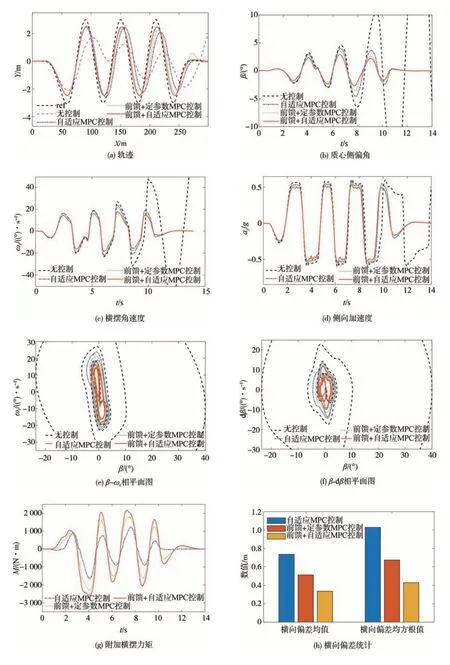
图11 蛇行工况:车速90 km/h,路面附着系数0.6
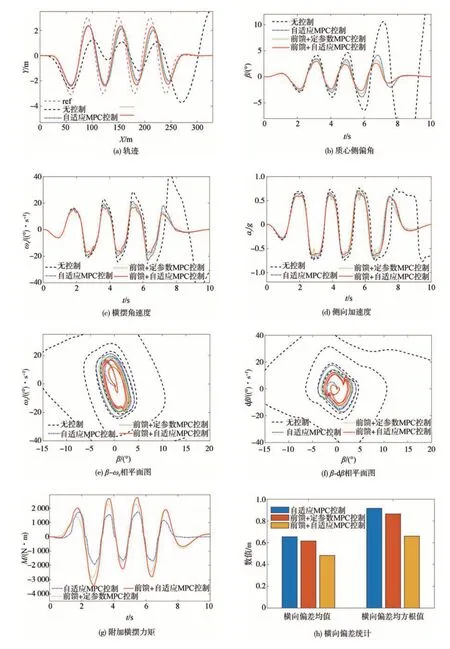
图12 蛇行工况:车速120 km/h,路面附着系数0.85
由此可以看出,蛇行轨迹的曲率呈周期性波动,曲率最大处所对应的汽车质心侧偏角、横摆角速度和侧向加速度也较大。无稳定性控制时,两种蛇行工况下汽车行驶轨迹逐渐发散,无法完成对期望轨迹的跟踪。在纵向距离为260 m 后,期望轨迹为直线,理想质心侧偏角与横摆角速度均为零,其实际值却依然很大且存在继续增加的趋势,车辆稳定性无法得到保证。而稳定性控制策略可使汽车沿期望轨迹行驶,其中本文所提控制策略下的轨迹与理想轨迹偏差最小,同时将质心侧偏角、横摆角速度与侧向加速度控制在一定范围。根据相平面图可知,无稳定性控制时,质心侧偏角-质心侧偏角速度及质心侧偏角-横摆角速度相平面曲线均无法回到原点,而有稳定性控制介入时,其相平面曲线可回到原点,且在本文所提控制策略下,相平面曲线的作用范围最小。与双移线工况类似,3 种稳定性控制方式下的附加横摆力矩在质心侧偏角和横摆角速度跟踪偏差较大处差异相对明显,但整体变化趋势一致。由横向误差统计图可知,稳定性控制策略也有助于提高轨迹跟踪精度。
车速为90 km/h 时,在MPC 控制、前馈+定参数MPC控制与前馈+自适应参数MPC控制3种方式下,质心侧偏角变化范围分别为-4.57°~3.90°、-3.51°~3.50°、-2.92°~2.92°,横摆角速度范围分别为-22.23~23.66、-21.04~21.19、-18.48~18.50(°)/s,侧向 加速度范 围分别为-0.57g~0.58g、-0.54g~0.55g、-0.52g~0.53g,相较于前两种控制方式,在本文提出的控制策略下车辆的质心侧偏角峰值减小了49.8%和34.8%,横摆角速度峰值减小了21.8%和12.7%、侧向加速度峰值减小了8.6%和3.6%。在轨迹跟踪精度方面,无控制时车辆已无法跟踪轨迹,3 种稳定性控制策略下,横向偏差均值分别为0.73、0.51 和0.33 m,均方根分别为1.02、0.67 和0.42 m,相较于前两种控制方式,本文提出的控制策略其偏差均值分别减小了54.8%和35.3%,均方根分别减小了58.8%和37.3%。
当车速高达120 km/h 时,MPC 控制、前馈+定参数MPC控制与前馈+自适应参数MPC控制下的质心侧偏角范围分别为-4.13°~4.13°、-3.21°~3.15°、-2.61°~2.60°,横摆角速度范围分别为-22.95~20.95、-19.69~19.67、-17.24~17.06(°)/s,侧向加速度范围分别为-0.70g~0.70g、-0.69g~0.68g、-0.65g~0.65g,横向偏差均值分别为0.65、0.61 和0.48 m,偏差的均方根分别为0.91、0.86 和0.66 m。相较于MPC 控制和前馈+定参数MPC 控制,本文提出的控制策略的车辆质心侧偏角峰值减小了36.6%和18.6%,横摆角速度峰值减小了17.7%和12.4%、侧向加速度峰值减小了7.1%和5.8%,横向偏差均值减小了26.1%和21.3%,均方值减小了27.5%和23.2%。蛇行工况下不同控制策略的稳定性仿真结果对比如表 3所示。
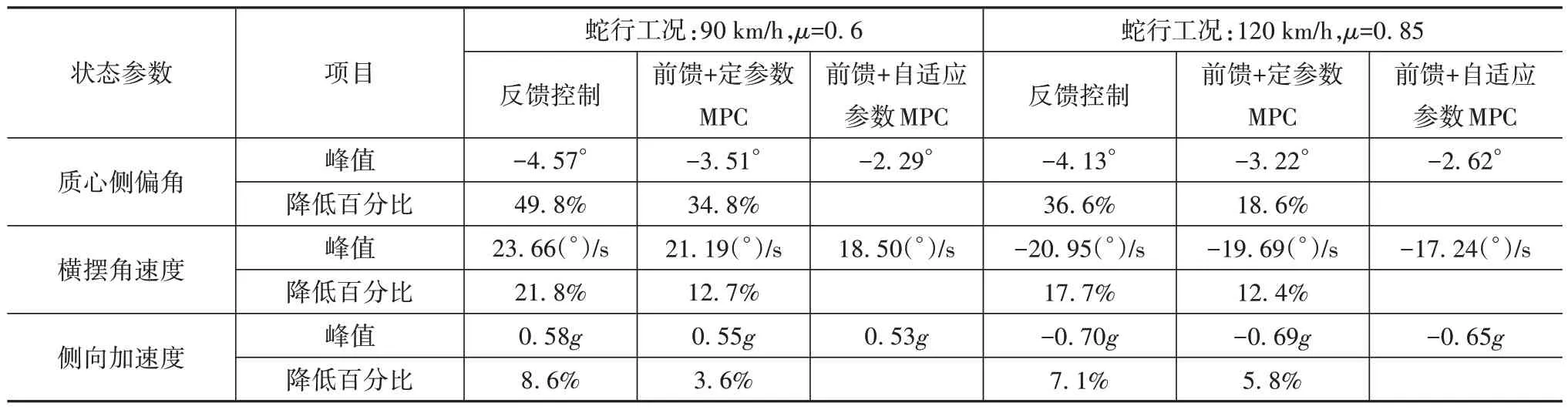
表3 蛇行工况下不同控制策略的稳定性仿真结果对比
综上,本文根据车辆对前方路况的预瞄信息,提出的前馈+反馈稳定性控制策略可充分发挥前馈控制作用及时、滞后性小以及反馈控制能抵抗多种干扰和消除偏差的优点,取得了良好的控制效果。
5 结论
(1)研究了基于预瞄信息的前馈+反馈稳定性控制系统。其中,前馈控制补偿了侧偏刚度变化对模型带来的影响,弥补了反馈控制作用不及时的缺点;模型预测反馈控制消除系统误差,提高了控制的精确性。
(2)基于预瞄信息对模型预测控制的预测模型参数和预测时间进行自适应优化,使其能在不同工况下取得良好的控制效果。
本文所设计的控制系统未考虑汽车侧倾带来的影响,未来可基于更精确的模型开展研究,进一步提升控制精度和效果。
