双环多杆天线展开机构运动学与动力学分析
2023-05-28韩媛媛许允斗姚建涛赵永生
韩 博 高 超 韩媛媛 许允斗 姚建涛 赵永生
(1.燕山大学机械工程学院, 秦皇岛 066004; 2.衡水学院数学与计算机科学系, 衡水 053000)
0 引言
遥感卫星技术以及遥感地面应用技术已经广泛地应用于农业生产监测,包括作物面积与空间分布、生长情况、病虫害、产量预报预测等[1]。空间可展开天线作为遥感卫星的一部分,是一种为了更好地满足航天器结构大型化发展趋势而产生的具有折叠与展开功能的新型航天装备[2-3]。其在发射过程中处于折叠收拢状态,进入轨道后按控制指令逐渐展开并锁定,具有支撑定位、收集能量、传递信号等作用[4-6]。环形可展开天线具有收拢率高、质量轻、展开面积大等特点,是可展开天线中应用较多的一种结构形式[7-8]。
环形可展开天线整体呈环形,由若干个相同的并联机构单元组成,单元与单元之间通过运动副连接,其中双环可展开天线相较于单环可展开天线结构更为复杂,展开过程中涉及到复杂的运动学与动力学问题[9]。
由于受到实验条件等因素的限制,对环形可展开天线进行运动学和动力学建模与仿真,是了解和改善其运动学与动力学特性最为有效的手段[10]。为此相关学者做了大量研究,文献[11]成功研制了口径为6 m的双环环形可展开天线,并对其运动学与动力学进行了分析;文献[12]利用闭环矢量法建立了并联机构的运动学模型,基于拉格朗日乘子法建立并联机构的动力学模型,并验证了动力学建模的正确性;文献[13-17]对环形可展开天线进行了深入的研究,并基于广义逆矩阵方法分析了双环可展开天线的运动过程,验证了有限元法分析环形可展开天线动力学的正确性;文献[18]提出一种四自由度高速并联机器人机构,并基于虚功原理建立了机构的动力学方程,通过模型仿真结果验证了动力学模型的正确性;文献[19]对大型环形可展开天线展开过程进行了运动学分析,并提出了一种星载环形天线重力补偿方法;文献[20]对Tripod并联机器人进行了运动学建模与分析,通过ADAMS和Matlab仿真软件对运动学模型进行了验证,通过仿真结果验证了运动学模型的正确性;文献[21-22]对环形可展开天线展开后的结构应力进行了分析,利用有限元软件验证了分析的正确性;文献[23]针对一种四自由度混联天线机构进行了静力学及运动特性仿真与设计;文献[24]利用坐标变换法构建了仿生移动机器人的运动学模型,利用几何建模和数值求解方法进行验证与分析证明,上述研究虽然对可展开机构的运动学与动力学进行了建模与分析,然而使用的建模方法却各不相同,并没有一种程式化的适用于多杆可展开天线运动学与动力学建模与分析的方法。目前空间可展开天线运动学与动力学建模方法有相对坐标法、矢量力学法、自然坐标法、螺旋理论、拉格朗日法和牛顿-欧拉法等。其中文献[25-26]基于螺旋理论和牛顿-欧拉法分析了双层环形桁架可展开天线机构的运动学与动力学特性,通过理论计算与模拟仿真验证了理论模型的正确性,为分析双环可展开天线机构提供了新方法,具有重要的意义。
本文提出一种双环多杆天线展开机构,首先对其构型特征进行分析以及整体机构进行单元分解,然后基于螺旋理论分析双环多杆天线展开机构的速度与加速度,通过坐标转换求导法得到其速度雅可比矩阵,并基于拉格朗日方程建立双环多杆天线展开机构展开过程的动力学方程,最后通过数值计算与模拟仿真来验证理论推导的正确性,并对双环多杆天线展开机构展开过程中的运动学与动力学特性进行分析。
1 双环多杆天线展开机构构型分析
图1为双环多杆天线展开机构,主要由内层环形桁架和外层环形桁架组成,内层环形桁架与外层环形桁架之间通过剪刀式单元连接,双环多杆天线展开机构为双层环形机构,内层环形桁架和外层环形桁架同心设置,机构中各个构件之间均通过转动副连接。
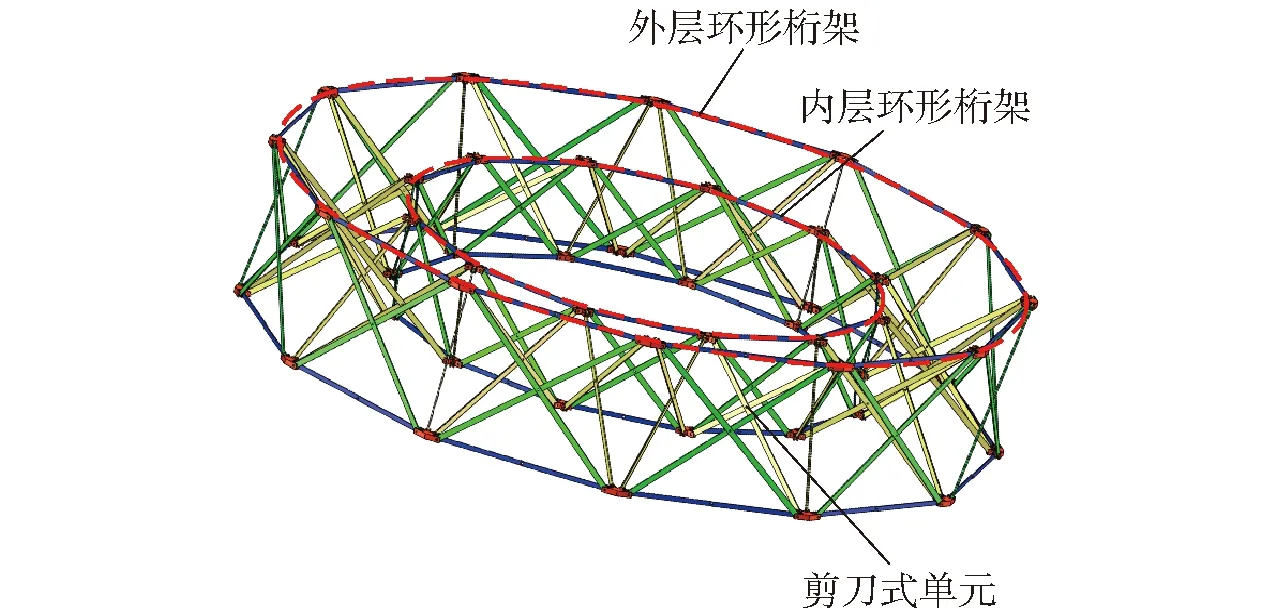
图1 双环多杆天线展开机构
通过对双环多杆天线展开机构的结构特征进行分析,可以将其分解为若干个结构相同的单元机构,如图2所示,相邻单元机构之间共用2个外环节点、2个内环节点和1组剪刀式单元。

图2 双环多杆天线展开机构结构分解
对单元机构进行分解,可再分为如图3~5所示的不同类型剪刀式单元与构件。

图3 2种不同的连接杆单元
图3为2种不同的连接杆单元,内连接杆单元由2根内连接杆通过转动副连接组成,每根内连接杆长度为l1,外连接杆单元由2根长度相等的外连接杆组成,每根外连接杆的长度为L1,2根外连接杆之间通过转动副连接。由图3可知,可将内连接杆单元与外连接杆单元看作是3R平面机构(R表示转动副),内外连接杆单元将可展开天线机构中相邻的2个节点连接起来,增加了双环多杆天线展开机构的刚度,可以提高展开过程中的稳定性。
图4为3种不同类型的剪刀式单元,对于3种剪刀式单元可以看作是5R平面机构。内剪刀式单元位于内层环形桁架上,由2个内长杆通过转动副连接组成,每根内长杆的长度均为l,内剪刀式单元通过转动副与内层节点连接。剪刀式单元位于内层环形桁架与外层环形桁架之间,将内层环桁架与外层环桁架连接起来,一个剪刀式单元由2个中间杆组成,2个中间杆之间通过中心转动副连接,2根中间杆的长度为(l+L)/2。外剪刀式单元由2个外长杆转动副连接组成,外长杆的长度为L,外剪刀式单元位于外层环形桁架上通过转动副与外节点连接,5R平面机构与3R平面机构在单元展开平面内提供相同的约束,内外节点受到重复约束限制了其自身的运动,因此组合后的单元机构为过约束机构,拓扑结构更为复杂。过约束机构的存在不会影响可展开天线机构的展开特性,但却提高了可展开天线机构运动过程的稳定性和可展开天线机构的刚度,因此有必要探究其运动学与动力学特性。
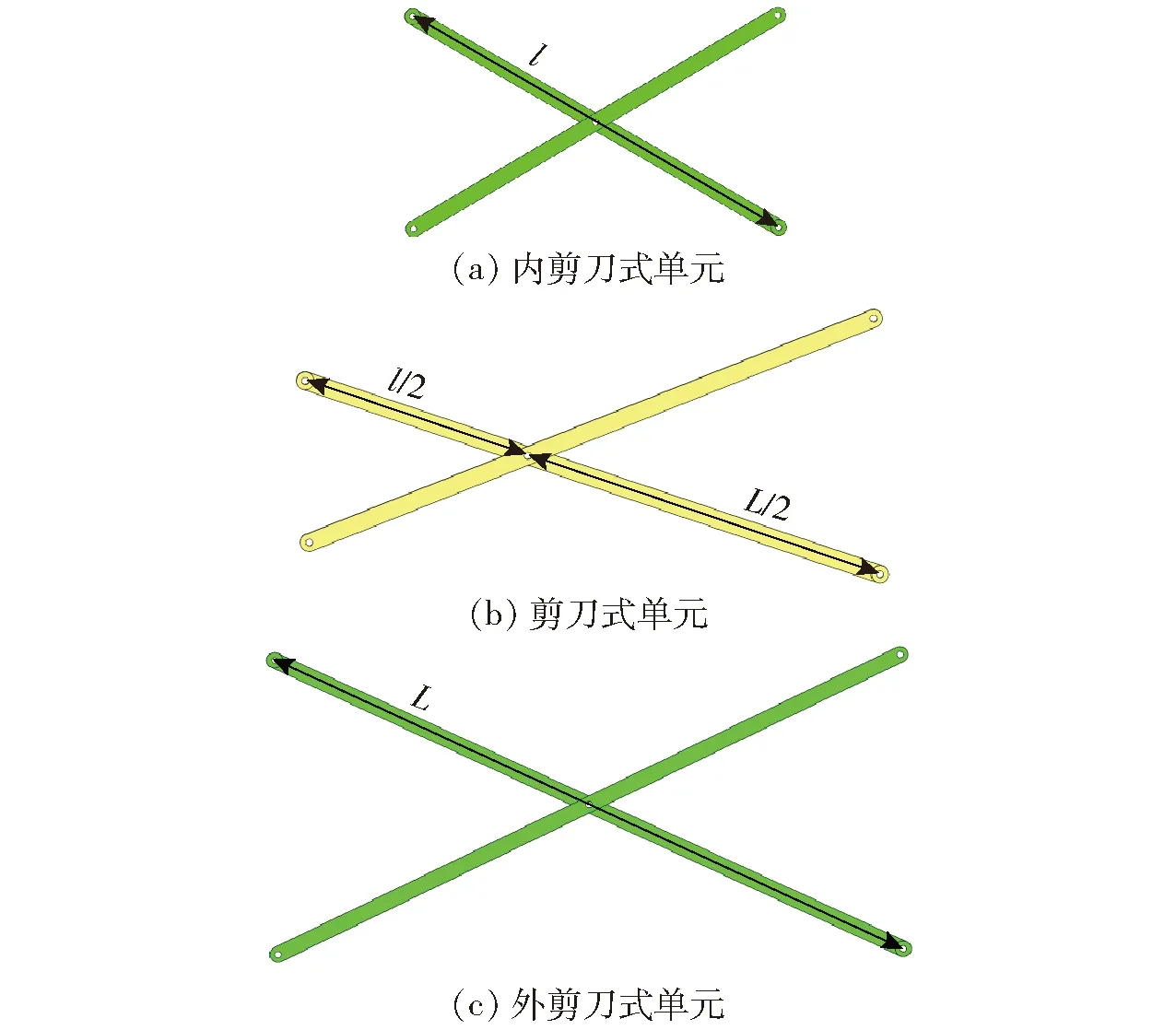
图4 3种不同的剪刀式单元
图5为内环节点示意图,图5内环节点上的转动副轴线与内环节点中心点之间的距离为b,内环节点转动副轴线到内环节点最外侧距离为b1,内环节点作为一个连接节点将2个内连接杆单元连接起来同时与内剪刀式单元相连接,是组成双环多杆天线展开机构的重要构件。
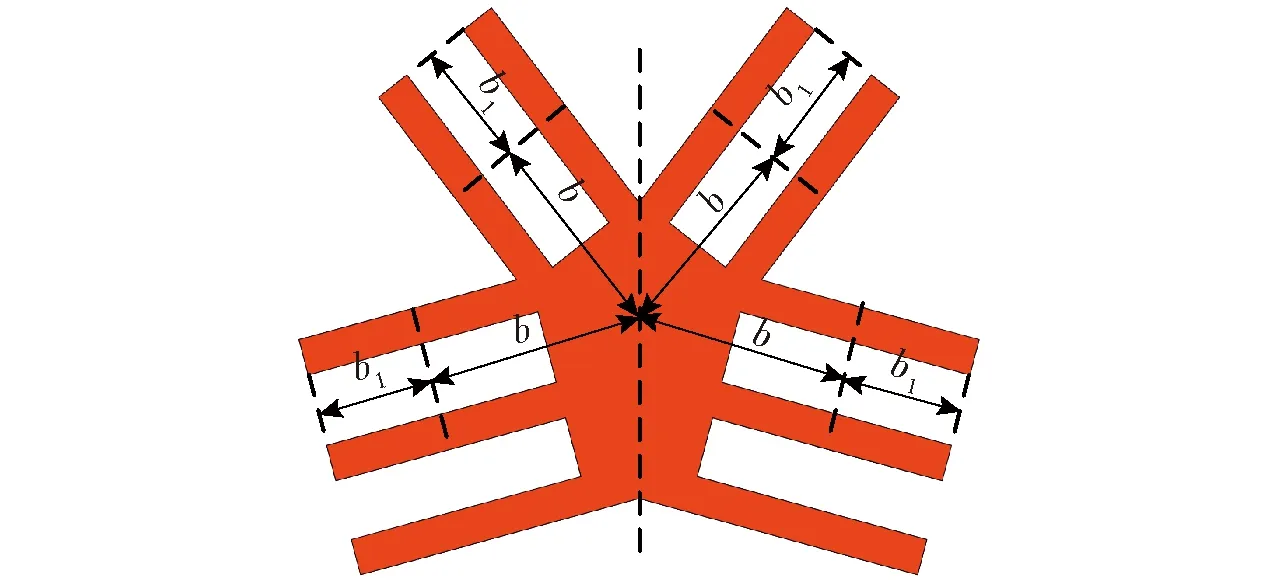
图5 内环节点俯视图
图6为组成单元机构的外环节点示意图,图6中的外环节点中共有2个参数,n为外环节点中心点到转动副轴线的距离,n1为转动副轴线到外环节点最外侧的距离,外环节点将2个外连接杆单元连接起来,同时与外剪刀式单元通过转动副连接。
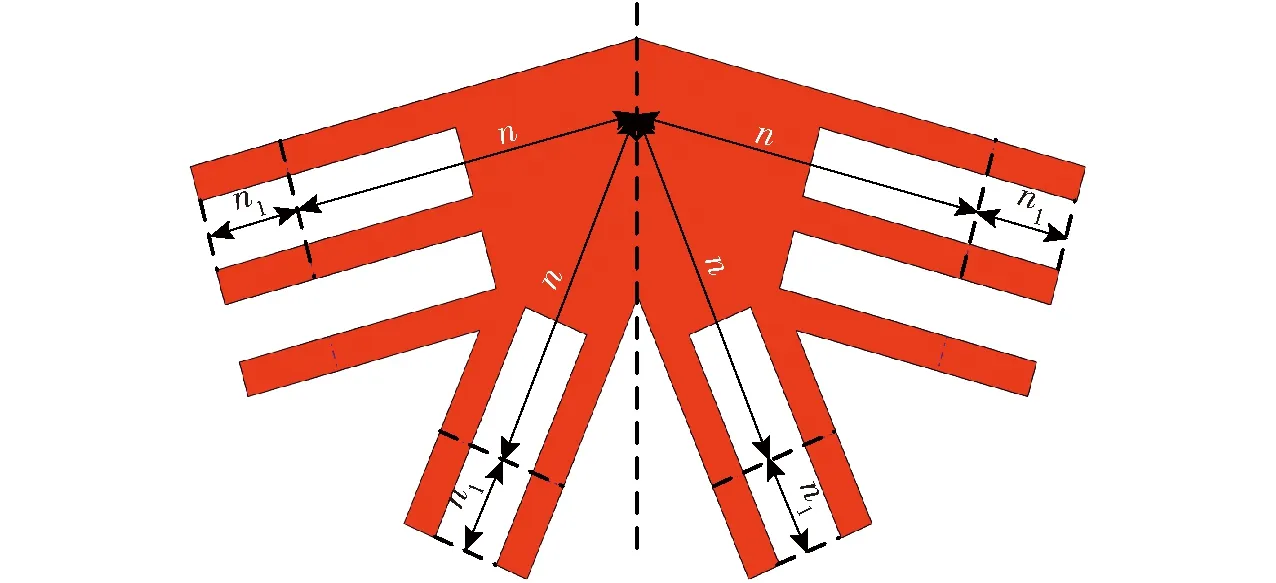
图6 外环节点俯视图
由文献[27]可知,图3~6中所示构件的尺寸参数均满足
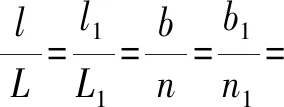
(1)
式中N——可展开天线机构中单元机构的数目
由式(1)可知,随着组成双环多杆天线展开机构的单元机构数目的增加,内层构件与外层构件的尺寸参数比例逐渐增大,但比例不会超过1,即内层环形桁架的尺寸不会超过外层环形桁架的尺寸。
2 双环多杆天线展开机构速度分析
2.1 单元机构中构件速度分析
由第1节分析可知双环多杆天线展开机构由若干个结构相同的单元机构组成,为了便于对单元机构进行速度分析,将其划分为一个封闭单元机构和一个开环单元机构,图7为单元机构分解图,在封闭单元机构的外环节点外接圆圆心处建立空间笛卡尔坐标系,坐标系X轴与节点A中心点和节点B中心点连线重合,Z轴与节点A中心点和节点D中心点连线重合,Y轴的方向由右手法则确定,为了便于建立封闭单元机构和开环单元机构的螺旋约束图,对单元机构中各个构件用字母进行表示。
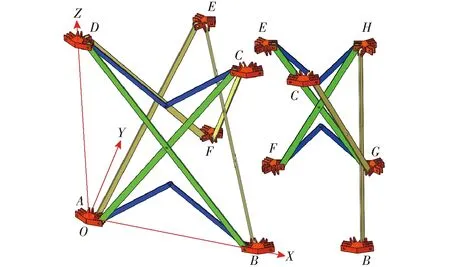
图7 单元机构分解图
封闭单元机构螺旋约束图如图8所示,图中AC表示连接构件A与C之间的外长杆,AB1和AB2表示连接构件A与B之间的2个外连接杆,$i则表示连接2个构件的转动副,利用带箭头的直线来表示运动副,其中箭头方向用于确定动构件与定构件。
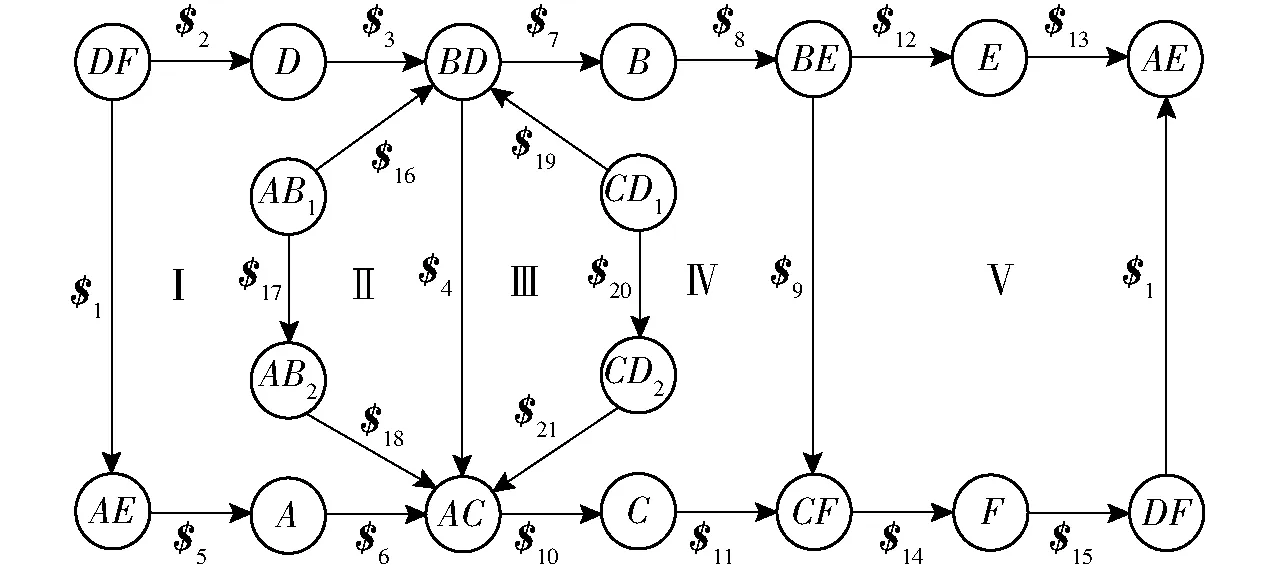
图8 封闭单元机构螺旋约束图
根据图8封闭单元机构的螺旋约束图可得封闭单元机构的约束方程组为
(2)
式中O——6×1维零矢量
ωi——转动副i角速度
开环单元机构的螺旋约束图如图9所示。
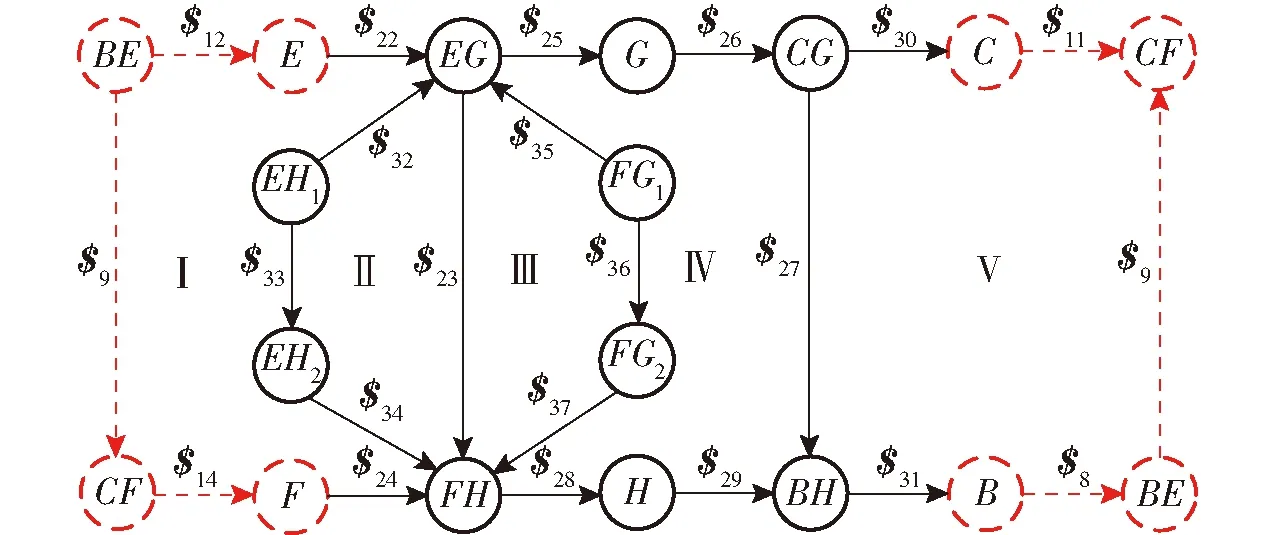
图9 开环单元机构螺旋约束图
根据图9建立开环单元机构约束方程,可以得到开环单元机构的螺旋约束方程组为
(3)
联立式(2)、(3),可得单元机构的螺旋约束方程组为
(4)
由文献[27]可知,整个双环多杆天线展开机构以及组成双环多杆天线展开机构的若干个单元机构均为单自由度机构,因此只需要给定一个输入就可以使展开机构具有确定的运动,当在单元机构中指定位置添加一个驱动时,例如ω1,通过单元机构的约束方程组可以求解出各个构件的角速度,进而由单元机构中封闭单元机构与开环单元机构之间的关系通过螺旋运算可计算出单元机构中各个构件的螺旋速度。
在图8所示的封闭单元机构的螺旋约束图中组成闭环Ⅰ的各个构件速度为
(5)
式中VA、VAC、VAE、VDF、VD、VBD——构件A、AC、AE、DF、D、BD螺旋速度
在图8所示的螺旋约束图闭环Ⅱ中,构件BD、AC的螺旋速度已经通过式(5)求出,因此闭环Ⅱ中其它构件的螺旋速度可以根据已求得构件的螺旋速度计算得到,闭环Ⅱ中其他构件的螺旋速度为
(6)
式中VAB1、VAB2——构件AB1和AB2的螺旋速度
同理根据闭环Ⅰ、Ⅱ求解过程可以依次求出图8中闭环Ⅲ、Ⅳ、Ⅴ中各个构件的螺旋速度,再根据封闭单元机构与开环单元机构之间的几何关系便可求解出开环单元机构中闭环Ⅰ~Ⅴ中各个构件的螺旋速度。
根据速度螺旋的物理意义可知,构件i角速度为
ωi=φ(Vi)
(7)
式中φ(·)——提取速度螺旋前3项
速度螺旋中包含构件角速度和线速度,其中前3项为构件角速度,后3项为构件上与原点重合点的线速度,则构件i质心处线速度为
vi=Φ(Vi)+iri
(8)
式中Φ(·)——提取速度螺旋后3项
ri——坐标原点到构件质心的位移矢量
2.2 相邻单元机构中构件速度分析
双环多杆天线展开机构呈环形,由若干个相同的单元机构组成,单元机构之间通过共用内外节点相互连接,由2.1节分析可知,若各个单元机构在相同的位置建立单元坐标系,则各个单元相同位置处的构件的运动特性必然相同。

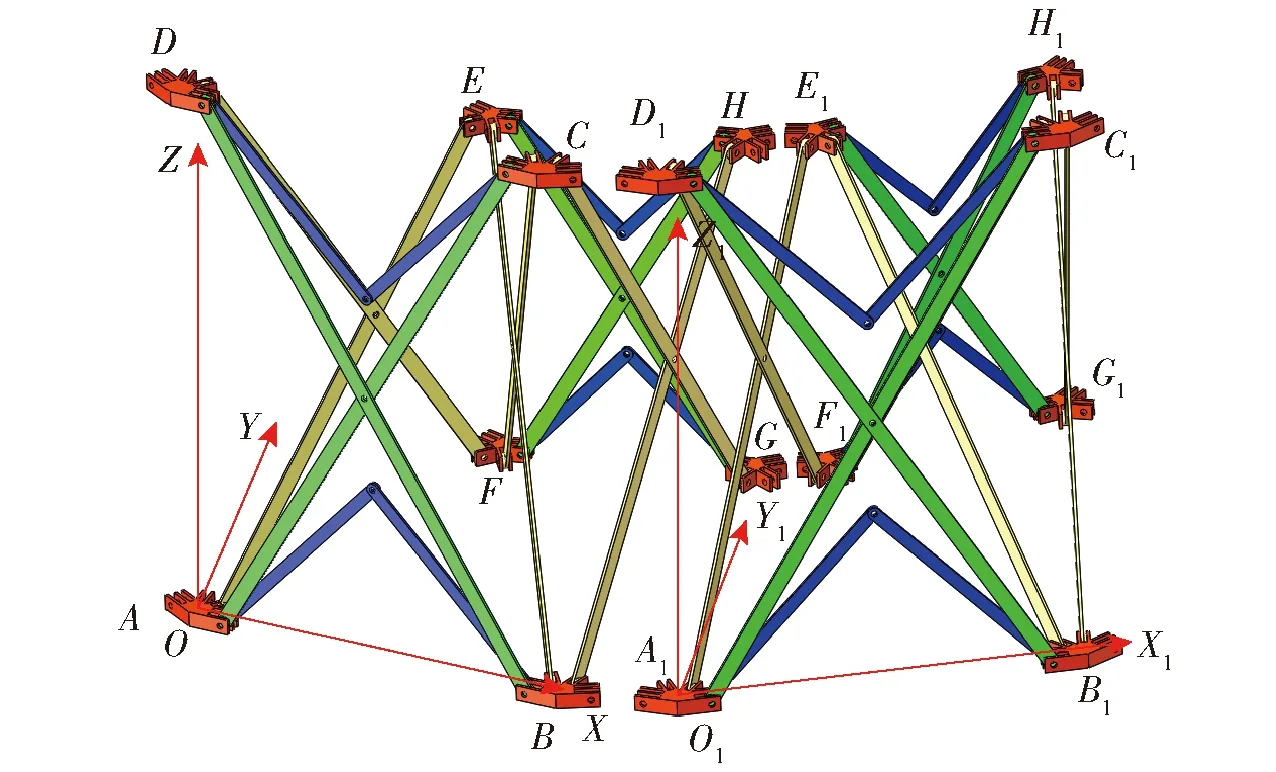
图10 2个单元机构及其坐标系
(9)
同理对于由N个单元机构组成的双环多杆天线展开机构进行分析,如图11所示任选其中一个单元机构建立全局坐标系,在其他剩余的N-1个单元机构相同位置处建立单元坐标系,由分析可知,假设相邻2个单元之间坐标系X轴之间的夹角为α,则α=360°/N,即α为旋转角,N个单元机构组成的双环多杆天线展开机构中由第j坐标系向第j+1坐标系转换只需绕Z轴逆时针旋转α即可,旋转变换矩阵由α组成。

图11 双环多杆天线展开机构及其坐标系
则在全局坐标系中各个构件速度为
(10)
其中
(11)
式中j——单元坐标系序号
i——第j个单元坐标系中构件序号
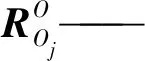
2.3 雅可比矩阵求解
由2.2节分析可知双环多杆天线展开机构由多种构件组成,则任意构件i的空间位姿表达式为
(12)
式中pi——构件i空间位姿
βi——构件i姿态角
对式(12)求导可得
(13)
式中Ji(φ)——构件i速度雅可比矩阵
φ——驱动角函数,即驱动输入
3 双环多杆天线展开机构加速度分析
根据螺旋理论可得螺旋加速度表达式为
(14)
式中Ai——构件i上单元坐标系原点重合点的六维加速度
εi——构件i上单元坐标系原点重合点的角加速度
ai——构件i质心处线加速度,由螺旋加速度表达式分析可知其后3项去除了构件i的向心加速度
多刚体系统螺旋加速度合成法则为
(15)
式中 Lie[]——李括号运算
如图8在封闭单元机构约束图中闭环Ⅰ可得
(16)
其中
(17)
式中εi——转动副i角加速度
由式(16)可得
(18)
同理在图8中的闭环Ⅱ~Ⅴ以及图9中的闭环Ⅰ~Ⅴ也可以得到螺旋加速度方程,在已知输入角加速度ε1的情况下,通过求解式(18)及其他螺旋加速度方程,便可以求解出单元机构中构件i的螺旋加速度。
在求解出构件i的螺旋加速度之后,提取其前3项,便可以得到构件i的角加速度为
εi=ξ(Ai)
(19)
式中ξ(·)——提取螺旋加速度的前3项
在求解出构件i的角加速度之后,根据螺旋加速度的物理意义,可以得到构件i质心线加速度为
ai=ζ(Ai)+ivi+iri+i(iri)
(20)
式中ζ(·)——提取螺旋加速度后3项
与之前速度求解过程一样各个单元机构中位置相同的构件在单元坐标系下加速度相同,则单元机构中构件i的加速度在全局坐标系j中的表达式为
(21)
至此,得到了双环多杆天线展开机构中各个构件在全局坐标系下角速度、角加速度的表达式。
4 动力学分析与模拟仿真
4.1 动力学建模
采用拉格朗日法建立可展开天线机构动力学方程。可展开天线机构为单自由度机构,设外连接杆与外环节点之间的夹角为φ,选取输入角φ作为广义坐标。则可展开天线机构的动力学方程为
(22)
式中ET、EU、Q——动能、势能以及广义坐标对应的广义驱动力
由第2节双环多杆天线展开机构速度分析可知,外环节点A在全局坐标系中固定,其他内外节点在全局坐标系中做平移运动,剩余构件在全局坐标系中做平面运动,可展开天线机构中做平移运动的内外环节点总动能表达式为
(23)
式中mi——构件i的质量
做平面运动的构件总动能的表达式为
(24)
式中Ji——构件i绕过质心轴线转动的转动惯量
则可展开天线机构总动能为
ET=T1+T2
(25)
宇航空间环境为微重力环境,这里暂不考虑重力作用,因此可展开天线机构的势能EU=0,将驱动角函数代入式(22),即可求出广义坐标所对应的广义驱动力。
4.2 模拟仿真与理论计算验证
为了验证理论推导的正确性,通过仿真软件ADAMS和计算软件Matlab进行模拟仿真与数值计算,仿真模型中各构件参数如表1所示。如图12所示,在选定位置处添加一个驱动进行模拟仿真。双环多杆天线展开机构的展开过程如图12~14所示。

表1 各个构件物理参数

图12 完全收拢状态
图12为可展开天线机构完全收拢时的状态,此时可展开天线机构中相邻2个内环节点之间和相邻2个外环节点之间完全靠拢,可展开天线机构的体积最小,随着可展开天线机构逐渐展开,相邻内环节点和相邻外环节点之间的距离不断增大。图13为可展开天线机构半展开状态,此时机构中相邻2个内环节点之间和相邻2个外环节点之间的距离逐渐加大。图14为可展开天线机构完全展开状态,体积达到最大,可展开天线机构中通过转动副相连接的2个内连接杆之间的夹角为180°,可展开天线机构处于奇异位形状态。
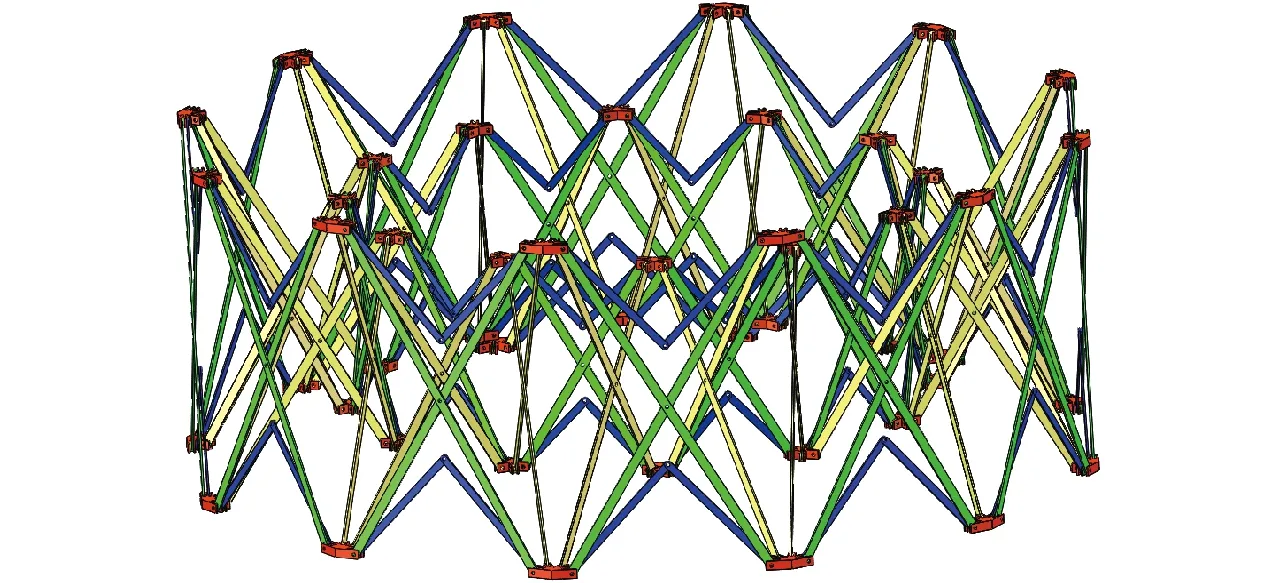
图13 半展开状态

图14 完全展开状态
选取单元坐标系与全局坐标系重合的单元机构中的内长杆、外连接杆、中间杆、内环节点为目标构件,4种构件沿X轴方向的运动学特性曲线的仿真结果与理论计算结果如图15~19所示。
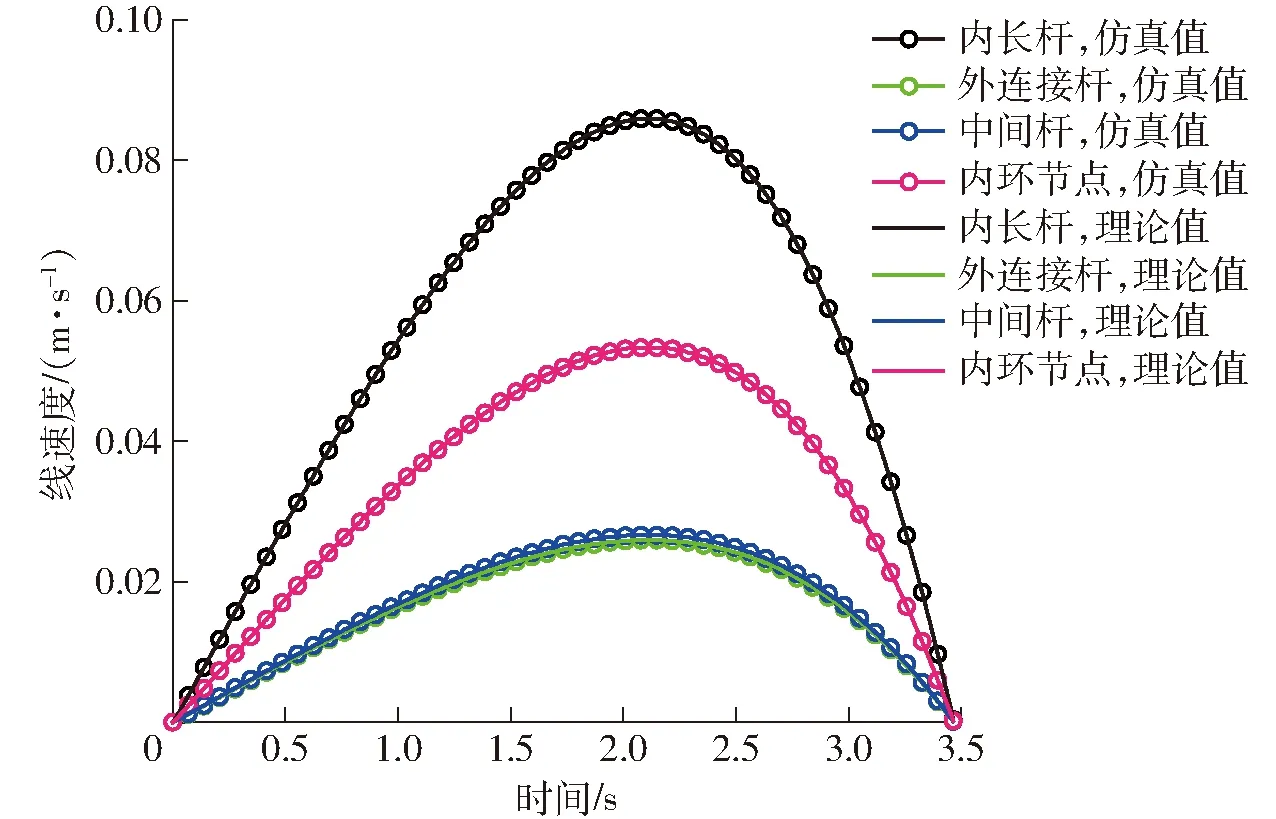
图15 各构件线速度
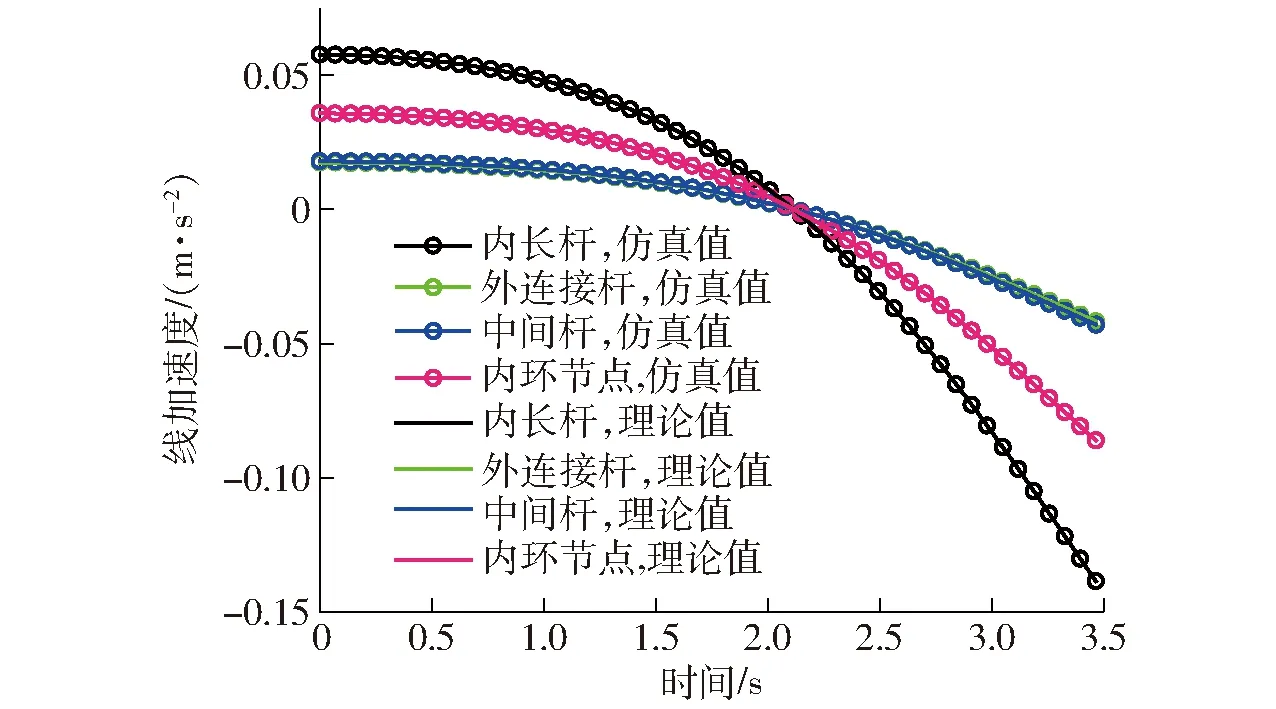
图16 各构件线加速度
由图15~19可知,模拟仿真结果曲线与理论推导结果曲线基本一致,表明了之前理论推导的正确性,基于螺旋理论和拉格朗日法相结合的动力学建模方法可较好地应用于此类空间可展开天线机构的分析中。由图15可知,4种构件沿X轴方向的速度均是先增加后减少,由图17、18可知,内环节点和外连接杆角速度、角加速度均为0,表明内环节点仅做直线移动不存在转动,外连接杆做绕Y轴的定轴转动运动。当时间接近3.5 s时理论计算失效,说明此时双环多杆天线展开机构处于完全展开状态并且处于奇异位形状态,理论分析与仿真结果相一致。由图15~18可知,各个构件角速度、角加速度、线速度以及线加速度曲线光滑,表明双环多杆天线展开机构展开过程动作平稳,不存在冲击与振动。
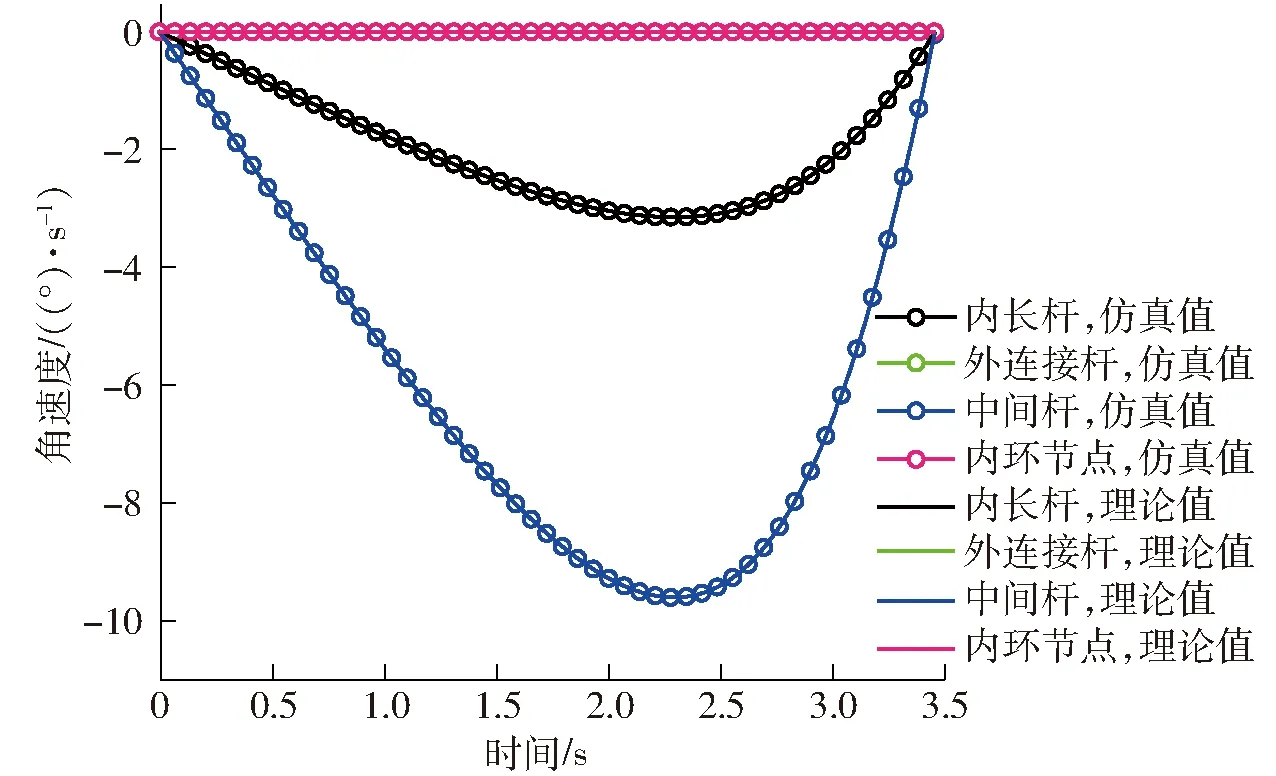
图17 各构件角速度
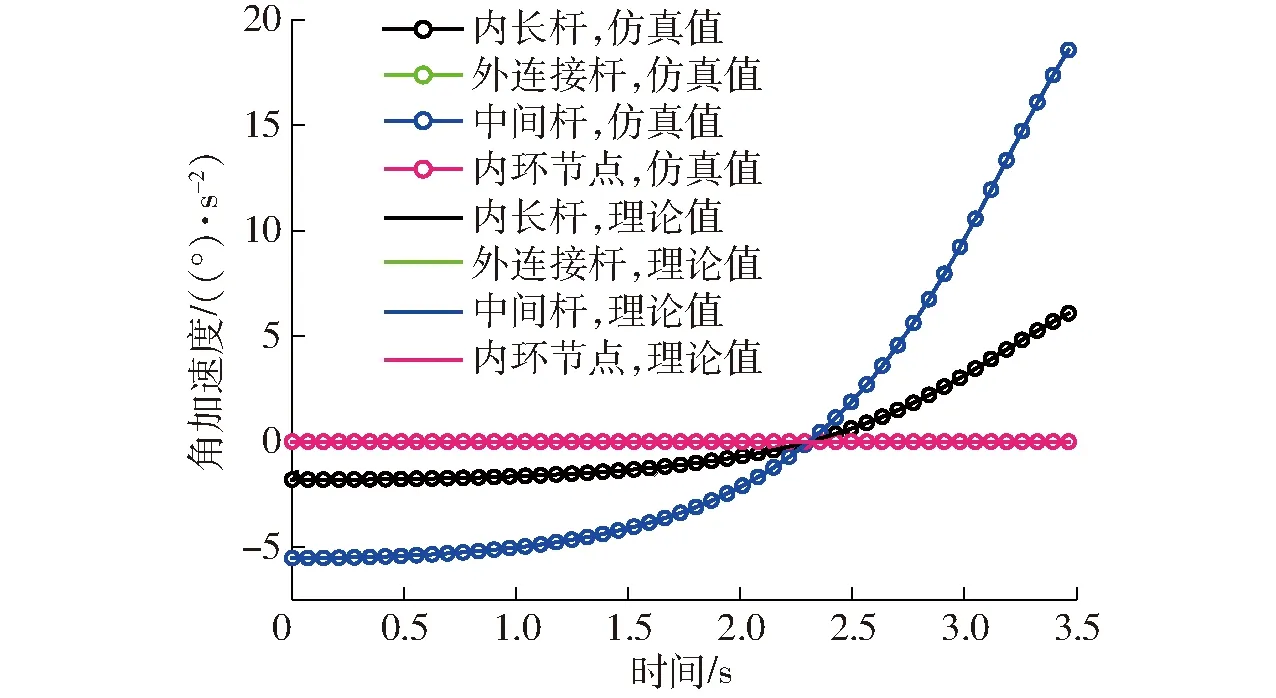
图18 各构件角加速度

图19 驱动力矩
5 结论
(1)基于螺旋理论和拉格朗日法相结合的方法建立了双环多杆天线展开机构的运动学与动力学模型,对双环多杆天线展开机构的运动学与动力学特性进行了分析研究,并通过理论计算结果与仿真结果对比,验证了理论推导的正确性。
(2)研究的双环多杆天线展开机构为单自由度机构,整体结构简单,仅需一个驱动便可展开。通过理论计算与模拟仿真分析,结果表明双环多杆天线展开机构整体展开过程平稳,可作为星载大口径可展开天线机构的支撑机构。
