变限积分函数若干问题的探讨*
2023-05-28王玉磊李彩娟苑倩倩
王玉磊 李彩娟 苑倩倩
(信阳学院数学与统计学院)
一、引言
在高等数学教材中涉及变限积分函数这一知识点的地方不是太多,如果教师不能及时拓宽知识面,那么学生对这方面内容的理解就仅局限于定义及其基本的求导公式的简单应用[1-2]。在教学过程中,发现学生对这方面的知识了解的不够,尤其是变限积分函数变化型的求导方法掌握欠佳,容易出错。关于变限积分函数的导数问题的研究,文献[3-7]已经从常见的变限积分函数及含参量积分函数两个方面给出了一些相对较好的结果,这为学生能更好的掌握变限积分函数求导提供了相应保证,但是对于涉及变限积分函数在其它问题方面的应用却不是很多,因此学生在遇到稍微综合性的题目时,往往不能够灵活应用,从容应对。本文结合具体问题归纳总结了变限积分函数在求分段函数的不定积分、积分换序及证明积分不等式等不同方面的应用,目的是帮助学生进一步理解变限积分函数的实质和内涵,为学生更好的掌握该知识点提供一定的参考。
二、概念与定理
在高等数学教材中,有如下的定义及定理:
定义1[1]设函数f(x) 是区间[a,b] 上的可积函数,则由
定义了一个以积分上限x为自变量的函数,称为变上限的定积分,也称变上限积分函数。
不难看出,变上限积分函数φ(x) 和变下限积分函数ψ(x) 是函数F(x) 取特殊值时的变限积分函数。
定理1[2]设f(x)为连续函数,u(x) 与v(x) 均为可导函数,且可实行复合f◦u与f◦v,则也可导,且
特别地,如果将F(x) 分别换成φ(x) 和ψ(x) ,也能得到类似的结果。定理2[3]设f(x,t),在区间[a,b] 上连续,φ(x) ,ψ(x)在区间[a,b] 上可导,则函数在区间[a,b]上也可导,且
在该定理中,如果将被积函数的积分上限或者积分下限换成常数,也可以相应的结果。
三、应用举例
(一)分段函数的不定积分问题
在学生学习该知识点的过程中,发现他们在求解分段函数的不定积分时,要么把要积分限变量与积分变量的取值范围搞混淆,要么不知道该如何选择被积函数相应的表达式,最终导致结果出现错误。通常在处理这种问题时,首先从积分限变量的取值入手,找到分段函数变量的分段点,然后将积分限变量的取值范围分成若干区间,最后在每一个区间上分别做定积分。尤其要注意当积分限变量与积分变量的取值在同一范围内或者积分限变量取值大于积分变量取值的最大值时,需要通过区间可加性将原积分再分成两个积分。
例1 设函数
解 当0≤x≤1 时,
当1 因此, 注 积分变量的取值范围及积分限变量的取值是解决这类问题的重点。该题型常出现在由密度函数求分布函数中。 变限积分函数的求导问题一直是教师在教学中的一个重要内容,当被积函数表达式变得复杂时,对它求导的难度也就随之增大。变限积分函数在研究生入学考试及各类数学竞赛中经常出现,对它进行求导也尤其重要,但是因其形式多变,不易求解,很多学生不能很好的掌握处理这类问题的方法。下面将对变限积分函数的求导问题分成三个方面,通过具体的实例求解进行方法探究。 1.直接求导 如果变限积分函数中的被积函数只是纯粹关于积分变量的函数,那么直接借助定理1 进行求导即可,但是公式不要记错,尤其是积分下限是一个函数时,一定要注意在积分下限函数代入被积函数再乘以积分下限函数之后,前面的符号应该是减号。这种类型往往比较简单,只要细心便不会出错,这里不再举例。 2.换元后求导 如果变限积分函数的被积函数是关于积分限变量与积分变量的函数,我们就不能盲目的直接利用定理1 对其进行求导。这时需要先考查被积函数表达式的构造形式,若被积函数表达式是可以直接将积分限变量与积分变量分离的函数,则只需先将含有积分限变量的那一部分直接写到积分号外面,然后根据乘积函数的求导法则直接进行求导即可;若被积函数表达式是不能直接将积分限变量与积分变量分离的函数,一般需要先通过换元法,将两个变量分离,之后再利用乘积函数的求导法则进行求导。当然对于上述两种类型也可以不用将被积函数表达式变量分离,直接利用定理2 的求导公式进行求导。 类型I 被积函数可直接变量分离 例2 设函数f(x)连续,求f)1( . 解 因为 又当x=1 时, 注 该题目也可以直接利用定理2,无需变量分离,直接对x求导后得到φ′(x) 的具体表达式。对于该类型,这两种方法均可以快速求解,学生只需根据自身实际情况选择一种方法即可。 类型II 被积函数不可直接变量分离 例3[4]设函数f(x)连续,且f(0 )≠0, 注 本例也可以利用定理2进行求解,具体可以参照文献[4]的结果,但是文献[4]在利用定理2 求导后,并不能最终避免变量替换的步骤,同样还是需要利用换元法进一步转换。相比之下,用上述先换元再求导的解法求解会更直接了当,更有利于学生掌握。 虽然上述两个例题均可以利用定理1 和定理2 进行处理导数问题,但是不难发现,当变限积分函数的被积函数为具体函数时,两种方法都可以,用利用定理2 进行求解也是很简洁的;当变限积分函数的被积函数含有等 这些形式函数时,我们直接利用换元法求解会更方便一些。 3.拆分再求导 被积函数含有绝对值的积分问题是学生最容易出错的一种类型,学生在处理这种问题时,往往无从下手,不知道用什么方式解决.其实这类问题的处理方法与求解分段函数的不定积分相似,抓住该问题的本质,首先要根据积分限变量与积分变量的取值范围将积分变量的区间进行拆分,其次把所求积分成若干个积分(去绝对值),再次利用变限积分的求导公式求函数的导数,最后利用极值的第二充要条件进行判定。 解 令I′(t)=0, 在求解一些定积分时,如果被积函数是一个关于变限积分函数的表达式,那么所求的定积分也可以看成是一种累次积分。当累次积分中里面一层不容易积分时,我们可采用交换积分次序来进行求解。 解 在全国研究生数学考试中,对微分中值定理的考查经常是以证明题的形式出现,解决这种问题最大的难点就在于对辅助函数的构造,下面就给出一种可以构造变限积分函数为辅助函数的例子,用以说明该部分内容。 证 明: 在(0,)π内 至 少存 在 两 个 不 同 的 点1ξ,2ξ,使 对h(x)在[0 ,]π上应用罗尔定理,可知存在η∈(0,)π,使 得从而g(η)=0. 在[ ]η,0 和[ ]πη, 上对g(x) 应用罗尔定理, 注 在一般情况下,对于判断函数的零点问题,往往利用零点定理和函数的单调性就能解决,但是如果所给题目中只给出了“函数在某区间上连续”的条件或者在证明题当中的条件或结论涉及到的是定积分,那么我们可以优先考虑构造变限积分函数为辅助函数。 积分不等式的证明也是全国研究生数学考试中一个考查的知识点。处理这种问题时,常常需要较多的技巧,不易总结其规律,但是有一些积分不等式可以采取常数变量化的思想进行证明。一般分为三个步骤:首先利用变限积分函数构造合适的辅助函数,然后对变限积分函数进行求导,最后再通过函数单调性达到问题的证明。这种证明方法思路清晰,构造辅助函数的方法规律也较明显,可以提高学生学习高等数学的能力。 证明 令 则 又F(a)=0, 注 欲证明这类问题,先要观察不等式左右两边的上下限,根据变上限积分下限固定上限变化的特点,构造变限积分函数F(x),再对其求导,通过单调性的判别法则可以得到函数F(x)的单调性,最后在所给区间上应用单调性的定义即证。可见,构造合适的变上限积分函数是证明这类题目的关键。 分清积分限变量与积分变量是学习变限积分函数的基础。理解变限积分函数的含义,掌握变限积分函数求导理论并熟练使用公式做题是教学上的一个重要任务。在讲述这一知识点时,教师在课堂上可以借助几何图形,从定积分的几何意义入手,通过对定积分的分析进而引导学生发现变限积分函数的规律,在课后也可以将与变限积分函数相关的知识进一步归纳整理,让学生通过实战练习逐步形成一种定势思维,使学生能够有效的运用所学知识解决这方面的难题,最终达到提高学生学习效果的目的。(二)变限积分函数求导问题
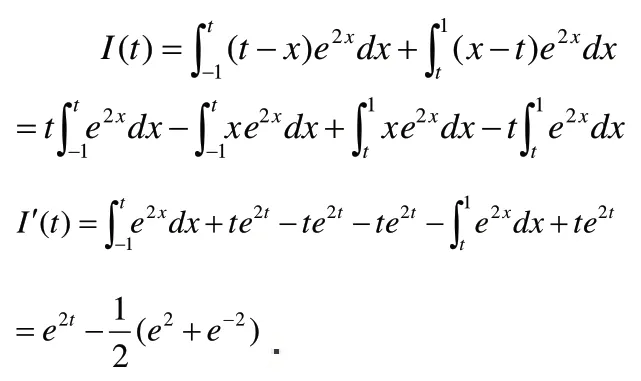
(三)变限积分换序问题
(四)用变限积分函数构造辅助函数的问题
(五)构造变限积分函数证明积分不等式的问题
四、结语
