承压含水层非达西变速抽水井流模型研究

2023-05-27肖良宗一杰甘富万陈立华

广西大学学报（自然科学版） 2023年2期

肖良, 宗一杰, 甘富万, 陈立华*

(1.广西大学土木建筑工程学院, 广西南宁 530004;2.广西防灾减灾与工程安全重点实验室, 广西南宁 530004;3.工程防灾与结构安全教育部重点实验室, 广西南宁 530004)

0 引言

定流量抽水试验自上个世纪以来已得到了广泛的研究[1-3],然而,越来越多的相关工程表明[4]:在实际抽水过程中,抽水流量不可能完全稳定。抽水流量的变化可能是水和管道之间的摩擦[5]、电机升温导致效率降低或其他水头损失所引起的结果。此外,还存在刻意改变抽水流量的做法,以便在实际工程中更好地分析含水层参数敏感性[3],因此,可以认为一个实用的变速抽水模型在许多领域中具有着广泛的工程需求。

自上世纪60年代以来,变速抽水试验已经得到了大量水文地质学家的关注[6-8]。Mahmoud等[6]首先研究了抽水井流量随着水位下降而下降的情况。此后,又有大量学者为特定条件下的变速抽水试验推求了解析解和数值解[4,9-11]。为了可以更好地近似模拟不同条件下的变速抽水试验,迄今为止已经有许多计算方法被提出,主要包括指数关系近似[5-6]、分段线性关系近似[10,12]和叠加原理近似[2,13],其中,叠加原理所得到的计算公式在实际应用中明显比其他方法更为简单。

前面提到的研究普遍假设地下水流遵循达西定律,然而,这种假设在部分多孔介质渗流中被发现是不合理的。例如在具有较宽缝隙的岩石中、致密的黏土中或具有较高渗透率的多孔介质中等情况[14]。此时比流量与水力梯度之间呈非线性关系,即出现非达西流。为了描述非达西流,前人已经开发了许多公式。其中,Forchheimer方程和Izbash方程是2种最为常用的方法[15]。Forchheimer 方程是一个具有经验系数的二阶多项式函数[15],Izbash方程则是一个将比流量表示为水力梯度的幂函数,被认为可以更方便地与达西流进行耦合[16]。2个方程的选用主要取决于具体的实际工程情况[15,17-21]。

Li 等[10]在考虑井储效应的情况下,首次提出了可用于变速抽水的非达西流解决方案,并将其与实际工程数据进行了对比,然而,他们的匹配结果表明,利用实测数据推求得到的在抽水井附近的渗透率和距离抽水井较远处的渗透率是不同的。据我们所知,这种偏差可能是由表皮区域的影响导致的。以往学者的研究表明,表皮效应会导致抽水井附近的渗透率出现变化[22],且考虑表皮区域的方案也可以显著增强其实用性[4,22]。迄今为止,仍未发现有针对非达西流条件下考虑表皮效应的变速抽水试验的研究。

由于钻井过程中泥浆或岩粉的侵入以及钻井后地球的化学沉淀或溶解作用,抽水井附近一般会存在表皮区域[22]。表皮区域的水力参数被认为与含水层原本的水力参数之间存在明显的不同,这也导致了表皮区域的存在将影响到抽水试验的降深时间曲线。这种现象被定义为表皮效应[23]。用于表皮区域渗流建模的最为常用的方法是有限厚度表皮法,过去的学者依据此方法已经对表皮效应进行了大量的研究。例如:Wen等[24]通过 Laplace 变换建立模型来考虑越流含水层的表皮效应;Yeh等[25]在承压含水层中进行了段塞试验,并得出了含水层存在表皮区时其表皮效应不可忽略的结论;Wen等[26]在3个不同的含水层-弱透水层系统中进行了定水头试验用以分析积极表皮和消极表皮的影响。这些研究人员认为,忽略表皮效应将给地下水渗流模型带来严重的误差。同时,还有其他学者注意到观测井的距离越近时表皮效应的影响越显著[27,28],因此,为了实际目的,有必要进一步研究井储和表皮效应对非达西流引起的变速抽水试验的综合影响。

本文考虑表皮效应和井储效应,提出了由变速抽水试验引起的非达西流的数值模型。该模型同时考虑表皮效应和井储效应的影响,采用 Izbash 方程描述非达西渗流的非线性,并用叠加原理和有限差分法推导出模型的数值解。通过与 COMSOL 的数值模拟进行对比,验证提出模型的可行性。

1 数学模型

考虑表皮效应和井储效应,承压含水层下考虑井储效应和表皮效应的变速抽水模型示意图如图 1 所示。其数学建模的基本假设如下:①该含水层是承压、均质、各向同性且厚度均匀的,抽水井和观测井均为完全渗透井;②含水层在水平方向上无限延伸,抽水前各点的水位降深为0;③在抽水井附近形成有限厚度的表皮区域;④抽水井的半径为固定值(正数),需要考虑抽水开始前井内已存在的蓄水量;⑤抽水引起的流动是非线性的;⑥抽水过程符合阶梯状的变速抽水。

图1 承压含水层下考虑井储效应和表皮效应的变速抽水模型示意图Fig.1 A schematic diagram of the variable-rate pumping test considering wellbore storage effect and skin effect in a confined aquifer

本文使用叠加原理求解变速抽水问题。叠加原理是依据抽水流量的变化过程,将一个变速抽水试验近似为多个在同一位置下的定流量抽水试验的共同作用,因此,基于有限差分的变速抽水问题的数值解推求过程可分为2个步骤:①推求定流量抽水时的数值解公式;②将多组不同流量下的定流量抽水公式进行组合,得到所需的变速抽水公式[2]。

首先推导出在考虑表皮和井储效应下的定流量非达西数值解。根据上述的基本假定,可以用公式(1a)和(1b)分别表示该定解问题中表皮区域和外部区域的控制方程。

(1a)

(1b)

式中:q1(r,t) 和q2(r,t) 分别为表皮和外部区域的比流量,量纲为[L/T];s1(r,t) 和s2(r,t) 分别为表皮和外部区域的降深,量纲为[L];S1和S2分别为表皮和外部区域的储水系数,且为无量纲数;r表示距抽水井的距离,量纲为[L];b表示含水层厚度,量纲为[L];t表示抽水时间,量纲为[T]。

其初始条件为

s1(r,0)=s2(r,0)=0。

(2)

在考虑井储效应的情况下,井壁处定流量边界条件[29]为

(3)

含水层水平方向上的无穷远边界条件为

s2(∞,t)=0。

(4)

在表皮和外部区域的交界面处,其边界条件为

q1|r→R=q2|r→R,

(5)

式中:R为表皮区域的径向距离,其表示含水层内表皮和外部区域的交界面处距抽水井的距离,量纲为[L]。

基于Izbash方程,可将表皮与外部区域的比流量分别表示为

(6a)

(6b)

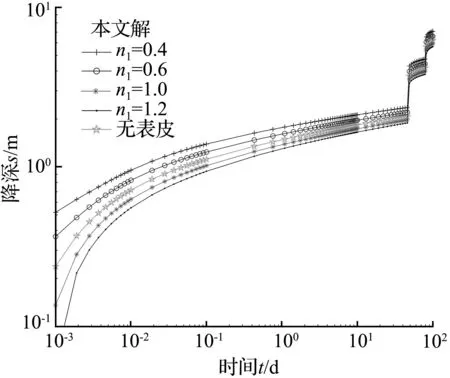
式中:K1和K2分别为表皮和外部区域的准渗透率,量纲分别为[Ln1/Tn1]和[Ln2/Tn2];n1和n2分别为表皮和外部区域的非达西系数,均为无量纲常数。此外:当非达西系数n<1 时,该渗流为前达西流;如果 1

将式(6a)、(6b)对应代入式(1a)、(1b),可得到新的控制方程为

(7a)

(7b)

此时令定流量抽水的流量值固定为Q,量纲为[L3/T],则可以引入式(8)来对方程(7a)、(7b)进行线性处理。

(8)

该等式表示在单位时间内通过距含水层任一距离的径向面的水量均约等于Q。前人研究表明在分析抽水井附近位置或抽水后期时,此近似的误差很小[16]。

结合公式(7a)、(7b)和(8),可以得到表皮和外部区域的控制方程分别为

(9a)

(9b)

2 基于有限差分的数值解

本文采用有限差分法用于推求所需方程的数值解。该方法需要先对模型进行两点处理:第一步,用一个很大的固定半径值re去代替无穷远边界,将原本的抽水模型概化为一个以时间t和半径r作为因变量的二维模型;第二步,对于径向空间 [rw,re] 和时间区间 [0,t] 分别离散为J和N个步长。其中,在径向坐标上任何一个节点j处的径向距离rj均满足rw≤rj≤re,j=0,1,2,…,J,而时间坐标上任何一个节点n处的时间值tn则必满足 0≤tn≤t,n=0,1,2,…,N。具体的步长如下:

(10a)

(10b)

式中:Δt表示任意2个相邻时间节点之间的步长,量纲为[T];Δr表示任意2个相邻径向节点之间的步长,量纲为[L]。

依照有限差分法的隐式公式[30],可以得到

(11a)

(11b)

(11c)

(11d)

(11e)

(11f)

把公式(11a)-(11f)代入方程(2)、(3)、(4)、(9a)和(9b)之中,可以得到

(12a)

(12b)

(13)

(14)

(15)

其中:

(16a)

(16b)

(16c)

(16d)

(16e)

(16f)

之后将公式(12a)-(16f)代入MATLAB软件中,选取合适的步长,即可自动求得在各个结点上的降深值。在rj≤R的节点上选用方程(12a)计算得到的结果,在rj>R的节点上选用方程(12b)计算得到的结果,即可求得在假设的定流量试验条件下的任意点降深情况。

图2 变速抽水试验示意图Fig.2 Schematic diagram of the variable-rate pumping test

然后基于方程(12a)和(12b),可以推导得出所需的非达西变速抽水试验的数值解。根据叠加原理,假设抽水流量仅在有限数量的离散时间点发生变化[2],如图 2 所示。抽水总降深等于各个流量变量单独产生的降深值的代数和[13],它可以表示为

(17)

式中:m表示抽水时期数,即流量变量的数量;s表示全部m个抽水时期的总降深,量纲为[L];Δsk(ΔQk,Δtk) 表示由第k个流量变量单独产生的降深,量纲为[L]。 Δtk表示第k个抽水时期的持续时间,量纲为[T];ΔQk为第k个抽水变量,其参数值等于Qk-Qk-1。Qk表示的是如图 2 所示的第k个抽水时期的流量值,量纲为[L3/T]。特别注意Q0=0。

由此可知,若将定流量抽水公式(12a)和(12b)所求得的,在流量为Q、抽水时长为t时的降深分别用s1(Q,t) 和s2(Q,t) 表示,则依据公式(17)所推得的表皮和外部区域的变速抽水公式分别为

(18a)

(18b)

其中:

(19a)

(19b)

3 验证与讨论

3.1 验证

为了研究所提出数值解的准确性,将方程(2)、(3)、(4)、(7a) 和(7b) 代入模拟软件 COMSOL Multiphysics 之中,通过有限元的方法进行数值模拟用以进行验证。在该模拟中,根据现实中实际存在的含水层情况提出了一个假设案例,并分别代入求出本文的有限差分解和 COMSOL 解,将二者进行比较来研究提出解的可靠性。该案例假设含水层为细粒介质,此时抽水产生的渗流往往遵循非达西定律[31]。根据已有的研究,细砂条件下渗透率为1～5 m3/d,承压含水层的储水系数一般在0.000 05～0.005范围内取值[14]。各假设案例对应水力参数值见表1。本文合理地选择了一组参数,其各参数值见表1中的案例A所示。

案例中假设有3个抽水时期,各时期的抽水持续时间分别为46.3、34.7、19 d。选取R为10 m,分别在表皮和外部区域设置r为9、20 m 的观测井用以分别验证公式(18a)和(18b),并将二井的本文解与 COMSOL 解比对结果分别绘制在图 3(a) 和图 3(b) 中。结果表明,在抽水期间,所提出的数值解的降深-时间曲线与 COMSOL 解的结果吻合得很好,仅在曲线出现较大波动的2处位置拟合效果存在一定偏差。考虑到这2处波动是变速抽水模型中的2次抽水流量的改变所导致的,这种偏差应该可以认为是COMSOL模型中流量突变时为了保证收敛性而导致的结果。图3所展示的对比结果可以证明本文提出方案对于表皮和外部区域的降深模拟均具备实用性。

表1 各假设案例对应水力参数值Tab.1 Parameter values of each hypothetical cases

(a) 表皮区域

(b) 外部区域

3.2 结果与讨论

在本节中,通过假设案例进一步讨论了由n1、K1和R为代表的表皮效应对于降深的影响。表1中给出了各假设案例的参数值,降深随表皮区参数的变化如图4所示。考虑到为了更直观地进行对比,在3组对比结果中均额外绘制了不考虑表皮效应的降深-时间曲线,即在相应案例情况下使K1和n1值分别等于K2和n2值的曲线。与图3类似,图4(a)、4(b)和4(c)中的降深-时间曲线均出现了两处明显的突变,这同样是由于3个假设案例在抽水过程中存在的两次流量突变而导致的。

图4(a) 显示了n1在案例B情况下对表皮区域降深值的影响。图 4(a) 中,随着n1值的增加,降深值逐渐减小。与之类似,作者发现在图 4(b) 中,案例C条件下各时刻的降深值与K1值也具有负相关关系。从物理上来说,这是可以理解的:在抽水刚开始时,补给水主要来自于含水层的弹性蓄水。在这种情况下,较大的n1和K1值会加速弹性蓄水的释放。随着抽水的继续,抽水井附近的弹性蓄水基本释放完毕,此时抽出的水主要来自于外围较远区域的补给。而K1或n1越大,则导致含水层中水的输送过程越容易,从而对应地导致了水的补给速度加快以及降深值减小。

图4(c) 显示了案例D条件下不同R值对应的降深时间曲线。结果表明R值变化的影响主要针对于抽水前期。随着抽水时间的增加,这种影响会逐渐减弱。同时,还应注意到当r