低周反复荷载作用下钢管自应力钢渣混凝土柱弯矩-曲率关系数值分析*

于 峰 陈 昊 姚 弛 秦 尹 方 圆 卜双双

(安徽工业大学建筑工程学院, 安徽马鞍山 243002)

钢管混凝土结构在受压时会产生“套箍效应”[1-2],内部混凝土呈现三向受力状态,进而使结构整体得到较高的承载力和稳定性。然而,工程实践表明:核心混凝土在硬化过程中将产生体积收缩,致使外部钢管与混凝土存在脱空现象,[3-4]对钢管混凝土组合结构的各项性能都产生很大折减。

针对钢管混凝土结构的脱空问题,有学者采用膨胀混凝土作为核心混凝土,形成“钢管自应力混凝土结构”[5-6]。由于钢管的约束性,核心混凝土硬化膨胀后会产生结构预应力,提前进入三向受压状态,弥补传统钢管混凝土内部收缩与脱空的缺陷。但市场上现有的膨胀剂存在膨胀率小、掺量大、成本高等缺点,[7-8]限制了钢管自应力混凝土结构的应用。

钢渣作为钢铁生产的工业废渣,成分以钙、镁、铁等元素的氧化物为主。[9-10]可将钢渣用于替代传统混凝土集料,制备的钢渣混凝土具备高强度和高耐久的优点。[11-12]同时,由于其本身富含游离的MgO和CaO,水化时易产生体积膨胀,[13]国内外学者对钢渣混凝土的膨胀性能开展了相关研究。于峰制备了全钢渣砂混凝土,并对其膨胀率和基本性能展开研究,研究[14]表明:钢渣混凝土具有良好的和易性和抗压强度,可以实现钢渣混凝土膨胀率的合理控制。因此,利用钢渣混凝土代替原成本较高的自应力混凝土,不仅能实现工业废弃物再利用,保护环境和自然资源,降低工程造价,还为普通钢管混凝土的脱空缺陷提供了合理的解决方案,进而实现钢管与自应力钢渣混凝土的有机结合。Yu等开展10根钢管自应力钢渣混凝土短柱轴压性能试验研究,结果[15]表明:钢管自应力钢渣混凝土短柱在轴压作用下均呈现鼓曲状压弯破坏;随着钢渣混凝土膨胀率的增加,试件的承载力得到提高。Noureddine开展矩形钢渣混凝土柱静力性能试验研究,结果[16]表明:随着试件长度和偏心距的增加,承载力显著降低,钢管产生鼓曲环,试件整体产生局部屈曲破坏。

综上所述,国内外对钢管自应力钢渣混凝土柱已经有了一定的研究,包括其轴压性能、偏压性能以及钢渣混凝土膨胀率等方面,但对钢管自应力钢渣混凝土柱抗震性能方面的研究甚少。为此,在抗震性能试验[17]的基础上,开展钢管自应力钢渣混凝土柱弯矩-曲率关系全过程分析,分析轴压比、混凝土抗压强度、钢材屈服强度等参数对弯矩-曲率骨架曲线的影响,通过编制的MATLAB非线性分析程序得到计算值,且与试验值进行比较。

1 试验概况

试验设计了10根钢管自应力钢渣混凝土柱和4根钢管钢渣混凝土柱,考虑了试件的轴压比、径厚比、剪跨比、钢渣混凝土膨胀率参数影响,试件参数如表1所示。试件总高为1 600 mm,柱头和基础尺寸分别为400 mm×400 mm×400 mm,1 500 mm×400 mm×400 mm,柱区间段净高分别为400,600,800 mm。试件钢管采用外径219 mm的Q235直焊缝钢管,壁厚为2.85,3.73,4.88 mm。钢管底端焊接10 mm厚钢板,顶端焊接10 mm厚的开孔钢板。试验中钢管内的核心钢渣混凝土采用C35自应力钢渣混凝土和C35普通钢渣混凝土,基础和柱头采用C35普通商品混凝土,混凝土配合比及力学性能和膨胀性能如表2所示。此外,通过对25 d混凝土膨胀率的测量,得到普通钢渣混凝土和商品混凝土的膨胀率为-3.4×10-4,而自应力钢渣混凝土的膨胀率为1.11×10-3。试件尺寸和配筋如图1所示,其中纵向受力钢筋采用HRB400筋,箍筋采用HPB300筋。

表1 钢管自应力钢渣混凝土柱试件参数[17]Table 1 Experimental parameters of self-stressing steel-slag-concrete-filled steel tube columns

表2 混凝土配合比及力学性能试验值[17]Table 2 Mix proportions and mechanical properties of concrete in tests

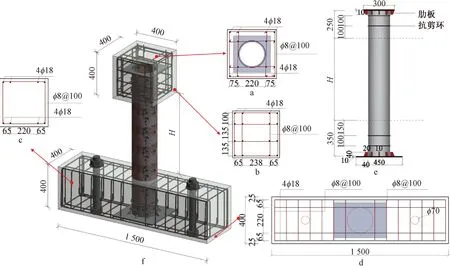
a—柱头顶部剖面; b—柱头侧剖面; c—基础侧剖面; d—基础底部剖面; e—试件尺寸。图1 试件尺寸和配筋[17] mmFig.1 Dimensions and reinforcement of specimens

2 试验结果

2.1 试件破坏形态

通过观察加载过程和试验结果,所有试件的破坏过程和现象大致相同,试件的受力过程经历了弹性阶段、弹塑性阶段和破坏阶段。以试件C1为例,在弹性阶段,试件的卸载和加载过程未产生残余变形,试件外观均无明显现象;当试件的水平位移达到10 mm时,钢管发生屈服,试件进入弹塑性阶段,荷载增长速度放缓,且呈非线性增长。当水平位移达到20 mm后,可听到密集的闷响声;当荷载接近试件峰值承载力时,试件进入破坏阶段。试件整体呈现压弯破坏,柱底200 mm范围内钢管表面形成微鼓区,并逐渐发展成双向鼓曲环。试验结束后,将外层钢管剥离,可以观察到核心钢渣混凝土的破坏特征为:柱底50 mm范围内核心钢渣混凝土被压碎。与非自应力试件相比,自应力钢渣混凝土表面产生的裂缝宽度和深度均较小,自应力试件完整性较好。试件典型破坏形式如图2所示。

a—试件整体破坏形态; b—试件整体破坏面; c—钢渣混凝土破坏面; d—钢渣混凝土破坏形态。图2 试件破坏形态[17]Fig.2 Typical failure models of specimens

2.2 试验曲线

2.2.1弯矩-曲率骨架曲线特征

各试件的弯矩M-曲率κ骨架曲线的发展趋势基本相似,分为上升段和稳定段。以试件C1为例,弯矩-曲率骨架试验曲线如图3所示,在上升段,弯矩-曲率骨架曲线整体呈线性增长,曲线斜率较大,且随着弯矩增加,试件的曲率发展较慢。在弹性阶段末期,水平位移持续增加,当试件弯矩达到极限弯矩的61%～73%,试件屈服。此时,试件弯矩增长速度减小,曲线出现明显拐点,曲线斜率开始减小,试件刚度降低。试件屈服后,进入稳定段。随着弯矩继续增加,曲率迅速发展,直至弯矩-曲率骨架曲线斜率为零,随后试件弯矩基本不变,试件发生破坏。

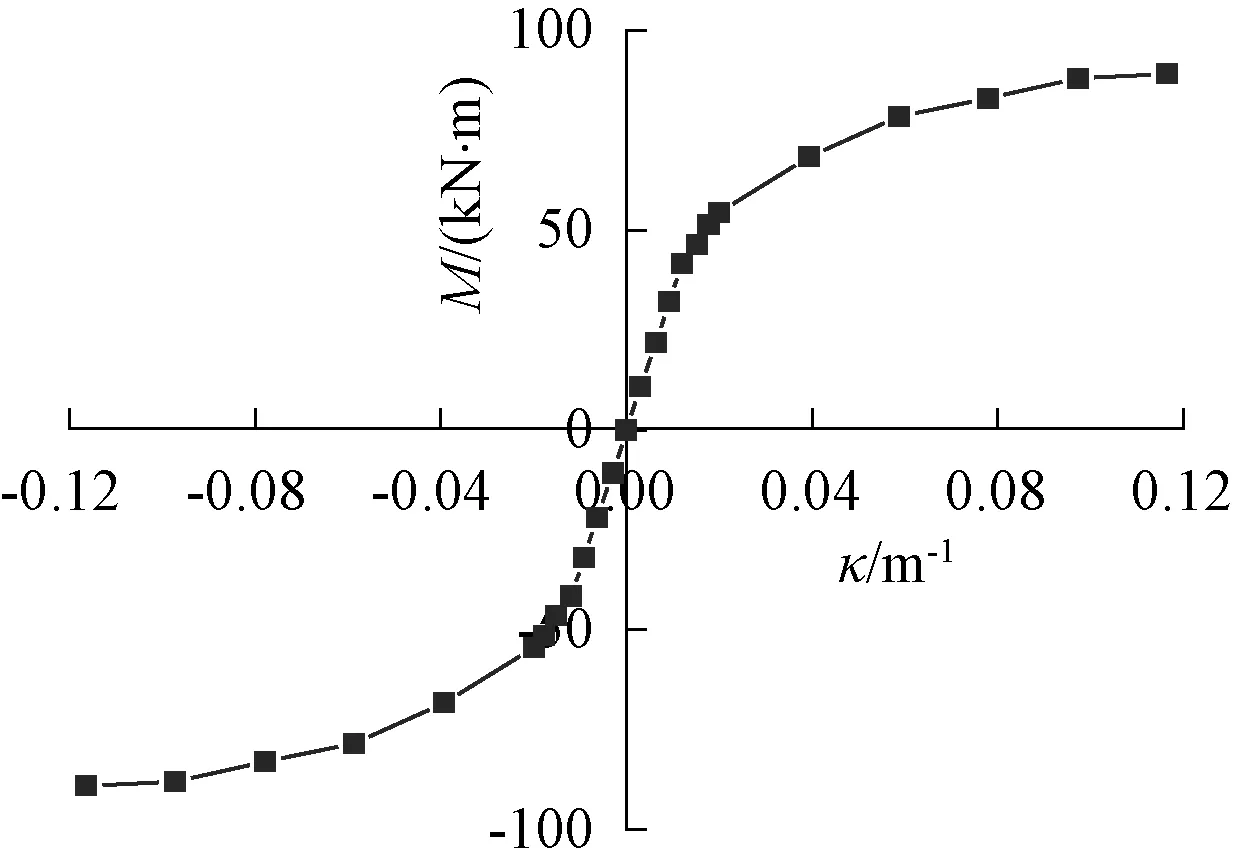
图3 试件弯矩-曲率骨架曲线Fig.3 Moment-curvature skeleton curves of specimens

2.2.2影响因素分析

1)轴压比的影响。图4为轴压比对试件弯矩-曲率骨架曲线的影响。从中可以看出:在上升段,随着轴压比增加,试件弯矩-曲率骨架曲线斜率微增,屈服弯矩增加,屈服曲率减小,试件处于弹性工作状态。这是因为随着轴压比增加,核心钢渣混凝土受到外钢管的约束效应增加,抵抗外部弯矩的能力增强,而此时试件曲率较小,附加弯矩影响不明显。在稳定段,随着轴压比增加,试件弯矩-曲率骨架曲线弯矩斜率增加,弯矩增长速度增加,极限弯矩增加,极限曲率减小。这是因为随轴压比增加,核心钢渣混凝土受到外钢管的约束效应增强,试件抵抗弯矩的能力增加,极限弯矩增加。且由于轴压比增加,试件承担轴压力引起的附加弯矩增加,试件破坏速度增加,极限曲率减小,变形能力减弱。

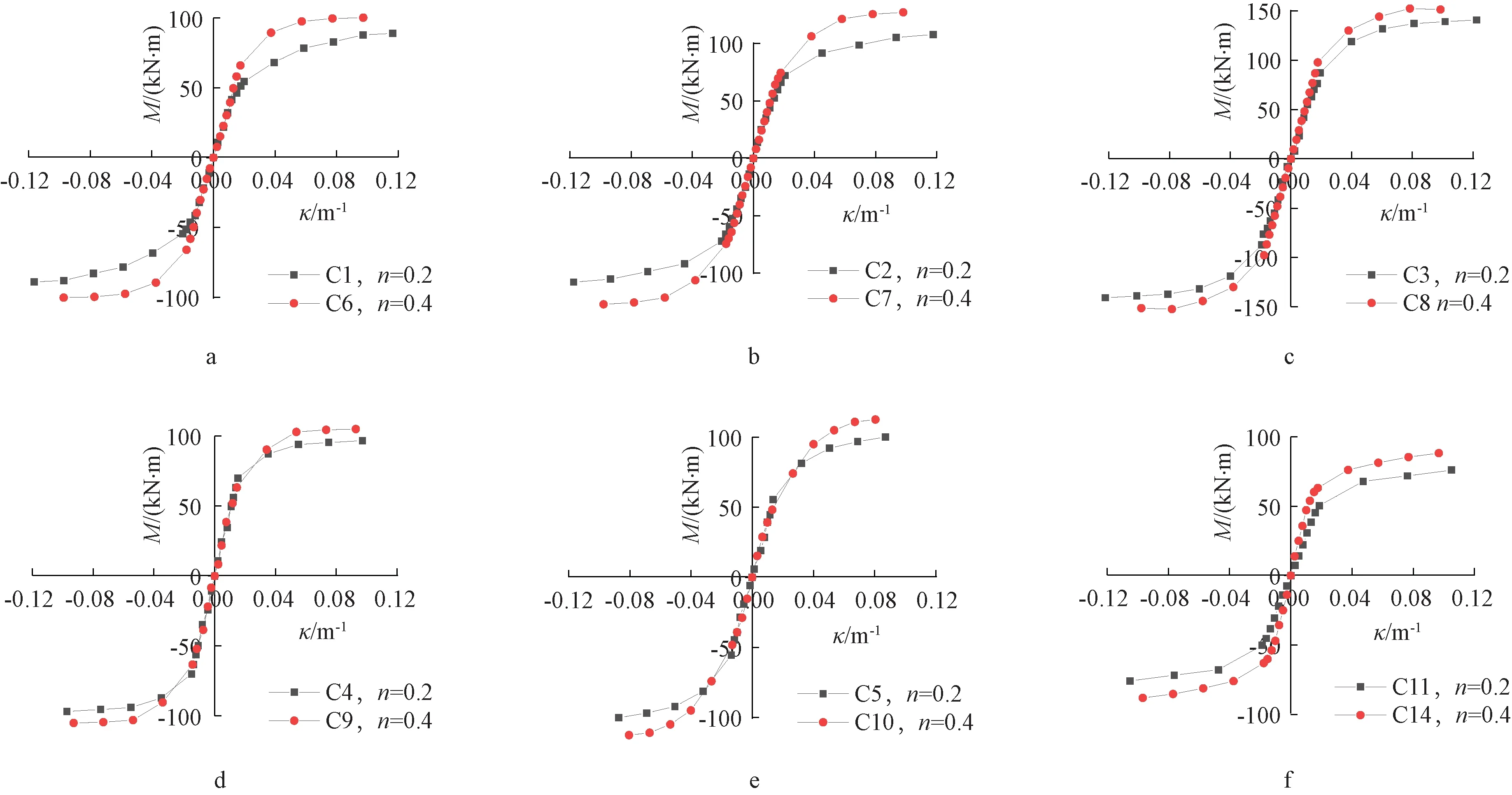
a—径厚比为76.84; b—径厚比为58.71; c—径厚比为4.88; d—剪跨比为1.37; e—剪跨比为0.91; f—钢渣混凝土膨胀率为-3.4×10-4。图4 轴压比的影响Fig.4 Effects of axial compression ratios

2)剪跨比的影响。图5为剪跨比对试件弯矩-曲率骨架曲线的影响。从中可以看出:在试件受力各阶段,随着剪跨比增加,试件极限曲率增加,抗弯承载力无明显影响。这是因为抗弯刚度只与试件的截面惯性矩及弹性模量有关,与试件高度无关。因此,在曲率相同时,试件各阶段抗弯承载力基本相同。随着剪跨比减小,试件的有效高度减小,试件破坏过程越急促,变形越不充分,极限曲率减小。

a—轴压比为0.2; b—轴压比为0.4; c—钢渣混凝土膨胀率为-3.4×10-4。图5 剪跨比的影响Fig.5 Effects of ratios of shear spans to effective depths

3)径厚比的影响。图6为径厚比对试件弯矩-曲率骨架曲线的影响,从中可以看出:在上升段,试件处于弹性工作状态,随着径厚比的减小,骨架曲线斜率增加,初始刚度增加,屈服弯矩增加。这是因为,随着径厚比减小,试件含钢率增加,核心钢渣混凝土受到外钢管的约束效应增加,试件抵抗弯矩能力增强,抗弯承载力增加,屈服弯矩增加。在稳定阶段,随着径厚比减小,试件弯矩-曲率骨架曲线斜率基本一致,极限弯矩增加,极限曲率无明显影响。这是因为在弹塑性阶段及塑性阶段,外钢管逐渐屈服,核心钢渣混凝土承担的弯矩增加。在此阶段,随着径厚比减小,外钢管的约束效果逐渐接近,对核心钢渣混凝土裂缝发展影响较小,试件弯矩-曲率骨架曲线斜率基本一致,极限曲率无明显影响。

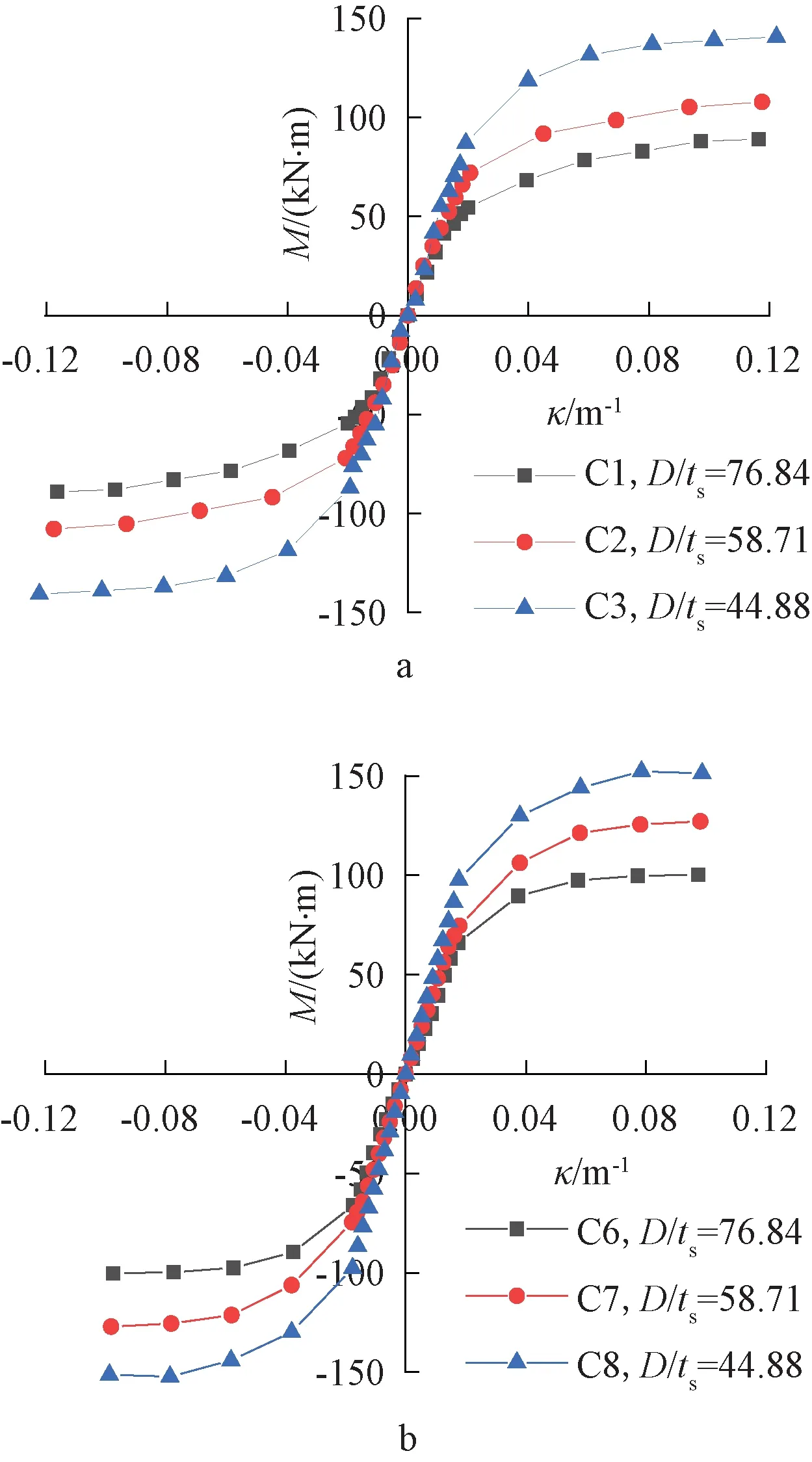
a—轴压比为0.2; b—轴压比为0.4。图6 径厚比的影响Fig.6 Effects of diameter-thickness ratios

4)钢渣混凝土膨胀率的影响。图7为钢渣混凝土膨胀率对试件弯矩-曲率骨架曲线的影响。试件弯矩-曲率骨架曲线在上升阶段呈线性增长,试件处于弹性阶段。随着钢渣混凝土膨胀率增加,试件弯矩-曲率骨架曲线斜率增加,屈服弯矩增加,屈服曲率无明显影响。在稳定段,随着钢渣混凝土膨胀率增加,弯矩-曲率骨架曲线斜率增加,试件抗弯承载力增加,极限曲率微增。这是因为随着钢渣混凝土膨胀率增加,钢管的约束效应增强,试件抵抗弯矩的能力增加,抗弯承载力增加。极限曲率微增是因为随着钢渣混凝土膨胀率增加,核心钢渣混凝土对钢管的侧压力增加,使得钢管也处于三向应力状态,有效防止外部钢管过早发生局部屈曲,使得延性提高,极限曲率微增。与非自应力试件相比,自应力试件的抗弯承载力提高范围是5.2%～16.8%,平均提高13.3%。

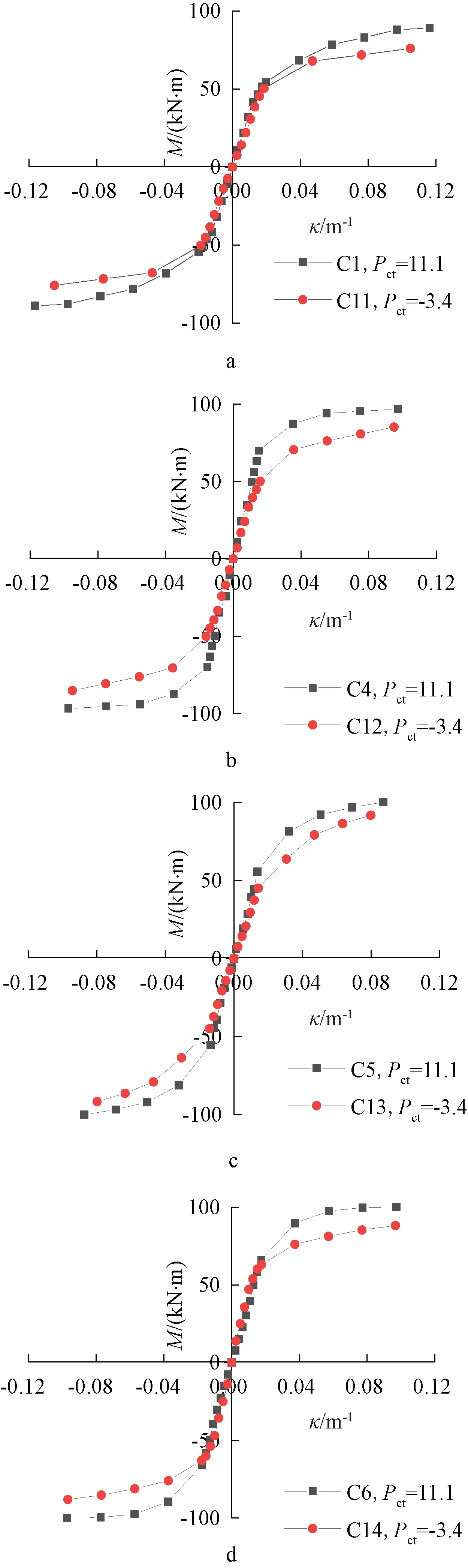
a—剪跨比为1.83; b—剪跨比为1.37; c—剪跨比为0.91; d—轴压比为0.4。图7 钢渣混凝土膨胀率的影响Fig.7 Effects of expansivity of steel slag concrete

3 数值分析

3.1 基本假定

为简化计算,作如下假定:

1)截面符合平截面假定。

2)忽略受拉区自应力钢渣混凝土的抗拉作用。

3)假设钢管与核心自应力钢渣混凝土无相对滑移。

4)不考虑剪力对试件变形影响。

5)钢管本构模型:

采用韩林海提出的钢管本构关系模型[1],其数学表达式如式(1)所示。

fyp=ψfy

(1)

式中:fyp为钢管等效强度;ψ为钢管强度利用系数;fy为钢管的屈服抗拉强度。

基于试验研究,结合文献[18]进行分析,可知:钢管强度利用率随着轴压比和钢渣混凝土膨胀率的增加而增加,随着径厚比的增加而减小。各影响因素与钢管强度利用系数大致呈线性关系。因此,通过对钢管强度利用系数进行多元线性回归分析,可得钢管强度利用系数拟合式,如式(2)所示:

ψ=0.737n+1.376η-0.000 67D/ts+

1.166

(2)

式中:η为核心钢渣混凝土自应力水平,取η=σ0/(0.67fcu),其中σ0为初始自应力,fcu为钢渣混凝土立方体抗压强度;考虑到轴压比的参数设计范围,取n=0～0.4;D/ts为钢管径厚比。

6)核心自应力钢渣混凝土本构模型:

自应力钢渣混凝土凝结硬化期间微观结构的改变力学性能较普通混凝土好,且在加载初期就已经处于三向应力状态。在韩林海提出的核心混凝土的本构模型[1]基础上,引入自应力增强系数μ[19],建立适宜于自应力钢渣混凝土的本构关系模型,其数学表达式如下。

εpo=1 300+14.93μfco+

β=(2.36×10-6)[0.25+(ξ-0.5)7](μfco)2×5×10-4

A=2-K

B=1-K

K=0.1ξ0.745

式中:σc、σpo、εc、εpo和fco分别为钢渣混凝土轴压试件应力、单轴峰值应力、压应变、单轴峰值应变和单轴抗压强度;β为数据回归分析得到的参数;μ为核心混凝土的自应力增强系数,按式μ=1+4σ0/fco计算;ξ为约束效应系数,取ξ=fyAs/(fcoAc),其中As为钢管截面积,Ac为混凝土截面积。

3.2 截面分析

全过程分析采用纤维模型法对截面应变展开分析,如图8所示。将试件的圆截面切分为若干单元,每个单元内,钢管各向同性,均匀变化。

各单元自应力钢渣混凝土应变表达式为:

εi=ε0+κy

(4)

根据式(4),可得任意单元钢管或钢渣混凝土的应力,如下所示。

σc(εc)=fc(ε0+κy)

(5a)

σs(εs)=fs(εs+κy)

(5b)

式中:σc(εc)为自应力钢渣混凝土压应力;σs(εs)为钢管的压应力。

根据截面平衡条件,得到轴力Ni表达式:

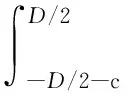
(6)

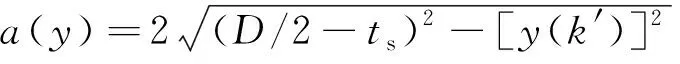
y(k′)=-D/2+Dk′×100

式中:c为中性轴与受压边缘之间的长度;a(y)、b(y)分别为截面内钢渣混凝土和钢管的积分函数;k′为划分截面的层数;y(k′)为中心轴到划分单元中心的距离。

根据截面弯矩平衡,得到弯矩Mi表达式为:

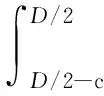
(7)

此外,考虑到附加弯矩的影响,试件水平承载力和水平位移的关系可按式(8)表达:

(8)

式中:Pi为水平承载力;H为试件有效高度;Δi为水平位移承载力。

3.3 计算程序

在截面全程分析的基础上,利用MATLAB编制非线性计算程序并进行运算,其流程如图9所示。钢管自应力钢渣混凝土柱弯矩-曲率(M-κ)骨架曲线计算步骤如下:

图9 弯矩-曲率骨架计算分析流程Fig.9 A flow chart for calculations of moment-curvature skeleton curves

1)输入基本参数H、D、N,给定最大曲率。

2)以κ0=0定义曲率的初始值,再以曲率最大值划分步长δκ=0.01,κi+1=κi+δκ。

3)定义截面形心处的应变初始值为ε0,则各单元形心处的应变为εi=ε0+yiκi。

4)确定钢材和自应力钢渣混凝土的应力σsi、σci。

5)分别由式(6)和式(7)计算内轴力Ni和内弯矩Mi。

6)如果不能满足,则对形心应变ε0进行调整,ε0=ε0+δε(δε=0.01)。

7)并重复循环步骤3)和步骤5),直至满足|Ni-Np|≤0.01,输出对应的κi和Mi。

8)然后重复布置步骤2)～7),直至计算出整个M-κ骨架曲线。

3.4 数据验证

利用上述非线性计算程序,求出试件M-κ骨架曲线计算值,将其与试验值比较,如图10所示,可以看到两者吻合较好。

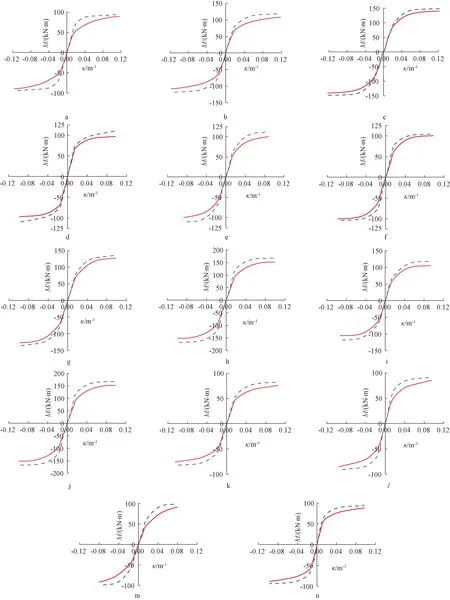
a—C1; b—C2; c—C3; d—C4; e—C5; f—C6; g—C7; h—C8; i—C9; j—C10; k—C11; l—C12; m—C13; n—C14。计算值; 试验值。图10 弯矩-曲率计算骨架曲线与试验骨架曲线对比Fig.10 Comparisons of moment-curvature calculation skeleton curves and experimental skeleton curves

3.5 参数分析

通过钢管自应力钢渣混凝土柱M-κ全过程分析,可知其影响参数主要有:轴压比、径厚比、钢渣混凝土抗压强度、钢材的屈服强度以及钢渣混凝土膨胀率等。在全过程分析结果的基础上,分析不同参数对钢管自应力钢渣混凝土柱M-κ的影响规律。

1)轴压比的影响。图11a为轴压比对钢管自应力钢渣混凝土柱M-κ关系骨架曲线的影响。可见:在较小范围内,试件抗弯承载力随着轴压比增加而增加,轴压比超过一定范围,则抗弯承载力随着轴压比增加而减小。这是因为轴压比的持续增加使得核心钢渣混凝土受到的约束效果上升,此时,试件水平位移较小,附加弯矩影响不明显,试件弹性段刚度微增。

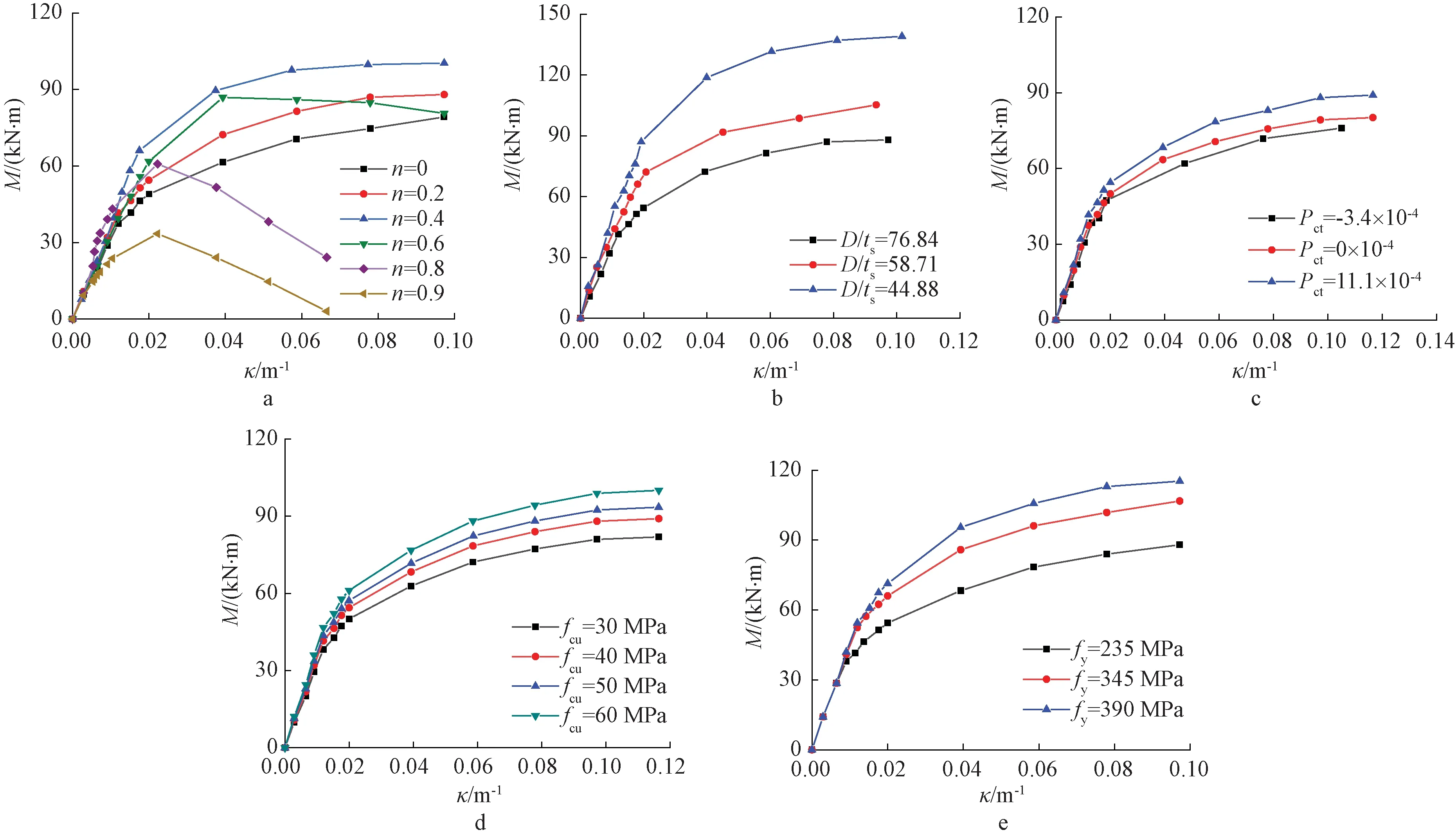
a—轴压比的影响; b—径厚比的影响; c—钢渣混凝土膨胀率的影响; d—钢渣混凝土抗压强度的影响; e—钢材屈服强度的影响。图11 参数分析示意Fig.11 Parameter analysis

2)径厚比的影响。图11b为径厚比对钢管自应力钢渣混凝土柱M-κ关系骨架曲线的影响。可见:在曲率相同时,试件抗弯承载力与径厚比整体呈负相关。这是因为径厚比的减小使得试件含钢率提高,进而提高了刚度和抗弯承载力。另一方面,随着径厚比增加,钢管对核心钢渣混凝土的约束应力提高,延迟了试件截面的破坏,进一步增加了截面抵抗弯矩的能力。

3)钢渣混凝土膨胀率的影响。图11c为钢渣混凝土膨胀率对钢管自应力钢渣混凝土柱的M-κ关系骨架曲线的影响。可见,钢渣混凝土膨胀率较高的试件,弹性阶段刚度较大,且抗弯承载能力得到提高。这是因为随着钢渣混凝土膨胀率增加,核心混凝土试件受到钢管的约束效应增强,进入三向受压状态的阶段提前,试件抗弯承载能力提高。

4)钢渣混凝土抗压强度的影响。图11d为钢渣混凝土抗压强度对钢管自应力钢渣混凝土柱的M-κ关系骨架曲线的影响。可见:核心混凝土抗压强度的提高,试件的弹性刚度及抗弯承载能力小范围增加。这是因为在钢管约束作用下,核心混凝土已经处于三向受压状态,试件整体抗弯承载能力随着钢渣混凝土抗压强度的提升而提高。

5)钢材屈服强度的影响。图11e为钢材屈服强度对钢管自应力钢渣混凝土柱的M-κ关系骨架曲线的影响。可见:提高钢管的屈服强度,试件抗弯承载力得到明显增强,而试件的弹性刚度未受到明显影响,这是因为同种钢材的弹性模量不变,弹性刚度则不受影响。

4 结束语

1)低周反复荷载作用下钢管自应力钢渣混凝土柱整体呈现压弯破坏:柱底钢管屈服后形成双向鼓曲环,且柱底的核心混凝土被压碎,产生较大塑性变形。

2)试件弯矩-曲率骨架曲线可分为上升段和稳定段。在上升阶段,随着轴压比和膨胀率的增加,曲线的斜率增大,屈服弯矩增加;随着径厚比的减小,曲线的斜率增大,屈服弯矩增加;随着剪跨比的增加,曲线的斜率降低,屈服弯矩无明显影响。在稳定阶段,随着轴压比和膨胀率的增加,曲线的斜率增大,极限弯矩增加;随着剪跨比的增加,曲线的斜率降低,极限弯矩无明显影响;随着径厚比的减小,曲线的斜率和极限弯矩无明显影响。

3)在试验研究基础上,选择合适的钢管本构模型和自应力钢渣混凝土本构模型,采用纤维模型法,编制了MATLAB非线性数值计算程序,并开展低周往复荷载作用下钢管自应力钢渣混凝土柱全过程分析,得到钢管自应力钢渣混凝土柱弯矩-曲率计算骨架曲线。计算骨架曲线与试验骨架曲线两者吻合较好。

4)参数分析结果表明:轴压比较小时,结构抗弯承载力和弹性刚度均随轴压比增加而增加,而当轴压比超过一定范围,抗弯承载力则随轴压比的增加而降低;随着钢渣混凝土膨胀率、抗压强度的增加或钢管径厚比的减小,结构的弹性刚度和抗弯承载力均得到提高;随着钢材屈服强度的增加,结构抗弯承载力提升,而弹性刚度无明显影响。