动态二元偏正态分布的尾相依函数①

王志花， 彭作祥

西南大学 数学与统计学院，重庆 400715

设(X,Y)是独立同分布的随机变量,具有连续的边缘分布函数FX,FY.对x,y≥0,定义尾相依函数为

(1)

D(1,1)为上尾相依系数[1-2].有关尾相依函数的性质见文献[3];有关尾相依系数的推导见文献[4-6].尾相依的概念描述了两个随机变量的尾相关结构,尾相关性的一个常用度量方法是所谓的尾相依系数.尾相依系数在现代风险管理中越来越受到重视,因此估计尾部依赖性是非常重要的.尾相依系数是尾相依函数的一种特殊情况,它度量两个变量之间的极值相关性.因此本文考虑动态二元偏正态分布的尾相依函数.

二元偏正态分布的联合密度函数为

f(x,y)=2φ2(x,y;ρ)Φ(α1x+α2y)α1,α2∈R

(2)

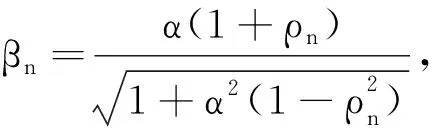
(3)

当α=0时,文献[14]给出了二元正态分布在Hüsler-Reiss条件[15]即(3)式成立情况下的尾相依函数.对x,y>0,根据(1)式再结合文献[1,14],定义(ξ,η)的下尾相依函数为

(4)

其中

(5)

本文分别考虑偏度参数α<0和α>0时的动态二元偏正态分布的尾相依函数.

1 主要结论

对参数为α∈R的偏正态分布函数F,定义

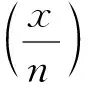
(6)

F←(x)表示F(x)的逆函数.我们有如下两个引理.

引理1设函数gn(v)由(6)式给出,则

证由文献[16]易得.

证结合引理1和(3)式得证.

定理1假设(3)式成立,则对x,y>0,有

证根据(5),(6)式以及条件概率积分公式有

(7)

其中

(8)

及(8)式可得

(9)

由(7)和(9)式,根据Φ(·)的连续性和控制收敛定理,有

由ε任意性,α<0情形得证.

(10)

根据Mills不等式

同样地

再结合引理2时(8)式取极限,有

(11)

由(7)和(11)式,根据Φ(·)的连续性和控制收敛定理,有

由ε的任意性,定理证毕.