被动调Q固体激光器非线性动力学研究

高子叶， 夏光琼， 邓涛， 林晓东，唐曦， 樊利， 吴正茂

1. 西南大学 物理科学与技术学院，重庆 400715；2. 西南大学 数学与统计学院，重庆 400715；3. 西南大学 电子信息工程学院，重庆 400715

被动调Q固体激光器具有结构紧凑、 效率高、 光束质量优异、 脉宽窄和峰值功率高等优点, 在基础科学研究、 军事、 工业加工和医疗卫生等众多领域有广泛的应用前景． 例如, 径向偏振调Q激光可用于各类金属的钻孔[1]; 高峰值功率和功率密度的调Q激光可以用于激光诱导等离子体点火[2]; 1 μm波段的调Q激光可用于治疗痤疮和黄褐斑[3]; 2.94 μm的调Q激光可消融牙本质, 从而用于牙科治疗[4]． 对于这些应用来说, 除了需要考虑调Q激光的波长范围、 偏振特性、 脉冲宽度、 脉冲能量、 脉冲峰值功率和重复频率等之外, 通常也要求调Q激光的脉冲峰值功率具有良好一致性(即脉冲峰值功率不随时间变化)． 因此, 目前关于被动调Q固体激光器的研究主要集中在激光器处于单周期振荡动力学态． 而对于被动调Q固体激光器处于其他的非线性动力学态(即脉冲峰值功率随时间变化)的研究相对较少． 在特定工作参数条件下, 被动调Q固体激光器可呈现一种特殊的非线性动力学态——脉冲混沌态, 此时其输出脉冲的峰值功率将随时间呈现复杂的混沌变化趋势． 相对于其他的混沌源而言, 基于被动调Q固体激光器产生的脉冲混沌激光具有更高的峰值功率, 将其应用到混沌雷达领域有望大幅度提高混沌雷达的作用距离． 因此, 对被动调Q固体激光器非线性动力学特性进行深入研究具有重要意义．

2003年, Tang等[5]实验观测到被动调Q Nd: YAG固体激光器表现出单周期、 倍周期以及脉冲混沌动力学态, 并从速率方程出发数值模拟了不同泵浦速率下激光器对应呈现出的3种动力学态; Wei等[6]实验观察到在不同泵浦功率下, 被动调Q Nd: YAG固体激光器呈现出单周期、 倍周期、 多周期和脉冲混沌动力学态, 且处于不同动力学态时激光横模数目不同; Ng等[7]实验观察到通过调节谐振腔, 被动调Q Nd: GdVO4和 Nd: YVO4激光器均可表现出单周期、 倍周期、 多周期和脉冲混沌动力学态; Wei等[8]实验观测到被动调Q Nd: LuVO4固体激光器也可以呈现出单周期、 倍周期和脉冲混沌动力学态, 并且处于脉冲混沌动力学态时伴随着旁瓣脉冲的出现; Yao等[9]实验观察到在较高泵浦功率下, 被动调Q Tm: YAP固体激光器输出脉冲幅度变得混乱, 认为激光器进入了脉冲混沌动力学态; Kovalsky等[10]实验证明了被动调Q Nd: YAG固态激光器输出脉冲间距具有不稳定性, 并遵循确定性低维非线性动力学规律; Du等[11]实验研究了被动调Q Tm, Ho: GdVO4固体激光器输出脉冲具有不稳定性, 并将其归因于确定性低维非线性动力学引起的; Hong等[12]理论和实验研究了被动调Q Nd: YVO4固体激光器输出激光的脉冲宽度随外部泵浦调制频率的演化路径; Bonazzola等[13-14]研究了激光横模对被动调Q固体激光器非线性动力学态的影响, 并分析了极端事件(extreme events, EEs, 极端事件定义为脉冲峰值强度高于标准偏差的4倍)出现条件; Tsai等[15]实验观测到被动调Q Nd: GdVO4偏振固体激光器呈现出单周期和脉冲混沌动力学态; Han等[16-17]实验观测到被动调Q Nd: Lu0.61Gd0.39VO4固体激光器表现出单周期和多周期动力学态． 2021年, 本课题组[18]实验观测到高重频被动调Q Nd: LaMgAl11O19固体激光器呈现出单周期和脉冲混沌动力学态, 并且分析了脉冲混沌激光的时间序列、 频谱、 相图、 自相关曲线和直方图等． 上述报道针对被动调Q固体激光器的非线性动力学态开展了部分理论和实验研究, 但是激光器的非线性动力学态随着系统关键参量(如泵浦速率、 腔内光子往返损耗、 腔内光子往返时间等)变化的演化路径还未见报道．

基于此, 本研究从四能级系统速率方程出发, 利用四阶龙格-库塔法和自适应变步长法数值研究了被动调Q Nd: YAG固体激光器的非线性动力学特性, 分析了泵浦速率、 腔内光子往返损耗、 腔内光子往返时间等关键系统参量对被动调Q Nd: YAG固体激光器非线性动力学的影响． 数值模拟结果表明: 通过选取不同的关键参量数值, 被动调Q固体激光器可呈现单周期、 倍周期、 多周期以及脉冲混沌动力学态; 连续变化其中一个关键参量的数值, 激光器的动力学态既可呈现出经历单周期、 倍周期、 多周期, 再进入脉冲混沌的演化路径; 也呈现可经历脉冲混沌、 多周期、 倍周期, 再到单周期的演化路径． 此外, 数值模拟结果呈现了处于脉冲混沌动力学态的被动调Q固体激光器出现极端事件的情形．

1 理论模型

Nd: YAG晶体具有优良的机械和光学性能, 是常用于实现脉冲宽度窄、 峰值功率高、 脉冲能量大的近红外调Q激光的固体增益介质之一[19-22]． 在近红外被动调Q固体激光器中, Cr: YAG晶体常作为可饱和吸收体使用． 因此, 本研究以Nd: YAG为激光增益介质, Cr: YAG为可饱和吸收体, Nd: YAG/Cr: YAG被动调Q固体激光器的四能级速率方程为[5]:

其中,φ为腔内光子数密度;n2,n1,n0分别为Nd: YAG的上能级粒子数密度、 下能级粒子数密度和基态粒子数密度, 并且满足n0+n1+n2=1.52×1020cm-3;ns和ns0分别为Cr: YAG的基态粒子数密度和初始粒子数密度;σe为Nd: YAG的受激发射截面;σa为Cr: YAG的吸收截面;γ21,γ20,γ10分别为Nd: YAG上能级到下能级的衰减速率、 上能级到基态的衰减速率、 下能级到基态的衰减速率;γs为Cr: YAG基态的衰减速率;lg为Nd: YAG的通光长度;ls为Cr: YAG的通光长度;c为光速;R为输出镜的反射率;L为腔内光子往返损耗;tr为腔内光子往返时间;Wp为泵浦速率． 采用四阶龙格-库塔法和自适应变步长法求解微分方程, 仿真参数见表1[5]．

表1 仿真参数

2 结果与分析

2.1 泵浦速率对被动调Q激光非线性动力学的影响

通常对于被动调Q固体激光器来说, 当增益介质和可饱和吸收体的种类和通光长度固定后, 泵浦速率、 腔内光子往返损耗、 腔内光子往返时间是影响被动调Q固体激光器非线性动力学的关键系统参量． 为了研究泵浦速率对被动调Q固体激光器非线性动力学的影响, 将腔内光子往返损耗和腔内光子往返时间固定并分别设置为0.04和800 ps． 图1和图2分别为在不同泵浦速率下, 调Q激光的时间序列和相图． 图1为时间序列, 即调Q激光的强度随时间的变化趋势图; 图2为相图, 即调Q激光的脉冲峰值功率(n+1)随脉冲峰值功率(n)的变化趋势图． 图1a和图2a是泵浦速率为600.022 500 s-1的时间序列和相图, 从时间序列图中可以看出调Q激光峰值功率具有恒定强度, 同时相图中只有一个点, 表明系统处于单周期态． 图1b和图2b是泵浦速率为600.022 550 s-1的时间序列和相图, 从时间序列图中可以看到调Q激光峰值功率具有2个数值并交替出现, 同时相图中出现了2个点, 表明系统处于倍周期态． 图1c和图2c是泵浦速率为600.022 590 s-1的时间序列和相图, 从时间序列图中可以看到调Q激光峰值功率具有4个数值并周期出现, 同时相图中出现了4个点, 表明系统处于四周期态． 图1d和图2d是泵浦速率为600.022 650 s-1的时间序列和相图, 从时间序列图中可以看到调Q激光峰值功率具有多个数值且无规律, 同时相图中出现了一条线[23], 表明系统处于脉冲混沌态．

图1 不同泵浦速率下, 被动调Q激光的时间序列

为了进一步研究激光器动力学态的演化路径, 数值模拟了调Q激光的脉冲峰值功率随泵浦速率变化的分岔图(图3)． 图3a是泵浦速率从600.022 500 s-1到600.022 700 s-1变化时, 激光器的动力学状态历经单周期、 倍周期、 多周期, 然后进入脉冲混沌态, 表明系统是经倍周期分岔路径进入脉冲混沌． 图3a中黑色虚线右侧调Q激光的脉冲峰值功率表现出无界性, 此时调Q激光部分峰值功率会出现一些较高的数值, 表明此时出现了极端事件[13]． 图3b是泵浦速率从609.100 365 s-1到609.100 455 s-1变化时, 激光器的动力学态呈现出由脉冲混沌态到单周期态的演化路径． 图3b中黑色虚线左侧部分表明调Q激光处于脉冲混沌态时也出现了极端事件．

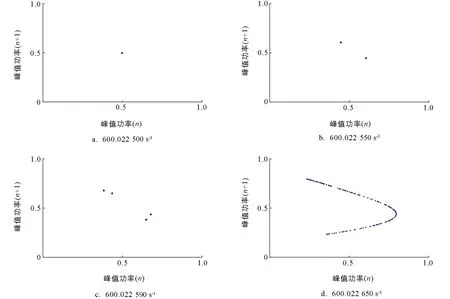
图2 不同泵浦速率下, 被动调Q激光的相图

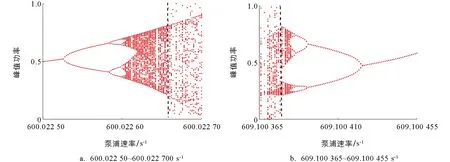
图3 调Q激光峰值功率随泵浦速率变化的分岔图

2.2 腔内光子往返损耗对被动调Q激光非线性动力学的影响

通常对于被动调Q激光器来说, 腔损耗主要包括了耦合损耗(输出镜反射率)、 随机损耗(散射、 衍射和吸收等)以及可饱和吸收体的残余吸收损耗等． 耦合损耗是输出镜引入的损耗; 随机损耗是光子在腔内往返过程中由于散射、 衍射和吸收等引入的损耗; 可饱和吸收体的残余吸收损耗主要取决于可饱和吸收体的初始透射率． 当输出镜以及可饱和吸收体的参数固定时, 通过调节谐振腔腔镜的倾角可改变随机损耗, 可以控制输出激光的非线性动力学态． 基于此, 对腔内光子往返损耗对被动调Q激光非线性动力学的影响开展了研究． 本研究中的腔内光子往返损耗(L)是指随机损耗． 为了研究腔内光子往返损耗对被动调Q激光非线性动力学的影响, 将泵浦速率和腔内光子往返时间分别设置为600 s-1和800 ps． 图4和图5分别为在不同腔内光子往返损耗下, 调Q激光的时间序列和相图． 当腔内光子往返损耗为0.048 84,0.048 86,0.048 87,0.048 88时, 调Q激光的时间序列和相图如图4a和图5a、 图4b和图5b、 图4c和图5c、 图4d和图5d所示, 表明调Q激光工作在单周期、 倍周期、 多周期和脉冲混沌态．

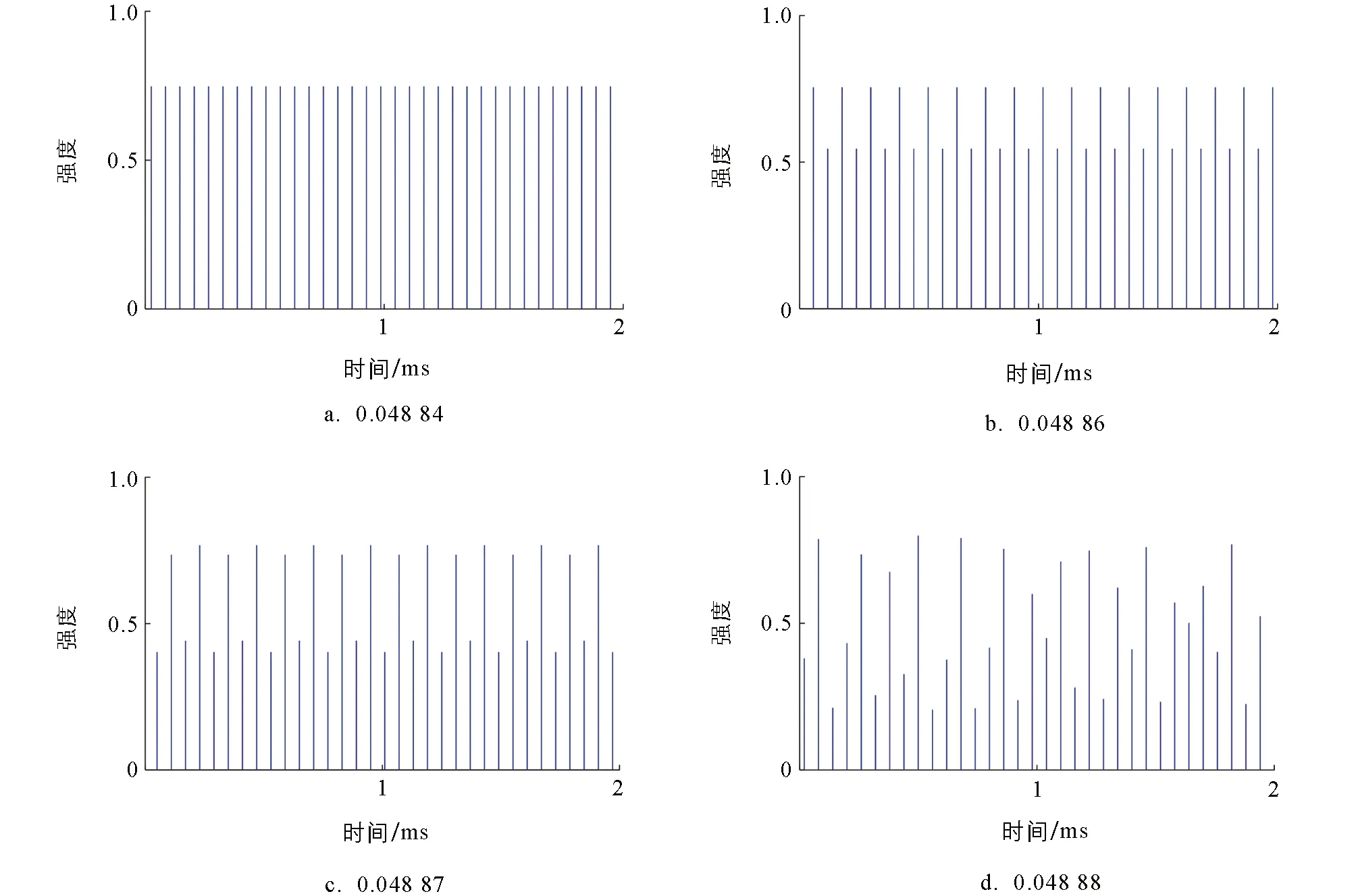
图4 在不同腔内光子往返损耗下, 被动调Q激光的时间序列

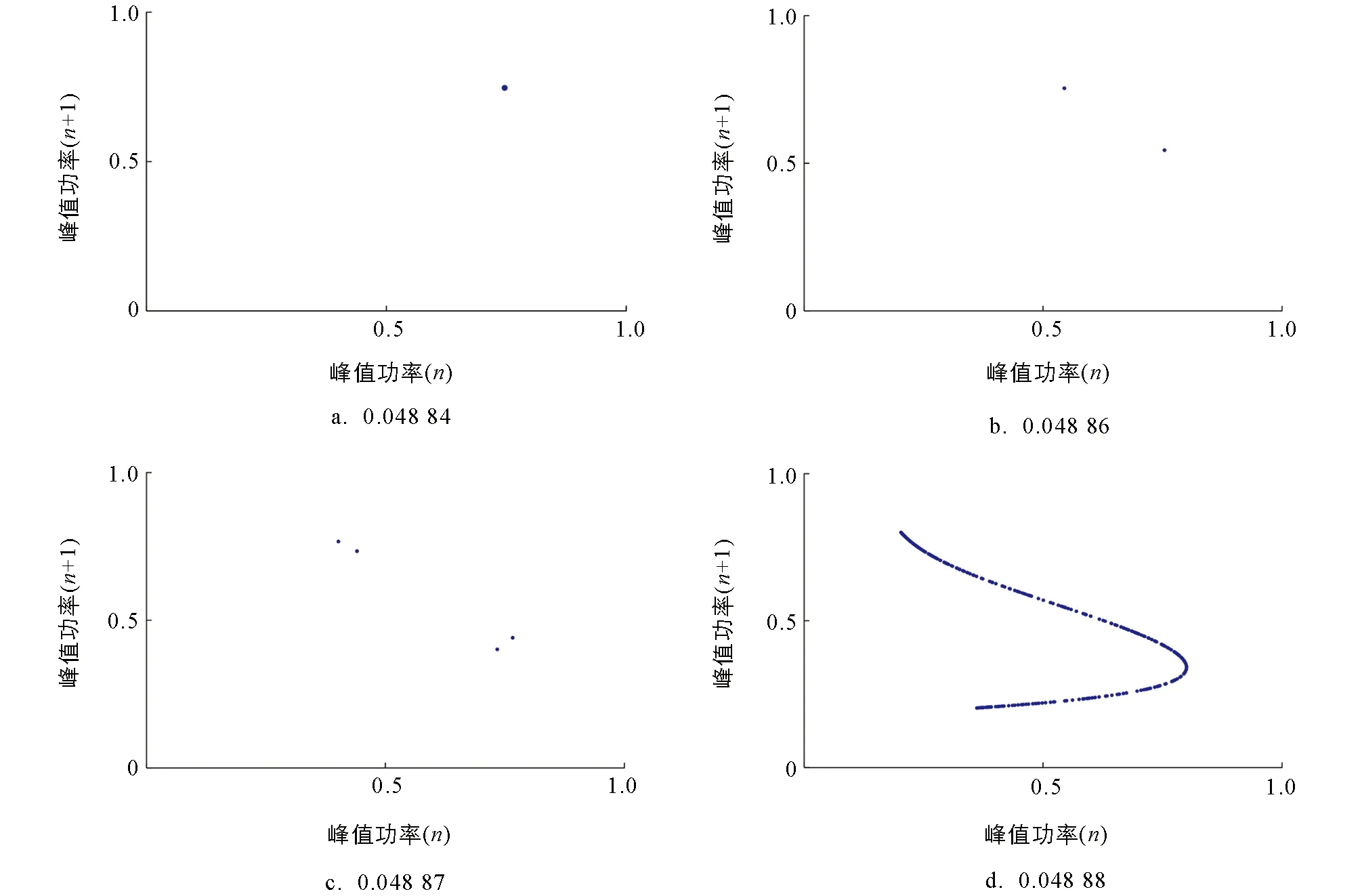
图5 在不同腔内光子往返损耗下, 被动调Q激光的相图

为了进一步分析激光器动力学状态的演化路径, 数值模拟了调Q激光峰值功率随腔内光子往返损耗变化的分岔图(图6)． 图6a是腔内光子往返损耗从0.036 43到0.036 51变化时, 激光器呈现出从脉冲混沌态到单周期态的演化路径; 图6b是腔内光子往返损耗从0.048 83到0.048 91变化时, 激光器呈现出由单周期态进入脉冲混沌态的倍周期分岔路径． 另外, 图6a和图6b中黑色虚线左侧和右侧部分也出现了极端事件．

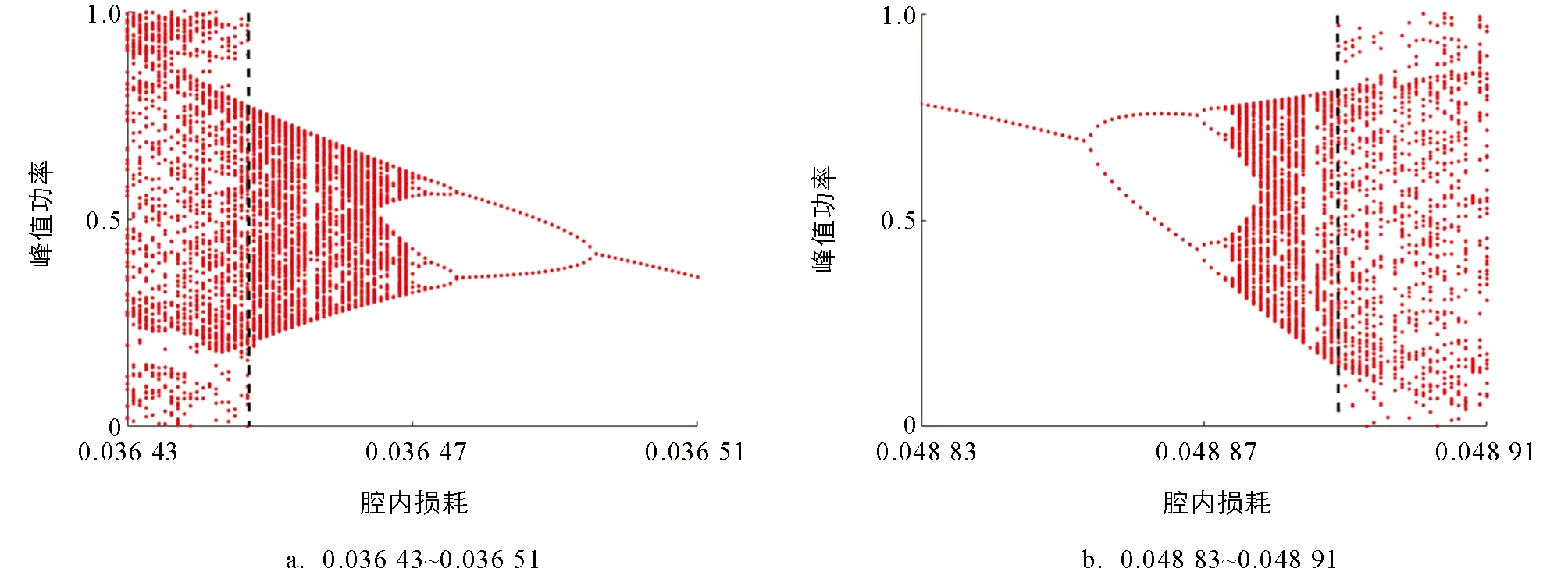
图6 调Q激光峰值功率随腔内光子往返损耗变化的分岔图

2.3 腔内光子往返时间对被动调Q激光非线性动力学的影响

对于被动调Q固体激光器来说, 增益介质、 可饱和吸收体、 谐振腔的长度共同决定了腔内光子往返时间． 当增益介质和可饱和吸收体的长度固定时, 通过调节谐振腔的长度可调节腔内光子往返时间． 为了数值模拟腔内光子往返损耗对被动调Q激光非线性动力学的影响, 将泵浦速率和腔内往返损耗分别设置为600 s-1和0.04． 图7和图8是在不同腔内光子往返时间下, 调Q激光的时间序列和相图． 当腔内光子往返时间为800.772 000,800.771 000,800.770 940,800.770 820 ps时, 调Q激光的时间序列和相图见图7和图8, 说明被动调Q激光器的动力学状态呈现为单周期、 倍周期、 多周期以及脉冲混沌态．

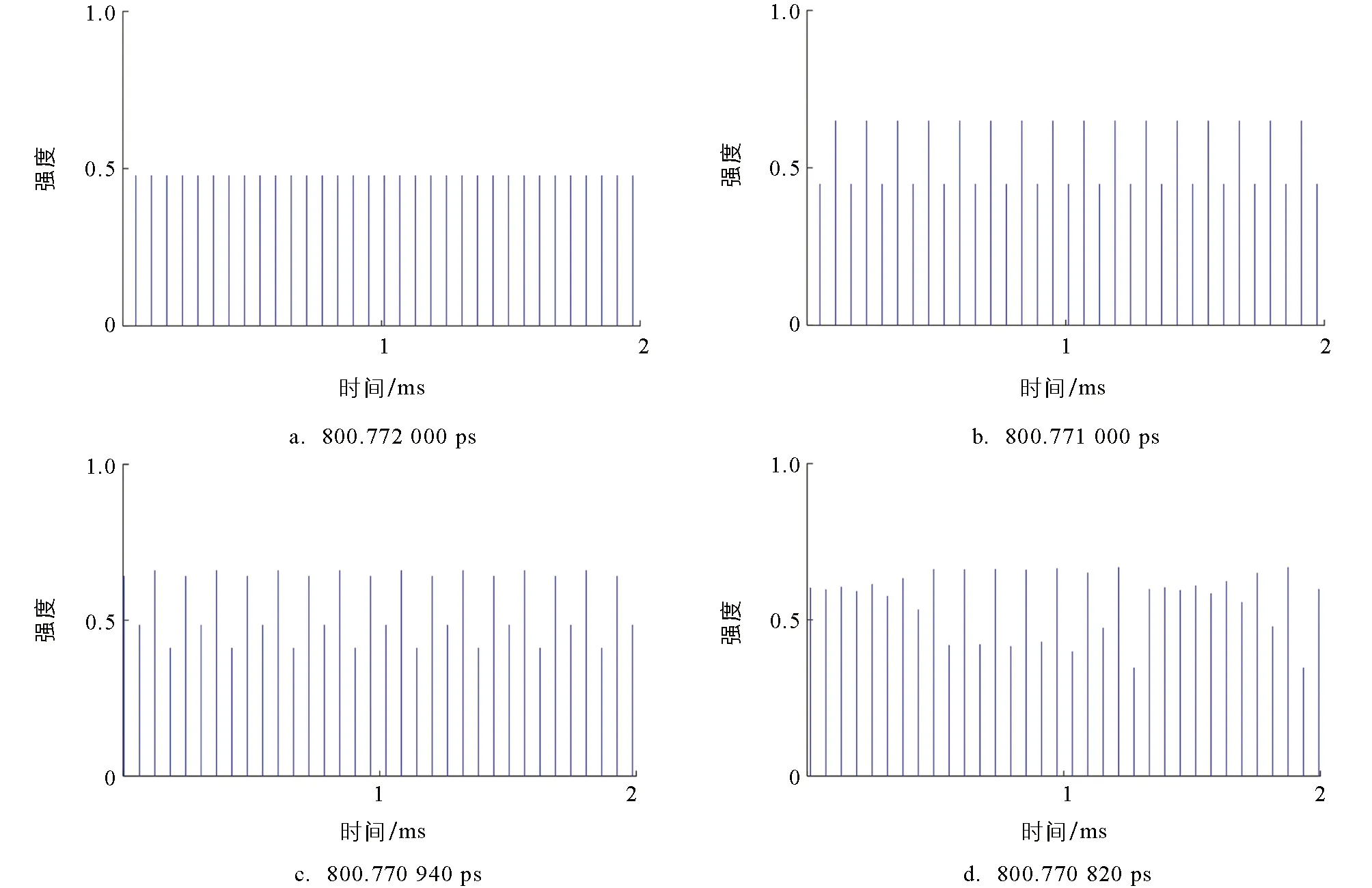
图7 不同腔内光子往返时间下, 被动调Q激光的时间序列

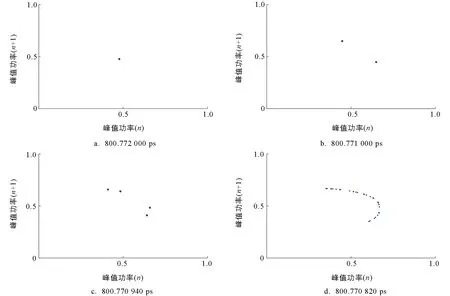
图8 不同腔内光子往返时间下, 被动调Q激光的相图

为了进一步研究腔内光子往返时间对被动调Q激光器非线性动力学的影响, 本研究数值模拟了调Q激光峰值功率随腔内光子往返时间的演化路径(图9)． 图9a和图9b是腔内光子往返时间在799.567 300～799.567 700,800.770 700～800.772 100 ps范围内, 激光器表现出单周期态进入脉冲混沌态的倍周期分岔路径以及由脉冲混沌态到单周期态的演化路径． 图9a黑色虚线右侧部分和图9b黑色虚线左侧部分表明出现了极端事件．

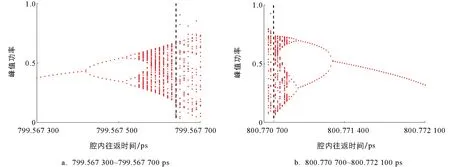
图9 调Q激光峰值功率随腔内光子往返时间变化的分岔图

3 结论

本研究基于四能级系统速率方程, 利用四阶龙格-库塔法和自适应变步长法数值模拟了被动调Q Nd: YAG固体激光器的非线性动力学特性, 分析了泵浦速率、 腔内光子往返损耗、 腔内光子往返时间等关键系统参量对被动调Q激光器非线性动力学的影响． 数值模拟结果表明: 通过选取不同的关键参量数值, 被动调Q固体激光器可工作在单周期、 倍周期、 多周期以及脉冲混沌动力学态; 当连续变化其中一个关键参量的数值, 激光器经历单周期、 倍周期、 多周期, 再进入脉冲混沌态, 呈现出倍周期分岔演化路径; 激光器也可历经脉冲混沌、 多周期、 倍周期, 再到周期态, 呈现出脉冲混沌到周期态的演化路径． 首次给出随关键系统参量变化, 被动调Q固体激光器动力学态呈现出多种演化路径． 此外, 数值模拟结果呈现了处于脉冲混沌态的被动调Q固体激光器出现极端事件的情形．