基于Apriori算法的机动车保险欺诈索赔的关联度分析

金慧　杨涵予　崔浩浩

摘 要：在保险行业中，保险欺诈是当前存在的普遍现象。然而，在保险的全部险种里面，机动车车险欺诈是保险欺诈的高发区之一。本文基于25项特征指标，应用车险欺诈关联分析模型对某保险公司欺诈识别系统数据进行了分析，得出黑色样本的频繁项集，并且在白色样本中进行验证，确定了它们之间的具体关联规则，识别出欺诈索赔事件，得到灰色样本的欺诈率。研究结果表明，总理赔样本的欺诈率为37.527%。

关键词：车险欺诈 关联分析 Apriori算法 欺诈率

1 引言

2019年6月中国保险学会与金融壹账通联合发布了《2019年中国保险行业智能风控白皮书》，文中说明就目前我国的所有保险行业里面，车险欺诈渗透约占理赔金额比例高达20%，相应的年损失竟有200多亿元，可谓是触目惊心[5]。在近几年来，我国车险行业发展迅速，然而当前车险欺诈一直伴随着汽车保险的发展，高速的发展带来的结果是保险的经营成本一直在增加，随着当前欺诈手段和欺诈形式的多样化，其车险欺诈分别给保险公司、合法投保人以及车险行业的稳定发展带来了极大的危害[1]。为确保保险行业健康并且相对稳定的发展，减少一些大众化的保险欺诈，维护一些诚实投保人的利益，保险反欺诈技术研究具有一定的现实意义[4]。

2 建立Apriori算法模型

Apriori算法有两个重要性质。性质1，频繁项集的一切子集则均为频繁项集；性质2，非频繁集项的超集则必然为非频繁的[2]。

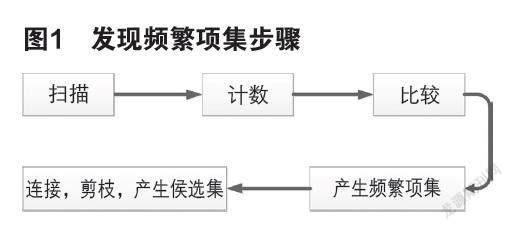
可以将其整个发现频繁项集的过程简述见图1。首先，我们将频繁项集中的“1项集”所有的集合寻找出来，标号为L1，在此“1项集”的基础上，找出频繁项集中的“2项集”，标号为L2，同样的道理，依次找出文中所需的频繁项集的其他项集；但其间，每一次寻找项集时都必须扫描一次数据库。核心是连接步以及剪枝步两个内容；连接步就是将其自行连接，但前提条件是前面的“K2”项必须要相同，它们按照26个英文字母的顺序依次连接；剪枝步的目的是让其随便一项频繁项集的一切非空子集都必须遵循频繁的原则[3，6]。

重复上述5个步骤，一直到频繁项集不出现时即可结束。

3 车险欺诈关联分析及欺诈率估计

3.1 数据的收集和数据的处理

将国内某保险公司某年的59627例索赔样本由保险公司内部的理赔管理系统做出初步的筛选；其中将所有的车险理赔样本分为两类，高风险子集样本（欺诈样本）和低风险子集样本（合理索赔样本）。表1为具体的数据量。

在表1中将索赔样本占有量做出具体分组，本公司针对是否为车险欺诈一共利用25个特征指标（如表2所示）对其所有理赔样本进行识别，最终识别是否为欺诈索赔，其中任何一项特征指标都针对某一方面车险欺诈与正常索赔的具体特征的差异[7-8]。

通过以下的步骤对将样本进行分类。

（1）将高风险的子集进行排序并从中筛选出高嫌疑和占比与高风险的子集欺诈率相等的欺诈样本的一部分；（2）对样本所有数据进行排序，接着筛选出占比和总样本的欺诈率相同的欺诈样本；（3）将上述1与2做交集，将得到文中所需要的黑色样本数量；（4）低风险子集按照需要排序将其中的没有嫌疑与占比（1-低风险的欺诈率）相等的样本筛选出来；（5）总样本按照所需排序将其中占比与（1-总样本的欺诈率）相等的样本筛选出来；（6）将上述的4与5做交集，将得到文中所需要的白色样本的数量。用总样本数量减去黑色样本数量和白色样本数量将得到灰色样本数量。最后得出的各类样本数量如表3所示。

3.2 欺诈模式与非欺诈模式两者区别

3.2.1 欺诈样本的频繁项集

最初，我们需要找出频繁项集（此处频繁项集指的是欺诈样本与非欺诈样本两者的具体频繁项集）。25项特征指标记为i，如果满足，则i=1，如果不满足，则i=0。

在本文的研究中将最小的支持度以及最小置信度分别预设为0.3与0.7，也就是说当同时满足两个条件，一最小支持度>0.3；二最小置信度>0.7。接着对二、三、四项集进行同样的分析。在欺诈样本的二频繁项集中，0.8323为二项频繁项集里面的最高支持度，对应的二项集为{19，20}，这也说明当两个指标同一时间同时出西现时，有80%的把握可以认定此样本为欺诈样本，表中的频繁项集{10，20}，{10，19}，{20，5}同样认为是较高的支持度，对应支持度是0.77，0.64，0.64。

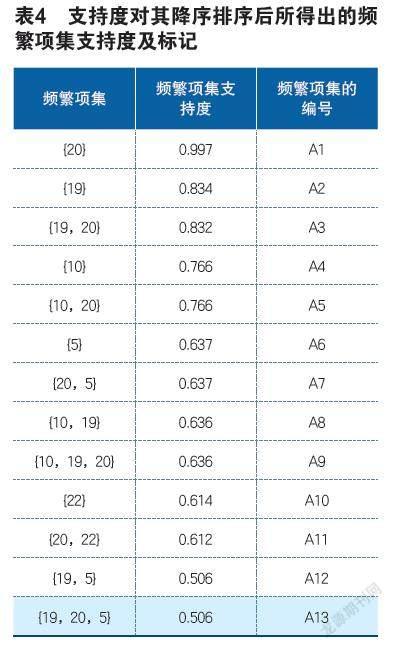
将上述的13项频繁项集算出的支持度依次排序，顺序按降序排列，如下表4所示，将其对应的支持度做出适当的调整，为后面的频繁项集用于灰色样本的一些预测做铺垫。

3.2.2 非欺诈样本的频繁项集

在表4里面结果可以显示，将其最小支持度具体设为0.5的时候，可以得出其中的13项是频繁项集，然而非欺诈样本与欺诈样本存在着明显的差异；将其最小支持度设为0.4的时候，仅包含其中的两项频繁项集为非欺诈的样本，它们为项集{5}和项集{10}，得出的结果均在正常的范围之内，因为指标选择它们都指向欺诈。

3.3 关联规则的分析

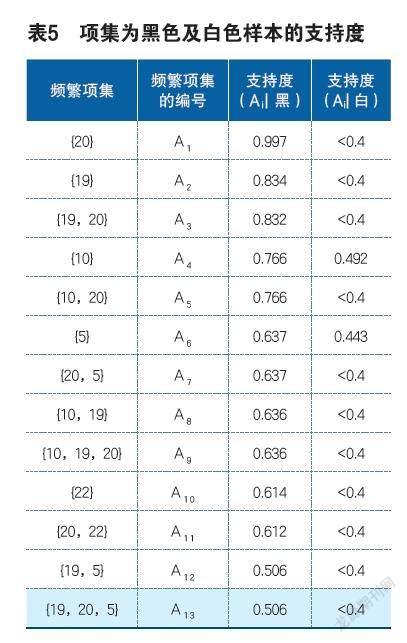
在挖掘关联规则时应该注意它们的有效性，对前文筛选后所得到的13项黑色样本的频繁项集在白色样本里面都要进行具体的验证，看是否是有效的，在验证之前需要将前文的13个频繁项集分别做出标记，方便進行操作，如表4所示。

验证频繁项集是否为有效的，需要满足以下条件：

黑色样本是基础，对于Ai的支持度有一定的满足条件见式1，假如满足，则视为有效。

支持度（Ai黑）>支持度（Ai白）（1）

得出结果如表5所示，其上述的13个频繁项集均为有效的。

接下来需要将各个项集之间的关联规则挖掘出来。随便一项以频繁项集为基础的黑色样本的概率均可以由贝叶斯公式计算得出，运用式2得出所有频繁项集下对应的欺诈率。

P（黑|Ai）=

（2）

将P（F|Ai）记作P1，2，3，……，13。

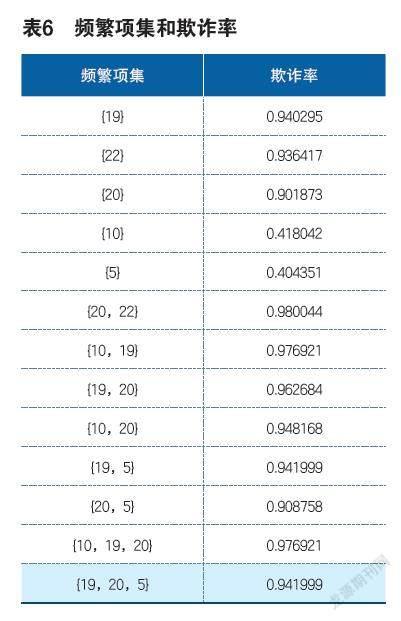
频繁项集以及欺诈率将通过表6列举出来。

由上述的欺诈率可以将每个频繁项集的关联规则全部找出，将高欺诈率频繁项集{19}，{22}，{10}，{5}等4个项集的相关的关联规则分别做出列举。

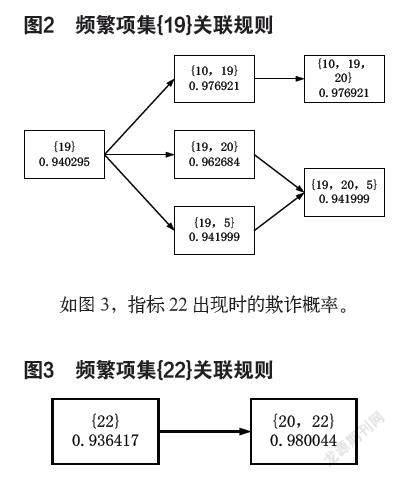
如图2所示，指标19出现时，欺诈率为0.940295，当指标10与19同时出现，欺诈率为0.976921，还有当指标19与20同时出现时，欺诈率变为0.962684（指标19与指标5同时出现时欺诈率变为0.941999），

如指标10、19、20出现，索赔中含有欺诈的概率为97.69%；指标19、20、5出现，此时索赔中含有的欺诈概率为94.19%。

如图3，指标22出现时的欺诈概率。

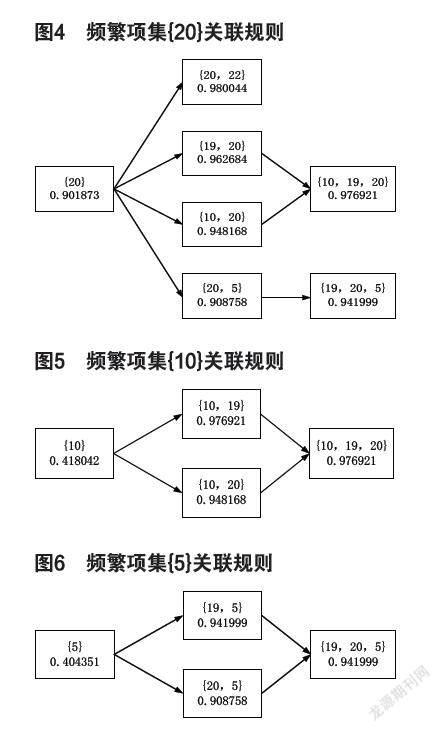
如图4，指标20出现时的欺诈率。

如图5，指标10出现时的欺诈率。

如图6，指标5出现时的欺诈率。

4 欺诈识别

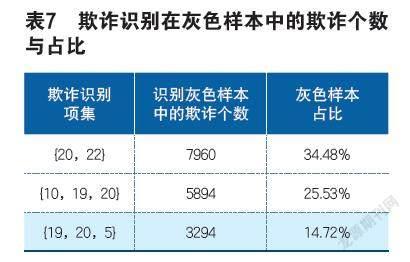
上文中得出的显著关联规则有三个，最终结果显示为项集{20，22}，项集{10，19，20}和项集{19，20，5}，它们对应的欺诈率分别为98.00%，97.69%和94.20%。因此，用上述的三个项集用作欺诈识别。灰色样本的具体占比识别详见表7。

4.1 样本预测

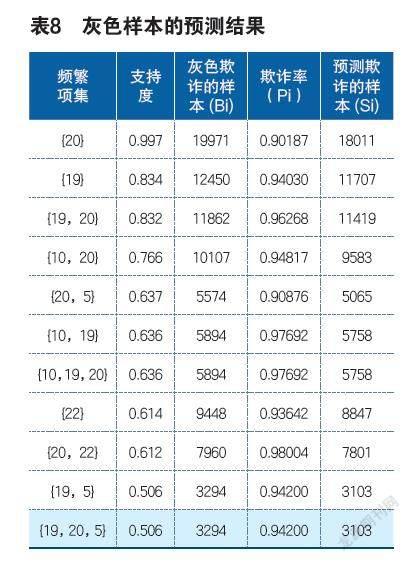
在标记的13项频繁项集里面，只有满足条件P（黑|Ai）>0.8时，才能将其作为预测对象，最后符合条件的较为显著的频繁项集共计11项，将支持度从0.5调升至0.8，将置信度由0.85提升至0.95，再分别做出预测观察结果。预测结果如表9所示。

表8中的欺诈率计算见式3。

pi=P（F|Ai） （3）

4.2 估计灰色样本的欺诈率

根据从B1至B13有无交集，将对灰色的样本欺诈率进行估计分为两种情况。

第一种情况，假如B1至B13没有交集，则可用公式4将总的欺诈率算出来。

（4）

其中，X=23085为灰色样本的总数

第二种情况，假如B1至B13有交集。将P1至P13的大小进行比较，用科学的方法，将交集的部分分到概率大的集合中，假如只有四个频繁项集并且满足P1>P2>P3>P4。

因为B1+B2+B3+B4+B5+B6+B7+B8+B9+B10+B11+B12+B13相加之和远远大于23085，所有样本之间存在着交集，因此运用第二种情况来计算。由前文的表格中可以得出：

P（F|A11）>P（F|A9）≥P（F|A8）>P（F|A3）>P（F|A5）>P（F|A13）≥P（F|A12）>P（F|A2）>P（F|A10）>P（F|A7）>P（F|A1）

上面所述的13项的频繁项集的区分度都是一致的。而且将它们的全部支持度都按照大小进行相关顺序排列，假如它们的支持度与区分度的大小两者之间是相同的，就要用它们频繁项集的具体个数将其进行排列顺序；灰色样本的欺诈率计算大致为三步。

（1）首先将排序后的第一个B11与（B9，B8，B3，B5，B13，B12，B2，B10，B7，B1）做交集，其交集的结果属于B11，然后计算，S11=B11*P（F|A11）；

（2）去掉计算过的B11，将B9与剩下的几项（B8，B3，B5，B13，B12，B2，B10，B7，B1）做交集，同样交集的结果属于B9，接着计算，S9=B9*P（F|A9）；

（3）循环1和2步骤，计算到所有的样本没有交集为止。最后用公式4计算出灰色样本的欺诈率：

（5）

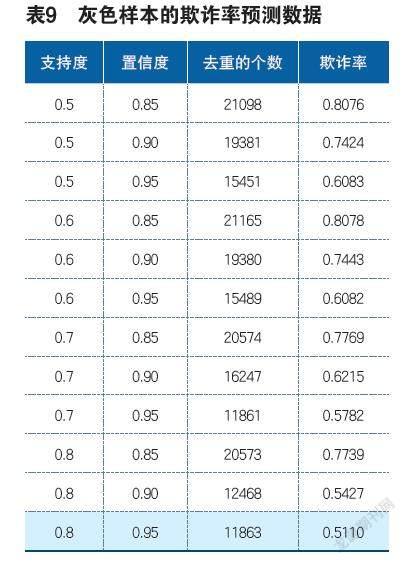
调整支持度与置信度，由小向大调，从而预测灰色样本的最终欺诈率见表9；其取值越大，那么结果也就也接近真实数据，得出灰色样本的具体欺诈率达到51.1%时，对应它们的支持度与区分度两个数据分别为0.8与0.95。

由此可以得出，灰色样本的欺诈率为0.5110，灰色样本中的欺诈个数为（23085*0.5110）11796个，黑色样本为10580个，最终的欺诈样本个数（10580+11796）为22376个；结果得出的总体欺诈率为：

5 结语

本文以国内某保险公司车险理赔数据进行关联规则分析，运用相关的25项特征指标将所有具有明显欺诈行为特征的频繁项集全部挖掘出来，最终用于欺诈索赔的识别。

（1）本文基于Apriori算法，对保险公司已知的黑色样本做出关联分析，运用算法得出研究所需的13项频繁项集，接着在白色样本中对比验证，结果发现均有效，将所有频繁项集各项之间的关联规则进行具体的挖掘，用于灰色样本部分的欺诈识别。结果显示，当项集{20，22}、{10，19，20}和{19，20，5}分别出现时，识别的欺诈个数分别为7960、5894和3294，对应的灰色样本占比分别为34.48%、25.53%和14.72%，灰色样本预测欺诈结果显示，在不确定的索赔样本中约有50%的样本为欺诈样本。

（2）灰色样本最终得出的欺诈率预计结果将直接受到频繁项集支持度的影响，随支持度的升高，其预计结果越接近真实的数据，文中将支持度与置信度做出调整（支持度由0.5调至0.8，置信度由0.85调至0.95）后得出灰色样本欺诈率的预测结果是0.5110，此时计算出的总理赔样本的欺诈率为37.527%；保监局公布的一些调查数据中显示，国内的车险欺诈索赔金额占据整个车险索赔金额的30%之多，所以符合车险欺诈的预测范围。

基金项目：甘肃省教育厅创新能力提升项目（2021B-315）。

参考文献：

[1]何奇龙，唐煦韩，唐娟红.基于演化博弈的机动车保险欺诈问题研究[J].保险职业学院学报，2022，36（02）：51-59.

[2]张辉. 基于改进Apriori算法的典型民航不安全事件影响因素关联分析[D].中国民用航空飞行学院，2022.

[3]张硕. 基于数据挖掘的告警关联规则研究与设计[D].贵州大学，2021.

[4]車险反欺诈联合课题组.车险欺诈与反欺诈问题研究及监管建议[J].保险研究，2021（06）：3-10.

[5]陈秀娟.国内车险欺诈渗漏率达20％[J]. 汽车观察，2019（7）：1.

[6]杨洋.机动车辆保险欺诈风险评估模型构建及其应用研究[D].重庆理工大学，2022.

[7]卢冰洁，李炜卓，那崇宁，牛作尧，陈奎.机器学习模型在车险欺诈检测的研究进展[J].计算机工程与应用，2022，58（05）：34-49.

[8]楚宵莹.基于机器学习的机动车辆保险的欺诈识别研究[D].山东大学，2021.