一类综合控制系统的动态输出反馈H∞控制器设计

孙 凤 琪

(吉林师范大学 数学与计算机学院,吉林 四平 136000)

控制理论在数学、计算机科学以及工程学等领域应用广泛[1-3].在控制系统中,输出测量只能局部反应受控系统信息而不能全局实施系统镇定,从而影响实际控制效果,利用静态和动态输出反馈H∞控制可有效解决该问题,对时滞、奇异摄动和不确定性综合存在的系统性输出反馈H∞控制器设计已引起人们广泛关注[4-5].输出反馈H∞控制是在H∞空间通过某些性能指标的无穷范数优化而获得控制器的一种控制方法,广泛应用于控制工程等领域[6-8].文献[7-9]设计了带有记忆的动态输出反馈H∞控制器以及新的切换规则,为不确定多时滞线性切换系统的理论研究提供了更多可能性,但未考虑奇异摄动性; 文献[10-11]设计了状态反馈非脆弱H∞控制器,设计方法复杂,该方法需引入较多的矩阵变量,使计算量较大,推理过程繁琐,且未引入矩阵工具箱手段,不便于实际应用; 文献[12-13]研究了广义系统以及时变时滞状态下的动态输出反馈H∞控制器设计问题,但仅针对时滞控制系统,所得的结果受限.

本文在此基础上,对具有奇异摄动、不确定性和时变时滞的综合控制系统进行输出反馈H∞控制器设计,运用Lyapunov稳定性理论和矩阵分析理论,选取适当的交叉项界定法,推出满足H∞性能指标的动态输出反馈H∞控制器设计新方法,所得结果具有较低的保守性.最后用数值算例验证结论的可行性.

1 无记忆动态输出反馈H∞控制器设计

考虑如下具有控制输入和干扰输入的不确定性时变时滞奇异摄动控制系统

(1)

(2)

τ,μ为已知的实常数,F(t)∈i×j为具有Lebesgue可测元的适当维数的不确定矩阵,其不确定性满足范数有界条件

FTF≤I.

(3)

设计无记忆动态输出反馈H∞控制器

(4)

其中xk∈nk为控制器状态,nk为控制器阶数,r≤nk≤n,K1,K2,K3,K4为待确定控制器的参数矩阵,则闭环系统为

(5)

其中M1=A+DF(t)E1+B1K4C2,M2=Ad+DF(t)Ed,M3=C1+B2K4C2.

下面在时滞依赖情形下,设计无记忆动态输出反馈H∞控制器(4),即对给定的性能指标γ>0,若闭环系统(5)满足如下条件:

1) 当w(t)=0时,系统是渐近稳定的;

2) 在零初始条件下,∀w(t)∈L2[0,∞)从外部干扰w(t)到被调输出z(t)传递函数的H∞范数满足Gzw(s)<γ,即‖z(t)‖2<γ‖w(t)‖2,则系统(1)是渐近稳定的,且满足给定的H∞性能指标.

本文所有定理均在满足文献[14]的引理2.1条件下成立.

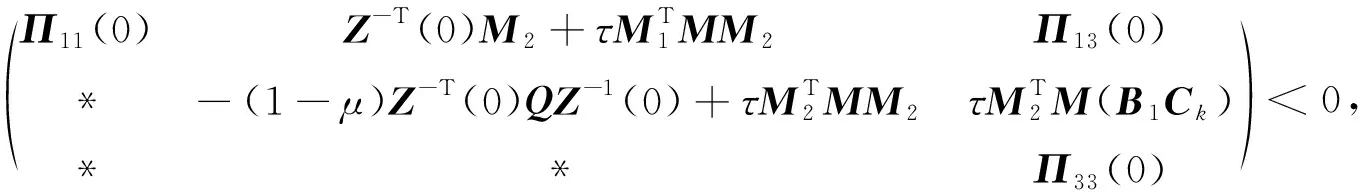
(6)

(7)

(8)

(9)

其中

证明: 不妨假设w(t)=0,构造新的依赖控制器状态的Lyapunov-Krasovskii(L-K)泛函

V(x(t))=V1(x(t))+V2(x(t))+V3(x(t))+V4(x(t)),

其中

Q,M,H为待定适当维数的正定对称矩阵,则V(x(t))>0.

将V(x(t))沿系统(1)的任意轨迹进行微分,由文献[14]引理2.5可知,存在适当维数的矩阵P,对称阵N和R,使得

由于

其中

当w(t)≠0时,同理可证

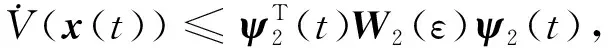
其中

其中

故

其中

(10)

矩阵不等式(10)<0关于未知变量γ,Ak,Bk,Ck,Dk,H,Q,M,N,P,R和Z(ε)是非线性的,进行线性化处理后,可得如下线性化定理.

其中

Ω11(0)=ZT(0)AT+(B1K4)T+AZ(0)+B1K4+Q-N+ηDDT,

Ω15(0)=ZT(0)AT+(B1K4)T+ηDDT,

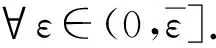
注1定理2是在构造新的Lyapunov泛函基础上进行研究的,考虑的系统是综合控制系统,可采用不同的交叉项界定,进而推出更优越的稳定性判据.

2 记忆动态输出反馈H∞控制器设计

对系统(1),设计记忆动态输出反馈H∞控制器为

其中xk∈nk为控制器状态,nk为控制器阶数,r≤nk≤n,Ak,Bk,Ck1,Ck2,Dk1,Dk2为待确定控制器的参数矩阵,则闭环系统变为

(11)

其中M1=A+DF(t)E1+B1Dk1C2,M2=Ad+DF(t)Ed+B1Dk2C2,M3=C1+B2Dk1C2.

其中

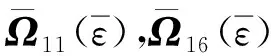
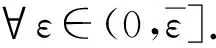
类似于定理2的证明过程,故略.

3 算 例

考虑文献[15]中的数值算例

其中

取H∞性能指标γ=1.1,小于文献[15]中的H∞性能指标γ=1.561 7.为与文献进行对比,考虑系统不含输出的情形.在奇异摄动系统(1)中,令

对于时滞,假设其满足

Z1=0.326 9,Z2=0.223 7,Z3=0.014 7,Z4=0.005 9,Z5=-0.038 8,η=0.172 4,

综上,本文对具有时变时滞、鲁棒性和奇异摄动的综合控制系统进行输出反馈H∞控制器设计,在构造含有摄动相关的L-K泛函基础上,设计了新的无记忆和记忆动态输出反馈H∞控制器.通过对比现有文献,所得的结果具有较低的保守性[15-17],适用于标准和非标准情形,可为H2/H∞控制、H∞滤波以及电力系统等领域的控制问题提供理论参考[18-20].