连续时间Guichardet-Fock空间中的Dirichlet形式

李晓慧,周玉兰,房彦兵,张 银

(1.宁夏大学 前沿交叉学院,宁夏 中卫 755099; 2.西北师范大学 数学与统计学院,兰州 730070; 3.吉利学院 智能科技学院,成都 641402)

0 引 言

量子随机分析理论[1]是经典It随机积分理论中的一种非交换扩张,是一种算子随机积分理论[2].量子随机积分在Fock空间中可描述具有增生、湮灭等性质的物理系统,因此其在物理和工程等领域应用广泛[2-3].Guichardet-Fock空间是量子领域的基本概念,主要用于量子随机积分问题中,Guichardet-Fock空间不仅与经典It随机积分理论的Fock空间在线性运算上同构,而且比其空间结构更丰富[4].因此,研究Guichardet-Fock空间上的相关性质有一定的理论意义.

Dirichlet形式在概率理论、量子随机积分理论和随机动力学中应用广泛.文献[5]利用白噪声框架(Hida可导算子)介绍了无穷维空间中的Dirichlet形式及性质; 文献[6]研究了非对称随机积分,将零连续可加性泛函随机积分从对称的Dirichlet形式推广到非对称形式; 文献[7-11]在不同空间中讨论了Dirichlet形式的性质及应用; 文献[12]将对称卷积半群与满足平移性的非交换Dirichlet形式之间确定了一对一关系,从而为一些半群的研究提供了有利工具.

文献[13]讨论了连续时间Guichardet-Fock空间L2(Γ;η)中广义算子的Mallivin变分理论,证明了空间中的算子在极大定义域条件下可突破指数域的限制,实现算子之间的复合; 文献[14]在L2(Γ;η)中将文献[13]中的随机梯度及点态随机梯度s进行了修正,使修正后的算子具有真正湮灭、增生的物理意义; 文献[15]在L2(Γ;η)中将文献[14]中的修正随机梯度与Skorohod积分进行了推广,即算子和积分的广义化,并给出了广义修正随机梯度与广义Skorohod积分之间的关系; 文献[16]讨论了L2(Γ;η)中计数算子N的性质及其表示; 文献[17]在L2(Γ;η)中将文献[16]的计数算子进行了推广,即广义计数算子,并给出了其Skorohod积分-随机梯度表示.基于上述研究结果,本文在L2(Γ;η)中首先定义加权计数算子Sω和双线性型算子

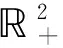
1 预备知识

Γ={σ⊂+|#σ<∞},

其中#σ表示集合σ的基数.对∀n≥1,Γ(n)表示Γ中有n个元素子集的集合,表示为

特别地,Γ(0)={Ø}为Γ中测度为1的原子,对∀n≥1,Γ(n)中测度为+上的对称Lebesgue测度,是+n中测度λn的对称化,即为方便,将Γ中的元素用α,β,σ,τ等表示.

设η是复Hilbert空间,其上内积和范数分别记作〈·,·〉η和|·|η,L2(Γ;η)是Γ上η值平方可积函数构成的Hilbert空间.约定L2(Γ;η)上的范数为‖·‖,内积为

定义1[4]对∀s,t∈+及∀σ,τ∈Γ,定义表示τ的示性函数.

定义2[14]对∀(τ,s)∈Γ×+,设L2(Γ;η)中修正随机梯度是稠定无界算子,定义为

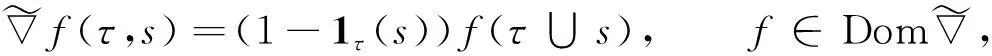
(1)

这里

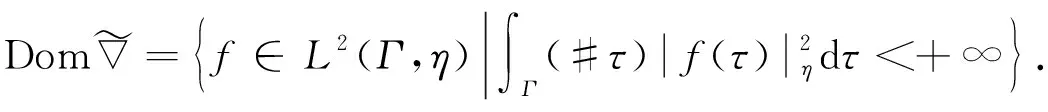
(2)

定义3[14]对∀s∈+及∀τ∈Γ,L2(Γ;η)中的点态修正随机梯度定义为

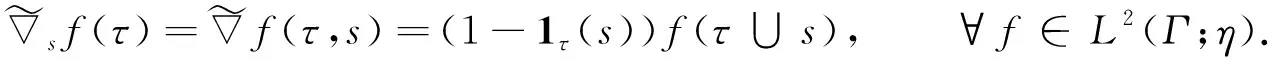
(3)

其共轭算子为

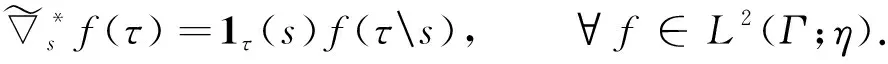
(4)

引理1[14]对∀s∈+,L2(Γ;η)中的点态修正随机梯度及其共轭为有界线性算子,且

定义4[16]连续时间Guichardet-Fock空间L2(Γ;η)中的计数算子N定义为

Nf(σ)=#σf(σ), ∀f∈DomN,

(5)

其中

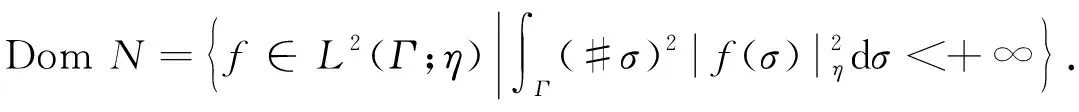
(6)

引理2[16]L2(Γ;η)中的计数算子N是稠定、无界、自伴的闭线性算子,且有如下3种表示形式:

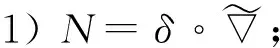
其中δ是L2(Γ;η)中的Skorohod积分,Jn是L2(Γ;η)到L2(Γ(n);η)的正交投影.

定义5[12]设X是Banach空间,若有界算子族(Tt)t≥0满足:

1)T(0)=U;

2)T(t+s)=T(s)T(t),∀t,s≥0;

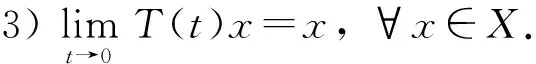
则称(Tt)t≥0为C0-半群,其中U是单位算子.

定义6[8]若函数C:→满足:

1)C(0)=0;

2) |C(s)-C(t)|≤|s-t|,∀s,t∈.

则称函数C为压缩函数.

引理3[9]若C为压缩函数,则∀ξ∈S,C∘ξ∈S,其中S是L2(Γ;η)中的闭子空间.

引理4[8]一个正的、对称的、稠密的且满足压缩性质的Hilbert空间为Dirichlet形式.

2 主要结果

首先,定义L2(Γ;η)中的加权计数算子Sω及双线性算子ε(f,g).其次,证明L2(Γ;η)中的“energy”形式(ε,Domε)是Dirichlet形式.最后,讨论(ε,Domε)与加权计数算子Sω及C0-半群(Tt)t≥0=(e-tSω)t≥0的关系:

1)ε(f,g)=〈〈f,Sωg〉〉,∀f∈Domε,∀g∈DomSω;

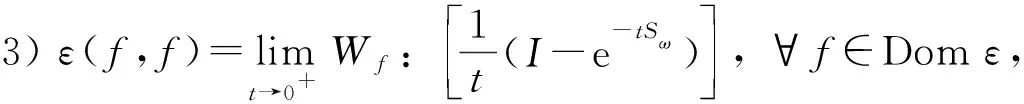
则νω(σ)称为Γ上关于ω(s,t)的计数函数.

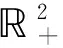
Sωf(σ)=νω(σ)f(σ),f∈DomSω,

(7)

这里

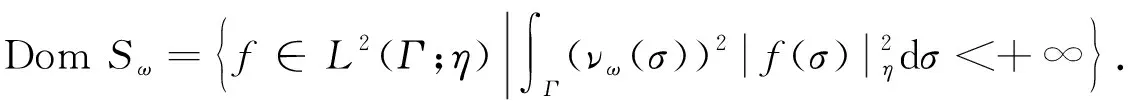
(8)

定义9设h是+上的非负实函数,L2(Γ;η)的一维加权计数算子,表示为

Nhf(σ)=#h(σ)f(σ),f∈DomNh,

(9)

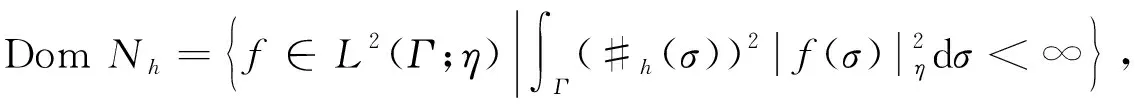
(10)

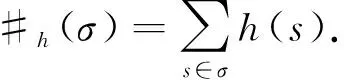
注2对∀s∈+,定义+上的非负实函数ω(·,t):tω(s,t),则Nω(·,t)为L2(Γ;η)的一维加权计数算子; 对∀t∈+,定义+上的非负实函数ω(s,·):sω(s,t),则Nω(s,·)为L2(Γ;η)的一维加权计数算子.

注3一维加权计数算子和二维加权计数算子统称为加权计数算子.

下面定义双线性算子ε,并证明“energy”形式(ε,Domε)为Dirichlet形式.

定理1定义L2(Γ;η)的线性子空间为

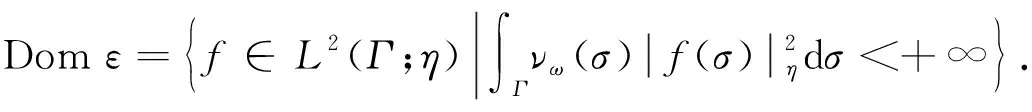
(11)

则Domε是L2(Γ;η)的稠密线性子空间,且对∀f,g∈Domε,积分

(12)

存在且绝对收敛.

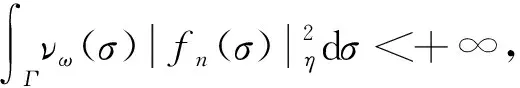
于是

即f∈Domε,因此Domε是闭的.因为Domε⊂L2(Γ;η),故Domε是L2(Γ;η)的稠密线性子空间.

下面证明积分式(12)存在且绝对收敛.对∀f,g∈Domε及∀s,t∈+,有

同理

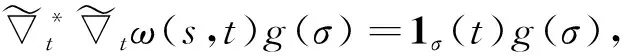
则

由Cauchy-Schwartz不等式可得

定义10对∀f,g∈Domε,定义L2(Γ;η)中的双线性型算子ε为

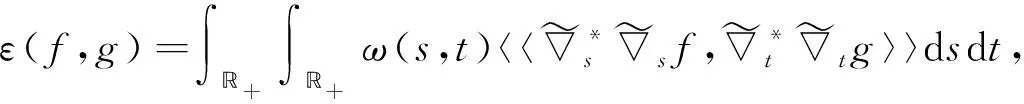
(13)

且(ε,Domε)称为“energy”形式.

注41) (ε,Domε)是一个正的、对称的且稠密的Hilbert空间;

2) 对∀f∈ Domε,有

定理2(ε,Domε)是L2(Γ;η)中的Dirichlet形式.

证明: 首先证明(ε,Domε)满足压缩性质.设C:→是压缩函数,对∀f∈Domε,由引理3可得|C∘f|η≤|f(σ)|η,则

因此C∘f∈Domε.又因为

因此ε(C∘f,C∘f)≤ε(f,f),即(ε,Domε)满足压缩性质.由引理4可知,(ε,Domε)是L2(Γ;η)中的Dirichlet形式.

下面讨论(ε,Domε)与加权计数算子的关系.

定理3对∀f∈Domε及∀g∈DomSω,有

ε(f,g)=〈〈f,Sωg〉〉.

(14)

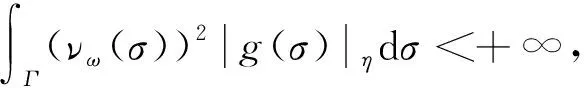
从而g∈Domε,因此DomSω⊂Domε.对∀f∈Domε及∀g∈DomSω,有

即式(14)成立.

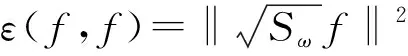
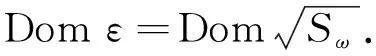
(15)

证明: 由定理3知,对∀f∈Domε,有

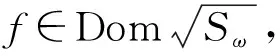
进一步,构造一个C0-半群.对∀t≥0,定义L2(Γ;η)中的强连续算子为

Tt=e-tSω,

其中Sω为二维加权计数算子.易知Tt满足C0-半群的3个条件(定义5),因此算子族(Tt)t≥0=(e-tSω)t≥0是C0-半群.下面给出(ε,Domε)与C0-半群的关系.

定理5若(Tt)t≥0=(e-tSω)t≥0是L2(Γ;η)中的C0-半群,(ε,Domε)是L2(Γ;η)中的Dirichlet形式,则有

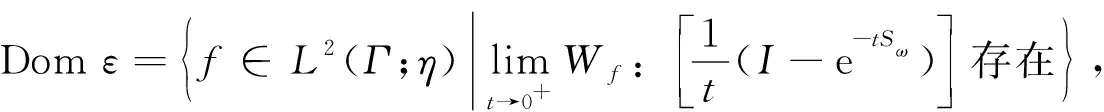
(16)

且

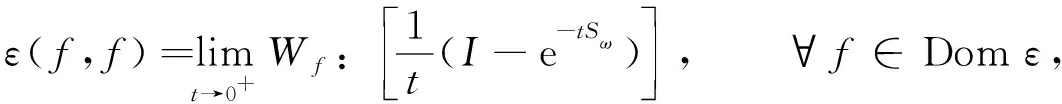
(17)

其中Wf: (x)=〈〈xf,f〉〉,x∈L2(Γ;η),I为L2(Γ;η)中的平凡表示.

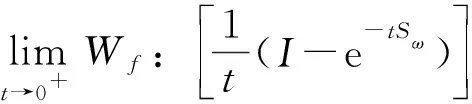
再由定理4可知结论成立.

由注1中二维加权计数算子与一维加权计数算子的关系,可将定理3～定理5的结论推广到一维情形.

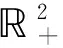
且有如下结论:

(i)ε(f,g)=〈〈f,Nhg〉〉,∀f∈Domε,∀g∈DomNh;

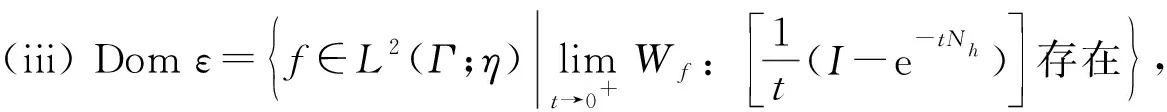
其中Wf: (x)=〈〈xf,f〉〉,x∈L2(Γ;η),I为L2(Γ;η)中的平凡表示.

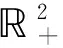
且有如下结论:

(i)ε(f,g)=〈〈f,Ng〉〉,∀f∈Domε,∀g∈DomN;

其中Wf: (x)=〈〈xf,f〉〉,x∈L2(Γ;η),I为L2(Γ;η)中的平凡表示.

证明: 由注1、定理1～定理5可知结论成立.