边替换图的邻和可区别全染色

常景智,杨 超,姚 兵

(1.上海工程技术大学 数理与统计学院,智能计算与应用统计研究中心,上海 201620; 2.西北师范大学 数学与统计学院,兰州 730070)

1 引言与预备知识

图的可区别染色问题是图论中的研究热点[1-2],目前已广泛应用于计算机科学、生命科学以及网络通信等领域.近年来,关于把点和边所染颜色相加的可区别染色问题也得到广泛关注.Karoński等[3]研究了图的邻和可区别边染色,提出了1-2-3猜想.

猜想1(1-2-3猜想)[3]设G为一个阶数至少为3的简单连通图,则gndiΣ(G)≤3.

Kalkowski等[4]证明了阶数至少为3的简单连通图的邻和可区别边色数不超过5.关于邻和可区别边染色的研究目前已有很多结果[5-8].Przybyo等[9]提出了图的邻和可区别全染色的概念,并给出了1-2猜想,证明了该猜想对3-点可染色图、完全图和四正则图均成立,且任意简单连通图的邻和可区别全色数不超过11.Kalkowski[10]得到了任意图的邻和可区别全色数不超过3.程银万等[11]证明了Halin图的邻和可区别全色数不超过2.

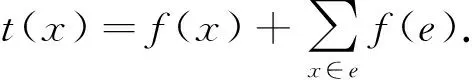
猜想2(1-2猜想)[9]设G为一个简单连通图,则tgndiΣ(G)≤2.

设G和T是两个简单图,i和j为T中的两个固定顶点,满足T-i和T-j同构.用T替换图G的每条边e=(u,v),使得i=u,j=v,所得图称为边替换图[12],记为G[T].由定义可知,当T=P3,即T为3个顶点的路且i和j为P3的两个端点时,G[P3]为图G的剖分图,记为S(G); 当T=C3,即T为3个顶点的圈且i和j为C3的两个端点时,G[C3]为图G的三角扩展图,记为R(G).

设图G=(V(G),E(G))是一个无向简单图,若点集S⊆V(G),且当去掉S后,剩余的子图G-S中不含任何圈,则S称为图G的一个消圈集,同时min{|S||S是图G的消圈集}称为图G的消圈数,记为(G),且此时的消圈集S称为最小消圈集[13].

定义3[14]设点集D为图G的一个消圈集.若点集D为一个独立集,则D称为图G的独立消圈集.

基于上述研究工作,本文首先研究剖分图和三角扩展图的邻和可区别全染色,其次利用独立消圈集法证明当G为任意图,且T为星、圈、路、扇、轮以及部分树时,图G[T]均满足1-2猜想.本文涉及的染色均为非正常的,不失一般性,约定证明过程中凡是未被染色的点和边均染颜色1.

2 剖分图与三角扩展图的邻和可区别全染色

下面介绍独立消圈集法及树的邻和可区别全染色方案.首先,将图的顶点独立划分为森林中的点和独立消圈集A中的点,森林中各树之间无连边,仅森林与独立消圈集A中的点有连边; 其次,根据树的染色算法将森林中的每棵树染色,保证森林中相邻顶点权重差不为2.再将独立消圈集中的点v∈A及其与森林的连边均染为颜色2,使得该点权重为2d(v)+2; 最后,通过讨论森林中点的权重与独立消圈集A中点的权重是否相等,证明图是否满足1-2猜想.

引理1设G是阶数至少为3的简单连通图.若G中相邻点的度均不相同,则tgndiΣ(G)=1.

证明: 将图G中所有边和点均染颜色1,根据定义2易得点v的权重t(v)=d(v)+1.因为G中相邻点的度均不相同,所以G中相邻点权重不同.

引理2设Tn是阶数为n的树,则当n≥3时,

证明: 当Tn中相邻点的度均不同时,由引理1得tgndiΣ(Tn)=1.当树Tn中存在度相同的相邻点时,由于树是二部图,不妨设VT=VA∪VB,其中VA,VB分别为A,B两部的点集合.定义Tn的一个2-全染色如下: 将树中所有边染颜色1,设va∈VA,vb∈VB,对于点的染色: 若d(va)≡0(mod 2),则f(va)=1; 若d(va)≡1(mod 2),则f(va)=2; 若d(vb)≡0(mod 2),则f(vb)=2; 若d(vb)≡1(mod 2),则f(vb)=1.因此可知t(VA)为奇数,t(VB)为偶数,相邻点权重均不相同且权重差不为2,证毕.

定理1设图G为任意简单连通图,则

证明: 当G中无2度点时,S(G)中相邻点的度均不相同.此时由引理1,将S(G)中所有点和边均染颜色1,易得相邻点权重均不相同,即tgndiΣ(S(G))=1.下证当G中存在2度点时,tgndiΣ(S(G))=2.

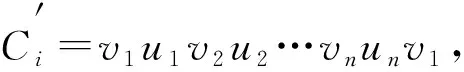
V(S(G))=V(T1)∪V(T2)∪…∪V(Tn)∪A,

其中Ti(i∈[1,n])为树,A为独立消圈集.根据引理2对森林S(G)-A染色,并将独立消圈集A中的点及其与S(G)-A中点的连边均染颜色2,由于上述算法证明了树中每个相邻点的权重差不为2,所以将独立消圈集A中的点与S(G)-A的连边染颜色2后不改变森林中相邻点的权重.又因为森林中与独立消圈集A相邻的点度均为1,故权重不超过5,再由A中点权重最小值为6,易得图S(G)中相邻点权重不同.

定理2设图G为任意简单连通图,则当图G满足1-2猜想时,有tgndiΣ(R(G))=2.

证明: 将图G中的点依次标记为vk(k∈[1,n]).对G中的每条边vivj,通过增加点vij和边vivij,vijvj(i,j∈[1,n],i≠j),可得三角扩展图R(G).要证图R(G)中相邻点权重不同,只需证R(G)中点vi权重可能的取值数目大于其在图G中相邻点vj的个数即可.因为图G满足1-2猜想,因此不失一般性,设v1为图G中的点,d(v1)为点v1的度,根据三角扩展图定义可知,图G中的点经过三角扩展后多了d(v1)条边,把这些边染颜色1或2,则图R(G)中点v1的权重有(d(v1)+1)种不同的取值.易见与点v1相邻点的个数为d(v1)

下证vij与其邻点权重不同.当G不为K2时,点vij可染为颜色1或2,即点vij权重有两种可能,并大于其邻点的个数.由上述证明可知,当G不为K2时,tgndiΣ(R(G))=2; 当G=K2时,R(G)=C3,易得tgndiΣ(C3)=2.

3 几类边替换图的邻和可区别全色数

定理3设图G为任意简单连通图,则当图T为Pn(n>3)时,有tgndiΣ(G[Pn])=2.

证明: 当n>3时,图G[Pn]中必出现相邻点度相同的情形,故tgndiΣ(G[Pn])≥2.下证当图G为任意简单连通图且图T为Pn时,tgndiΣ(G[Pn])=2.首先找出图G[Pn]的一个独立消圈集A1.由定理1可知,设A1为图G的一个消圈集,则A1也为图G[Pn]的一个独立消圈集.此时将图G[Pn]的顶点划分为森林G[Pn]-A1和A1,其中森林内部各树之间无连边,仅独立消圈集A1与森林G[Pn]-A1有连边.根据引理2中树的算法对森林G[Pn]-A1染色,该算法证明了树中每个相邻点的权重差不为2,故将独立消圈集A1中的点及其与G[Pn]-A1中点的连边均染颜色2,从而保证了森林中的各点在加入与A1连边颜色为2后相邻点权重仍不同.因为A1中点度最小为2,所以A1中点权重最小值为6.又因为G[Pn]-A1中与独立消圈集A1相邻点的度均为1,故其权重不超过5,于是易得图G[Pn]中相邻点权重均不相同,即tgndiΣ(G[Pn])=2.

定理4设图G为任意简单连通图,则当图T为Cn(n>3)时,有tgndiΣ(G[Cn])=2.

证明: 用独立消圈集法证明结论成立.首先找出图G[Cn]的一个独立消圈集A2.根据边替换图的定义,i和j为T中的两个固定顶点,满足T-i和T-j同构.通过简单分析可知,当图T为Cn时,图T中任意两点i,j均满足T-i和T-j同构.为保证可找到图G[Cn]的一个独立消圈集A2,不妨取Cn中任意两个不相邻的点为固定点,可得边-圈替换图G[Cn].取A2=V(G),则V(G[Cn])-V(G)为若干个不交路或孤立点,因此A2为图G[Cn]的一个独立消圈集.此时将图G[Cn]的顶点划分为森林G[Cn]-A2和A2,其中森林内部无连边,仅独立消圈集A2与森林G[Cn]-A2存在连边.根据引理2中树的算法对森林G[Cn]-A2染色,该算法证明了树中每个相邻点的权重差不为2,故将独立消圈集A2中的点及其与G[Cn]-A2中点的连边均染颜色2,从而保证了森林中各点在加入与A2连边颜色为2后相邻点权重仍不同.因为A2中点度最小为2,所以A2中点权重最小值为6.又因为G[Cn]-A2中与独立消圈集A2相邻点的度均为1,故其权重不超过5,易得图G[Cn]中相邻点权重均不同,即tgndiΣ(G[Cn])=2.

定理5设图G为任意简单连通图,则当图T为(n+1)阶星Sn时,有

证明: 星Sn的顶点集和边集分别表示为

V(Sn)={v1,v2,…,vn,vn+1},

E(Sn)={vivn+1|i=1,2,…,n}.

当n=2时,有S2=P3,G[S2]=S(G),该情形可见定理1.当n>2时,若dG[Sn](v)≠dG[Sn](vn+1),v∈V(G),则经过边替换后相邻点度均不相同,因此根据引理1可知tgndiΣ(G[Sn])=1; 若存在点vk∈V(G),使得dG[Sn](vk)=dG[Sn](vn+1)成立,则图G[Sn]中存在相邻点度相同的情形,于是可知tgndiΣ(G[Sn])≥2.

下面给出tgndiΣ(G[Sn])=2的染色方案.不妨取星中点v1,vn为固定点,则点vn+1与这两点均相邻.根据边-星替换图G[Sn]的定义可知,图Sn中所取固定点必为图G中的点,不失一般性,记为点v1,将该点本身及关联边均染颜色2,可得权重为t(v1)=2d(v1)+2.易见图G[Sn]-V(G)为森林,根据引理2中树的算法对森林G[Sn]-V(G)染色,对点vn+1染颜色1或2可保证其权重为奇数,同理对点v2,…,vn染颜色1或2可保证其权重为偶数.由t(v1)=2d(v1)+2≡0(mod 2)知,与v1相邻的点vn+1权重为奇数,故此时图G[Sn]中相邻点权重均不同,即tgndiΣ(G[Sn])=2(n>2).

定理6设图G为任意简单连通图,则当图T为(n+1)阶扇Fn时,有tgndiΣ(G[Fn])=2.

证明: 扇Fn的顶点集和边集分别表示为

V(Fn)={v1,v2,…,vn,vn+1},

E(Fn)={vivi+1|i=1,2,…,n-1}∪{vivn+1|i=1,2,…,n}.

当n=2时,图G[F2]=G[C3]=R(G),由定理2可知

tgndiΣ(G[F2])=tgndiΣ(R(G))=2.

下证n>2的情形.根据边替换图的定义可知,当图T为Fn(n>2)时,可取点v1,vn分别为固定点.再由定义知,图G中的任意两个邻点经过边替换后均有如图1所示的结构,其中点v1,vn为图G中的邻点.要证边-扇替换图G[Fn]相邻点权重不同,只需证图1结构中相邻点权重不同,再证两个相邻结构中的邻点权重可区分即可.下面给出全染色方案:

图1 G[Fn]的结构及其染色Fig.1 Structure and coloring of G[Fn]

根据上述全染色方案可得

易知当n>3时,点vn+1的权重均为奇数,且在n=3时取到最小值8.由

t(v1)=2dG[Fn](v1)+2,t(vn)=2dG[Fn](vn)+2

且

dG[Fn](v1)=dG[Fn](vn)≡0(mod 2),

易见仅当dG[Fn](v1)=dG[Fn](vn)=2时才会出现t(v1)=t(v2)=6或t(vn-1)=t(vn)=6的情形,此时只需将点v1或vn重染为颜色1即可.于是有t(v1)=5≠t(v2)=6或t(vn)=5≠t(vn-1)=6.故图G[Fn]中相邻点权重均不同,即tgndiΣ(G[Fn])=2成立.

定理7设图G为任意简单连通图,则当图T为(n+1)阶轮Wn(n>3)时,有tgndiΣ(G[Wn])=2.

证明: 由定理6中扇Fn的定义知,轮Wn的顶点集和边集分别为

V(Wn)=V(Fn),

E(Wn)=E(Fn)∪{v1vn}.

根据边替换图的定义可知,当图T为Wn时,可取点v1,v3分别为固定点.再由定义知,图G中的任意两个邻点经过边替换后均有如Wn的结构,其中点v1,v3为图G中的邻点.要证边-扇替换图G[Wn]相邻点权重不同,只需证如Wn结构中相邻点权重不同,再证两个相邻结构中的邻点权重可区分即可.下面给出全染色方案:

根据上述全染色方案可得对应点权重如下:

易知点vn+1的权重均为奇数,而dG[Wn](v1)=dG[Wn](v3),则有

t(v1)=t(v3)=2dG[Wn](v1)+2,

易见t(v1)=t(v3)≡0(mod 2),此时图G[Wn]中相邻点权重均不同,即tgndiΣ(G[Wn])=2成立.

定理8设图G为任意简单连通图,若树Tn中有两个相邻的叶子点,则tgndiΣ(G[Tn])=2.

证明: 当图T为Tn时,根据图G[Tn]的定义,只需Tn满足i和j为T中的两个固定顶点,且图Tn-i和图Tn-j同构.

当Tn中有两个相邻的叶子点时,不妨设为u1和u2,则Tn-{u1}和Tn-{u2}同构,即图G[Tn]存在.由于树Tn是二部图且不含圈,故易找出图G[Tn]的一个独立消圈集A3.此时,将图G[Tn]的顶点划分为森林点集V(G[Tn])-A3和独立消圈集A3,其中森林内部各树之间无连边,仅独立消圈集A3与森林G[Tn]-A3有连边.利用引理2中的树染色算法对森林G[Tn]-A3进行染色,该算法证明了树中每个相邻点的权重差不为2,故将独立消圈集A3中的点及其与G[Tn]-A3中点的连边均染颜色2,从而保证了森林中的各点在加入与A3连边颜色为2后相邻点权重仍不同.根据染色规则可知,A3中点权重恒为偶数,又因为独立消圈集A3中的点在集合G[Tn]-A3中的邻点权重可利用引理2的证明方法将其调整为奇数,因此图G[Tn]中相邻点权重均不同.