带有Stieltjes积分边界条件和ψ-Caputo导数的分数阶边值问题解的存在性
2023-05-21周宗福
王 宁,周宗福
(安徽大学 数学科学学院,合肥 230601)
0 引 言
分数阶微积分是整数阶微积分的推广,由于分数阶导数具有良好的记忆性质和遗传特性,使得其在物理和工程等领域应用广泛[1-3],关于分数阶微分方程的研究目前已取得了丰富成果[4-9].分数阶导数的定义形式繁多,为克服该问题,Almeida[10]将Caputo分数阶导数与带有核的Riemann-Liouville分数阶导数相结合,并引入ψ-Caputo分数阶导数,研究了它的一些性质,从而将多种形式的Caputo分数阶导数统一起来,促进了具有一般导数形式的分数阶微积分的发展.
文献[11]研究了下列边值问题:

(1)
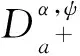

(2)

受上述研究工作的启发,本文考虑如下分数阶微分方程边值问题:

(3)

1 预备知识
定义1[13]令α>0,u为[a,b]上的可积函数,u(t)的α阶ψ-Riemann-Liouville分数阶积分定义为
定义2[13]令α>0,u: [a,b]→为可积函数,u(t)的α阶ψ-Riemann-Liouville分数阶导数定义为

定义3[13]令α>0,若u∈Cn-1[a,b],则u(t)的α阶ψ-Caputo分数阶导数定义为

定义4[10]若u∈Cn[a,b]且α∈,则
若α=n∈,则
引理1[13]令α>0,u: [a,b]→,则下列结论成立:


引理2[10]令α,β>0,u: [a,b]→为可积函数,则:

引理3(Schaefer不动点定理)[14]设X为Banach空间,T:X→X是一个连续的紧映射,{u∈X|u=λT(u),0<λ<1}有界,则T至少存在一个不动点.
引理4令n-1<α (4) 的解为 其中 证明: 由引理1知, (6) 因此, (7) 将式(6)代入式(7)可得 将求出的C0,C1,…,Cn-1代入(6),即知式(5)成立.证毕. 定义算子T:C[a,b]→C[a,b], 由引理4知,T的不动点即为边值问题(3)的解. 为方便,引入以下记号: 假设条件: (H1) 存在常数ξ>0,使得|f(t,x)-f(t,y)|≤ξ|x-y|,t∈[a,b],x,y∈; (H2)ξΛ1(ψ(b)-ψ(a))α<1. 定理1假设条件(H1),(H2)成立,则边值问题(3)在[a,b]上存在唯一解. 先证T:Br0→Br0.∀u∈Br0及∀t∈[a,b],有 因此,‖Tu‖≤ξΛ1(ψ(b)-ψ(a))αr0+Λ2≤r0,即TBr0⊂Br0,从而T:Br0→Br0. 下证边值问题(3)在[a,b]上存在唯一解.令u1,u2∈Br0,t∈[a,b],则 于是 ‖Tu1-Tu2‖≤ξΛ1(ψ(b)-ψ(a))α‖u1-u2‖. 再由假设条件(H2)知,T为压缩映射. 因此,根据Banach压缩映像原理可知,T在Br0中存在唯一的不动点,即边值问题(3)存在唯一解.证毕. 下面给出边值问题(3)至少存在一个解的结果. 引理5T:C[a,b]→C[a,b]为全连续算子. 证明: 首先证明T连续.任取{un}⊂C[a,b]且un→u∈C[a,b](n→+∞),则∀t∈[a,b],有 从而 ‖Tun-Tu‖≤Λ1(ψ(b)-ψ(a))α‖f(·,un(·))-f(·,u(·))‖. 由f的连续性可知‖Tun(t)-Tu(t)‖→0(n→+∞),进而T连续. 从而T(Br)有界,即T(Br)中的函数一致有界. 下证T(Br)中的函数等度连续.定义 ∀t1,t2∈[a,b],不妨设t1 当t2→t1时,|(Tu)(t2)-(Tu)(t1)|→0,因此T(Br)等度连续. 由Arzela-Ascoli定理可知T(Br)列紧,故T为紧算子,所以T:C[a,b]→C[a,b]为全连续算子.证毕. 假设条件: (H3) 存在常数r1>0及连续单调递增函数φ: [0,+∞)→[0,+∞),使得 |f(t,v)|≤φ(|v|)+r1, ∀t∈[a,b], ∀v∈; (H4) 存在常数r2>0,使得当r>r2时,r>Ω1+Ω2(φ(r)+r1),其中 定理2假设条件(H3),(H4)成立,则边值问题(3)在[a,b]上至少有一个解. 证明: 由引理5知,T:C[a,b]→C[a,b]为全连续算子.令Δ={u∈C[a,b]:u=λTu,λ∈(0,1)},下证Δ有界. 由Δ的定义知,∀u∈Δ,∃λ∈(0,1),使得u=λTu,故∀t∈[a,b],u(t)=λTu(t),有‖u‖≤‖Tu‖.由引理5的证明知,‖Tu‖≤Ω1+Ω2‖f(·,u(·))‖.利用假设条件(H3)可得,‖u‖≤Ω1+Ω2(φ(‖u‖)+r1),由假设条件(H4)知,‖u‖≤r2.所以Δ有界. 由Schaefer不动点定理可知T在C[a,b]中至少存在一个不动点,即边值问题(3)在[a,b]上至少有一个解.证毕. 考虑下列边值问题: (8) ∀u,v∈,t∈[0,1],有 由定理1可知边值问题(8)在[0,1]上存在唯一解.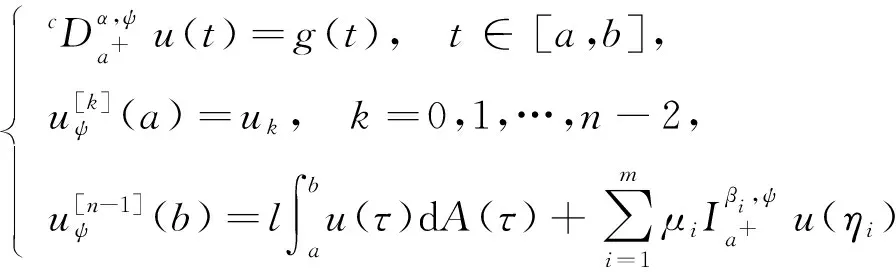




2 主要结果

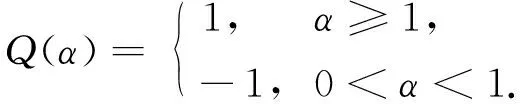
3 应用实例

