课程质量在材料对幼儿数学发展影响中的中介效应分析
2023-05-21陈德枝王欣怡向婉怡
陈德枝 王欣怡 向婉怡
[摘 要] 课程质量是重要的幼儿园教育过程质量要素,对幼儿发展有重要影响。为验证班级课程质量和数学领域课程质量在材料与幼儿数学发展之间的中介效应,本研究采用分层抽样方法,从我国5个省(市、自治区)抽取302个班级和1 776名幼儿,运用相关评价标准和量表对班级课程质量、数学领域课程质量、材料、幼儿数学发展水平进行测评。对所得数据的多水平线性模型分析结果发现,数学领域课程质量在材料与幼儿数学发展之间具有完全中介效应,班级课程质量没有中介效应;材料虽然对班级课程质量和数学领域课程质量都有显著的正向影响,但是对幼儿数学发展没有直接作用,它需要通过数学领域课程质量才能对幼儿数学发展起作用。在幼儿园数学教育实践中,教师在设计和实施数学领域课程时不仅要考虑材料的丰富多样性,更应为幼儿提供多种形式的具有发展适宜性的课程活动,并学会开展科学有效的课程评价,以让幼儿获得更好的发展。
[关键词] 课程质量;班级课程质量;数学领域课程质量;幼儿数学发展
一、问题提出
幼儿园教育质量指幼儿园教育活动是否满足幼儿身心健康发展和学习需求及其满足程度,通常包含结构质量和过程质量。[1][2]幼儿园教育质量对儿童早期发展具有重要意义。已有研究表明,过程质量如师幼互动、课程、学习环境、健康与安全、家长参与等对儿童的学习发展具有更为直接、重要的影响。[3][4]班级课程质量作为过程质量的重要组成部分,是提高幼儿园教育质量、促进幼儿全面和谐发展的关键。[5]班级课程质量既指整个班级的课程质量,也包括在班级开展的各学习领域的课程质量,如数学领域课程质量。幼儿数学发展指幼儿对数的知识、概念和技能的理解与运用能力,[6]一般包括数、数量关系、排序、分类、形状、时间、空间等方面。数学发展是幼儿全面发展的重要组成部分,不仅影响着幼儿未来的数学学习,而且能预测其以后的学业和生活水平。[7][8]已有研究发现,班级课程质量与幼儿语言、识字、数学技能的发展相关,[9]对幼儿前阅读、早期数学概念、非言语推理、读写技能等均有显著的正向预测作用。[10][11]接受良好的数学教育能促进儿童数学认知的发展,[12]高质量的教学与互动对儿童早期数学发展具有积极的预测效应。[13][14]
班级课程质量影响因素包括环境创设、材料资源等。[15]环境和材料可以为儿童创造不同的学习机会,让儿童以各种方式学习。[16]首先,环境是教育中的隐形课程,儿童发展正是儿童与周围环境相互作用的过程。[17]幼儿园班级物质环境创设的好坏可以体现出幼儿园教育质量的高低,优质的物质环境可以促进幼儿发展。[18]其次,材料是幼儿发现和了解世界的媒介,材料的投放方式会影响幼儿园过程性教育质量。[19]与此同时,区域活动是幼儿园实施数学教育的途径之一。[20]材料作为幼儿园数学区域活动开展的关键因素和物质基础,影响着幼儿园数学教育质量。[21]此外,幼儿园和班级层面的其他因素也会对班级课程质量造成影响。如已有研究发现,幼儿园的地理位置、办园性质会造成班级课程质量的差异,[22]并且不同学习领域的教育质量会因办园性质的不同而有所不同。[23]从班级层面来说,师幼比会影响教师对幼儿的关注以及评价的准确性,从而影响到教师组织的集体教学活动的质量。[24]教师作为班级中的重要人物,其学历能正向影响班级课程质量,[25]学历越高的教师往往能提供更高质量的教学。[26]
教育机构、家庭和幼儿自身对其数学发展均具有重要影响。[27]在教育机构方面,已有研究表明园所等级与质量、教师及师幼互动等因素在一定程度上会影响幼儿数学发展。[28][29][30]在家庭教育环境中,已有研究表明家庭社会经济地位、父母受教育水平、教育(教养)观念和亲子互动等直接或间接影响幼儿数学发展水平。[31]其中,大多数研究结果显示父母的受教育水平会影响孩子的数学发展水平。[32]相比较而言,母亲的学历被认为具有更直接的影响。[33]此外,幼儿的个体特征也会影响其数学发展。已有研究发现幼儿的数学能力会随年龄的增长而提高。[34][35]大多数研究没有发现幼儿数学发展水平存在性别差异,[36]不过也有相反的观点。[37][38]
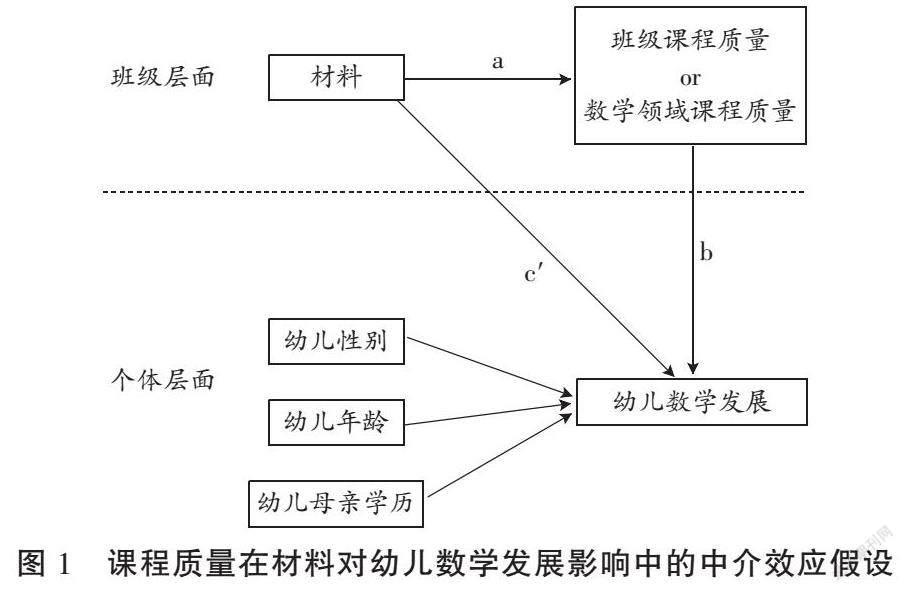
综上所述,班级课程质量对幼儿数学发展具有积极的促进作用,而学习材料的丰富多样性又将影响班级课程质量。那么,材料和班级课程质量究竟是如何影响或促进幼儿数学发展的呢?班级课程质量对幼儿数学发展的作用路径或机制如何?目前相关研究很少。由于班级课程质量和材料是班级层面变量,而性别、年龄、幼儿家庭背景如母亲学历等属于幼儿个体层面变量,考虑变量和测量数据的嵌套性,本研究拟构建如图1所示的多水平中介效应模型,提出研究假设1:班级课程质量在材料和幼儿数学发展之间起中介作用。由于班级课程质量包含幼儿各学习领域的教育质量,所以本研究还会在假设1的基础上用班级层面的数学领域课程质量代替班级课程质量作为中介变量,进一步考察数学领域课程质量在材料和幼儿数学发展之间的中介作用,由此提出研究假设2:数学领域课程质量的中介效应比班级课程质量更显著。本研究不仅能为幼儿园课程质量促进幼儿数学发展提供理论支持,而且能为相关教育实践提供具体可行的建议。
二、研究方法
(一)研究对象
本研究采用分层抽样的方法,在我国不同地域的5个省(市、自治区)及其城乡共抽取了102所幼儿园,其中公办园59所,民办园43所。随后,在每所幼儿园随机抽取大、中、小班各1个。每个班级随机抽取男、女童各3名。剔除无效数据后,最终男童897名,女童879名,共计1 776名。研究对象的平均月龄为60.23,标准差为17.11。
(二)研究工具
1. 班级和数学领域课程质量评价工具。
班级课程质量评价工具由中国学前教育研究会研制的《走向优质——中国幼儿园教育质量评价标准》(以下简称《优质标准》)中的“课程促进”质量领域的部分项目构成。这些项目从课程领导、课程设计、课程实施、课程评价、健康、语言、社会、科学、艺术9个方面对班级课程质量进行评价。数学领域课程质量测评采用该“课程促进”质量领域的科学項目的“形状和空间”“分类、排序和模式”两个子项目。这两个子项目从数学活动、数学语言、数学教育途径、数学材料以及幼儿操作数学材料的时长等方面对班级数学领域课程质量进行评价。材料变量的测量工具由《优质标准》的“环境支持”质量领域的“材料投放”项目构成。该项目主要从材料的数量、种类、适宜性、个性化、收纳摆放以及安全维护和更新等方面对材料质量进行测评。在本研究中,“课程促进”质量领域的α系数为0.934,“环境支持”质量领域的α系数为0.770。[39]
2. 幼儿数学发展测评工具。
本研究采用《基于研究的早期数学测验-简洁版》(Researchbased Early Math AssessmentShort Form)对幼儿数学发展水平进行测量。[40]该量表被认为是当前应用较为广泛的学前儿童数学发展测评工具。[41][42]该量表从排序、口头计数、计数策略、算术及数字认知和敏感等方面进行评估,其计分方式为幼儿正确作答计1分,幼儿回答错误或没有作答计0分。在本研究中,该量表的内部一致性α系数为0.96,KMO值为0.97,探索性因素分析共提取5个因子,总方差解释率为62.52%。
3. 《幼儿家长问卷》。
本研究自编《幼儿家长问卷》,主要用于收集研究对象的家庭基本信息。该问卷的填写与班级课程质量测评、幼儿数学发展测评在同一天内完成。
(三)研究过程
1. 班级课程质量测评过程。
正式测评开始前,课题组对参与测评的评估员进行了统一、严格的测评培训,涉及测评方法、测评指标解读、现场试测培训等。已有研究结果表明,两人一组进行测评是经济有效的。[43]本研究中,班级课程质量测评采用两人一组的方式,先由两人各自独立评分,然后两人再讨论确定最终的测评结果。测评是在不干扰班级正常活动的情况下进行的,时间一般从早上8:00至下午4:00。本轮测评中,评估员之间的评分一致性为0.819~0.986,达到了可接受水平。[44]
2. 幼儿数学发展水平测评过程。
在班级课程质量测评的当日,由幼儿发展测评人员严格按照测评指导语和流程对每位抽样幼儿进行数学发展水平测评。为减少干扰,测试在环境安静且幼儿熟悉的活动室中进行。测试开始前,测评人员通过询问幼儿姓名等活动熟悉被试,以缓解其紧张感,并填写被试的基本信息。测评时间一般为10~20分鐘。若测评过程中幼儿出现疲劳、注意力下降等问题,测评人员会让幼儿适当休息后再继续。对于本次参与测评的所有幼儿,本研究均已取得其父母的书面同意。
(四)数据处理
本研究主要运用SPSS 26.0和Mplus 8.0等软件进行数据分析。
三、研究结果与分析
(一)各变量的描述性统计分析
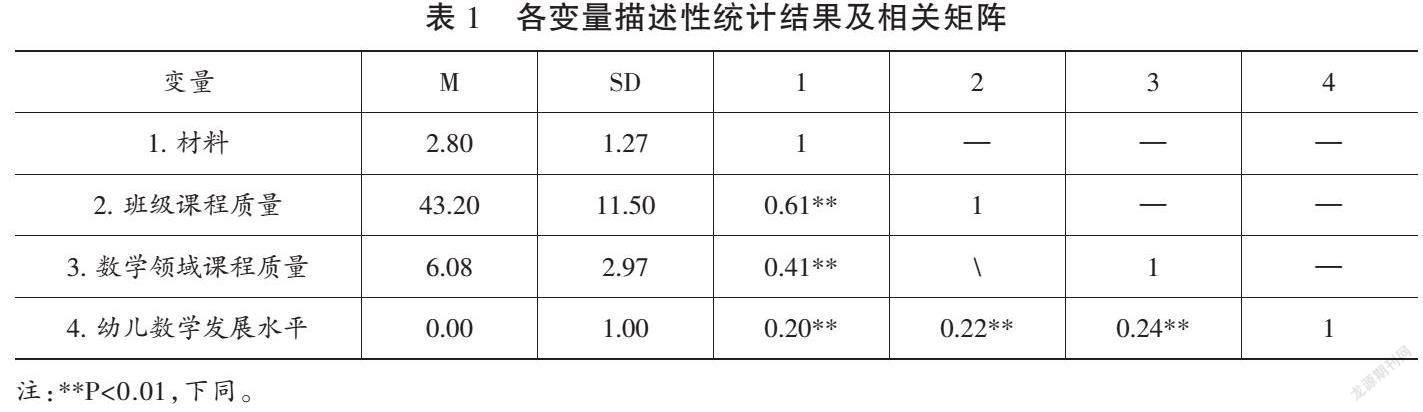
从表1可知,班级课程质量、材料与幼儿数学发展水平之间均存在两两显著正相关(P<0.01)。同时,数学领域课程质量、材料与幼儿数学发展水平之间也均存在两两显著正相关(P<0.01)。
(二)多水平线性模型分析结果
1. 零模型。
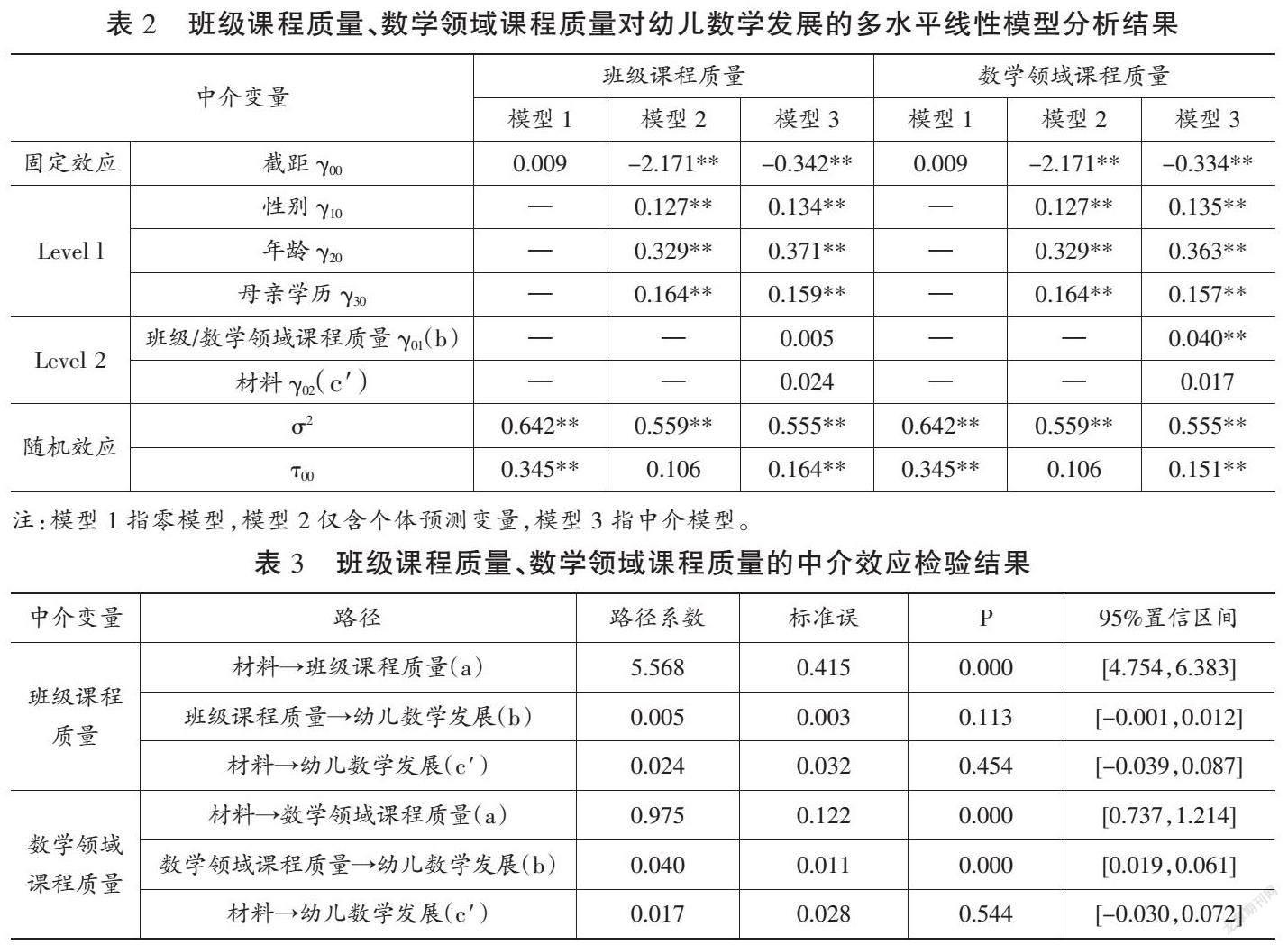
零模型通常用于确定使用多水平线性模型(Multilevel Linear Model,MLM)分析数据是否可行,一般会采用ICC(■)指标估计值进行衡量。如表2所示,本研究的零模型(即模型1)的ICC值为0.35。依据Cohen(1988)的标准,当ICC>0.138时,表示高度关联强度。[45]这说明本研究的组间差异(即班级水平之间的差异)显著,需要采用MLM进行分析。
2. 纳入个体预测变量的分析结果。
在零模型的第一层方程中纳入幼儿个体预测变量(性别、年龄、母亲学历),以考察幼儿个体特征对其数学发展的影响。结果如表2中的模型2所示,幼儿性别与年龄、母亲学历对其数学发展均有显著的正向影响作用,这与已有结论相一致。[46][47]另外,在这3个预测变量中,路径系数最大的是年龄(0.329,P<0.01),这一结果也得到了已有研究的广泛支持。[48][49][50]
3. 班级课程质量和数学领域课程质量的中介效应。
依据方杰等人提出的多水平中介效应模型检验方法,[51]本研究分别对班级课程质量和数学领域课程质量进行中介效应分析和检验。从表2中以班级课程质量为中介变量的模型3可知,材料对幼儿数学发展的路径系数为0.024(P>0.05),这说明材料对幼儿数学发展没有显著的直接作用;班级课程质量对幼儿数学发展的路径系数为0.005(P>0.05),这说明班级课程质量对幼儿数学发展也没有显著的预测作用。从表3可知,材料对班级课程质量的路径系数为5.568(P<0.01),这说明材料对班级课程质量具有显著的正向预测作用。总体来看,班级课程质量在材料和幼儿数学发展之间不存在中介效应。
从表2中以数学领域课程质量为中介变量的模型3可知,材料对幼儿数学发展的路径系数为0.017(P>0.05),这说明材料对幼儿数学发展没有显著的直接作用;数学领域课程质量与幼儿数学发展的路径系数为0.040(P<0.01),这说明数学领域课程质量对幼儿数学发展具有显著的正向预测作用。从表3可知,材料对数学领域课程质量的路径系数为0.975(P<0.01),这说明材料对数学领域课程质量也具有显著的正向预测作用。对该结果的进一步分析显示,数学领域课程质量在材料和幼儿数学发展之间起完全中介作用,中介效应值为0.69,占总效应的ab/(ab+c′)=69.6%。
比较班级课程质量和数学领域课程质量的中介检验结果,可以发现,班级课程质量没有发挥任何中介作用,这说明研究假设1不成立;数学领域课程质量具有完全的中介效应,能够解释将近70%的变异,这说明相比于班级课程质量,数学领域课程质量对幼儿数学发展具有更加重要的作用,证明研究假设2成立。此外,上述研究结果还显示,材料虽然对班级课程质量和数学领域课程质量都有显著的正向影响,但是对幼儿数学发展并无任何直接作用,它需要通过数学领域课程质量促进幼儿数学发展。
四、讨论
(一)班级课程质量对幼儿数学发展的作用机制
本研究与已有研究结果一致的是,材料变量对班级课程质量和领域课程质量均有正向预测作用。[52][53]这意味着材料仅是影响课程质量的因素之一。另外,无论以班级课程质量还是数学领域课程质量为中介变量,材料变量对幼儿数学发展均没有直接作用。这表明当班级投放的材料种类、数量以及层次越丰富时,虽然班级课程质量和领域课程质量都会随之有所提高,但是并不能直接提高幼儿的数学发展水平。另外,本研究还检验了幼儿个体特征变量与其数学发展的关系,结果表明幼儿的性别、年龄及母亲学历对其数学发展具有正向影响。其中,男童比女童表现出更高的数学发展水平,这一结论和周晶等人的研究结果一致,[54][55]但是也有研究持相反意见。[56][57][58]除此之外,本研究验证了母亲学历对幼儿数学发展具有积极影响,[59]这可能是因为社会角色分工导致母亲有更多的机会与时间陪伴和教育儿童,而母亲的学历会影响其教养观念与方式及亲子互动质量,从而影响幼儿的数学认知发展。不过,也有少量研究认为父亲学历的影响更显著。[60]
(二)班级课程质量与领域课程质量的不同中介作用
本研究发现,班级课程质量在材料变量和幼儿数学发展之间没有中介效应,数学领域课程质量则具有完全的中介效应。班级课程质量之所以没有中介效应,可能与班级课程质量的构成有关。在本研究中,班级课程质量不仅包含数学领域课程质量,还包含了健康、语言、艺术、科学、社会等领域的课程质量,这或许是造成班级课程质量影响不显著的主要原因。这也意味着,丰富材料类型、结构和投放方式等可以提高班级课程质量,但是仍然只有通过适宜的数学领域课程设计和实施,才能真正地支持和促进幼儿数学发展。同时,这一研究结果也表明,相较于语言、社会等领域的学习,幼儿的數学学习更加依赖其对数学材料的操作。[61][62]总之,要提高幼儿数学发展水平,教师不能仅仅丰富材料,还应设计和实施具有发展适宜性的数学领域课程。这与当前教育部颁布的《幼儿园保育教育质量评估指南》强调过程性质量不谋而合,[63]也进一步验证了该观点的科学性。
从布朗芬布伦纳的生态学视角来看,儿童的发展是嵌套在一个个相互影响的环境系统中,并持续不断地与周围环境和系统发生相互作用的过程。[64]如前所述,班级课程质量与幼儿发展关系的探索是一项涉及若干变量的研究。家庭因素不仅包括母亲学历,还包括家庭经济收入、文化价值观和习俗等;教育环境还包括教师学历、班级师幼比等,这些因素也会对幼儿发展产生重要影响。限于篇幅,本研究未有涉及,有待未来做进一步的探索。
五、实践启示
(一)对数学领域课程设计的实践启示
本研究结果显示,数学领域课程质量在材料对幼儿数学发展的影响中起完全中介作用。这意味着在幼儿园教育实践中,教师在设计课程时不仅要为幼儿提供丰富多样、层次分明的材料,而且要重点考虑能引发幼儿多样化、创造性探究的课程活动,以为幼儿的数学学习和发展创造更多的机会和可能。除此之外,进行课程设计时,教师还要深度挖掘材料对幼儿发展所具有的潜在价值,多关注材料中可能蕴含的师幼互动、同伴交流的机会。当然,课程设计除了安排专门的数学领域活动外,还需在其他领域中渗透这些数学内容,培养幼儿的知识联系与迁移的能力。如幼儿学习数、量及数量关系时,教师可以在语言领域活动中结合绘本故事中事物的特点(如小动物有几个?大树有几棵?),让幼儿通过唱数的方式将其特征描述出来,在渗入相关知识的同时,教师通过数学语言的使用支持幼儿的数学学习和发展。
(二)对数学领域课程实施的实践启示
课程实施是实现预期课程目标的基本途径,也是课程“再设计”的过程。[65][66]操作实践是学前儿童的主要学习方式。数学相较于其他学习和发展领域,需要儿童更多地从操作中获得相应经验。[67]在数学领域课程实施中,教师应尽可能地组织和实施探究性的数学学习活动,给予幼儿操作的机会。为此,教师不仅要根据年龄、兴趣、经验为幼儿选择操作性较强的材料,更要促进幼儿亲自动手操作,并提供相应的支持,以激发幼儿不断探索新事物的意识,启发幼儿思维,促使其主动构建数学认知。
已有研究发现目前幼儿园数学领域课程大多是通过集体教学活动实施的,常常忽视了生活活动、区域活动、游戏活动也是幼儿数学教育的主要途径。[68]数学知识存在于生活的各个角落之中,幼儿的数学认知与其生活的环境密切相关。教师应注意将幼儿的数学学习与现实生活联系起来,在日常交流中运用数学语言,帮助幼儿积累相关的数学经验。例如,在学习形状和空间时,教师就可以借助幼儿生活中的具体事物,促进幼儿对形状和空间特征的感知(如黑板是正方形的还是长方形的?)。把幼儿的数学学习融入游戏之中也是一种有效的数学教育方法。如通过开烧烤店进行商品与钱币交换的角色游戏,幼儿就可以学会简单的计算,并巩固其关于数与量的知识。让幼儿以游戏的方式进行学习,既增加了数学学习的趣味性,也能让幼儿运用数学知识解决游戏中遇到的简单问题,体验成功,从而激发幼儿数学学习的兴趣。
(三)对数学领域课程评价的实践启示
本研究结果在一定程度上说明了《优质标准》数学领域课程质量评价的有效性,这为实践者进行课程自我评价或内部评价提供了重要参考和启示。首先,就数学领域课程质量评价内容来说,《3~6岁儿童学习与发展指南》是《优质标准》数学领域课程质量评价的主要依据,教师应结合幼儿数学学习和发展特点,并基于幼儿园数学教育活动的实际情况,制定相应的评价内容,这是保证评价有效性和科学性的前提。《优质标准》数学领域课程质量评价的内容十分具体,同时又不脱离国内幼儿园的教育实践,因此这些评价项目和指标十分值得幼儿园在实践中广泛采纳与应用。其次,就评价方式和方法来说,《优质标准》数学领域课程质量评价不仅综合运用了多种方式方法,如观察法、访谈法和文本分析法等,而且其对一个指标的评价往往是多种方法的相互取证,以获得更准确、有效的评价结果。这为幼儿园课程自我评价或内部评价提供了评价方式方法的良好示范,也值得幼儿园在教育实践中学习、借鉴和运用。
参考文献:
[1]刘霞.托幼机构教育质量评价概念辨析[J].学前教育研究,2004(05):5-7.
[2]李克建.中国托幼机构教育质量评价研究[M].北京:北京师范大学出版社,2017:2-4.
[3][5]周欣.托幼机构教育质量的内涵及其对儿童发展的影响[J].学前教育研究,2003(01):34-38.
[4]项宗萍.从“六省市幼教机构教育评价研究”看我国幼教机构教育过程的问题与教育过程的评价取向[J].学前教育研究,1995(02):31-35.
[6][27]周欣.儿童数概念的早期发展[M].上海:华东师范大学出版社,2004:1-2,252-274.
[7]BOOTH J L, SIEGLER R S. Developmental and individual differences in pure numerical estimation[J]. Developmental Psychology,2006,42(1):189-201.
[8]RITCHIE S J, BATES T C. Enduring links from childhood mathematics and reading achievement to adult socioeconomic status[J]. Psychological Science,2013,24(7):1301-1308.
[9][26]ROBERT C, CARR, et al. Cumulative classroom quality during prekindergarten and kindergarten and childrens language, literacy and mathematics skills[J]. Early Childhood Research Quarterly,2019,47(2):218-228.
[10]SYLVA K, SIRAJBLATCHFORD I, TAGGART B, et al. Capturing quality in early childhood through environmental rating scales[J]. Early Childhood Research Quarterly,2006,21(1):76-92.
[11]MELHUISH E C, SYLVA K, SAMMONS P, et al. Preschool influences on mathematics achievement[J]. Science,2008,321(5893):1161-1162.
[12][28][48]周欣,黃瑾,赵振国,等.大班儿童数学认知的发展[J].幼儿教育(教育科学),2009(33):35-39.
[13][29]BURCHINAL M R, MAGNUSON K A, POWELL D, et al. Early childcare and education[M]. New Jersey: Wiley,2015:223-267.
[14][30]K LI, Y PAN, B HU, et al. Early childhood education quality and child outcomes in China: evidence from Zhejiang province[J]. Early Childhood Research Quarterly,2016,36(3):427-438.
[15]王雨.幼儿园课程质量保障体系的个案研究[D].南京:南京师范大学,2016:42-43.
[16]ANDERSSON M. The Early Childhood Environment Rating Scale (ECERS) as a tool in evaluating and improving quality in preschools[D]. The Swedish: Stockholm Institute of Education,1999:1-30.
[17]胡娟.论环境及其创设对儿童发展和教育的价值[J].教育科学,2002(02):61-64.
[18]王文娟.幼儿园班级环境创设的作用探究[J].文化创新比较研究,2019(22):131-132.
[19]韩茜.运用游戏材料的投放提高幼儿园过程性教育质量[J].开封教育学院学报,2015(12):213-214.
[20]张慧和,陈国强,朱琍瑶.幼儿园数学教育资源[M].北京:人民教育出版社,2016:1-2.
[21]肖韵诗.幼儿园大班数学区域活动材料投放的行动研究[D].重庆:西南大学,2021:3-4.
[22]原晋霞.我国幼儿园课程质量现状探索与提升建议[J].学前教育研究,2021(01):43-56.
[23]刘焱,李志宇,潘月娟,等.不同办园体制幼儿园班级教育环境质量比较[J].学前教育研究,2008(08):8-11.
[24]李相禹,刘焱.师幼比对幼儿园集体教学质量影响的实证分析[J].学前教育研究,2016(05):3-14.
[25]潘月娟,刘焱,胡彩云.幼儿园结构变量与教育环境质量之间的关系研究——以山西省幼儿园为例[J].学前教育研究,2008(04):3-10.
[31]黄瑾.家庭与儿童早期数学认知能力发展[J].幼儿教育(教育科学),2006(11):45-48.
[32]刘文,秦梦嫄,陈楠,等.幼儿数认知发展特点及其促进:平板电脑与面对面教学的比较[J].学前教育研究,2018(11):3-14.
[33][36][59]张华,庞丽娟,许晓晖,等.家庭生态环境与儿童早期数学认知能力[J].北京师范大学学报(社会科学版),2005(03):55-61.
[34][37][49][54]周晶,赵振国,郭力平.5~7岁儿童数学过程性能力的发展水平与年龄特点[J].学前教育研究,2020(12):72-81.
[35]黄瑾.学前儿童数学教育[M].上海:华东师范大学出版社,2007:1-3.
[38]周欣,康丹.儿童早期数学学习困难成因与干预[M].上海:华东师范大学出版社,2015:72-78.
[39][44]陈德枝,李克建,周兢.《走向优质——中国幼儿园教育质量评价标准》的测量学属性分析——基于我国100所幼儿园与1670名儿童的测评数据[J].学前教育研究,2021(01):3-16.
[40]SARAMA J, CLEMENTS D H. Interventions in early mathematics: avoiding pollution and dilution[M]. Amsterdam: Elsevier,2017:95-126.
[41]CLEMENTS D H, SARAMA J H, LIU X H. Development of a measure of early mathematics achievement using the Rasch model: the ResearchBased Early Maths Assessment[J]. Educational Psychology,2008,28(4):457-482.
[42]WEILAND C, WOLFE C B, HURWITZ M D, et al. Early mathematics assessment: validation of the short form of a prekindergarten and kindergarten mathematics measure[J]. Educational Psychology,2012,32(3):311-333.
[43]CHEN D, HU B Y, FAN X, et al. Measurement quality of the Chinese Early Childhood Program Rating Scale: an investigation using multivariate generalizability theory[J]. Journal of Psychoeducational Assessment,2014,32(3):236-248.
[45]LEBRETON J M, SENTER J L. Answers to 20 questions about interrater reliability and interrater agreement[J]. Organizational Research Methods,2008,11(4):815-852.
[46]CROOK C J. The role of mothers in the educational and status attainment of Australian men and women[J]. The Australian and New Zealand Journal of Sociology,1995,31(2):45-73.
[47][55]康丹,周欣,田丽丽,等.《早期儿童数学能力测试(中文版)》对上海市5~6岁儿童的适用性研究[J].幼儿教育(教育科学),2014(06):39-45.
[50][56]张亚杰.5~6岁儿童数学元认知知识的发展研究[J].早期教育(教科研版),2017(10):11-15.
[51]方杰,张敏强,邱皓政.基于阶层线性理论的多层级中介效应[J].心理科学进展,2010(08):1-10.
[52][61]吴慧鸣.操作法的原理及其在幼儿数学教育中的应用[J].学前教育研究,1995(06):2-3.
[53][62][67]黄瑾.关注核心经验,促进儿童的数学学习[J].幼儿教育(教育科学),2016(01):18-20.
[57]张华,庞丽娟,陶沙,等.儿童早期数学认知能力的结构及其特点[J].心理学报,2003(06):810-817.
[58]张馨尹.农村5~6岁幼儿数概念发展研究[D].武汉:华中师范大学,2013:30-31.
[60]HU Y, BEHRMAN J R, ZHANG J. The causal effects of parents schooling on childrens schooling in urban China[J]. Journal of Comparative Economics,2021,49(1):258-276.
[63]中華人民共和国教育部.关于印发《幼儿园保育教育质量评估指南》的通知[EB/OL].(2022-02-15)[2022-08-30].http://www.moe.gov.cn/srcsite/A06/s3327/202202/t20220214_599198.html.
[64]BRONFENBENNER U. The ecology of human development experiments by nature and design[J].Children & Youth Services Review,1979,2(4):433-438.
[65]施方良.课程理论——课程的基础、原理与问题[M].北京:教育科学出版社,1996:130-131.
[66]李臣之.课程实施:意义与本质[J].课程·教材·教法,2001(09):13-17.
[68]牟晓峰.幼儿园数学教育课程实施的现状研究[D].烟台:鲁东大学,2012:9-12.
Abstract: Curriculum qualities are recognized as a kind of important process quality factor that can influence preschool education and childrens development. To explore the mediation effects of class curriculum quality and mathematics curriculum quality in the influence of materials on childrens mathematical development, a total of 302 classes and 1,776 children were selected from five provinces in China. The multilevel mediating effect model was used to analyze the evaluation results. Its found that the quality of mathematics curriculum has a complete mediating effect in the mechanism of materials on childrens mathematical development, while the quality of class curriculum has no mediating effect. Based on the research results, suggestions are finally put forward for curriculum practice and evaluation in kindergarten.
Key words: curriculum quality, class curriculum quality, the quality of mathematics curriculum, childrens development on mathematics
(责任编辑:赵南)
