基于LRTC-TNN的瞬时水流量数据连续插值方法

赵金伟,刘杰东,邱万力,黑新宏*

(1.西安理工大学 计算机科学与工程学院,陕西 西安 710048;2.网络计算与安全技术陕西省重点实验室,陕西 西安 710048)

0 引 言

对水厂管道瞬时水流量数据的合理利用和分析是构建城市科学供水系统的基础,是城市用水生产调度的科学依据,是解决城市用水供求关系的关键。然而,在瞬时水流量数据的采集、存储、整理等阶段容易引入缺失值。这将直接影响到水流量分析和预测等下游任务的准确性、有效性、科学性。城市供水系统、水网系统的搭建也会失去来自于数据的有效参考。国内外在时间序列数据缺失值插补问题的研究非常多,但专门针对上游任务中水流量数据连续缺失值的插补问题的研究工作相对较少。因此,急需更为有效的水流量连续缺失值的解决方案,为水流量分析与挖掘等下游任务和工业应用提供准确、完整的数据。

从数据采集的过程可知,瞬时水流量数据具有较强的时间序列特性,但同时它也与地域、人口密度、风土人情、气候特点有很大关系。如果只考虑时间特征,会发现它具有非线性和随机波动的特点,这就为瞬时水流量缺失值的插补带来了困难[1]。近年来,Kabir等人[2]提出用单一均值插补、多重插补等方法插补水流量数据中的缺失值。王志良等人[3]提出采用各种时间序列插补方法对水文站流量缺失数据进行补全。吴若景等人[4]从时空分布的角度构建网络模型插补水文监测站径流量数据的缺失值。对瞬时水流量数据缺失值处理方法的研究,大致可分为三类。第一类,直接采用零值、均值或中位数代替瞬时水流量数据中的缺失值。第二类,采用经典的机器学习或深度学习方法插补缺失值。第三类,利用基于时间序列的经典算法、机器学习和深度学习方法对瞬时水流量数据中的缺失值进行插补。然而,第一类方法相对其它两类简单粗糙,容易造成统计特征和分布特征的偏差,其结果往往易于陷入局部最优[5-6]。第二类方法未考虑瞬时水流量数据时间序列特性,将其看作常规缺失值进行处理,无法有效利用数据本身的特点,导致插补结果不准,甚至欠拟合或过拟合。第三类方法虽然充分考虑到了瞬时水流量数据的时间序列特性,强化了数据之间的时间依赖性,但弱化了特征之间的其它相关性。

基于瞬时水流量数据集的低秩假设,该文提出一种基于非凸低秩张量补全模型(Nonconvex Low-Rank Tensor Completion Model-Truncated Nuclear Norm,LRTC-TNN)的瞬时水流量连续缺失值插补方法。创新如下:第一,在低秩张量补全模型(Low-Rank Tensor Completion Model,LRTC)的基础上引入了适用于瞬时水流量数据集的截断核范数(Truncated Nuclear Norm,TNN),该引入不仅能使LRTC很好地保留重要信息,也不会导致次要信息的丢失,这样LRTC便能更有效地提取到空间信息,掌握数据的特征相关性。第二,重新定义了瞬时水流量数据的时空关系,并利用提出的LRTC-TNN模型对含有连续缺失值的瞬时水流量数据进行处理。这些改进不仅能使LRTC-TNN完美地兼容瞬时水流量数据集,而且能充分发挥LRTC-TNN方法高维特性的优势,很好地利用时间序列特性把握数据的时间依赖性,同时可以有效地提取数据的特征相关性,一定程度上解决了第三类方法中存在的问题,为处理含有连续缺失值的瞬时水流量数据提供了有效方案。

1 基本原理

1.1 符号定义与标注

1.2 非凸低秩张量补全模型

非凸低秩张量补全模型(Nonconvex Low-Rank Tensor Completion Model,LRTC)与低秩矩阵补全的原理类似,LRTC本质上是建立在输入张量的低秩假设上,是一种张量处理模型。对于有部分观测值的三阶张量Y∈RM×N×T,LRTC模型表示为:

(1)

(2)

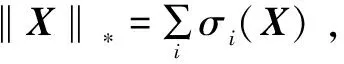
1.3 LRTC-TNN

虽然核范数最小化在矩阵和张量数据的插补任务中很有效,但研究发现,通过基于奇异值的某些非凸函数有更好的效果[9-11]。由于截断核范数(Truncated Nuclear Norm,TNN)[10,12]具有更高的灵活性,不但能保留大的奇异值还会引入较小的奇异值,避免信息丢失,所以引入TNN来替换式(2)中的核范数,得到式(3)。

(3)

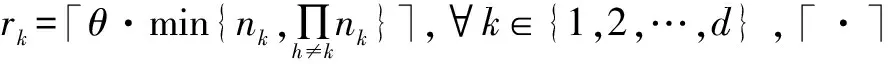
1.4 算法求解

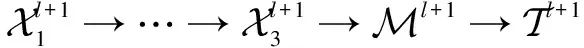
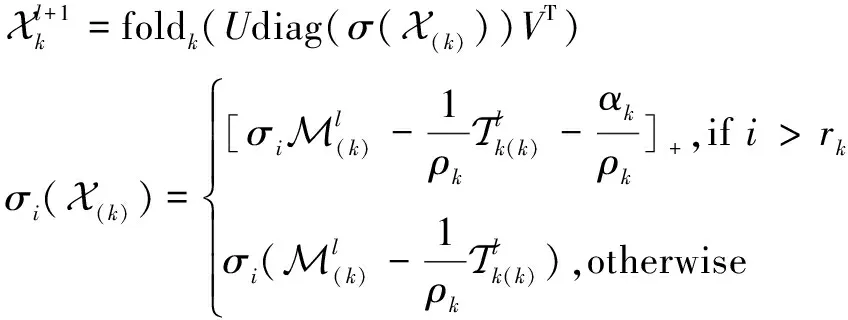
(4)

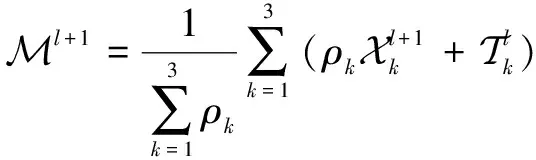
(5)

(6)

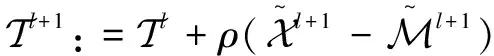
(7)

1.5 瞬时水流量数据时空关系

该文将二维瞬时水流量数据转换成满足“日期块×日期×时间”关系的三阶张量数据,用Y表示转换后含有缺失值的瞬时水流量张量数据,X表示最终填补缺失值后的张量。将Y作为输入,通过张量补全任务式(3)求解X,其本质是张量补全过程。利用算法1中的ADMM将张量补全任务式(3)分解成迭代求解Xk,M,T的三个子问题。其中Xk是X(k)经过基于TNN的奇异值分解处理后重构的张量,k可以取1,2,3,意味着能从不同的方向上提取Xk的各种特征。M用来保留观察信息,然后将这些信息广播到张量Xk中,并对Xk进行迭代更新。T在ADMM中用来进行对偶更新。每次迭代都会通过解Xk得到X,再判断X是否达到收敛条件,若达到则输出,若未达到,则不断迭代更新X。

1.6 基于LRTC-TNN的瞬时水流量数据插值算法

正如图1所示,为了利用LRTC-TNN模型将带有缺失值的瞬时水流量数据插补成完整张量,给出以下预处理步骤:

第一步,依据1.5节的方法通过张量展开和折叠结合奇异值分解的方式将原始瞬时水流量数据调整为具有特定规则的张量结构;

第二步,基于LRTC-TNN模型将张量补全任务式(3)分解为3个子问题,通过迭代收敛求解这些子问题预测缺失水流量数据;

第三步,进行缺失值填补。

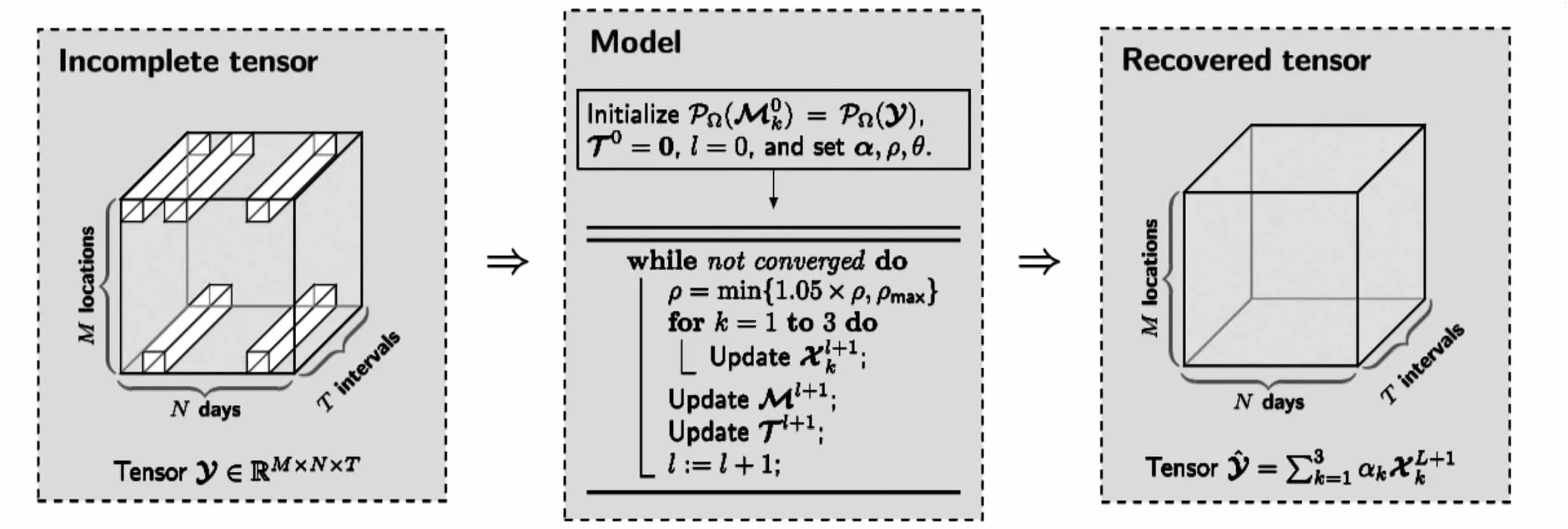
图1 LRTC-TNN模型进行插补的主要过程

该算法的伪码如下:

算法1:基于LRTC-TNN的瞬时水流量数据插值算法。

说明:YD×T:含缺失值的矩阵 XD×T:缺失值被填充后的矩阵

YM×N×T:含缺失值的张量 XM×N×T:最后补全的张量

输入:y

数据关系转换:y→Y

初始化:α,ρ,θ,ε,max_inter

It=0

While true:

ρ=min{ρ×1.05,ρmax}

forkin (1,2,3):

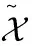
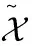
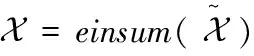
由Y和X计算tol

it++

if(tol<ε)or(it≥max_iter):

break

return X

数据关系转换:X→x

输出:x

2 实 验

2.1 实验概述

在本节中,将传统的均值插补、常用的两种机器学习方法(K近邻和XGBoost)、近期新提出的深度学习方法(GAIN和HyperImpute)以及BTMF(Bayesian Temporal Matrix Factorization, BTMF)[13]、TRMF(Temporal Regularized Matrix Factorization,TRMF)[14]和该文提出的方法应用于瞬时水流量数据缺失值插补问题中。最后利用MAPE(Mean Absolute Percentage Error,MAPE)和RMSE(Root Mean Square Error,RMSE)分数对这些算法进行评估。

2.2 数据集说明

实验中采用的数据集采集于某水厂管道183天从第0时刻开始至第22时刻结束每隔15分钟记录一次的瞬时水流量。每天共记录88个数据项,组成一个样本,即每个样本中有88个特征变量,数据集中0代表缺失值。由于一些不可控因素,采集的数据中有多个样本中存在连续缺失值或独立缺失值。从采集过程可知,该数据具有极强的时间序列数据特性。表1对该数据集进行了简要表示。

表1 瞬时水流量数据集

在实验中,人为地对数据设置缺失率,分别为0.3、0.6、0.8。特别需要说明的是,Jafraste等人在研究[15]中将数据缺失模式分为三类:完全随机缺失(Missing Completely At Random,MCAR)、随机缺失(Missing At Random,MAR)和非随机缺失(Missing Not At Random,MNAR)。目前,大多研究是针对MCAR[16-17]和MAR[18-19]两种模式。该文将数据缺失模式总结为两类,将MCAR和MAR归为一类并记作RM(Random Missing),用以泛指随机出现的独立缺失值,取MNAR中连续缺失形式作为特例,并记作CM(Continuous Missing),表示连续缺失值。

2.3 基线模型

将引入以下基线模型与LRTC-TNN模型进行对比:

·贝叶斯时态矩阵分解(Bayesian Temporal Matrix Factorization,BTMF[13]):2021年Chen X等人将向量自回归(vector autoregressive,VAR)合并到传统的贝叶斯矩阵分解(Bayesian Matrix Factorization,BMF)模型中提出了BTMF模型,通过处理VAR中的系数矩阵识别和解释不同时间因素之间的因果关系,因此BTMF能有效处理时间序列中的缺失值。

·时态正则化矩阵分解(Temporal Regularized Matrix Factorization,TRMF[14]):2016年Rao N等人运用多重自回归过程对潜在的时间因素进行建模,用一个动态模型增强时间平滑性。BTMF和TRMF都是由贝叶斯时间张量分解模型[20]推广得到。

·均值插补:该方法将缺失值用该时刻下其它采集到的可观测数据的平均值进行填充,数据集规模大小对插补性能有直接影响。

·中值插补:该方法将缺失值用该时刻下其它采集到的可观测数据的中值进行填充,插补性能同样受到来自数据集规模大小的直接影响。

·最频繁数值插补:该方法将缺失值用该时刻下其它采集到的可观测数据中出现次数最多的数进行填充。

·K近邻(K Nearest Neighbor,KNN):该方法会参考缺失值附近的可观测数据的k个值,并用这k个值的均值填充缺失值。

·XGBoost(eXtreme Gradient Boosting):对于含有缺失值的特征,通过枚举所有缺失值在当前节点是进入左子树还是右子树来决定缺失值的处理方式。

·HyperImpute[21]:2022年Jarrett等人提出了一种通用的迭代插补框架,用于自适应和自动配置模型及其超参数。基于线性模型、树、XGBoost、CatBoost和神经网络的回归和分类方法对缺失值进行迭代插补,其本质是一种集成学习方法。该方法在大量公共数据集上进行缺失值插补实验并取得了SOTA效果。

·生成对抗插值网络(Generative Adversarial Imputation Networks,GAIN[22]):2018年Yoon等人提出了一种基于GAN模型,通过生成器对缺失值进行估算,利用判别器确定实际观察到哪些成分以及哪些成分被估算,并以提示向量的形式向判别器提供额外信息的缺失值插补模型。

该文对基线模型的选择做出了如下考虑,一方面选取遵循矩阵结构的方法,该类方法多是基于低秩时间矩阵分解的模型,它们的插值估算能充分利用时间信息和数据的低秩性,如BTMF、TRMF。另一方面选取遵循张量结构的方法,此类方法能利用更多维度的信息进行插值估算,如文中方法。最后,还对比了传统方法、基于机器学习的方法和基于神经网络的方法。

2.4 超参数设置

参考文献[8]并结合文中数据集情况,对模型中的超参数进行合理设置。将α1、α2、α3均设置为1/3,用以捕捉模型处理过程中三个关键张量展开的权重。设置学习率参数ρ=10-4,ρ的大小会影响模型的收敛速度,ρ过大会增加学习时的迭代次数从而减慢模型的收敛速度,可能会导致过度学习,ρ过小又会因为迭代次数过少使模型收敛速度过快,可能导致学习不足。设置θ=0.3,θ是一个通用速率参数,又称核范数截断率参数,用于控制输入在按某模式张量展开时的整个截断。θ和ρ的设置直接决定了模型性能。设置ε=10-4,ε是用于求解模型的迭代收敛条件。设置模型最大迭代次数为200。在以上超参均不变的情况下,分别设置缺失率0.3、0.6、0.8用于对模型性能进行评估,同时也可作为对照实验。将183×88的数据集转换成3×61×88的输入张量,即是将二阶张量数据集进行抽象的升维形成三阶张量,使原数据集由1个水厂183天的瞬时水流量记录抽象成3个日期块61天的瞬时水流量记录,虚拟出了一个“日期块”维度,使之符合LRTC-TNN模型的输入层要求。对于BTMF和TRMF中的参数,分别参照了文献[13-14]中实验进行合理设置。将K近邻法中的K值设置为3,XGBoost中参数依照数据集情况合理设置。GAIN和HyperImpute中的参数均由文献[21]中框架自动配置。以上实验在同一随机数种子下进行。

2.5 实验结果分析

由于数据集中的缺失值是完全随机出现的,有些缺失值只单独出现,称为独立缺失值,有些缺失值则相邻出现,称为连续缺失值。鉴于文中方法插值效果在整个数据集上的良好表现且独立缺失值在瞬时水流量数据集中只占0.000 3,该文只对不同缺失率下连续缺失值的样本进行实验,用于说明连续缺失值插补情况,具体参阅图2～图4,横轴表示第几次采集,纵轴表示瞬时水流量,左边面板代表连续缺失值出现在中间时刻样本的插补情况,右边面板代表连续缺失值出现在采集开始时刻样本的插补情况,图中曲线中平行于横轴的线段即为缺失值。可知,随着数据集中缺失率的提高,插值曲线与真实曲线的重叠越来越少,且波动越来越剧烈,意味着随着可用信息的减少,文中方法的插值效果也会变差。其次,还能看到在缺失率低于0.6的情况下,文中方法对连续缺失值的插补效果都比较稳定,无剧烈波动,当缺失率达到0.8的时候,插值曲线在真实曲线附近上下波动剧烈,此时的插值效果已经差强人意。除此之外,右边面板插值曲线与真实曲线的重叠情况在不同的缺失率情况下都要比左边面板好,间接说明了文中方法并不完全依赖之前时间步这一单独因素对缺失值进行插补,还会综合其它维度信息对缺失值进行插补。

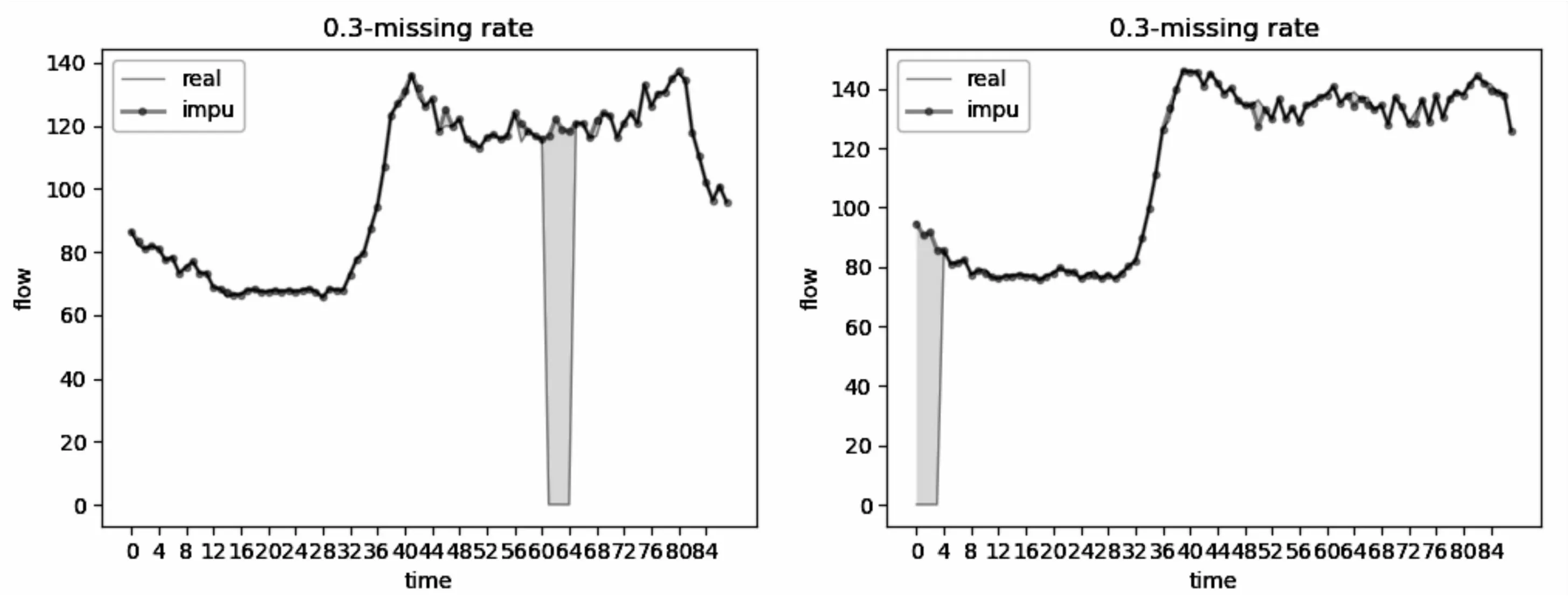
图2 0.3数据缺失率

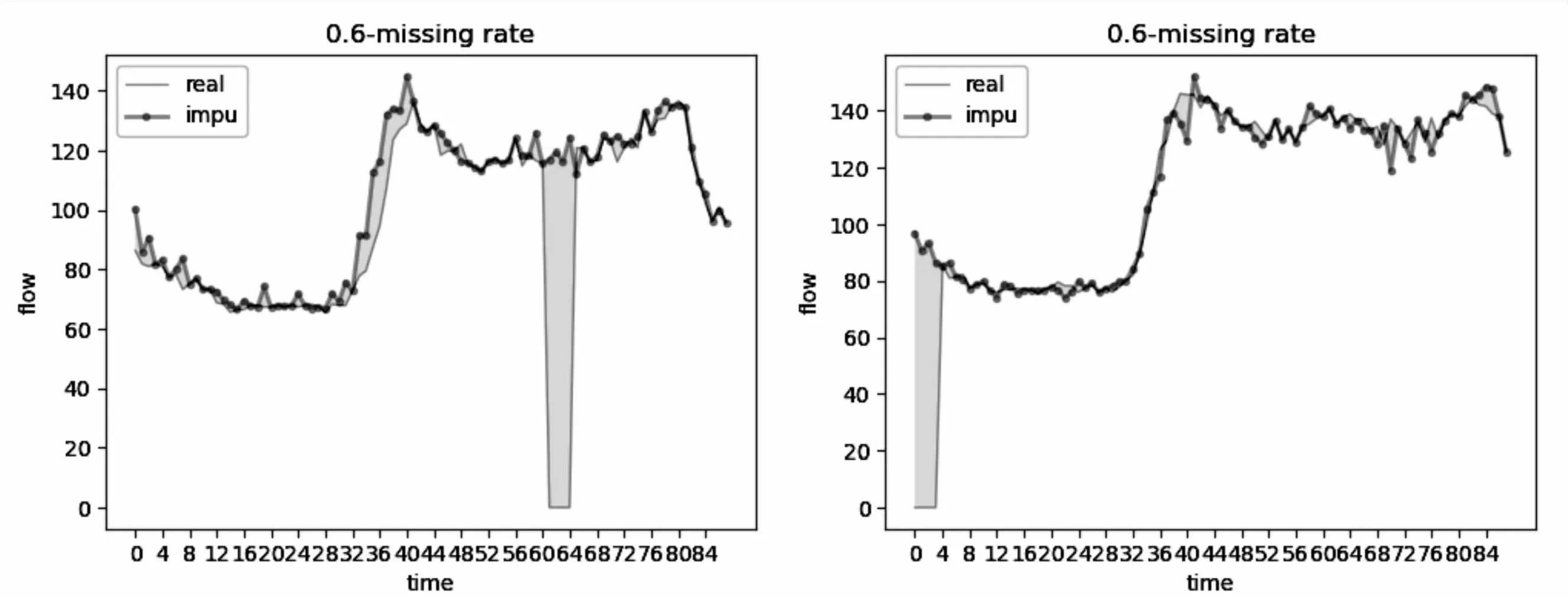
图3 0.6数据缺失率

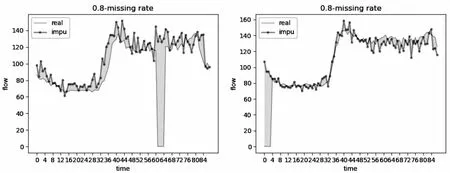
图4 0.8数据缺失率

表2展示了不同缺失率下各算法的MAPE和RMSE值,得分的右上角标代表了性能排名,1为最优。除了传统的均值、中值、最频繁插值方法外,可以了解到其它所有算法的缺失率越高,MAPE和RMSE值也越高,揭示了模型的误差也越大。在缺失率为0.3的时候,可见KNN的MAPE和RMSE值都要比文中方法和基于神经网络方法的低,有更好的性能,但随着缺失率的增大,KNN的各项也急剧变大,性能明显变差,这也符合KNN方法的特点。在不同缺失率下,文中方法的插值性能都能进入前三且接近甚至优于一些基于神经网络方法的SOTA模型。此外,发现传统的缺失值插补方法在不同缺失率下,MAPE和RMSE值都远高于其它方法,且几乎无变化,这也暗示了此类插补方法并不适合瞬时水流量数据的连续缺失值插补任务,下文将不再对其进行讨论。

表2 各模型的表现比较(MAPE/RMSE)

图5中揭示了各插补方法在不同缺失率下MAPE和RMSE值的变化趋势。显然,在不同缺失率下文中方法都有接近基于神经网络方法的先进表现,尤其是在高缺失率下,MAPE和RMSE值都是平稳变化,表现出了与HyperImpute方法同样的稳定性。而TRMF、KNN和XGBoost的各项值会随着缺失率的提高出现剧烈的变化,当缺失率达到0.6的时候,斜率明显增大,各项值的变化幅度急剧变大,在高缺失率下,性能明显变差。与文中方法类似,虽然BTMF在不同缺失率下各项值的变化都较为平稳,但整体而言,MAPE和RMSE值都高于文中方法,性能差于文中方法。另外值得一提的是,文中方法在缺失率为0.3和0.8的时候,各项值都低于GAIN方法,性能略优于GAIN方法,其次,GAIN方法随着缺失率的增加,其斜率明显变大,而文中方法斜率变化却非常小,基本接近SOTA模型HyperImpute方法,这也说明了文中方法具有较强的稳定性。从本质上进行分析,HyperImpute方法是一种网络式的集成学习方法,主要依靠数据驱动,且需人为设置的超参以及网络训练过程中需要更新的参数较多,极易受到超参和数据量大小的影响,而提出的LRTC-TNN方法是一种基于一定数学先验知识构建数学模型解决问题的单一算法,对数据和超参的依赖并不如HyperImpute那般明显。通过实验可知,LRTC-TNN方法性能接近HyperImpute模型性能,也反映了所构建的数学模型的合理性和科学性。

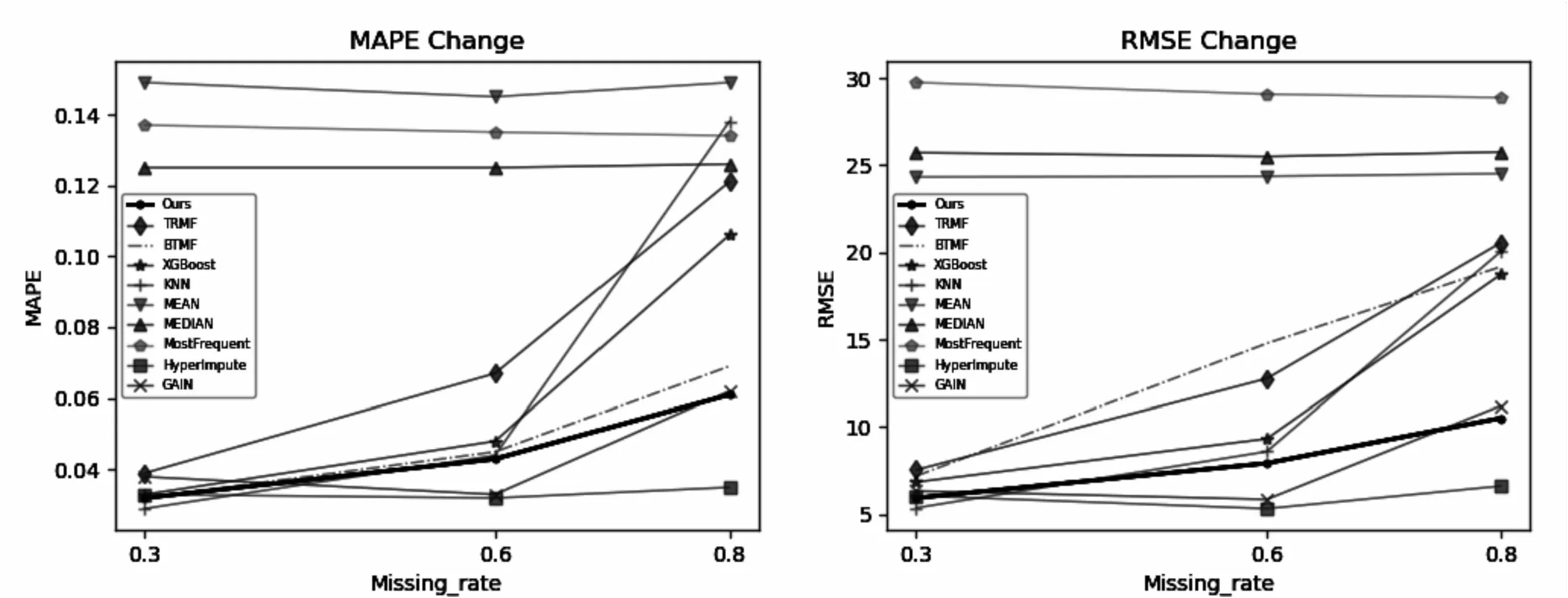
图5 MAPE和RMSE值变化

3 结束语

通过实验展示了含有连续缺失值的瞬时水流量数据在不同缺失率情况下的插补情况,论证了基于LRTC-TNN的瞬时水流量数据插值方法在数据集低缺失率情况下的良好性能,在较高缺失率情况下仍有较强的稳定性,体现在MAPE和RMSE分数随缺失率的提高没有出现强烈波动。基于LRTC-TNN的瞬时水流量数据插值方法在瞬时水流量数据缺失值插补任务中的良好表现也间接说明了对瞬时水流量数据集的低秩假设是合理的且能高效捕捉数据的时间依赖性和特征相关性,进而对缺失值进行有效估算。该方法取得了较好的插值效果,一方面说明了该方法对低维时间序列数据具有很好的兼容性,另一方面也为处理瞬时水流量数据的连续缺失值问题提供了有效方案。