在“模型”中感悟运算一致性

【摘 要】教学“分数除法”时，教师可以通过整体设计“模型”，以多样化的问题模型丰富学生对运算意义的理解；以模型直观探究算法的抽象表达，通过“为什么这样算”的任务驱动，加深学生对算法的形式理解；以模型的多解深化认识，凸显运算本质的内涵，促进学生感受运算一致性。

【关键词】小学数学；模型；运算一致性；分数除法

【中图分类号】G623.5  【文献标志码】A  【文章编号】1005-6009（2023）14-0020-04

【作者简介】孙敬彬，北京市中关村第三小学（北京，101301）教师，高级教师，江苏省数学特级教师。

分数除法在意义上与整数除法、小数除法相同，在方法上颠倒相乘后和分数乘法一致，在算法理解上也有很多如平均分和包含除、商不变规律、分数意义等方面的经验。基于这么多的联系，笔者试着从“模型”的角度来为学生提供支持，在意义、方法、路径等方面进行勾连，借助“模型”设计把运算“高高举起”，通过“模型”感知把一致性“轻轻放下”，从整体的视角发展学生的运算能力。

一、能解决什么问题——以“模型”多样丰富意义的理解

苏教版六上在“分数除法”单元安排了分数除以整数、整数除以分数、分数除以分数这三部分内容。分数除以整数以“平均分”选择素材，整数除以分数、分数除以分数以“包含除”选择素材。受篇幅所限，教材在内容上不可能选择很多。而生活中需要用分数除法解决的实际问题也不多见，所以要多引导学生结合实际生活看到分数除法，感受到分数除法的实际意义，这样他们才会与以前学习的除法进行对接。这样结合实际，从分数的意义、除法的意义的角度多找一些问题模型，进一步促进学生感受分数与除法、比的关系，他们在问题解决中自然会感受到运算意义的一致性。

1.发散提问，让不同问题汇聚

在这个单元的学习中，可以多让学生带着算式回到具体问题情境中，想一想“这道算式还可以解决生活中的什么问题”，引导学生用数学的眼光去看生活，通过提问丰富平均分、包含除等在实际生活中的更多表达，为学生学习分数除法提供更多问题模型。如教学“分数除以整数”时，可以提问：4/5÷3还可以解决生活中的哪些问题？这样发散提问后，班内学生就会汇聚出很多问题：小刚3分钟跑了4/5千米，平均每分钟跑多少千米？我3天读完一本书的4/5，平均每天读这本书的几分之几？用3元能买4/5千克橘子，1元能买多少千克？课桌高4/5米，教室高3米，课桌高相当于教室高的几分之几？……这些不同问题的出现，使原来分数除以整数的单一问题模型变得丰富起来，学生感受到的意义也会更具体，同时为他们解决运算方面的问题提供了更多体验。

2.聚焦设问，把相似问题串联

由于教材中平均分和包含除的模型不断切换，问题情境也不同，问题相关度不是很高，因而单元学习时对分数除法算式的每一次提问都要关注问题情境的延续性，聚焦设问“能提出解决有关路程类的问题吗？”“能解决买东西中的问题吗？”，把发散的提问“串”起来。如在学习“分数除以整数”时，学生提出了“小刚3分钟跑了4/5千米，平均每分钟跑多少千米？”这一问题，到后面的学习中设问让学生跟进，就会有“小刚2/3小时跑了4千米，平均每小时跑多少千米？”“小刚3/10时步行9/10千米，他平均每小时步行多少千米？”等问题出现，这样就把有关速度、时间、路程的问题模型在整个单元中关联起来了。这样“问”出来的问题，能让学生从整体的角度想问题模型，从模型的角度思考除法的意义。

3.反复追问，将关键问题统整

对于学生提出的这些问题，可以经常追问一句：“为什么用除法？”如“3元能买4/5千克的橘子”，既可以提问“1元能买多少千克？”，也可以提问“买1千克需要多少元？”。对于这两个问题，可以适时追问：为什么都用除法？为什么列出的算式不同？学生会从意义的角度解释，或者借助直观图来解释，这能使他们进一步加深对问题模型的认识，丰富对分数除法的意义理解，沟通除法与分数的联系。同时，对于某个问题的反复追问，能帮助学生从问题模型中生长出算法和算理的理解，生长出解决实际问题的能力。如引导学生探究“4米长的绳子，每2/3米剪一段，可以剪多少段？”“一根绳子用去2/3，正好用去4米，这根绳子长多少米？”這两个问题“为什么都用除法”，能促进他们关注部分与整体之间的变化。

二、为什么这样算——以“模型”直观探究算法的表达

分数除法的计算方法是“甲数除以乙数（不为0），等于甲数乘乙数的倒数”，从形式上看就是颠倒相乘，学生很容易知道，但要想说清楚“为什么这样算”并不容易。整体设计时就可以以“为什么这样算”为大任务，充分放手让学生想办法说清楚算理，并借助直观模型让其感受到运算在本质上的联系、算法上的相通。

1.有“整”有“分”，让算法一致清晰化

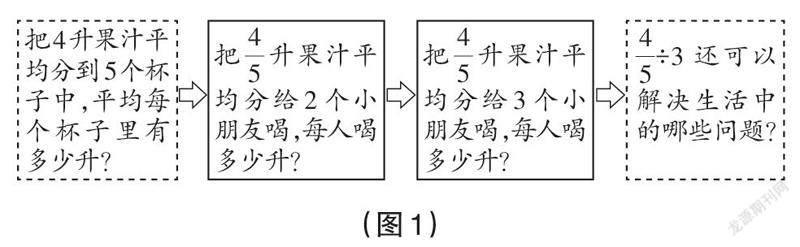
“整数除法可以表示为分数的形式”，这等价于“除以一个不为0的整数等于乘这个数的倒数”，即a÷b=a×1/b=a/b（b≠0）。因此，在整体设计“分数除法”单元的教学时，可以在第一课时植入一个“整数除以整数”的情境，让情境更有连续性。这样基于分数与除法的关系，学生能感受到分数除以整数的算法与整数除以整数是一致的。具体的问题串设计如下页图1所示。这样设计也能让模型整体“组团”，整数除以整数可以用实物模型“4升果汁，5个杯子”；“4/5÷2”可以用面积模型；“4/5÷3”可以用面积模型，也可以用线段模型。

学生在“把4升果汁平均分到5个杯子中”的过程中，看见了“4升的1/5”的算式是“4×1/5”，看见了每杯果汁的数量是“1/5+1/5+1/5+1/5”，就是“4×1/5”，因而问题解决过程中就有了“4÷5=4×1/5=4/5（升）”，虽然是蜻蜓点水，但单位累加的感觉轻轻浮现，颠倒相乘的认识清清楚楚。

2.有“理”有“据”，让算法表达直观化

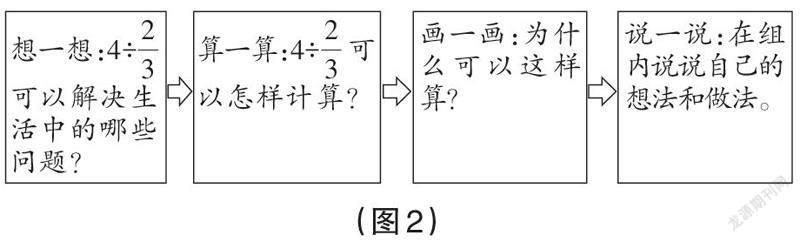
学习“分数除以整数”以后，学生就能类推出分数除法的算法了。下面的除法学习围绕“怎样算”“为什么这样算”来展开，可以放手让学生为“法”说“理”，让算法从一个个模型中直观呈现，使学生真正理解算法。实践中可以设计如图2所示的任务链，引导学生自己先进行研究，然后结合不同模型从不同角度说理，进一步丰富他们对算法的理解。

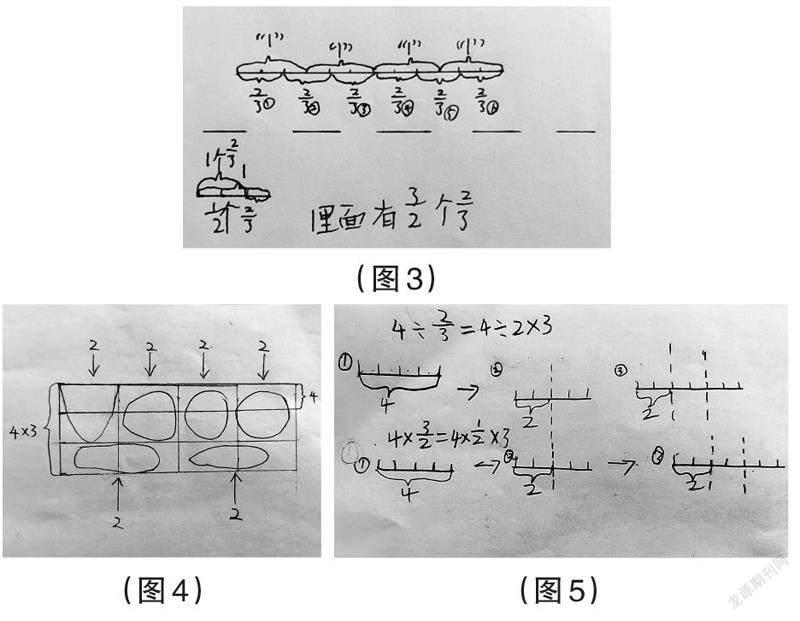
生1：把“1”平均分成3份，我先找到1个2/3，剩下的那份正好是2/3的一半，也就是1/2个2/3，这样就能看出1里面有3/2个2/3，所以4里面有（4×3/2）个2/3，4÷2/3=4×3/2。（如图3）

生2：我是把“1”平均分成3份后，发现“4”里共有这样的12份，2/3是这样的两份，所以就有4×3÷2，根据分数与除法的关系可以写成4×3/2，所以4÷2/3=4×3/2。（如图4）

生3：2/3可以写成2÷3，4÷2/3=4÷（2÷3）=4÷2×3，而4×3/2=4×1/2×3，所以4÷2/3=4×3/2。（如图5）

可见，在说清“为什么这样算”的过程中，学生能感受到分数除法与以前学习的运算在实质上是一致的，而且能想办法说清楚为什么这样算也是一个推理验证的过程，经历这样的过程，学生对算法的理解便走向了对其中计数单位以及计数单位个数运算的理解。相信当出现如下算法时，学生也能很快结合具体模型来解释它们背后的道理：4÷2/3=（3×4/3）÷2/3=12÷2=6；4÷2/3=（4×3/2）÷（2/3×3/2）=6÷1=6；4÷2/3=（4×3）÷（2/3×3）=12÷2=6。

三、還可以怎样想——以“模型”多解感悟运算的本质

从整体的角度对“分数除法”单元进行模型设计，能使学生对一些问题与算法的理解更直观具体，也有利于凸显运算的本质。一是一个算式会有不同的问题模型，让学生有更多机会从意义的角度理解算法；二是不同直观模型在解释算法上又会各有不同，即便是同一个直观模型，不同学生的表达也会有所不同。教师教学时要多通过对比引导学生变换角度思考“还可以怎样想”，从中发现更多联系和运算的本质内涵。这样用好直观模型，很多原有经验、方法都会在汇聚后进行有效提升并实现统一。

1.一“图”多“义”，解释中实现方法统一

在画直观图探究算法的过程中，笔者发现很多问题在直观表达时有一致的地方，即很多问题情境表达出来时可能是相同的一幅图。在探究算法的过程中，结合直观图适时追问“还可以怎样想”，有利于学生从模型的角度把一类问题提取出来，让问题模型与计算方法在一幅直观图中得到统一。图6呈现的是4/5÷3的计算过程，其实也是分数乘法中4/5×1/3的计算过程。这样借助直观图的多种理解，不仅能使学生看到分数除法与分数乘法在算法上的一致性，也能把单位的运算凸显出来，对算法和算理进行了统一。

2.一“式”多“图”，对比中凸显运算本质

学生在探究算法时会想到很多方法，这些方法看似模型不一样，理解不一样，但背后蕴含的道理可能是一样的。让学生通过对比“还可以怎样想”，能使他们发现运算本质上的一致性。学生对一致性的理解也会反过来促进他们在算法上的求同以及对通法的探寻，从而使他们从模型直观走向推理验证。如教学9/10÷1/10时，教师引导学生对比图7和图8，并适时追问“还可以想到哪些”，能使学生发现分数除法和整数、小数除法计算在想法上是相通的，在方法上是一致的。有了这些认识，学生也会慢慢从直观模型中发现一些本质的东西，从更宽广的视角感受到可以计数单位相除、计数单位个数相除，最后再把商相乘的道理。

学习“分数除法”以后，教师还可以把问题模型在三节课中的“样子”呈现出来，通过一“模”多“样”，让学生从整体的角度对同一问题模型有整体认识，对算法的形成有整体感知，如三节课中的路程类问题（如图9）。

学生从中不仅能想到问题是如何直观呈现的，还能想到4/5÷3、4÷2×3、9/10÷3×10的计算方法是相通的，道理是一致的。回看“分数除法”单元的学习，还能感受到运算方法似曾相识，运算过程殊途同归。这些理解对学生感悟运算一致性有好处，还能促进他们将其迁移到解决分数实际问题的学习中去。