移动云中支持健康数据共享的可追责大属性多授权CP－ABE 方案

唐靖蕾， 巫朝霞

（新疆财经大学 统计与数据科学学院， 乌鲁木齐 830012）

0 引言

移动健康医疗（mHealth）云集合了广泛的新兴技术［1］，如可穿戴医疗传感器、云计算、通信技术。移动健康系统使患者能够通过各种可穿戴或可植入的医疗物联网传感器监测和收集人体信息，并通过移动设备集成个人健康记录（PHR）。 然后，PHR 将通过5G 网络上传到云服务器，以节省移动设备的有限存储容量。 由于PHR 数据包含各种隐私信息，持有者希望实施访问控制策略以确保PHR 数据只能由授权用户访问。 然而，如果采用传统的访问控制技术，则由于云服务器无法完全信任或仅支持粗粒度访问策略，PHR 数据安全将会受到损害。

为了解决上述问题，基于密文策略属性的加密（CP－ABE）［2］被提出，该技术可以同时实现细粒度访问控制和数据安全。 在CP－ABE 中，密文中加入访问策略，用户的私钥由属性集创建。 只有当用户的属性集与嵌入的访问策略匹配时，解密才会成功。尽管传统的CP－ABE 机制可以保护敏感PHR 数据的安全性和隐私性，防止泄露给未经授权的用户，但在mHealth 中广泛部署和应用之前，仍有2 个主要的挑战性问题需要进行探讨与研究。

首先，传统的ABE 的目标是实现“一对多”的加密，但单一权限和属性的分散管理问题是其实现的瓶颈，因此需要在分布式系统中使用多权限ABE设计。 针对这些问题，Chase［3］提出了最初的多权威ABE （MA－ABE）方案，其中存在一个中央权威（CA）和多个属性权威（AA），每个用户都用唯一的全局标识符（gid）标记。 随后，MA－ABE 出现了多种增强和扩展。 Lewko 等学者［4］提出了去中心化多授权机构CP－ABE 方案，该方案在随机预言机模型下被证明是完全安全的。 Zhang 等学者［5］提出了基于匿名认证的个人健康记录的MA－ABE，在用户与云服务器之间进行认证时隐藏用户的身份和属性。

然而，在实际中移动健康云需要对属性和用户进行动态扩容，因此大属性ABE 比小属性ABE 更实用。 在小属性框架中，所选安全参数的属性集被限制为多项式大小。 这一限制将对移动健康云中的动态实际应用造成瓶颈。 在大型属性集系统中，属性域可以设为指数级大。 Rouselakis 等学者［6］在素数阶双线性群中构造了一个大属性MA－ABE 方案，该方案比复合阶双线性群效率更高。 Huang［7］基于素数阶双线性群，提出了第一个无密钥滥用的可撤销大属性去中心化MA－ABE，该方案支持属性、用户和权限的动态扩展，但其访问结构存在暴露风险。

其次，文献［3－7］中的方案只考虑多授权机构的问题，但未能考虑恶意用户追踪问责等问题，为实现叛徒可追踪，需防止合法用户密钥滥用。 Liu 等学者［8］提供了一个高度表达的白盒跟踪方案，支持任何单调访问策略。 Zhou 等学者［9］提出支持白盒跟踪和撤销的MA－ABE，应用于电子医疗云计算系统的多层隐私保护，只实现数据用户身份的隐私，但系统需要大量的计算消耗。

本文在文献［6］的基础上，结合追踪算法［10］提出了一种面向移动健康支持大属性多授权机构的可追踪CP－ABE 方案，该方案的特点如下：

（1）支持属性、用户和权限的动态扩容，适用于动态移动健康系统中大规模的多领域协作。

（2）根据追踪算法可以检验出参与泄露解密密钥的恶意用户，从而提高了效率，并且不需要存储开销。

（3）线性秘密共享方案提供了按需求频繁地修改密文访问策略的灵活性，允许对数据所有者进行研究细粒度控制。

1 背景知识

1.1 双线性映射

设G0、G1、GT都是阶为素数p的乘法循环群，双线性映射e：G0× G1→GT具备以下3 个特性：

（1）双线性：对于∀a，b∈Zp，∀u∈G0，∀v∈G1，有e(ua，vb)＝e(u，v)ab，当G0＝G1时称为对称双线性映射。

（2）非退化性：∃u，v∈G0，使得e（u，v）≠1。

（3）可计算性：对于∀u，v∈G0，可以有效计算e（u，v）。

1.2 线性秘密共享方案（LSSS）

假设A是一个单调的访问结构，M是一个l × k的矩阵，ρ是一个行标记函数：将M中的行i映射为A中的属性att（i）。 一个LSSS 由2 个多项式时间的算法组成：

（1）共享算法（（M，ρ），s）：该算法输入（M，ρ）和一个秘密值s∈ℤp，并随机选取元r2，r3，…，rn∈ℤp，设定向量。 该算法输出一个集合作为s的共享份额，其中是矩阵M的第i行，共享份额λρ（i）属于属性ρ（i）。

（2）重构算法（（M，ρ），L）： 该算法输入（M，ρ） 和一个授权属性集合L∈A。 该算法输出一个秘密重构系数集合使得。 因此有。

1.3 困难假设

判 定 性 q － BDHE2 （ q － Decisional Parallel Bilinear Diffie－Hellman Exponent 2， q－DPBDHE2）

假设［6］，即：

给定G和GT为素数阶p的双线性群，g为G的一个生成元。e：G×G→GT是一个定义在G上的双线性映射。 随机选取GT，给定， 并 要 求 从 （D，R） 区 分 （D，e（g，g）saq＋1）。 算法A用求解G 群中的q－DPBDHE2问 题 的 优 势：｜Pr［A（D，e（g，g）saq＋1）＝0］－Pr［A（D，R）＝0］｜≥ε。

如果不存在概率多项式时间算法以不可忽略的优势解决判定性q－BDHE2 问题，则称q－BDHE2 问题是困难的。

2 方案构造

2.1 系统模型

本次研究的方案构造模型如图1 所示。 方案中主要实体包括：属性授权机构（Attribute Authority，AA）、移动健康云服务提供商（mHealth Cloud Service Provider，mCSP）、数据持有者（Data Owner，DO）、数据用户（Data User，DU）。

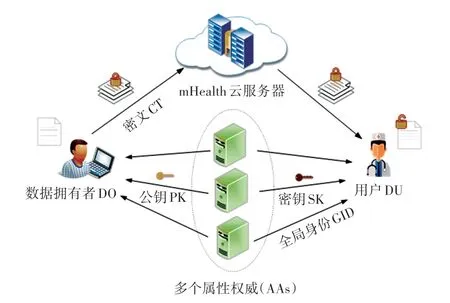
图1 本文方案构成Fig. 1 The scheme proposed in the paper

对个人健康记录（PHR）数据共享模型中的实体介绍如下：

（1）AA 是属性授权机构，每个属性权威拥有并管理一个属性集合，各个属性权威所管理的属性集合不存在交集。

（2）mCSP 是系统中可提供强大的存储能力和通信能力的云服务商，主要负责系统中PHR 存储、管理密文数据和关键词搜索等服务。

（3）DO 是指数据的持有者，通过移动或可穿戴物联网设备收集和集成PHR，数据持有者希望将其数据外包到mCSP 提供给云中的客户。

（4）DU 是指访问云中数据的用户，例如医生、营养师、研究人员等。 每个数据用户都有自己的私钥与自己的属性集相关联。

2.2 具体方案

在本方案的构造中，U是属性集合，Uθ是权威机构集合，对于每个属性i∈U由特定的权威θ控制，一个公共可计算函数T：U→Uθ将属性i映射到权威θ，对于l × n访问矩阵A，ρ将其行映射到属性，函数δ·( )＝T（ρ（·）） 将其行映射给权威机构。假设G是素数阶p的双线性群，e：G × G→GT是一个双线性映射。 对此拟展开研究分述如下。

（1） Global Setup（λ） →GP。 算法中，首先选择阶为素数p的双线性群，g是G的生成元，e：G×G→GT是G双线性映射，然后将选择哈希函数H：G将用户身份映射到G群的元素，哈希函数F：U→G 将用户属性映射到群G的元素，全局公共参数为：

（2） Authority Setup（GP） →PKθ，MSKθ。 每个权威θ∈Uθ选择3 个随机指数，并计算公钥和私钥SKθ＝｛αθ，yθ，aθ}。 身份标识表L被初始化为空表。

（3）Encrypt（GP，M， A，｛PKθ｝） →CT。 给出明文M，访问策略（A，ρ），相关属性公钥｛PKθ｝，算法首先选择2 个随机向量v ＝（s，v2，…，vn）T，ω ＝对于每个计算λx＝Ax·v，ωx＝Ax·ω，其中Ax是A的第x行，算法选择随机数rx∈Zp，计算密文CT 如下：

（4）KeyGen（GP，ID，S， ｛MSKθ｝） →SK。 输入全局参数GP，身份ID，属性集S，以及相关权威的主密钥｛MSKθ｝，对于每个属性i∈S， 如果T（i）＝θ，权威机构θ选择2 个随机值t∈Zp， 计算K1＝。

属性集S的GID私钥：SKu＝｛K1，K2，T1，T2｝，算法把（K2，ID） 放入身份信息表L，其中K2关联用户身份ID并作为追踪参数。

（5）Decrypt（GP，CT，SK） →M。 给定公共参数GP，密钥SKu，密文CT，I⊂ { 1 ，2，…，l} 定义为I ＝{x：ρ（x） ∈S}，如果S不满足访问策略（A，ρ），输出⊥。 否则对于每个x∈I，算法首先计算Dx＝；然后，计算常数使＝（1，0，…，0），计算得出；最后，可以将消息恢复为M ＝C0／e（g，g）s。

（6）Key Sanity Check（GP，SKu） →1 or 0。 输入公共参数GP和私钥SKu， 算法将检查解密密钥是否满足完整性检查，该检查由3 个部分组成：

如果解密密钥SKu满足式①、②、③，则可以通过密钥完整性检查，算法输出1；否则，算法输出0。

（7）Trace（GP， ｛PKθ｝，SKu，L） →ID。 该算法由权威机构执行。 如果解密密钥SKu不能通过密钥完整性检查，算法中止，输出⊥。 如果SK是正常结构的，则算法在表L中查找K2：如果能够在T中找到K2，则算法输出相应的id，否则算法输出⊥，表示该私钥未被系统分发。

3 方案分析

3.1 正确性证明

由用户执行Decrypt（） 算法，当用户的属性满足访问机构的设定，才能正确解密出密文，本文方案的正确性证明如下：

如果属性集合S满足访问策略（A，ρ），计算常数使（1，0，…，0）， 然后得到0。 因此，

3.2 安全性证明

定理1 证明了所提出的方案如同文献［6］方案一样是静态安全的。

定理1在q－DPBDHE2 假设下，提出的具体方案在随机预言模型中是静态安全的。

证明假设存在一个概率多项式时间敌手B，该A能以不可忽略的优势ε攻破所提出的方案，那么可以构建一个模拟器B，以同样的优势ε攻破文献［8］方案。 用C表示文献［8］方案的挑战者。 接下来展开研究分述如下。

（1）全局设置。B从C获取全局参数GP ＝｛p，G，g，H，F，U，Uθ，T｝，然后将其传递给敌手A。

（2）敌手查询。 敌手A静态地发出多项式有限数量的查询。

（3）授权机构的公钥查询。 敌手A提交一组没有腐败的属性集合Nθ∈Uθ和一组腐败属性集合Cθ∈Uθ，Nθ∩Cθ＝Ø。 在文献［8］方案中创建其对应的公钥为对于θ∈Cθ，敌手A选择2个随机数，并将本文中腐败权威的公钥设为。

（4）用户的属性密钥查询。 敌手A根据用户自身 的id创建密钥SKu， 并提交一串序列表示敌手查询与用户IDj相关属性集合Sj的密钥。

（5）加密查询。 敌手A提交访问结构（A，ρ），和2 个同等长度明文m0，m1。 设SCθ是腐败权威控制的所用属性的集合，j∈［m］，要求集合SCθ∪Sj不满足（A，ρ）。

（6）挑战者回复。C随机选择b∈0，1，对查询的响应如下：

在接收到敌手的查询后，模拟器B发送Cθ，Nθ，给C请求提供相应的文献［8］里的公钥、密钥、挑战密文。 然后C返回公钥私钥， 挑战密文CT′如下：

其中，x ＝1，2，…，l，然后B以如下方式回复查询。

（7）授权机构的公钥回复。 对于每个权威θn∈Nθ，B随 机 选 择， 假 设 公 钥PKθ＝。

（8）用户的密钥回复。j∈［m］，i∈Sj，B随机选择r， 设 置计 算K1，i＝选择另一个随机值r，再次尝试回复，最后B将密钥设置为：

（9）加密回复。 对于x∈｛1，2，…，l｝，B计算，B设定挑战密文CT ＝（C0，，最后B发送公钥密钥和挑战密文CT给敌手A。

在猜测阶段中，A输出一个猜测b′∈｛0，1｝，如果b′＝b，则A赢得游戏。

如果A有优势AdvA（λ）＝ε在破坏本文方案时，B可以以相同的优势AdvA（λ）＝ε破坏文献［6］方案，参见方案文献［6］。 在q－DPBDHE2 假设下，文献［6］方案在随机预言模型中是静态安全的，因此本文提出的方案也是静态安全的。

3.3 性能分析

本方案与文献［6］、文献［11］、文献［12］进行了性能比较，主要是从方案的访问结构，可追踪性等6个方面，分别对相关多授权机构方案进行对比分析。其中，符号及对应含义见表1。 在本次研究的效率比较中，只考虑成本高的操作。

表1 符号及对应含义Tab. 1 Symbols and corresponding meanings

表2 给出了相关多授权机构方案的特征比较。从表2 可以看出，文献［11］采用阈值访问结构，与本文方案采用的LSSS 访问结构相比灵活性更差。文献［12］采用合数阶群，而本文方案基于素数阶群上的构造，从而具有更好的执行效率。 从整体功能上看，本文提出的方案同时支持多个授权机构、大属性以及恶意用户追踪，因此，该方案相比文献［6］的方案具有更丰富的功能。

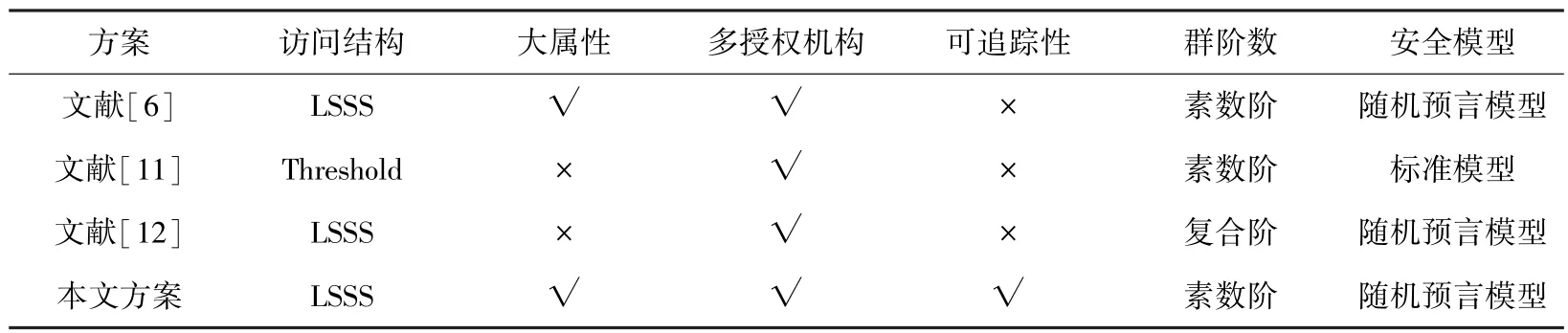
表2 方案功能特征对比Tab. 2 Comparison of the functional characteristics of the schemes

计算复杂度比较见表3。 从表3 可以看出，对比文献［6］，本文方案为实现可追踪的功能，多进行了一个指数运算，即在群G1上指数运算增加了1，但总体的加密、解密时间和文献［6］方案的差距不大。 本文方案的加密时间比文献［11］方案的更优，文献［11］在加密阶段使用多次双线性配对运算，导致加密时间增加。 本文方案和文献［6］、文献［12］都是基于LSSS 提出的，但只有本文和文献［6］方案支持大属性，因此属性全集在系统建立阶段不需要具体化，属性个数可以无限增多，在加密、解密上都能快速运算。 在解密开销方面，本文方案还远远优于文献［12］方案。

表3 计算复杂度比较Tab. 3 Computational complexity comparison

为了衡量本文方案与文献［6］、文献［11］中所提方案的加解密开销，本方案所有仿真实验都在配置为Intel（R）Core（TM）i5－11300H＠ 3.10 GHz，RAM 为16 GB 的Windows10 系统笔记本电脑上的虚拟机运行，虚拟机平台：VMware ® Workstation 16Pro，操 作 系 统 为Ubuntu20. 04。 本 实 验 利 用Python 语言进行编译，算法仿真中双线性对的选择基于超奇异对称椭圆曲线组（SS512），仿真结果取50 次测试结果的平均值。

不同方案加密时间比较如图2 所示，不同方案解密时间比较如图3 所示。 由图2、图3 可知，加密、解密随着属性的数量呈线性增长。 从图2 可以看出，所提方案的加密时间与文献［6］方案几乎相同，都低于文献［11］方案。 在图3 中，很容易看出，提出的方案比文献［8］方案需要更多的解密时间，但明显低于文献［11］方案的解密开销。

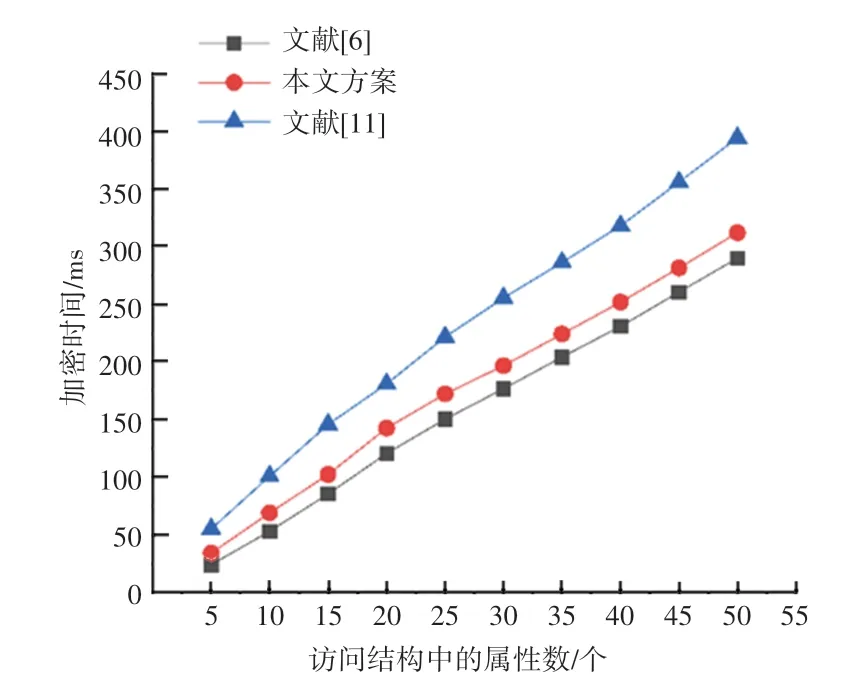
图2 不同方案加密时间比较Fig. 2 Comparison of encryption time of different schemes

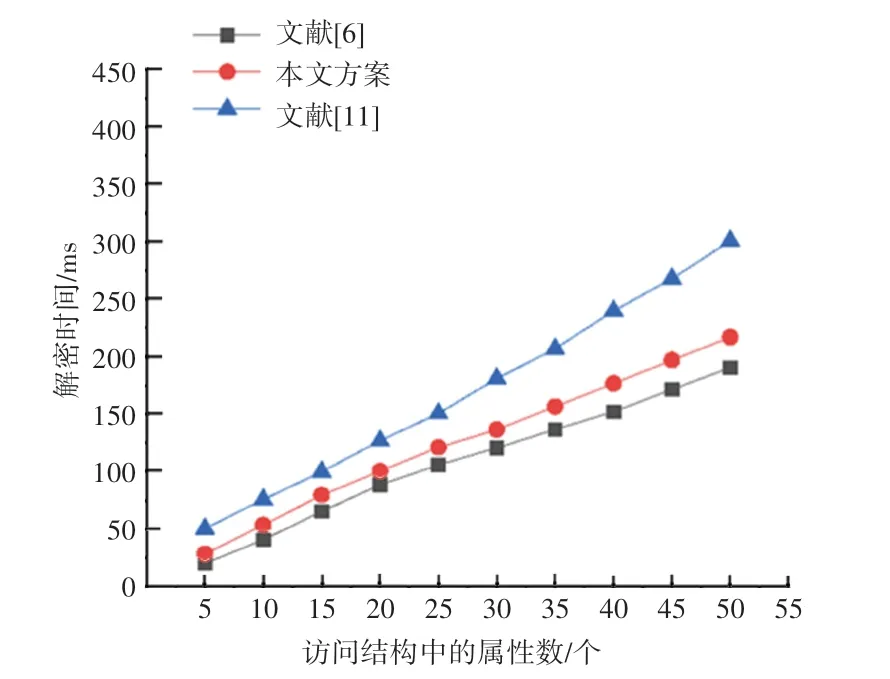
图3 不同方案解密时间比较Fig. 3 Comparison of decryption time of different schemes

4 结束语

本文根据移动健康的应用提出一种大属性域可追责的多权威机构属性加密方案，方案减少了中央权威的负荷和风险；采用LSSS 访问结构，使访问策略具有高表达力和高拓展性；在q－DPBDHE2 假设下，该方案在随机预言模型中是静态安全的。 实验结果和性能分析显示，本文方案在加解密效率上优于对比方案，且在功能上更丰富。