大规模有向网络的K可控性研究
2023-05-17李晓丽
曾 涛,李晓丽
(东华大学 a.信息科学与技术学院, b.数字化纺织服装技术教育部工程研究中心, 上海 201620)
各种大规模网络系统无处不在,大到覆盖全国的国家电力网络和Internet网,小到人体内的神经网络,甚至是生活中的人际关系网络。这些网络系统具有维度高、关联复杂,以及不确定性等特征[1-2]。如何给网络系统中某些节点施加控制作用使网络达到预期的状态,这是广大学者一直研究的方向。随着科技发展,计算机的计算能力大大提高,其成为分析复杂网络的强大工具,可进一步推进网络可控性的研究。

由传统的能控性理论可知,线性系统可控的充分必要条件是系统能控性判别矩阵满秩。Mortazavian[13]首先提出“K-controllability”的概念,“K-controllability”是一个满足能控性判别矩阵的秩条件的指标。为了描述这个指标,Li等[14]提出结构能控性指数K来描述这个指标,且给出“K-controllability”的一个充分条件,并对该条件充分性进行证明,但是并没有证明“K-controllability”的必要性,也没有对大规模网络和真实网络进行仿真。一个网络是否可控决定于网络中是否存在扩张,扩张是网络中产生控制输入需求点。Chung等[15]提出一个基于扩张的框架,该框架能够清楚地了解哪些节点可能是网络的输入节点,同时该框架还可以分析网络在扰动下的可控性。Chen等[16]从能量的角度指出,当驱动节点到目标节点的路径距离最小时,控制能量是最佳的,这表明网络的结构能控指数K越小,网络的控制能量最佳。一个大规模网络系统中,给系统的哪些节点添加输入可以使系统可控,在控制输入下系统可以分解什么样的子系统,以及可控时的控制长度,这些都是需要研究的问题。
本文的研究重点在于针对一个给定的大规模有向网络系统,从系统的控制性能出发,提出一个K可控定理将大规模网络分解为许多个拥有仙人掌结构的子系统,对系统的结构能控性指数K进行分析讨论,并对该定理进行充分必要性证明。为验证该定理的可行性,设计了一个K可控算法,对大规模网络和真实网络进行仿真,验证K可控算法的有效性。
1 可控性基础理论
1.1 匹配概念和增广路径
定义1给定一个有向图对应的二分图G=(V,E)中,V是G的顶点集,E是G的边集,M=(VM,EM)是G的一个子图,M的边集EM中的任意两条边都不包括相同的顶点,M是G一个匹配。
定义2在二分图G=(V,E)中,包含边数最多的匹配称为该二分图G的最大匹配[7]。
定义3在二分图G=(V,E)中,以未匹配的节点为起点,另一个未匹配的节点为终点。依次按照未匹配边、已匹配边、未匹配边形成的交替路径称为增广路径。
定义4起点和终点重合的一条有向路径称为环。
1.2 仙人掌结构
对于一个拥有N个状态节点和M个控制输入的时不变网络系统,如式(1)所示。
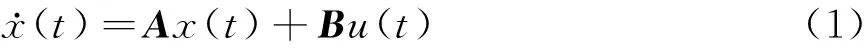
式中:x(t)=(x1(t),x2(t),…,xN(t))T表示在固定时间t下的状态向量;A为N×N维系统矩阵,用来描述节点之间的关联关系和连接强度;u(t)为固定时间t下的控制输入;B为一个N×M维输入矩阵,表示M个控制输入和N个状态节点之间的关系。


对应的有向图称为芽,如图1(b)所示。
定义5一个单输入仙人掌结构由一条“茎”和若干个“芽”按照一定的结构组成,记为G,如图1(c)所示。

图1 仙人掌结构图Fig.1 Cactus structure diagram
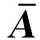

(1)系统每个节点都输入可达并且满足,如式(2)所示。

(2)系统对应的拓扑有向图可以由一个仙人掌结构张成。

1.3 结构能控性指数K
引理2(Kalman秩判据[17]):系统(1)完全可控的充要条件为能控性判别矩阵
C=[B,AB,…,AK-1B,AKB,…,AN-1B]
(3)
满足:
rank(C)=N
事实上,对于已知(A,B),可能存在矩阵:
Q=[B,AB,…,AKB]
(4)
使得
rank(Q)=N
由此给出结构能控性指数的概念。
定义6若系统(A,B)满足式(5)和(6)两种情况时可控,则系统(A,B)可控,且系统的能控性指数为K。
rank([B,AB,…,AKB])=N
(5)
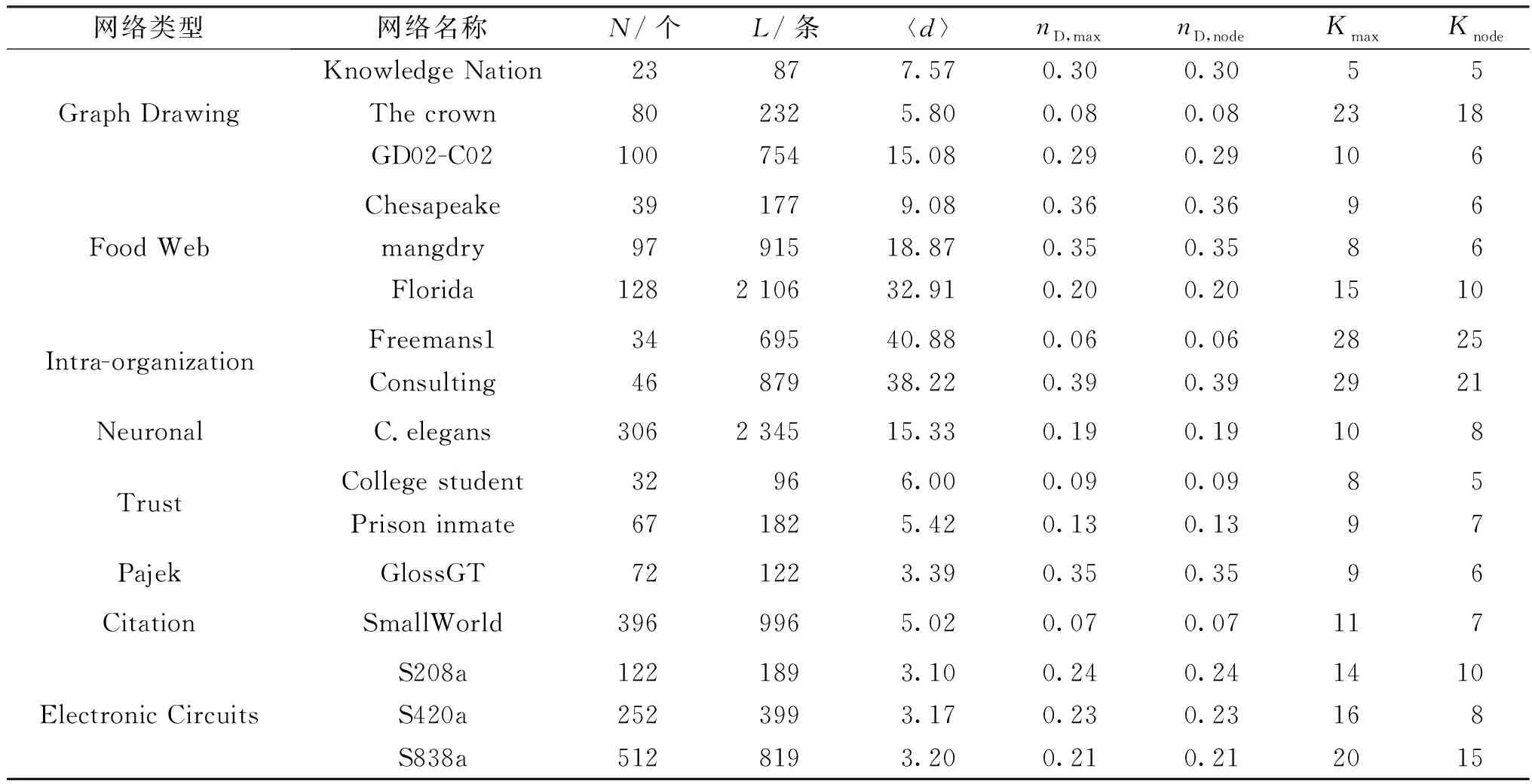
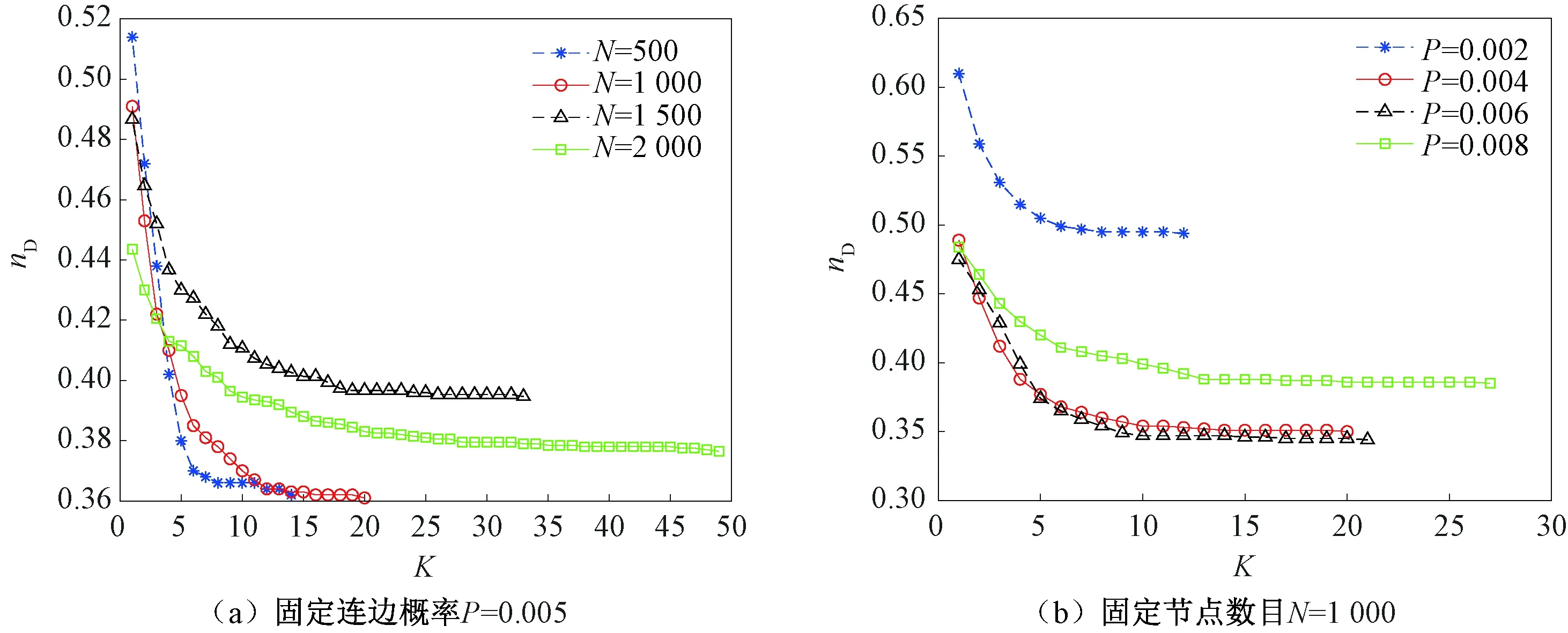
rank([B,AB,…,AK-1B]) (6) 式(7)和(8)中的K≤N,即结构能控性指数K不超过N。结构能控性指数K的物理意义表示从网络系统的控制节点出发通过K次的信息传递可以影响到所有节点,即网络达到可控状态,因此称为K可控。 引理4网络系统(A,B)对应的拓扑有向图G=G1∪G2∪…∪GS,G1,G2…,GS是不相邻的子图,每一个子网络Gi对应的结构能控性指数为Ki,那么网络G的结构能控性指数如式(9)所示。 K=max{Ki,…,KS} (9) 证明:G由不相邻的S个子图G1,…,GS组成,则以下等式成立: 然后能推出 所以,Q=[B,AB,…,AKB]可以被描述为 因此,系统G的能控性指数对应于子网络图Gi([Ai]Ni×Ni,[Bi]Ni×1,),Gi的能控性指数为Ki,显然有 所有的1≤i≤S都满足式(10)和(11)。因此,以上过程证明K=max{K1,K2,…,KS}。结合引理3和引理4,可以提出K可控的充分必要条件。 max{K1,…,KM}=K 步骤1:置集合M为空。 步骤2:找出一条新的增广路径P,通过异或操作获得更大匹配的集合M′,用M′代替原来的M。 步骤4:初始化控制链集合为S1={},存储每一条控制链中所有节点的集合为S1_k={},控制环集合S2={},存储每一个控制环中所有节点的集合为S2_k={},k=1。 步骤5:随机查找未在S1中并且入度为0的点vi(1≤i≤N),令S1_k=S1_k∪{vi}。 步骤6:从vi出发寻找下一个可达节点vj,若存在vj则形成链路vi→vj,令S1_k=S1_k∪{vj}。继续从vj出发寻找,直到找不到可达节点时停止。将找到的控制链vi→vj→…→vn存入集合S1_k中且k=k+1。 步骤7:重复步骤5、6,直到不存在入度为0的节点为止。 步骤8:随机选取不在S1和S2中的剩余节点vs(1≤i≤N),令S2_k=S2_k∪{vs},重复步骤6寻找控制环vs→vk→…→vs,并将控制环存入集合S2-k中,令S2=S2∪{S2-k}。直到所有节点都遍历完停止。 如果希望能控性指数K的数值不至于过大,也就是控制链过长的问题,可以通过对矩阵维度进行控制,将矩阵进行再分块使得最大维度变小,最终使结构能控性指数变小,但会增加控制节点。 通过步骤1可以把矩阵简化成以下形式: 利用K可控算法对大规模随机网络进行仿真,表1为仿真结果。N为网络节点的个数,L为网络的边的总数,〈d〉为随机网络的平均度。令nD=ND/N来表示网络系统的控制输入情况,其中ND为控制节点。nD,max为最大匹配算法下得到的值,nD,node为文本提供的算法下得到的值。Kmax是最大匹配算法[5]下的结构能控性指数K值(控制链路的最大长度),Knode为K可控算法下的结构能控性指数K值。 表1 随机网络仿真结果Table 1 Simulation results for random networks 由表1可以看出,K可控算法和最大匹配算法拥有相同的最少驱动节点,使得网络K可控,显然两种算法的原理都是寻找增广路径,但是K可控算法在此基础上加入了仙人掌结构。同时,K可控算法在相同网络和相同驱动节点下,拥有更小的结构能控性指数K值,即控制链路相对更短,控制速度更快。针对不同规模的随机网络,当网络的平均度〈d〉值相差不大时,nD的值变化不大。由此说明最小控制输入与网络的平均度相关。对不同的真实网络进行仿真(见表2),所有的真实网络数据集来源于文献[4]。从表2可以看出,K可控算法拥有和最大匹配算法一样的最少驱动节点,网络可控时的结构能控性指数K值更小。同时可以看出网络平均度〈d〉相差较大时nD的值差距也较大,验证了网络的平均度决定网络的最小控制输入。同时验证K可控算法的可行性,为真实网络驱动节点的选取和控制性能研究提供一定的参考价值。 表2 真实网络仿真结果Table 2 Simulation results for real networks 利用限制结构能控性指数K值,观察K值和最小控制输入的关系(见图2),P表示节点之间的连边概率,N表示节点数量。其中:图2(a)为P=0.005时对不同节点数量N的网络仿真结果;图2(b)为N=1 000时对不同连边概率P的网络仿真结果。由图2的仿真结果可知,在同一网络中,K值与最小控制输nD呈负相关,并且K值越大,最小控制输入变化越小。由此说明:在网络系统中,长的控制链总是占少数,短的控制链占大多数,因此当K值较小时,断开的控制链越多,增加的驱动节点就越多;K值越小,驱动节点的增加速度越快。由图2(b)可知,在相同节点数量下,连边概率越大,最小控制输入越小。文献[12]研究表明,当连边的概率P<0.006时,最小控制输入随着P的增大而减少。同时连边概率越大,结构能控性指数K值越大。基于以上规律,在真实网络中应该根据实际情况选择合适的K值和控制节点。 图2 K值与最小控制输入的关系Fig.2 Relationship between K value and minimum control input 本文为研究大规模有向网络系统的控制性能,将结构能控性指数K作为其控制性能的指标,提出K可控定理将大规模网络系统分解成独立可控的“仙人掌”系统,从而得到系统的结构能控性指数K和驱动节点集。基于该定理提出K可控算法,利用计算机对大规模随机网络和真实网络进行仿真,结果验证了K可控定理的有效性。此外,通过限制子矩阵的维度来控制能控性指数K的大小,同时明确不同K值与最小控制输入之间的关系,为真实网络驱动节点的选取提供参考。
2 主要结论


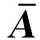


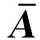

3 算法设计

3.1 K可控算法步骤


3.2 案例分析


4 仿真结果分析

5 结 语
