基于小波包分析的高压输电线路故障测距方法

广东创成建设监理咨询有限公司 邹庚

1 小波包法的基本原理及基函数的选择

1.1 小波分析基本原理

高压输电线在运行过程中会出现瞬态量，按瞬时的频段划分为工作暂态成分和高频暂态成分，而在高频瞬态成分的频段范围更广。傅立叶分析是目前常用的频谱解析法，但其仅适合于振幅波动较为平稳，且频率较为稳定的信号。无论是傅立叶转换还是其改良的方法，都属于比较常规的信号处理方式，从数学运算的角度考虑，傅立叶转换技术自身也有一些问题，即当对广域的数据进行分析时，会忽视一些子带的数据，这对数据中的有效特征值产生干扰。与常规的傅立叶转换相比，小波方法可以很好地解决其在处理过程中的问题。小波解析具有时间窗口和频窗的特性，可以在任何时段中抽取任何一个频段的数据，利用小波方法可以快速地将故障后所生成的各种复杂的暂态数据进行提取，因而小波方法被用于故障信号的处理。

1.2 小波包分析基函数的选择

与傅立叶转换比较，小波转换有着诸多优点，小波转换中可以选取的小波基较多，而且可以自行构建，但是傅立叶转换仅使用单一的基本功能，因此小波转换的适应性更强。在小波转换中如何选取基函数，目前尚无一个通用的理论准则，一般都是依据具体的小波函数属性、信号特性和所做的分析决定。在进行小波转换时，若所选的基本功能波形与所选的基本波型相似，则将具有接近基本功能的部分放大，而非接近的部分会受到压制。小波与待加工的信号之间的相似性一般表现为小波系数，小波幅值与小波信号相似，系数越高越相似。通过对Morlet 小波的分析和实践证明，Morlet 算法在信号分类、图像识别和特征抽取等领域具有较好的性能。在检测物质的损害时，常用的是样条小波。通常采用Shannon 小波来解微分方程，Haar 或Daubechies经常被用来进行数据分析和数据处理。

Daubechies 小波（或简称dbN） 仅有dbl（haar小波），dbN小波有着许多优点，例如正交性、紧支集、连续小波转换、小波分析等优点，使得dbN 小波在工程上有着广阔的应用前景。本文通过对线路失效后的故障进行小波分析，对其进行时、频率的分析，从而得到不稳定的信号中的突变部分、瞬时部分和奇异部分。在选取小波基时，必须考虑到小波基的选取问题，并依据故障后的故障信号特点，选取具有良好的频率域性的小波基，通过比较和比较，最后选取db4小波进行故障诊断与处理。

2 利用小波包法进行能量特性的提取

2.1 小波包法中的能量特性提取原则

利用小波包法对离散型x(t)进行J级的分解，可以获得具有j= 1,2,...,2J特征的多个波段的Dt。小波包能值为一种小波包的全因子之和。

式中，n为细节系数内的点数。

总小波包能量是：

相对小波包能量是：

由上面所推导的小波包能值可以由该方程求出。

2.2 时频域故障特征量选择与选取

小波分析具有很好的时间域局域性，能够反映出信号的时间-频率特征。从故障信号中抽取出的信号，采用50kHz 的取样频率，并选取3 个相位电流iA、iB、iC和零序电流i0。利用db4 小波方法，把iA、iB、iC和零序电流i0实现8 级分解，并将其进行了分析，得出了其中的高频特征信号因子d1(k)～d8(k)和低频近似的信号因子d9(k)。

三相电流的小波能是典型的三相子。故障特征向量为T1，按照（4）式，可以得到三相的电流的频率EA、EB、EC以及归一化值eA、eB、eC，并将eδ的数值与所设置的门限进行标记，若eδ大于所设置的数值，则视为1，若小于设置的数值则视为0。构成了一个失效的特征值T1=[eA，eB，eC]。

电源的电压相差为δ。零序电流中的小波能为失效的特征量T2。将零序i0中的低频率功率E0与三相电流对应，也就是将门限值设为1或0，从而构成一个特征量。

式中，d09(k)为i0小波分解后的低频近似信号系数。

该方法的故障特征值T3～T10是三相电流的子波因子的标准值。计算iA、iB、iC中每个小波因子标准差σ(dAJ)、σ(dBJ)和σ(dCJ)，j= 1，2，...，8，按照（6）式对该频率小波的标准差进行规范化，并判定该规格化的数值，若σδ大于设置的阈值，就需要将其量化为1，若不能量化为0，由此构成了一个失效特征量[σA(j)，σB(j)，σC(j)]。

式中， max(σ(dJ)) 和min(σ(dJ)) 是σ(dAJ)、σ(dBJ)和σ(dCJ)中的最大值和最小值。

通过对10 种不同类型的故障特性矢量进行组合，可以获得一种基于T=[T1,T2,...,T10]T的高电压传输线的故障类型。

3 试验结果与分析

3.1 试验准备

以某区域的一条高压输电线为试验对象，采用ATP-EMTP 建立一条线路的两个非同步，然后将该方法的结果导入MATLAB，通过MATLAB的超强运算功能，进行数据的分析、处理和校核。

该部分为320kV高压电线，利用分布参数建模建立线路侧模拟的参数，电缆长度500km，单元正序阻抗0.0127 +j0.268Ω/km，其中M和N侧的正序阻抗分别选定为0.725 +j40.24Ω 和2.341 +j134.13Ω，两侧的零序阻抗分别为0.2342 +j13.42Ω和0.7805 +j44.71Ω，线路正序阻抗和零序阻抗值分别为0.0127 +j0.268Ω/km 和0.2729 +j0.84Ω/km，零序分布电容值为-99.3 × 10F/km，正序分布电容-81.367 × 10F/km。M、N两端的电压幅脚相位角度有30°的偏差，在两侧安装了一个电流测试模块，用来设定故障。该电路的工作频率为0.03s，截止1s，并按ATP模拟的参数设定0～0.15s的取样时限。本文所示为三种典型的高压输电线的失效模拟。提供了一个单相接地（A 相接地短路）、两相短路（BC相短路）、两相接地（BC相接短路）、三相短路（ABC三相短路）。仿真系统模型如图1所示。

图1 仿真系统模型

3.2 算法仿真与解析

模拟系统中设置小波包相关的参数周期以1000个周期为单位进行。定义A-G、BC-G、BC、ABC分别是单相短路、双相接地、相间短路、三相短路。

3.2.1 过渡电阻分析

在假设高电压传输线的失效长度为220km 时，得到了在各种转换电阻下的失效间距的相关误差，各种失效电阻器的仿真结果见表1，该模拟模式的相对偏差小于0.1，满足了技术规范的需要。表1显示了该方法在各种失效情况下的模拟计算。在这里Em∧En= 30°、同一短路转换电阻器Rf= 20Ω，接地-短路转换电阻器Rg= 10Ω。

表1 各种失效电阻器的仿真结果

各种故障点下的仿真结果见表2，发现在不同的失效情况下，小波分析的测距速度与短路长度的关系不大。

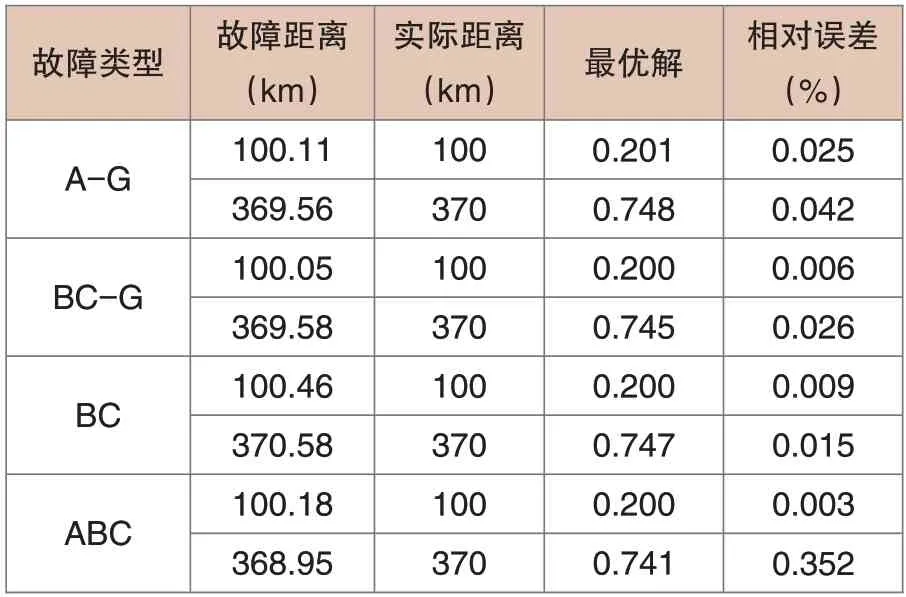
表2 各种故障点下的仿真结果

3.2.2 不同步角分析

A-G型故障时各种角度仿真见表3。

表3 A-G型故障时各种角度仿真

不一致的步角度是指在同一基准相量的情况下，对各线之间的资料进行比较。对M、N 两种不同情况下，进行了模拟分析。设定220km 的故障范围，并用Rg= 10Ω 进行了短路的转换。通过对比，发现在两种情况下，该方法得到的模拟结果几乎没有差别，说明两种方法之间的不同步没有引起太大的影响，相反，随着步角的增大，其相对偏差也随之增大，直到45°时，相移角度越大，其相对偏差越大，180°时的相对偏差为0.007383。

3.2.3 集中参数线路分析

不同模型下的仿真结果见表4，表4为在中心参量和分布参量两种情况下的模拟。设置220km的失效范围。通过模拟计算，得出在集中参数模式下，模拟的错误值比分散参数模式要高。应用分布参数模式可以更好地反映实际线路的实际失效位置，特别是在有分布电容的超高压输电系统时，应用该模型在测量准确率方面更有优越性。

表4 不同模型下的仿真结果

4 结语

通过对高压输电线路的实时监测，可以有效地降低巡线的运行成本，使高压输电线路的运行更加可靠。本文将小波包方法应用于电力系统的故障特征矢量抽取中，并将10 个故障的特征矢量结合起来，获得一种基于特征矢量的高电压传输线的故障类型。利用ATP 软件对高压输电线的短路进行模拟，并利用MATLAB 对非同步线进行小波包法的分析和计算，表明小波包法在不受系统阻抗、过渡电阻、步角等影响的情况下，具有很高的识别精度，具有一定的实用性。