基于门限聚合签名的区块链预言机数据传输模型
2023-05-16郭灵贝夏玉洁
刘 炜, 郭灵贝, 夏玉洁, 佘 维, 田 钊
(1.郑州大学 网络空间安全学院 河南 郑州 450002; 2.郑州市区块链与数据智能重点实验室 河南 郑州 450002; 3.郑州大学 互联网医疗与健康服务河南省协同创新中心 河南 郑州 450007)
0 引言
区块链具有去中心化、时序数据、集体维护、不可篡改、可编程和安全可信等特点[1-2],在医疗[3]、人工智能[4]、大数据[5]、货币加密[6]等领域有着广阔的应用前景。而在实际应用中,数据不仅需要从区块链上获取,还需要从链下的外部网络获取。来源于区块链外部的数据会实时更新,但由于网络延迟、节点处理速度等影响,每个节点获取的并不是同一时刻的数据,无法确保多个节点最终执行结果的一致性[7]。为了保证区块链系统中节点数据的一致性,其舍弃了外部动态数据获取的需求,变成一个封闭的、确定性的沙箱环境。在这个环境中,链上的数据都是被动得到的(通过交易的形式输入),智能合约本身无法主动获取链外互联网数据[8]。因此,使用预言机来连接区块链与现实世界[9]。预言机的主要工作就是收集数据并向智能合约提供输入,通过签名引入关于外部世界状态的信息,从而允许确定的智能合约对不确定的外部世界作出反应。预言机具有不可篡改、服务稳定、可审计等特点,并具有经济激励机制以保证运行的动力[10]。
目前,国内外学者对预言机如何解决区块链内外数据互通的问题展开了深入研究。文献[11]提出的Chainlink是第一个去中心化的预言机解决方案,主要提供用于帮助智能合约访问关键链外资源、网站API和传统银行账户支付的预言机服务,但是这种预言机方案数据聚合成本高,可拓展性差。文献[12]提出一种基于投票来决定查询真假的去中心化预言机方案,用户通过放置一定数量的金钱赌注来回答查询,根据预言机的计算报告结果,评估用户的行为进行奖励和惩罚,但是此方案复杂度高,且导致激励机制分配不均。文献[13]提出一种基于区块链和可信预言机的物联网数据分散访问控制系统,使用预言机作为远程用户和物联网数据主机的网关,通过智能合约计算并记录所有预言机的平均信誉分数,但是此方案通过信誉评分来选择预言机,容易产生高分预言机垄断行为,并且数据的存储成本较高。文献[14]提出一种使用Intel推出的SGX指令集扩展的分布式预言机方案,利用SGX和TLS来保证通信数据的完整性,该方案虽然使用了多个预言机来支持数据的可靠性,但过于依赖对硬件的安全部署。文献[15]提出基于应用程序特定知识引擎的预言机实现方案,利用该引擎从多个权威网站智能地收集、清理和分析数据,使得预言机获取的信息来自多个数据源,但是不能为预言机返回的数据提供真实性证明,且不能确保信息的准确性和隐私性。文献[16]提出基于聚合签名的区块链预言机方案,采用多个预言机获取数据来避免单点故障,并使用BLS聚合签名降低存储成本,但是预言机与智能合约之间的交互过程复杂且烦琐,消耗大量的gas值。文献[17]提出一个基于投票的区块链互操作性预言机方案,使用基于BLS阈值签名的链外聚合机制,将一个预言机节点划分为一个聚合器和多个验证器,并生成一个分布式私钥来共同决定请求结果,此方案虽然降低了一定的gas成本消耗,但并没有同时考虑时间效率的提升。
为了在节省成本的同时实现链上链下数据的快速准确互通,本文提出一种基于门限聚合签名的区块链预言机数据传输模型,依据Schnorr门限聚合签名耗时少、效率高的特点,使用多个预言机从多种外部互联网数据源收集信息,设置积分制选举出可信预言机来聚合签名和传输正确数据。结果表明,所提模型减少了数据上链所需要消耗的gas成本,采用Schnorr门限聚合签名提高了签名的时间效率,且保证了上链数据的正确性和可靠性。
1 相关知识
1.1 Schnorr协议
Schnorr机制[18]是一种基于离散对数难题的知识证明机制。Schnorr签名算法是线性的,可以进行签名累加,生成一个最终签名,且只需要验证一次。具体包括以下步骤。
1) 选择素数p和q,使得q是p-1的素因子。
2) 选择整数a,使aq=1(modp),a、p、q构成全局公钥参数,在用户组内的每个用户都可以取此值。
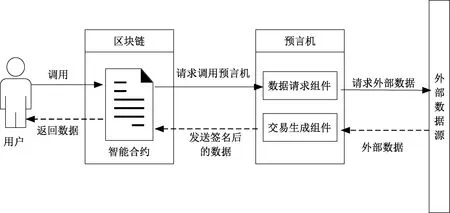
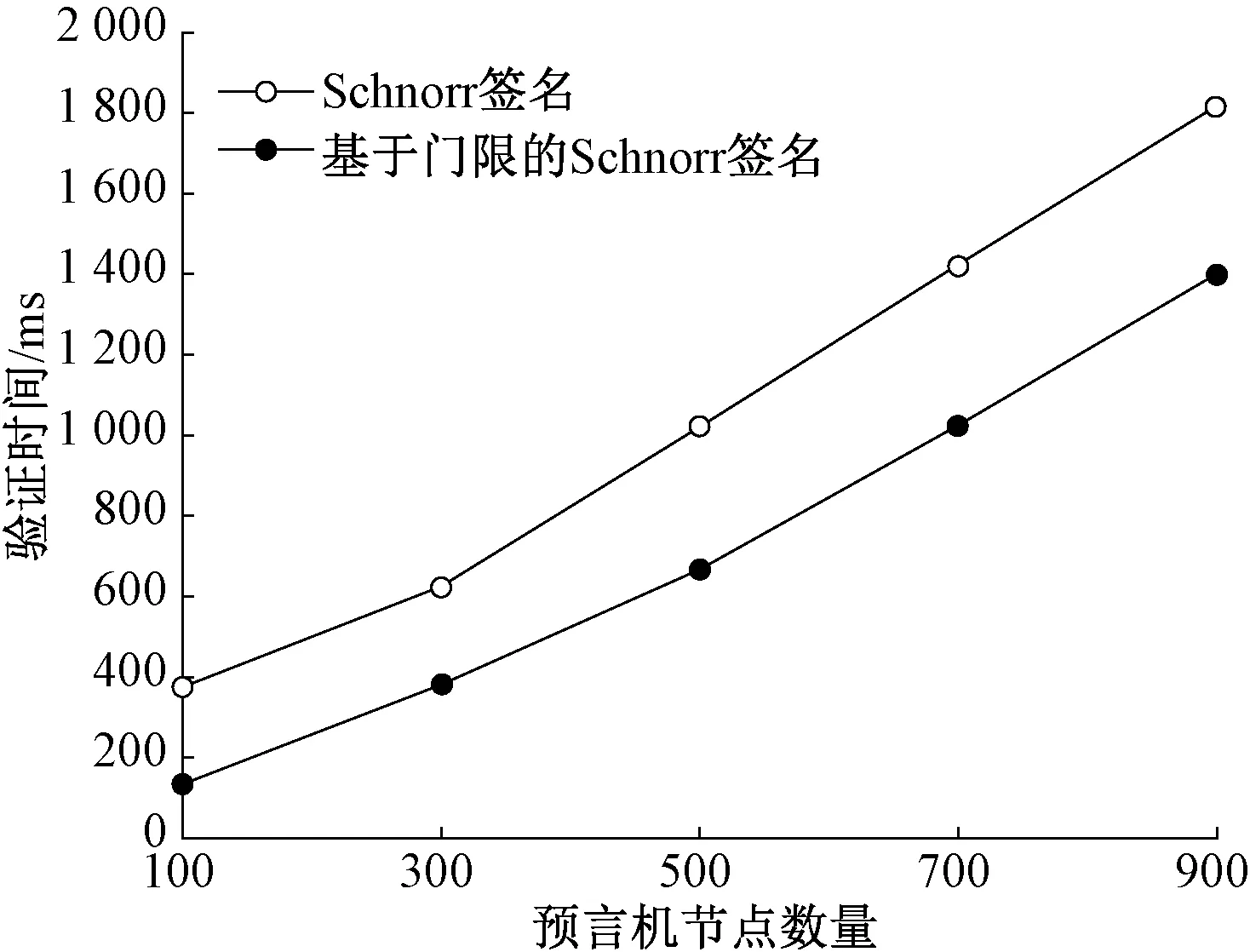
3) 选择随机整数sk,0 4) 计算v=a-sk(modp),作为用户的公钥。 5) 选择随机整数r,0 6) 将x附在消息后面一起计算Hash值e,e=H(M|x)。 7) 计算s=(r+sk*e)(modq),签名值为(e,s)对。 利用Schnorr协议可以聚合的特性把多个预言机的签名进行聚合上链。 (k,n)门限秘密共享方案是把一个秘密分成若干秘密份额,分给n个参与者掌管,在这些参与者中,k个(k≤n)或k个以上的参与者所构成的子集可以合作重构这个秘密[19]。 1.2.1子密钥生成 分享者随机选取k-1个随机数,记为a1,a2,…,ak-1。构造多项式 F(x)=[S+a1x1+a2x2+…+ak-1xk-1](modp), (1) 其中:S为密钥;p为素数。分享者随机选取n个互不相等的非零元素x,分别为x1,x2,…,xn(公开),计算出F(x1),F(x2),…,F(xn),将(xi,F(xi))分别分配给这n个参与者保管,xi是公开的,F(xi)作为子密钥不公开。 1.2.2恢复密钥 构造多项式 (2) 其中:F(xi)为第i个人的子密钥;xi为分享者随机选取的n个不相等的x。取x=0,代入k组(xi,F(xi)),可以求解出F(0),也就是主密钥S。式(2)的多项式为式(1)的变形。将门限秘密共享加入Schnorr签名中,利用门限秘密共享原理从收到的每个预言机签名中的子密钥恢复出群体的私钥。 预言机作为区块链的一个独立模块或第三方服务,与执行引擎进行交互,支持从外部源到区块链系统的数据访问、验证和传输,同时也是基于区块链架构的重要组件[20]。预言机代理机制如图1所示。 图1 预言机代理机制Figure 1 Oracle agent mechanism 预言机只负责数据的可信获取,不直接参与交易的执行。用户通过调用预言机服务接口,告知区块链执行引擎将要执行一笔含预言机服务的交易。执行引擎通过内部通信组件,将用户请求外部数据源的信息转发给预言机模块,如一个Web数据请求,包含HttpRequestHeader、HttpRequestBody等信息。预言机在收到服务请求后,向外部数据源发起数据获取请求,拿到数据后利用交易生成器产生一笔新的内部回调交易,对其进行签名,并将这笔回调交易发给区块链智能合约。 区块链是一个封闭的系统环境,部署预言机可以用来连接链上智能合约与链下数据,使用户能够轻松获取链下数据且能够进行通信和传输。其中,用户是指区块链上开发的DAPP中对链下实时数据的需求者。为了保证数据的正确性和可靠性,提高数据上链的时间效率,防止恶意预言机节点故意传输错误信息,提出一种基于门限聚合签名的区块链预言机数据传输模型。该模型采用多个预言机对链下多种互联网数据源进行数据采集,以防止只用一个预言机发生的宕机和作恶事件,每个预言机都可以从链下外部网络中不同的数据源获取数据。预言机获取数据如图2所示。 图2 预言机获取数据Figure 2 Oracle to obtain data 2.1.2密钥生成 设sk作为群体的私钥,群组O={Oracle1,Oracle2,…,Oraclen},群体大小为n,门限值为t(t f(x)=f0+f1x+f2x2+…+ft-1xt-1(modq), (3) 其中:f1,f2,…,ft-1表示随机数;q表示大素数;f0=f(0)=sk作为群体私钥被n个群组成员共享。x1,x2,…,xn表示n个互不相同的非零元素,分发者将(x1,f(x1)),(x2,f(x2)),…,(xn,f(xn))作为子秘密分发给群组中n个节点Oracle1,Oracle2,…,Oraclen,其中x1,x2,…,xn公开,f(xi)即为每个节点的私钥ski。 2.1.3群体私钥的恢复 (t,n)门限群系统中想要恢复出群体私钥sk,只需要任何t个签名者O1,O2,…,On通过Lagrange内插法重构多项式, (4) 其中:f(xi)表示第i个预言机的私钥ski;x1,x2,…,xn表示n个互不相同的非零元素;t表示门限值。由式(4)可得 2.1.4签名过程 具体签名过程如下。 1)Oraclei选随机数ki,计算Wi=aki,公钥Qi=a-ski(modp),并把Wi、Qi发送给签名合成者。 3) 各签名者有随机数ki,并交换公钥和随机数,计算出x=aki(modp),该过程和待签名消息m无关,将x附在数据信息后面一起计算Hash值e,e=H(m|x)。对数据信息m的签名为 si=ki+skiβiH(m|x)(modq), (5) 其中:si表示签名;ki表示随机数;ski表示签名者的私钥。将(m,si,e,IDi)发送给签名合成者。 5) 链上智能合约收到签名合成者发送的数据和签名后,利用群体公钥进行签名验证, asQe=W, (6) 其中:a表示系统公开参数;s,e表示群体签名对;Q表示群体公钥;W表示系统参数。等式成立则验证通过,将正确数据和签名传送给用户智能合约,然后对发送正确和错误数据的预言机进行积分值的更新。对传送正确数据信息的预言机积分值加1,传送错误数据信息的预言机积分值减1,并对发送错误数据信息的预言机设置5 ms时间延迟包。 基于门限聚合签名的预言机数据传输模型架构如图3所示。假设系统中恶意节点数f不超过群体总数的1/3,设门限值t=f+1。首先,用户通过网络请求用户智能合约,调用链下的预言机获取所需的外部数据;其次,将积分值最高者选为签名聚合预言机,多个预言机通过链下API获取外部数据源;最后,每个预言机收集所获得的数据信息,并各自进行签名,发送收集到的数据和签名给签名聚合预言机。 签名聚合预言机接收数据时首先对签名进行身份验证,然后在收到t(t 模型的具体流程如下。 1) 用户请求链下数据。链上用户触发用户智能合约,请求获取所需的链下实时数据。 2) 调用预言机获取链下数据。用户智能合约调用预言机接口发起查询请求,收集用户需要的链下数据。 3) 预言机获取链下数据。每个预言机接收到用户智能合约消息后,向多个外部数据源获取数据,并用私钥ski对数据信息m进行签名,发给签名聚合预言机。 图3 基于门限聚合签名的预言机数据传输模型架构Figure 3 Oracle data transmission model architecture based on threshold aggregation signature 4) 预言机发送数据和签名。每个预言机都设置积分数值位,用来记录节点的积分值(初始值为0,每发送一次正确数据积分值加1),选出积分值最高的节点,让它成为签名聚合预言机。预言机将获取到的链下数据和签名(m,si,e,IDi)发送给签名聚合预言机。 6) 预言机智能合约调用用户智能合约。预言机智能合约对发送来的群体签名和数据进行验证,若验证正确,则发送正确数据和群体签名给用户智能合约。对发送正确数据的预言机积分值加1,对发送错误数据的预言机积分值减1并设置5 ms时间延时包,使恶意预言机发送数据的时间变长,以尽可能保证先接收到的数据是正常预言机发送的正确数据,从而节约时间成本。 7) 用户智能合约将数据返回给用户。预言机智能合约触发用户智能合约后,用户智能合约接收到数据和群体签名,随后将数据返回给用户,用户收到所需的链下实时数据。 验证:e=H(m|x′)。 所以x′=x,H(m|x′)=H(m|x),说明当e=H(m|x′),代表e=H(m|x),即签名者的签名是正确的。 3.1.2群体签名验证 在签名合成者合成门限签名后,将签名和数据发送给智能合约,智能合约对门限签名进行验证,确保数据的真实性和可靠性。 验证:asQe=W。 所以asQe=asa-sk*e=as-sk*e=aK=W。又因a已知,W已知,公钥Q已知,故验证了asQe=W成立,证明群体门限签名是正确的。 3.2.1实验环境 智能合约在Remix上编译,环境选择Injected Web3链接metamask的账户,将智能合约在本地Ganache私有链上部署。使用Java语言对BLS和Schnorr签名进行模拟仿真,实验环境为Intel I7-9300,内存为16 GB,操作系统为window10,采用JDK1.8,实验结果使用Matlab进行数据处理与分析。 3.2.2与BLS聚合签名的验证时间对比分析 为了验证本文提出的基于Schnorr的门限聚合签名的可行性,设计了基于Schnorr的门限聚合签名算法实验,在同等硬件环境下与文献[16]中提出的基于BLS聚合签名的预言机方案进行对比。在10个预言机节点的情况下,对输入的32 B字符串数据进行签名,分别对BLS聚合签名和Schnorr门限聚合签名的验证时间进行15次测试,对比结果如表1所示。 表1 Schnorr门限聚合签名与BLS聚合签名的验证时间对比Table 1 Comparison of verification time between Schnorr threshold aggregation signature and BLS aggregation signature 单位:ms 由表1可以计算得出,Schnorr门限聚合签名的平均验证时间为23.67 ms,而BLS聚合签名的平均验证时间为887.67 ms。因此,在同等实验环境下,本文提出的基于Schnorr的门限聚合签名效率更高,时间成本更低。这是由于BLS聚合签名的双线性映射构造复杂,提升了计算成本,而Schnorr门限聚合签名利用椭圆曲线上加法同态加密的思想,在计算性能上占有明显的优势。 3.2.3加入门限机制前后的验证时间的对比与分析 在群体中恶意节点数f不超过总数1/3的情况下,门限值设为n/3+1,即f+1为门限最小值,可还原出一致性数据,当有f+1个一致的数据即认为是正确数据。同样输入32 B字符串数据,根据不同的预言机节点数量,对Schnorr签名有无加入门限机制的验证时间进行对比,结果如图4所示。 图4 加入门限机制前后的Schnorr签名验证时间对比Figure 4 Comparison of Schnorr signature verification time before and after adding threshold mechanism 从图4可以看出,加入门限机制后签名验证时间相比没有加入门限机制时减少约200 ms,且预言机节点数量越多,验证时间减少得越多。 综上所述,本文提出的基于门限聚合签名的模型同时具有聚合与门限秘密共享能力,在传输数据和签名时,可信任的签名聚合预言机将多个签名聚合为一个签名,与链上智能合约只需要交互一次,而不需要多个预言机与链上智能合约依次交互,大大降低了将多个签名和数据上链后区块链的存储空间,且只需消耗一次gas值。相比于未聚合到一个签名聚合预言机的模型,所提模型既降低了区块链上的存储空间又节省大量的gas成本。 本文提出一种基于门限聚合签名的区块链预言机数据传输模型,将数据和签名聚合到可信任的签名聚合预言机上进行上链,与链上智能合约进行单次交互,减少了链上数据的存储空间;在Schnorr聚合签名中设置门限值,提高签名验证的时间效率;利用多个预言机来收集外部数据信息,通过积分制选举出可信任的预言机进行签名聚合,防止恶意预言机发送错误信息。实验结果表明,使用Schnorr门限聚合签名比BLS聚合签名和未加入门限机制的Schnorr聚合签名验证消耗的时间少,效率更高;相比未聚合的多个预言机数据传输方案,降低了区块链上的存储成本,减少了链上智能合约与多个链下预言机的交互次数,消耗更少的gas值。但是,本模型中单一数据节点的可信任度还有待加强。在接下来的工作中,将研究如何增强预言机间的信任度和提高聚合签名者对作恶预言机的辨识度。1.2 门限秘密共享
1.3 预言机
2 区块链预言机数据传输模型

2.1 Schnorr门限聚合签名


2.2 基于门限聚合签名的预言机数据传输模型


3 实验结果与分析
3.1 理论分析
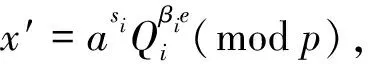



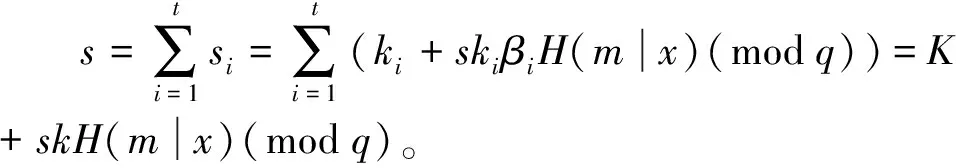
3.2 实验分析

4 结语
