基于鸟群搜索行为和余弦变异的改进白鲨优化算法
2023-05-13张超
张超,杨 忆
(1.宿州职业技术学院计算机信息系,安徽 宿州 234000;2.淮北师范大学计算机科学与技术学院,安徽 淮北 235000)
优化是为一组决策变量寻找最佳组合以解决特定问题的过程[1]。现实世界很多复杂的科学和工程问题本质上是困难的优化问题。他们的目标函数大多是不可微、不连续、非线性和非凸的,涉及许多决策变量并受到各种约束的束缚。基于梯度的传统优化技术,如牛顿法、序列二次规划法等很难为其找到高质量的解[2]。元启发式算法不依赖于问题的梯度信息,其一般优化框架是从一组随机解开始,由多个智能体按照特定元启发式算子协同求解问题[3]。元启发式算法已经成为求解现实世界复杂优化问题的流行方法。
目前,元启发式算法中遗传算法[4](genetic algorithm,GA)、粒子群优化(particle swarm optimizer,PSO)算法[5]、蚁群优化(ant colony optimization,ACO)算法[6]等经典算法被广泛利用。近几年,一些新的元启发式算法涌现出来,如正弦余弦算法(sine cosine algorithm,SCA)[7]、冠状病毒群体免疫优化(coronavirus herd immunity optimizer,CHIO)算法[8]、鲸鱼优化算法[9](whale optimization algorithm,WOA)、蜜獾算法[10](honey badger algorithm,HBA)、野马优化(wild horse optimizer,WHO)算法[11]等。这些算法帮助解决了图像处理[12]、无线传感器网络优化[13]、路径规划[14]、流水车间调度[15]等现实生活领域的诸多问题。
由于元启发式算法的随机性和搜索空间的未知性,这类算法存在缺陷:1)在搜索中无法精确控制种群的多样性;2)算法易早熟收敛,陷入局部极值;3)无法适应于求解所有现实问题。这些缺陷成为新算法提出和对现有算法改进研究的天然动机。克服了缺陷的算法可提高解决现实生活中特定问题的效率。
白鲨优化(white shake optimizer,WSO)算法是Braik 等[1]在2022 年提出的一种新型的元启发式算法,其灵感源自白鲨在深海中利用自己非凡的嗅觉、听觉和视觉系统进行捕猎的行为。他们通过对白鲨捕猎时几个典型行为的数学建模,仿生设计了WSO 算法。然而,与大多数基于种群的算法一样,WSO 算法在处理高维优化问题时亦存在容易早熟收敛、收敛精度低等问题。
为提高WSO 算法在处理高维优化问题的收敛精度,本文提出一种改进的白鲨优化(improved white shake optimizer,IWSO)算法。IWSO 算法使用3 种改进策略:1)引入Sinusoidal 混沌映射(Sinusoidal map)初始化策略,以提高初始解的多样性,使其尽可能地覆盖更多的潜在解空间,从而提高算法收敛速度;2)引入鸟群搜索行为,对白鲨个体的速度更新公式进行改进,赋予白鲨游动速度自适应动态惯性权重,以提高算法的收敛速度;3)在WSO 开发阶段,引入精英白鲨余弦变异策略,以加快算法向最优解进化,以提高收敛精度。为了验证IWSO 算法的性能,本文选取23 个著名基准函数和8 个CEC2014 测试函数做对比分析实验。其结果表明,IWSO 算法优于对比算法,具有良好的寻优性能。
1 白鲨优化(WSO)算法
大白鲨拥有非凡的视觉、嗅觉、听觉和敏感的电磁场感受力,能很好地感知来自环境的各种复杂信息[1],如图1 所示。图1 展示了白鲨各感官系统在搜寻猎物时能够侦察的范围。白鲨利用它们追踪和狩猎。白鲨优化算法主要是以白鲨的3 种典型行为进行数学建模仿生设计的。

图1 白鲨及其感官系统[1]Fig.1 White shark and its sensory system[1]
1.1 朝向猎物移动的速度
大白鲨利用听觉、视觉和嗅觉等非凡感官跟踪猎物。大白鲨根据它在猎物移动时听到的波浪声音感知到猎物位置后,以波浪式向猎物游动,游动速度使用式(1)模拟计算。
式(2)—(5)中:n代表白鲨种群规模;rand(1,n)表示在[0,1]范围内,产生n个服从均匀分布的随机数;k和K分别表示当前和最大迭代次数;pmin和pmax表示白鲨实现良好运动的最小和最大速度,一般取值为0.5 和1.5;τ表示加速度系数,一般取值为4.125。
1.2 朝向最优猎物移动
当白鲨听到猎物移动引起的波浪声或闻到猎物的气味时,会向其移动。某些情况下,当白鲨到达猎物原始位置时,猎物已经离开,这时白鲨会进行搜索:1)根据猎物的气味在当前区域进行局部探索;2)根据猎物制造的波浪声进行全局搜索。这2 种搜索行为使用式(6)模拟计算。
式中sgn 是符号运算符。
式中 ⊕为异或运算。式(7)—(9)主要功能是将搜索空间上下边界值赋予中溢出上下边界的维度。
式中fmin和fmax分别表示波浪式运动的最小和最大频率,一般取值为0.07 和0.75。
式中a0和a1是2 个正常数,用于管理探索和开发行为,一般取值为6.25 和100。
1.3 白鲨的集群行为
白鲨是一种高度社会化的动物。它们喜欢集群捕猎,捕猎时会保持高度合作,朝着最靠近猎物的白鲨移动。WSO 算法使用式(12)模拟群体朝着最佳白鲨移动行为。
式中:a2是一个正常数,控制开发和探索之间的平衡,一般取值为0.000 5。
WSO 算法使用式(15)模拟白鲨集群行为,白鲨个体根据到达最佳位置的白鲨的位置更新自己的位置,该位置非常接近猎物。
2 改进的白鲨优化(IWSO)算法
WSO 算法在低维函数上具有良好的寻优性能,但在高维函数上收敛精度较低,特别在问题维度大于100 维以上时,算法易陷入局部极值,早熟收敛。为此,本文使用3 种策略进行改进,以提高WSO 算法处理高维优化问题的能力。
2.1 Sinusoidal 混沌映射初始化策略
由于初始解会对元启发式算法的最终寻优结果产生较大影响。WSO 算法的初始种群采用随机化方式生成,易导致初始解在搜索域内分布不均,缺乏多样性。为此,引入Sinusoidal 混沌映射初始化种群,利用混沌系统的非线性、随机性和遍历性特点,提高初始种群的多样性和在解空间的分布性,从而提高算法的寻优性能。Sinusoidal 混沌映射的数学表达式为
其中,x∈[0,1],本文a=2.3,x0=0.7。其300 次迭代映射产生的混沌序列值分布如图2 所示。由图2可见,混沌值在[0,1]之间分布均匀,使用其取代WSO 算法的伪随机初始值,能够有效提高初始种群的分布性。

图2 Sinusoidal 混沌映射分布图Fig.2 Distribution diagram of Sinusoidal chaos map
2.2 鸟群搜索行为的速度更新策略
白鲨向猎物游动的速度使用式(1)计算,其对WSO 算法至关重要。在WSO 算法全局搜索阶段主要依赖速度进行位置更新计算。但式(1)使用收缩因子μ对速度更新规则进行整体缩放。μ的值取决于式(5)中加速度系数τ,根据文献[1]的大量数值实验后推荐的τ取值,μ实际值为0.703 46,是一个常数。对速度恒定的缩放,易使白鲨种群失去活性,导致算法在全局搜索时陷入极值,收敛停滞。
为了改进WSO 算法,本文首先删除式(1)中μ缩放因子,并受粒子群优化算法鸟群觅食行为启发,将鸟群飞行速度的惯性权重思想引入式(1)中。改进后的速度更新策略使用式(17)计算。
式中:g是惯性权重参数,由式(18)计算;其他参数及取值和式(1)保持一致。
其中,gmax和gmin是惯性权重上下界,本文中gmax=0.9,gmin=0.2。随着迭代进程,g动态递减。在迭代前期g取较大值,有利于白鲨种群在尽可能大的空间进行全局搜索,找到更多的潜在最优解。在迭代过程中逐渐变小的g,可使得白鲨种群具备精细的局部开发能力,有利于在已找到的潜在最佳解中勘探到更好的最优解。
2.3 精英白鲨余弦变异策略
每代最优白鲨是种群中的精英,离猎物最近,在它的附近邻域小空间内进行精细化开发,能够极大提升找到最佳解的概率,提高收敛精度。为此,本文在WSO 算法开发阶段,引入精英白鲨余弦变异策略,利用余弦函数周期性振荡特征,驱动算法在精英白鲨附近的小邻域内进行勘探。随着算法的运行,精英白鲨更接近于猎物,开发的邻域范围应逐渐收缩,因此,在本文中为余弦函数设计自适应动态递减的振幅。该过程使用式(19)模拟计算。
式中:B是cos(α)的振幅,由式(20)计算;α∈[0,2π],是随机数。em 为余弦变异控制参数,一般取0.2。rand 小于0.2 时进行精英白鲨余弦变异,反之,仍使用WSO 算法原开发策略。
其中,γ为形状控制系数,B的值随迭代次数非线性递减。图3 是不同γ值的B×cos(α)形状对比图,本文γ=100。从图3 可见,在迭代开始,IWSO 算法在精英白鲨稍大邻域内进行搜索,随着迭代进行,在精英白鲨微小邻域内进行开发,以此提高算法收敛速度和精度。
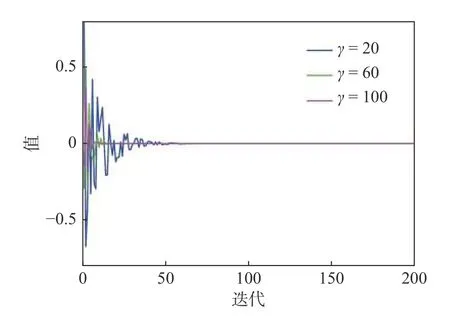
图3 不同γ 值的B×cos(α)形状对比图Fig.3 Shape comparison of B×cos(α) for different values of γ
2.4 IWSO 算法
综上,在Sinusoidal 混沌映射、动态惯性权重的鸟群搜索行为和精英白鲨余弦变异策略的有效集成,成为IWSO 算法。图4 示出改进后的白鲨优化算法的伪代码。

图4 IWSO 算法的伪代码Fig.4 Pseudo-code of IWSO algorithm
3 仿真实验
3.1 实验设计
为充分验证IWSO 算法的寻优性能,仿真实验在2 类领域内普遍接受并能够客观评估元启发式算法性能的函数上进行。一是著名的23 个基准函数,函数详情可参阅文献[8-10]。二是CEC2014中8 个复合函数,函数详情可参阅文献[16]。算法评价指标为寻优结果的最好值、最差值、平均值和标准差。
本文选择近年新兴的5 种算法做对比实验。5种算法分别是:SCA[7]、CHIO算法[8]、WOA[9]、HBA[10]和WHO 算法[11]。为保障算法比较的公平性,所有算法的种群规模设为30,最大迭代次数设为500。IWSO 算法参数使用第2 章已给出的值。对比算法的参数均使用对应文献推荐的设置,以保障其寻优性能最佳。
3.2 在23 个函数上的实验结果和分析
23 个函数分类情况如下:单峰函数,f1~f7;多峰函数,f8~f13;固定维度多峰函数,f14~f23。将f1~f13函数的维度设为30。
3.2.1 单峰函数实验结果
表1 为算法的对比实验结果。由表1 可知,IWSO 算法在f1~f4上每次皆能找到理论最优值,而相应的对比算法均不能。f5被称为“香蕉”函数,一般的元启发式算法在其上表现较差,而IWSO 算法最优值可达1.555 3×10-3级别,平均值亦优于对比算法,表现出优越寻优性能。在f6上:IWSO 算法优于WSO 算法、CHIO 算法、WOA 和SCA;最好值不如HBA 和WHO 算法,但最差值、平均值和标准差均优于它们。在f7上,IWSO 算法在4 个评价指标上亦均优于其他算法。因此,IWSO 算法在单峰函数上的寻优能力整体优于所有对比算法。

表1 单峰函数上的对比实验结果Tab.1 Comparative experimental results on unimodal functions
3.2.2 多峰函数实验结果
表2 为算法在多峰函数上的对比实验结果。由表2 可知,在f8上,IWSO 算法能收敛到理论最优值,其他对比算法均不能,且IWSO 算法的均值和最差值好于所有对比算法。在f9和f11上,IWSO 算法和HBA 每次均能找到理论最优值,整体略优于WHO 算法,大幅优于WSO 算法、CHIO 算法、WOA、SCA。在f10上:IWSO 算法、WOA、HBA 和WHO 算法最好值一样,但从最差值、均值和标准差指标看,IWSO 算法更稳定,鲁棒性优于它们;WSO 算法、CHIO 算法和SCA 表现较差。f12和f13函数较复杂,最优值很难找到,但IWSO 算法整体上优于所有对比算法。综上所述,IWSO 算法在多峰函数上具有良好的收敛精度和鲁棒性。
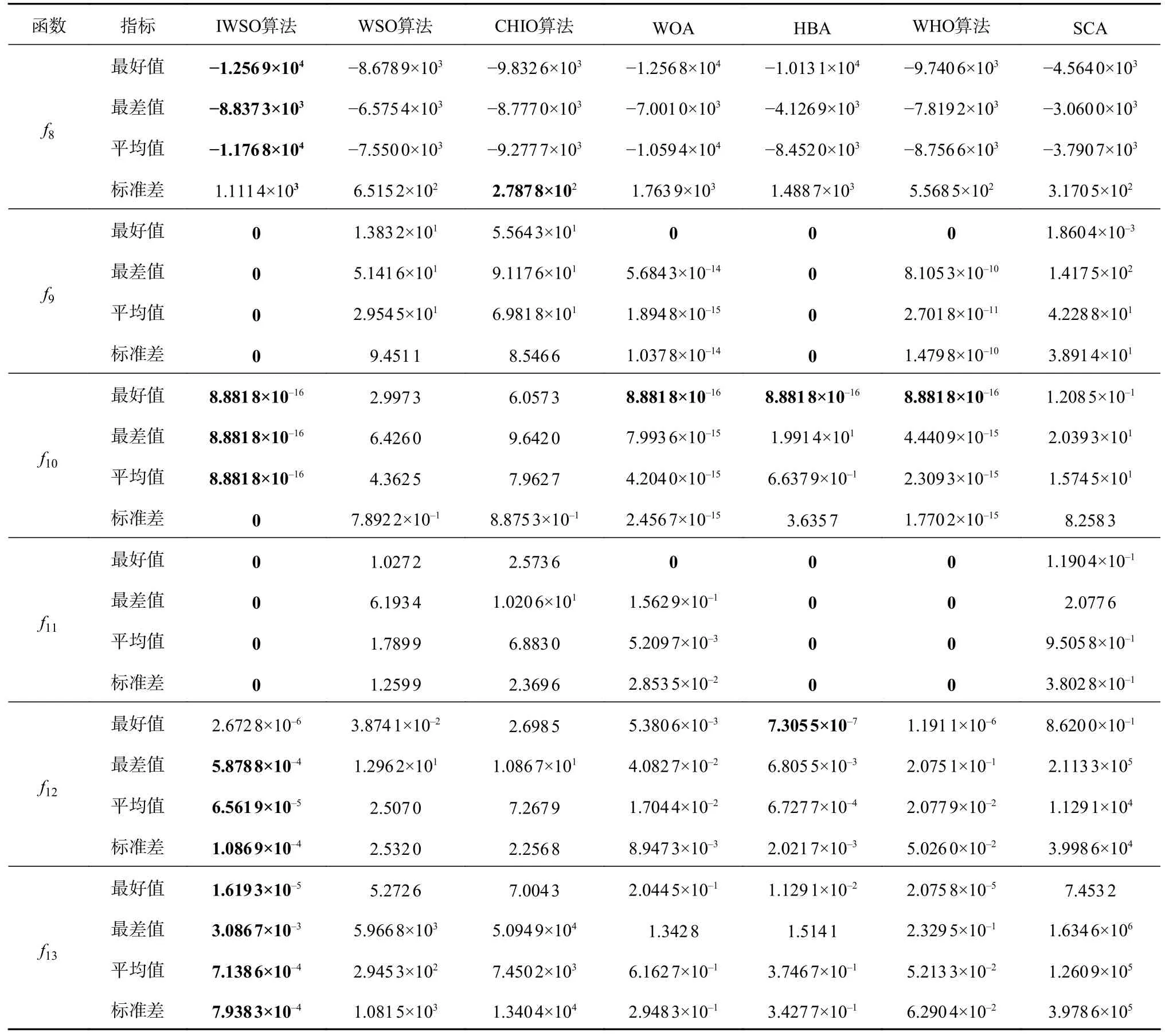
表2 多峰函数上的对比实验结果Tab.2 Comparative experimental results on multimodal functions
3.2.3 固定维度多峰函数实验结果
表3 为算法在固定维度多峰函数上的对比实验结果。从找到理论最优值维度分析:IWSO 算法、WSO 算法、HBA 和WHO 算法在所有10 个函数上都能找到理论最优值;WOA 为5个,CHIO 算法为3个,SCA 为2个,表现相对较差。从算法的稳定性维度分析:除了f14,从均值和标准差看,IWSO 算法表现出稳健的鲁棒性,整体好于对比算法。特别在f15、f21~f23上,IWSO 算法每次均能收敛到理论最优值,表现出优越的鲁棒性,而对比算法均易陷入局部极值,鲁棒性欠佳。因此,IWSO 算法提升了WSO 算法在固定维度多峰函数上寻优的稳定性,整体性能优于其他对比算法。
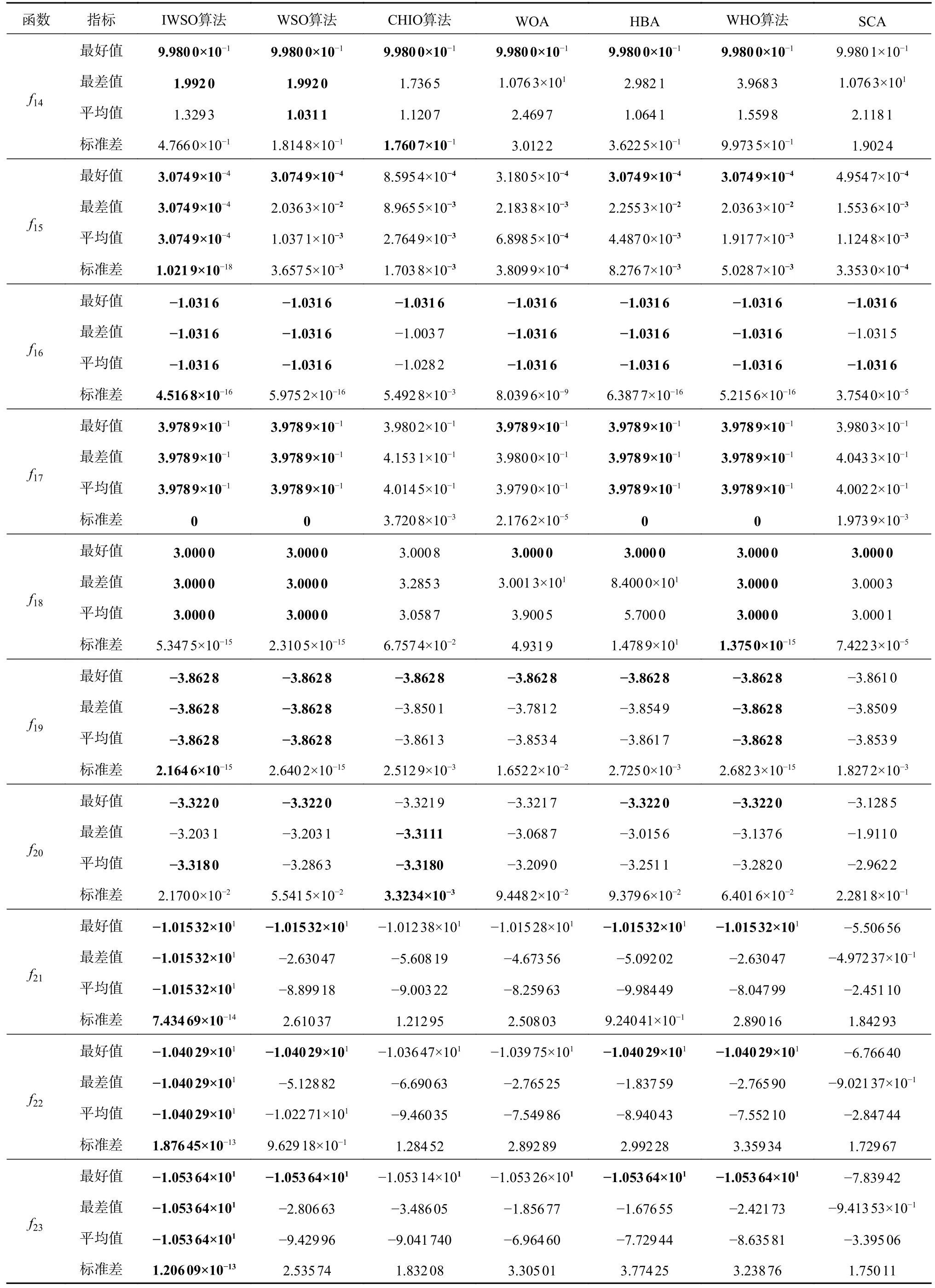
表3 固定维度多峰函数上的对比实验结果Tab.3 Comparison experimental results on fixed dimensional multimodal functions
综上所述,IWSO 算法在3 种不同类型的函数上均表现出了优越的寻优性能,在收敛精度和稳定性上较对比算法大幅提升,说明本文所提出的改进策略是可行和有效的。
3.2.4 收敛性分析
除了收敛精度和稳定性外,衡量一个元启发式算法性能优劣的重要指标是收敛速度。收敛速度代表达到问题预设精度所耗费的迭代周期,在一定程度上反映了算法获得最佳解时所花费时间的优劣。图5 为各算法在部分函数上的收敛曲线对比图。横坐标代表迭代次数,纵坐标代表到目前为止获得的最佳解(做10 为底的对数处理)。
从图5 可见,IWSO 算法的收敛曲线整体呈起伏前进形态,说明算法能够有效跳出局部极值,不断向最佳解收敛。在f1~f4上,IWSO 算法在100 次迭代左右即能收敛到函数的最优值0,对比算法均不能。在f9和f11上,IWSO 算法找到最优值0 仅需几步迭代,较对比算法中表现较好的WOA、HBA、WHO 算法大幅提高。综上说明所提Sinusoidal 混沌映射、动态惯性权重的鸟群搜索行为和精英白鲨余弦变异策略的有效集成,可提高IWSO 算法的收敛速度和精度。

图5 收敛曲线对比图Fig.5 Comparison of convergence curves
3.3 在CEC2014 复合函数上的实验结果和分析
为了进一步验证IWSO 算法在更复杂函数上的寻优性能,本文做IWOS 算法和6 种对比算法在CEC2014 中8 个复杂复合函数上的实验。以平均值、标准差作为评价指标。对实验结果做p=5%显著性水平下的Wilcoxon 秩和检验,以说明实验真实性,以决策算法的性能优劣,实验结果如表4 所示。CEC2014 复合函数较复杂,理论最优值很难获得。从Wilcoxon 秩和检验结果看:IWSO算法在8 个函数上均优于WSO 算法、CHIO 算法、WHO 算法和SCA;IWSO 算法在6 个函数上优于WOA,在2 个函数上相当;IWSO 算法在6 个函数上优于HBA,在f26上相当,在f27上略逊。特别地,在f30、f31上,IWSO 算法的收敛精度较对比算法提升4~6 个数量级。综上,进一步验证了所提3 种策略的有效性。

表4 CEC2014 复合函数上的对比实验结果Tab.4 Comparison experimental results on the CEC2014 composite functions
4 IWSO 在更高维度上的寻优性能
限于篇幅,本文选择f1~f4这4 个函数做维度为300 和1 000 维的实验,以充分展示IWSO 算法在更高维度时的优越性能。对比实验主要在IWSO 算法和基本WSO 算法之间进行,种群规模和最大迭代次数仍设为30 和500,独立进行30 次实验,实验结果如表5 所示。表5 的平均值和标准差指标清晰地表明:IWSO 算法在300 维和1 000维时每次都能收敛到函数的最优值0,不受维度变大的影响;基本WSO 算法在300 和1 000 维上收敛结果变得更差。这进一步说明,IWSO 算法充分解决了WSO 算法处理高维函数时性能较差的不足,达到了算法改进的目的。
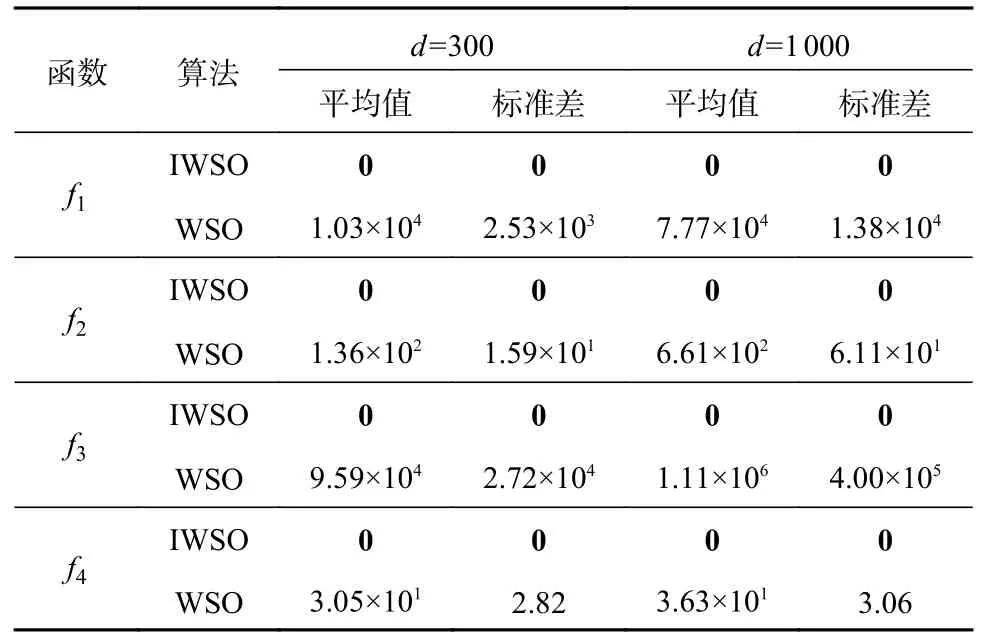
表5 在更高维度上的对比实验结果Tab.5 Comparison experimental results in higher dimensions
5 结论
针对白鲨优化(WSO)算法在处理高维函数时存在早熟收敛,精度较差的不足,提出了一种改进的白鲨优化(IWSO)算法。IWSO 算法集成了Sinusoidal 混沌映射初始化策略、基于鸟群搜索行为的速度更新策略和精英白鲨余弦变异策略。首先,在23 个基准函数和CEC2014 中8 个复合函数上进行了对比实验,实验结果表明,IWSO 算法在收敛精度、速度及其鲁棒性上整体优于WSO 算法、CHIO 算法、WOA、HBA、WHO 算法和SCA。其次,在300 和1 000 维度上做更高维度性能分析实验,结果表明,IWSO 算法均能收敛到函数的理论最优值,充分解决了WSO 算法处理高维函数时性能较差的不足。大量实验结果表明,3 种策略的有效集成提高了初始解的多样性及在解空间的分布,加快了白鲨向猎物游动的速度,有效维持了探索和开发之间的微平衡,进而达到了提升算法性能的目的。白鲨优化(WSO)算法是2022 年新提出的元启发式算法,相关研究和应用尚处于起步阶段,下一步的重点工作,将研究使用IWSO 算法解决现实世界的实际工程优化问题。
